15.6: Tamaños de muestra desiguales
- Page ID
- 152305
Objetivos de aprendizaje
- Indicar por qué la desigualdad\(n\) puede ser un problema
- Definir confusión
- Calcular medias ponderadas y no ponderadas
- Distinguir entre sumas de cuadrados Tipo I y Tipo III
- Describir por qué la causa de los tamaños de muestra desiguales marca la diferencia en la interpretación
El problema de la confusión
Ya sea por diseño, accidente o necesidad, el número de sujetos en cada una de las condiciones en un experimento puede no ser igual. Por ejemplo, los tamaños de muestra para el estudio de caso “Sesgo Against Associates of the Obese” se muestran en la Tabla\(\PageIndex{1}\). Aunque los tamaños de muestra fueron aproximadamente iguales, la condición “Conocido Típico” tuvo la mayor cantidad de sujetos. Dado que\(n\) se utiliza para referirse al tamaño de muestra de un grupo individual, los diseños con tamaños de muestra desiguales a veces se denominan diseños con desiguales\(n\).
| Peso acompañante | |||
|---|---|---|---|
| Obesos | Típico | ||
| Relación | Novia | 40 | 42 |
| Conocido | 40 | 54 | |
Consideramos un diseño absurdo para ilustrar el principal problema causado por la desigualdad\(n\). Supongamos que un experimentador estaba interesado en los efectos de la dieta y el ejercicio sobre el colesterol. Los tamaños de muestra se muestran en la Tabla\(\PageIndex{2}\).
| Ejercicio | |||
|---|---|---|---|
| Moderado | Ninguno | ||
| Dieta | Bajo en Grasa | 5 | 0 |
| Alta Grasa | 0 | 5 | |
Lo que hace absurdo este ejemplo es que no hay sujetos ni en la condición “Bajo en grasa sin ejercicio” ni en la condición de “Ejercicio moderado con alto contenido de grasa”. Los datos hipotéticos que muestran cambio en el colesterol se muestran en la Tabla\(\PageIndex{3}\).
| Ejercicio | ||||
|---|---|---|---|---|
| Moderado | Ninguno | Media | ||
| Dieta | Bajo en Grasa | -20 | -25 | |
| -25 | ||||
| -30 | ||||
| -35 | ||||
| -15 | ||||
| Alta Grasa | -20 | -5 | ||
| 6 | ||||
| -10 | ||||
| -6 | ||||
| 5 | ||||
| Media | -25 | -5 | -15 | |
La última columna muestra el cambio medio en el colesterol para las dos condiciones de la Dieta, mientras que la última fila muestra el cambio promedio en el colesterol para las dos Condiciones de ejercicio. El valor de\(-15\) en la celda inferior derecha de la tabla es la media de todos los sujetos.
Vemos de la última columna que quienes estaban en la dieta baja en grasas bajaron su colesterol un promedio de\(25\) unidades, mientras que los de la dieta alta en grasas bajaron el suyo solo en un promedio de\(5\) unidades. Sin embargo, no hay manera de saber si la diferencia se debe a la dieta o al ejercicio, ya que cada sujeto en la condición baja en grasa estaba en la condición de ejercicio moderado y cada sujeto en la condición alta en grasa estaba en la condición de no ejercicio. Por lo tanto, la Dieta y el Ejercicio están completamente confundidos. El problema con la desigualdad\(n\) es que causa confusión.
Medias ponderadas y no ponderadas
La diferencia entre medias ponderadas y no ponderadas es una diferencia crítica para entender cómo lidiar con la confusión resultante de la desigualdad\(n\).
Las medias ponderadas y no ponderadas se explicarán utilizando los datos que se muestran en la Tabla\(\PageIndex{4}\). Aquí, la Dieta y el Ejercicio se confunden debido a\(80\%\) los sujetos en la condición baja en grasa ejercida en comparación\(20\%\) con aquellos en la condición alta en grasas. Sin embargo, no hay confusión completa como lo hubo con los datos de la Tabla\(\PageIndex{3}\).
La media ponderada para “Bajo en Grasa” se computa como la media de la media “Bajo en Grasa Moderado-Ejercicio” y la media “Baja en Grasa Sin Ejercicio”, ponderada de acuerdo con el tamaño de la muestra. Para calcular una media ponderada, se multiplica cada media por su tamaño de muestra y se divide por\(N\), el número total de observaciones. Dado que hay cuatro sujetos en la condición “Bajo en grasa moderado-ejercicio” y un sujeto en la condición “Bajo en grasa sin ejercicio”, las medias se ponderan por factores de\(4\) y\(1\) como se muestra a continuación, donde\(M_W\) está la media ponderada.
\[M_W=\frac{(4)(-27.5)+(1)(-20)}{5}=-26\]
La media ponderada para la condición baja en grasa es también la media de las cinco puntuaciones en esta condición. Por lo tanto, si ignoras el factor “Ejercicio”, estás computando implícitamente las medias ponderadas.
La media no ponderada para la condición baja en grasa (\(M_U\)) es simplemente la media de las dos medias.
\[M_U=\frac{-27.5-20}{2}=-23.75\]
| Ejercicio | |||||
|---|---|---|---|---|---|
| Moderado | Ninguno | Media ponderada | Media no ponderada | ||
| Dieta | Bajo en Grasa | -20 | -20 | -26 | -23.750 |
| -25 | |||||
| -30 | |||||
| -35 | |||||
| M=-27.5 | M=-20.0 | ||||
| Alta Grasa | -15 | 6 | -4 | -8.125 | |
| -6 | |||||
| 5 | |||||
| -10 | |||||
| M=-15.0 | M=-1.25 | ||||
| Media ponderada | -25 | -5 | |||
| Media no ponderada | -21.25 | -10.625 | |||
Una forma de evaluar el efecto principal de la Dieta es comparar la media ponderada para la dieta baja en grasas (\(-26\)) con la media ponderada para la dieta alta en grasas (\(-4\)). Esta diferencia de\(-22\) se llama “el efecto de la dieta ignorando el ejercicio” y es engañosa ya que la mayoría de los sujetos bajos en grasa hicieron ejercicio y la mayoría de los sujetos altos en grasas no lo hicieron. Sin embargo, la diferencia entre las medias no ponderadas de\(-15.625\) (\((-23.750)-(-8.125)\)) no se ve afectada por esta confusión y, por lo tanto, es una mejor medida del efecto principal. En resumen, las medias ponderadas ignoran los efectos de otras variables (ejercicio en este ejemplo) y resultan en confusión; las medias no ponderadas controlan el efecto de otras variables y por lo tanto eliminan la confusión.
Los programas de análisis estadístico utilizan diferentes términos para medios que se computan controlando para otros efectos. SPSS las llama medias marginales estimadas, mientras que SAS y SAS JMP las llaman medias de mínimos cuadrados.
Tipos de Sumas de Cuadrados
El apartado sobre ANOVA Multi-Factor estableció que cuando hay tamaños de muestra desiguales, la suma de cuadrados totales no es igual a la suma de las sumas de cuadrados para todas las demás fuentes de variación. Esto se debe a que las sumas confundidas de cuadrados no se reparten a ninguna fuente de variación. Para los datos en Tabla\(\PageIndex{4}\), la suma de cuadrados para Dieta es\(390.625\), la suma de cuadrados para Ejercicio es\(180.625\), y la suma de cuadrados confundidos entre estos dos factores es\(819.375\) (el cálculo de este valor está fuera del alcance de este texto introductorio). En la Tabla de Resumen de ANOVA que se muestra en la Tabla\(\PageIndex{5}\), esta gran porción de las sumas de cuadrados no se reparte a ninguna fuente de variación y representa las sumas de cuadrados “faltantes”. Es decir, si sumas las sumas de cuadrados para Dieta\(D \times E\), Ejercicio y Error, obtienes\(902.625\). Si agregas la suma confundida de cuadrados de\(819.375\) a este valor, obtienes la suma total de cuadrados de\(1722.000\). Cuando las sumas confundidas de cuadrados no se reparten a ninguna fuente de variación, las sumas de cuadrados se denominan sumas de cuadrados Tipo III. Las sumas de cuadrados de tipo III son, con mucho, las más comunes y si las sumas de cuadrados no se etiquetan de otra manera, se puede suponer con seguridad que son de Tipo III.
| Fuente | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Dieta | 1 | 390.625 | 390.625 | 7.42 | 0.034 |
| Ejercicio | 1 | 180.625 | 180.625 | 3.43 | 0.113 |
| D x E | 1 | 15.625 | 15.625 | 0.30 | 0.605 |
| Error | 6 | 315.750 | 52.625 | ||
| Total | 9 | 1722.000 |
Cuando todas las sumas confundidas de cuadrados se reparten a fuentes de variación, las sumas de cuadrados se denominan sumas de cuadrados Tipo I. El orden en que se reparten las sumas confundidas de cuadrados viene determinado por el orden en que se listan los efectos. El primer efecto obtiene cualquier suma de cuadrados confundida entre éste y cualquiera de los otros efectos. El segundo obtiene las sumas de cuadrados confundidos entre éste y los efectos posteriores, pero no confundidos con el primer efecto, etc. Las sumas de cuadrados Tipo I se muestran en la Tabla\(\PageIndex{6}\). Como puede ver, con sumas de cuadrados Tipo I, la suma de todas las sumas de cuadrados es la suma total de cuadrados.
| Fuente | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| Dieta | 1 | 1210.000 | 1210.000 | 22.99 | 0.003 |
| Ejercicio | 1 | 180.625 | 180.625 | 3.43 | 0.113 |
| D x E | 1 | 15.625 | 15.625 | 0.30 | 0.605 |
| Error | 6 | 315.750 | 52.625 | ||
| Total | 9 | 1722.000 |
En las sumas de cuadrados Tipo II, las sumas de cuadrados confundidas entre los efectos principales no se reparten a ninguna fuente de variación, mientras que las sumas de cuadrados confundidas entre efectos principales e interacciones se reparten a los efectos principales. En nuestro ejemplo, no hay confusión entre la\(D \times E\) interacción y ninguno de los efectos principales. Por lo tanto, las sumas de cuadrados Tipo II son iguales a las sumas de cuadrados Tipo III.
Qué Tipo de Sumas de Cuadrados Usar (opcional)
Las sumas de cuadrados tipo I permiten que la varianza confundida entre dos efectos principales se distribuya a uno de los efectos principales. A menos que exista un argumento fuerte sobre cómo se debe repartir la varianza confundida (que rara vez es, si alguna vez, el caso), no se recomiendan las sumas de cuadrados de Tipo I.
No hay consenso sobre si se prefieren las sumas de cuadrados Tipo II o Tipo III. Por un lado, si no hay interacción, entonces las sumas de cuadrados Tipo II serán más poderosas por dos razones:
- varianza confundida entre el efecto principal y la interacción se asigna adecuadamente al efecto principal y
- ponderar las medias por tamaños de muestra da mejores estimaciones de los efectos.
Para aprovechar la mayor potencia de las sumas de cuadrados Tipo II, algunos han sugerido que si la interacción no es significativa, entonces se deben usar sumas de cuadrados Tipo II. Maxwell y Delaney (2003) advirtieron que tal enfoque podría resultar en un error Tipo II en la prueba de la interacción. Es decir, podría llevar a la conclusión de que no hay interacción en la población cuando realmente la hay. Esto, a su vez, aumentaría la tasa de error Tipo I para la prueba del efecto principal. En consecuencia, su recomendación general es utilizar sumas de cuadrados Tipo III.
Maxwell y Delaney (2003) reconocieron que algunos investigadores prefieren sumas de cuadrados Tipo II cuando hay fuertes razones teóricas para sospechar una falta de interacción y el valor de p es mucho mayor que el\(α\) nivel típico de\(0.05\). Sin embargo, este argumento para el uso de sumas de cuadrados Tipo II no es del todo convincente. Como han argumentado Tukey (1991) y otros, es dudoso que algún efecto, ya sea un efecto principal o una interacción, esté exactamente\(0\) en la población. Por cierto, Tukey argumentó que el papel de las pruebas de significación es determinar si se puede llegar a una conclusión segura sobre la dirección de un efecto, no simplemente concluir que un efecto no es exactamente\(0\).
Finalmente, si uno asume que no hay interacción, entonces se debe usar un modelo ANOVA sin término de interacción en lugar de sumas de cuadrados Tipo II en un modelo que incluya un término de interacción. (Los modelos sin términos de interacción no están cubiertos en este libro).
Hay situaciones en las que las sumas de cuadrados de Tipo II se justifican aunque exista una fuerte interacción. Este es el caso porque las hipótesis probadas por las sumas de cuadrados Tipo II y Tipo III son diferentes, y la elección de cuál usar debe guiarse por qué hipótesis es de interés. Recordemos que las sumas de los cuadrados de Tipo II pesan las células en función de sus tamaños de muestra mientras que las sumas de cuadrados de Tipo III pesan todas las células Considere la Figura\(\PageIndex{1}\) que muestra datos de un\(A(2) \times B(2)\) diseño hipotético. Los tamaños de muestra se muestran numéricamente y se representan gráficamente por las áreas de los puntos finales.
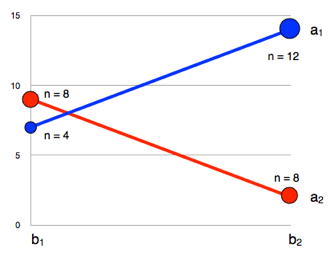
Primero, consideremos la hipótesis para el efecto principal de\(B\) probado por las sumas de cuadrados Tipo III. Las sumas de cuadrados tipo III ponderan las medias por igual y, para estos datos, las medias marginales para\(b_1\) y\(b_2\) son iguales:
Para\(b_1:(b_1a_1 + b_1a_2)/2 = (7 + 9)/2 = 8\)
Para\(b_2:(b_2a_1 + b_2a_2)/2 = (14+2)/2 = 8\)
Por lo tanto, no hay efecto principal de\(B\) cuando se prueban usando sumas de cuadrados de Tipo III. Para las sumas de cuadrados Tipo II, las medias se ponderan por tamaño muestral.
Para\(b_1: (4 \times b_1a_1 + 8 \times b_1a_2)/12 = (4 \times 7 + 8 \times 9)/12 = 8.33\)
Para\(b_2: (12 \times b_2a_1 + 8 \times b_2a_2)/20 = (12 \times 14 + 8 \times 2)/20 = 9.2\)
Dado que la media marginal ponderada para\(b_2\) es mayor que la media marginal ponderada para\(b_1\), existe un efecto principal de\(B\) cuando se prueban usando sumas de cuadrados de Tipo II.
Los análisis Tipo II y Tipo III están probando diferentes hipótesis. Primero, consideremos el caso en el que surgen las diferencias en los tamaños de muestra porque en el muestreo de grupos intactos, los tamaños de células de la muestra reflejan los tamaños de células de la población (al menos aproximadamente). En este caso, tiene sentido ponderar unos medios más que otros y concluir que hay un efecto principal de\(B\). Este es el resultado obtenido con sumas de cuadrados Tipo II. Sin embargo, si las diferencias en el tamaño de la muestra surgieron de la asignación aleatoria, y simplemente sucedieron más observaciones en algunas celdas que en otras, entonces uno querría estimar cuáles habrían sido los efectos principales con tamaños de muestra iguales y, por lo tanto, ponderar las medias por igual. Con las medias ponderadas por igual, no hay efecto principal de\(B\), el resultado obtenido con sumas de cuadrados Tipo III.
Análisis de medias no ponderadas
Las sumas de cuadrados tipo III son pruebas de diferencias en medias no ponderadas. Sin embargo, existe un método alternativo para probar las mismas hipótesis probadas usando sumas de cuadrados Tipo III. Este método, el análisis de medias no ponderadas, es computacionalmente más simple que el método estándar pero es una prueba aproximada en lugar de una prueba exacta. Es, sin embargo, una muy buena aproximación en todos los casos menos extremos. Además, es exactamente lo mismo que la prueba tradicional para efectos con un grado de libertad. El Laboratorio de Análisis utiliza análisis de medias no ponderadas y por lo tanto puede no coincidir con los resultados de otros programas de computadora exactamente cuando hay n desigual y los df son mayores que uno.
Causas de tamaños de muestra desiguales
Ninguno de los métodos para tratar tamaños de muestra desiguales son válidos si el tratamiento experimental es la fuente de los tamaños de muestra desiguales. Imagínese un experimento que busque determinar si realizar públicamente un acto vergonzoso afectaría la ansiedad de uno por hablar en público. En este experimento imaginario, se pide al grupo experimental que revele a un grupo de personas lo más vergonzoso que hayan hecho jamás. Se pide al grupo control que describa lo que tuvieron en su última comida. Se reclutaron 20 sujetos para el experimento y se dividieron aleatoriamente en dos grupos iguales de\(10\), uno para el tratamiento experimental y otro para el testigo. Siguiendo sus descripciones, los sujetos reciben una encuesta de actitud respecto a hablar en público. Esto parece un diseño experimental válido. Sin embargo, de los\(10\) sujetos del grupo experimental, cuatro se retiraron del experimento porque no quisieron describir públicamente una situación embarazosa. Ninguno de los sujetos del grupo control se retiró. Aun cuando el análisis de datos mostrara un efecto significativo, no sería válido concluir que el tratamiento tuvo efecto porque no se puede descartar una explicación alternativa probable; es decir, los sujetos que estaban dispuestos a describir una situación embarazosa diferían de los que no lo estaban. Así, la tasa de deserción diferencial destruyó la asignación aleatoria de sujetos a condiciones, característica crítica del diseño experimental. Ninguna cantidad de ajuste estadístico puede compensar esta falla.
- Maxwell, S. E., & Delaney, H. D. (2003) Diseñando experimentos y analizando datos: una perspectiva de comparación de modelos, segunda edición, Lawrence Erlbaum Associates, Mahwah, Nueva Jersey.
- Tukey, J. W. (1991) La filosofía de las comparaciones múltiples, Ciencia estadística, 6, 110-116.


