15.7: Pruebas suplementarias
- Page ID
- 152324
Objetivos de aprendizaje
- Prueba HSD de Tukey Compute
- Describir una interacción en palabras
- Describir por qué uno podría querer calcular pruebas de efectos simples después de una interacción significativa
La hipótesis nula probada en un ANOVA de un factor es que todas las medias poblacionales son iguales. Declarado de manera más formal,
\[H_0: \mu _1 = \mu _2 = \cdots = \mu _k\]
donde\(H_0\) está la hipótesis nula y\(k\) es el número de condiciones. Cuando se rechaza la hipótesis nula, todo lo que se puede decir es que al menos una media poblacional es diferente de al menos otra media poblacional. Aquí se aplican los métodos para hacer pruebas más específicas descritas Todas las Comparaciones por Pares entre Medias y en Comparaciones Específicas. Tenga en cuenta que estas pruebas son válidas estén o no precedidas de un ANOVA.
Efectos principales
Como se muestra a continuación, los efectos principales significativos en los diseños multifactoriales pueden ser seguidos de la misma manera que los efectos significativos en diseños unidireccionales. El cuadro\(\PageIndex{1}\) muestra los datos de un experimento imaginario con tres niveles de\(\text{Factor A}\) y dos niveles de\(\text{Factor B}\).
| A1 | A2 | A3 | Medias Marginales | |
|---|---|---|---|---|
| B1 | 5 | 9 | 7 | 7.08 |
| 4 | 8 | 9 | ||
| 6 | 7 | 9 | ||
| 5 | 8 | 8 | ||
| Media = 5 | Media = 8 | Media = 8.25 | ||
| B2 | 4 | 8 | 8 | 6.50 |
| 3 | 6 | 9 | ||
| 6 | 8 | 7 | ||
| 8 | 5 | 6 | ||
| Media = 5.25 | Media = 6.75 | Media = 7.50 | ||
| Medias Marginales | 5.125 | 7.375 | 7.875 | 6.79 |
En el cuadro se\(\PageIndex{2}\) muestra la Tabla de Resumen ANOVA para estos datos. El efecto principal significativo de\(A\) indica que, en la población, al menos una de las medias marginales para\(A\) es diferente de al menos una de las otras.
| Fuente | df | SSQ | MS | F | p |
|---|---|---|---|---|---|
| A | 2 | 34.333 | 17.167 | 9.29 | 0.0017 |
| B | 1 | 2.042 | 2.042 | 1.10 | 0.3070 |
| A x B | 2 | 2.333 | 1.167 | 0.63 | 0.5431 |
| Error | 18 | 33.250 | 1.847 | ||
| Total | 23 | 71.958 |
La prueba de Tukey HSD se puede utilizar para probar todas las comparaciones por pares entre medias en un ANOVA de un factor, así como comparaciones entre medias marginales en un ANOVA multifactor. A continuación se muestra la fórmula para el caso de igual tamaño de muestra.
\[Q = \cfrac{M_i-M_j}{\sqrt{\cfrac{MSE}{n}}}\]
donde\(M_i\) y\(M_j\) son medias marginales,\(MSE\) es el error cuadrático medio del ANOVA, y n es el número de puntuaciones en las que se basa cada media. Para este ejemplo,\(MSE = 1.847\) y\(n = 8\) porque hay ocho puntuaciones en cada nivel de\(A\). El valor de probabilidad se puede calcular usando la Calculadora de Rango Estudentizado. Los grados de libertad son iguales a los grados de error de libertad. Para este ejemplo,\(df = 18\). Los resultados de la prueba Tukey HSD se muestran en la Tabla\(\PageIndex{3}\). La media para\(A_1\) es significativamente menor que la media para\(A_2\) y la media para\(A_3\). Los medios para\(A_2\) y no\(A_3\) son significativamente diferentes.
| Comparación | M i - M j | Q | p |
|---|---|---|---|
| A 1 - A 2 | -2.25 | -4.68 | 0.010 |
| A 1 - A 3 | -2.75 | -5.72 | 0.002 |
| A 2 - A 3 | -0.50 | -1.04 | 0.746 |
Las comparaciones específicas entre medias también se llevan a cabo de la misma manera que se muestra en la sección relevante sobre medios de prueba. La fórmula para\(L\) es
\[L = \sum c_i M_i\]
donde\(c_i\) es el coeficiente para la media\(i^{th}\) marginal y\(M_i\) es la media\(i^{th}\) marginal. Por ejemplo, para comparar\(A_1\) con el promedio de\(A_2\) y\(A_3\), los coeficientes serían\(1\),\(-0.5\),\(-0.5\). Por lo tanto,
\[L = (1)(5.125) + (-0.5)(7.375) + (-0.5)(7.875) = -2.5\]
Para calcular\(t\), utilice:
\[\begin{align*} t &= \cfrac{L}{\sqrt{\cfrac{\sum c_{i}^{2}MSE}{n}}}\\ &= -4.25 \end{align*}\]
donde\(MSE\) es el error cuadrático medio del ANOVA y n es el número de puntuaciones en las que se basa cada media marginal (ocho en este ejemplo). Los grados de libertad son los grados de libertad error del ANOVA y es igual a\(18\). Usando la Calculadora en Línea, encontramos que el valor de probabilidad de dos colas es\(0.0005\). Por lo tanto, la diferencia entre\(A_1\) y el promedio de\(A_2\) y\(A_3\) es significativa.
Calculadora de distribución t
Los temas importantes relacionados con las comparaciones múltiples y las comparaciones ortogonales se discuten en la sección Comparaciones Específicas del capítulo Medios de Prueba.
Interacciones
La presencia de una interacción significativa hace que la interpretación de los resultados sea más complicada. Dado que una interacción significa que los efectos simples son diferentes, el efecto principal como la media de los efectos simples no cuenta toda la historia. En esta sección se analiza cómo describir las interacciones, los usos adecuados e inadecuados de las pruebas de efectos simples y cómo probar los componentes de las interacciones.
Describiendo las interacciones
Un primer paso crucial para comprender una interacción significativa es construir una trama de interacción. La figura\(\PageIndex{1}\) muestra una gráfica de interacción a partir de los datos presentados en la sección sobre ANOVA Multi-Factor.
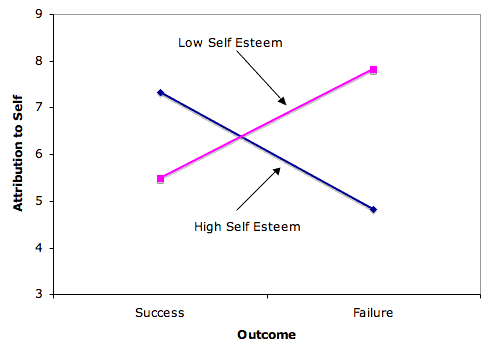
El segundo paso es describir la interacción de una manera clara y comprensible. Esto a menudo se hace describiendo cómo diferían los efectos simples. Dado que esto debe hacerse usando la menor jerga posible, la expresión “efecto simple” no necesita aparecer en la descripción. Un ejemplo es el siguiente:
El efecto del Resultado difería en función de la autoestima del sujeto. La diferencia entre la atribución al autoseguimiento del éxito y la atribución al autoseguimiento del fracaso fue mayor para los sujetos de alta autoestima (diferencia de medias =\(2.50\)) que para los sujetos de baja autoestima (diferencia de medias =\(-2.33\)).
No hay más análisis útiles para comprender la interacción, ya que la interacción significa solo que los efectos simples difieren. La significación de la interacción indica que los efectos simples difieren entre sí, pero no proporciona información sobre si difieren de cero.
Pruebas de Efecto Simple
No es necesario saber si los efectos simples difieren de cero para entender una interacción porque la cuestión de si los efectos simples difieren de cero no tiene nada que ver con la interacción excepto que si ambos son cero no hay interacción. No es raro ver artículos de investigación en los que los autores reportan que analizaron efectos simples para explicar la interacción. Sin embargo, este no es un enfoque válido ya que una interacción no depende del análisis de los efectos simples.
Sin embargo, hay una razón para probar efectos simples después de una interacción significativa. Dado que una interacción indica que los efectos simples difieren, significa que los efectos principales no son generales. En el ejemplo maquillado, el efecto principal del Resultado no es muy informativo, y el efecto del desenlace debe considerarse por separado para sujetos de alta y baja autoestima.
Como se verá, los efectos simples del Resultado son significativos y en direcciones opuestas: El éxito aumenta significativamente la atribución a uno mismo para sujetos de alta autoestima y disminuye significativamente la atribución a uno mismo para sujetos de baja autoestima. Este es un resultado muy fácil de interpretar.
¿Cuál habría sido la interpretación si ninguno de los dos simples efectos hubiera sido significativo? En la superficie, esto parece imposible: ¿Cómo pueden ambos efectos simples ser cero si difieren entre sí significativamente como lo prueba la interacción? La respuesta es que un efecto simple no significativo no significa que el efecto simple sea cero: la hipótesis nula no debe aceptarse solo porque no es rechazada.
(Ver sección Interpretación de resultados no significativos)
Si ninguno de los dos efectos simples es significativo, la conclusión debería ser que los efectos simples difieren, y que al menos uno de ellos no es cero. Sin embargo, no se debe sacar ninguna conclusión sobre qué efecto simple (s) es/no son cero.
Otro error que se puede cometer al aceptar erróneamente la hipótesis nula es concluir que dos efectos simples son diferentes porque uno es significativo y el otro no. Considere los resultados de un experimento imaginario en el que el investigador planteó la hipótesis de que las personas adictas mostrarían un aumento mayor en la actividad cerebral después de algún tratamiento que las personas no adictas. Es decir, el investigador planteó la hipótesis de que el estado de adicción y el tratamiento interactuarían. Los resultados mostrados en la Figura\(\PageIndex{2}\) están muy en línea con la hipótesis. Sin embargo, la prueba de la interacción resultó en un valor de probabilidad de\(0.08\), un valor no lo suficientemente bajo como para ser significativo a\(0.05\) nivel convencional. La conclusión adecuada es que el experimento apoya la hipótesis del investigador, pero no lo suficientemente fuerte como para permitir una conclusión segura.
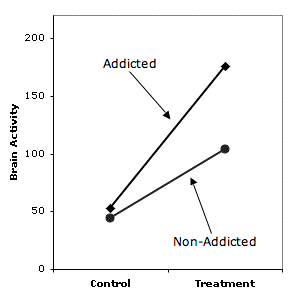
Desafortunadamente, el investigador no estaba satisfecho con una conclusión tan débil y pasó a probar los efectos simples. Resultó que el efecto de Tratamiento fue significativo para el grupo Adictos (\(p = 0.02\)) pero no significativo para el grupo de No Adictos (\(p = 0.09\)). El investigador luego concluyó que dado que existe un efecto de Tratamiento para el grupo Adictos pero no para el grupo No Adictos, se demuestra la hipótesis de un mayor efecto para el primero que para el segundo grupo. Esto es lógica defectuosa, sin embargo, ya que se basa en aceptar la hipótesis nula de que el efecto simple del Tratamiento es cero para el grupo de No Adictos solo porque no es significativo.
Componentes de Interacción (opcional)
La figura\(\PageIndex{3}\) muestra los resultados de un experimento imaginario sobre dieta y pérdida de peso. Se utilizó un grupo control y dos dietas tanto para adolescentes con sobrepeso como para adultos con sobrepeso.
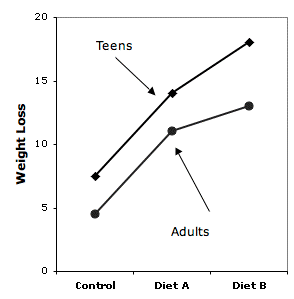
La diferencia entre\(\text{Diet A}\) y la dieta Control fue esencialmente la misma para adolescentes y adultos, mientras que la diferencia entre\(\text{Diet B}\) y\(\text{Diet A}\) fue mucho mayor para los adolescentes que para los adultos. Sobre una porción de la gráfica las líneas son paralelas mientras que sobre otra porción no lo son. Es posible probar estas porciones o componentes de interacciones utilizando el método de comparaciones específicas discutido anteriormente. La prueba de la diferencia entre Adolescentes y Adultos sobre la diferencia entre Dietas\(A\) y se\(B\) pudo probar con los coeficientes mostrados en la Tabla\(\PageIndex{4}\). Naturalmente, las mismas consideraciones respecto a comparaciones múltiples y comparaciones ortogonales que se aplican a otras comparaciones entre medias también se aplican a comparaciones que involucran componentes de interacciones.
| Grupo de edad | Dieta | Coeficiente |
|---|---|---|
| Adolescente | Control | 0 |
| Adolescente | A | 1 |
| Adolescente | B | -1 |
| Adulto | Control | 0 |
| Adulto | A | -1 |
| Adulto | B | 1 |


