Saltar al contenido principal
LibreTexts Español

17.7: Chi Cuadrado (Ejercicios)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    152387

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Preguntas Generales

    Q1

    ¿Cuál de las dos distribuciones de Chi Square que se muestran a continuación (\(A\)o\(B\)) tiene los mayores grados de libertad? ¿Cómo lo sabes? (sección pertinente)

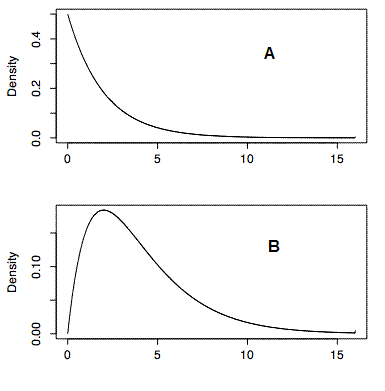
    two_dists.gif

    Q2

    Doce sujetos recibieron cada uno dos sabores de helado al gusto y luego se les preguntó si les gustaban. A dos de los temas les gustó el primer sabor y a nueve de ellos le gustó el segundo sabor. ¿Es válido utilizar la prueba de Chi Cuadrado para determinar si esta diferencia en proporciones es significativa? ¿Por qué o por qué no? (sección pertinente)

    Q3

    Se sospecha que un dado está sesgado. Se enrolla\(25\) tiempos con el siguiente resultado:

    Resultado
    Frecuencia
    1
    9
    2
    4
    3
    1
    4
    8
    5
    3
    6
    0

    Realizar una prueba de significancia para ver si el dado está sesgado.

    1. ¿Qué valor de Chi Square obtienes y cuántos grados de libertad tiene?
    2. ¿Cuál es el\(p\) valor? (sección pertinente)

    Q4

    Un experimento reciente investigó la relación entre el tabaquismo y la incontinencia urinaria. De los\(322\) sujetos en el estudio que eran incontinente,\(113\) eran fumadores,\(51\) eran ex fumadores y nunca\(158\) habían fumado. De los sujetos\(284\) control que no eran incontinente,\(68\) eran fumadores,\(23\) eran exfumadores y nunca\(193\) habían fumado.

    1. Crear una tabla que muestre estos datos.
    2. ¿Cuál es la frecuencia esperada en cada celda?
    3. Realizar una prueba de significancia para ver si existe una relación entre el tabaquismo y la incontinencia. ¿Qué valor de Chi Square obtienes? ¿Qué\(p\) valor obtienes?
    4. ¿Qué concluyes? (sección pertinente)

    Q5

    En un mitin de pep escolar, un grupo de estudiantes de segundo año organizó una rifa gratuita por premios. Afirman que pusieron en la canasta los nombres de todos los alumnos de la escuela y que sacaron\(36\) nombres al azar de esta canasta. De los premiados,\(6\) eran estudiantes de primer año,\(14\) eran estudiantes de segundo año,\(9\) eran juniors, y\(7\) eran seniors. Los resultados no te parecen tan aleatorios. Crees que es un poco sospechoso que los estudiantes de segundo año organizaran la rifa y además ganaran la mayor cantidad de premios. Tu escuela está compuesta por\(30\%\) estudiantes de primer año,\(25\%\) segundo año,\(25\%\) juniors y\(20\%\) seniors.

    1. ¿Cuáles son las frecuencias esperadas de los ganadores de cada clase?
    2. Realizar una prueba de significancia para determinar si los ganadores de los premios se distribuyeron a lo largo de las clases como se esperaría con base en el porcentaje de alumnos en cada grupo. Reporta tu Chi Square y\(p\) valores.
    3. ¿Qué concluyes? (sección pertinente)

    Q6

    Algunos padres de las pequeñas ligas de West Bay piensan que están notando un patrón. Parece haber una relación entre el número de las camisetas de los niños y su posición. Estos padres deciden grabar lo que ven. Los datos hipotéticos aparecen a continuación. Realizar una prueba de Chi Square para determinar si la sospecha de los padres de que existe una relación entre el número de camiseta y la posición es correcta. Denuncia tus valores de Chi Square y p. (sección pertinente)
    Infield
    Outfield
    Jarra
    Total
    0-9
    12
    5
    5
    22
    10-19
    5
    10
    2
    17
    20+
    4
    4
    7
    15
    Total
    21
    19
    14
    54

    Q7

    Verdadero/falso: Una distribución de Chi Cuadrado con\(2\; df\) tiene una media mayor que una distribución de Chi Cuadrado con\(12\; df\). (sección pertinente)

    Q8

    Verdadero/falso: A menudo se utiliza una prueba de Chi Cuadrado para determinar si existe una relación significativa entre dos variables continuas. (sección pertinente)

    Q9

    Verdadero/falso: Imagina que quieres determinar si el spinner que se muestra a continuación está sesgado. La giras\(50\) veces y anotas cuántas veces aterriza la flecha en cada sección. Rechazarás la hipótesis nula en el\(0.05\) nivel y determinarás que este spinner está sesgado si calculas un valor de Chi Cuadrado de\(7.82\) o superior. (sección pertinente)

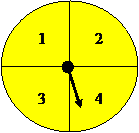
    image001_0002.gif


    Preguntas de casos prácticos

    La siguiente pregunta utiliza datos del estudio de caso SAT y GPA (SG).

    Q10

    Conteste estos ítems para determinar si los puntajes del SAT matemático se distribuyen normalmente. Es posible que desee estandarizar primero los puntajes. (sección pertinente)

    1. Si estos datos se distribuyeran normalmente, cuántas puntuaciones esperarías que hubiera en cada uno de estos paréntesis:
      1. menor que\(1\)\(SD\) por debajo de la media
      2. entre la media y\(1\)\(SD\) por debajo de la media
      3. entre la media y\(1\)\(SD\) por encima de la media
      4. mayor que\(1\)\(SD\) por encima de la media?
    2. ¿Cuántas puntuaciones hay realmente en cada uno de estos paréntesis?
    3. Realizar una prueba de Chi Cuadrado para determinar si los puntajes SAT matemáticos se distribuyen normalmente en función de estas frecuencias esperadas y observadas. (sección pertinente)

    Las siguientes preguntas son del estudio de caso Dieta y Salud (DH).

    Q11

    (DH #3) Realizar una prueba de Pearson Chi Square para determinar si existe alguna relación entre la dieta y el resultado. Reporte la Plaza Chi y\(p\) valores y exponga sus conclusiones. (sección pertinente)

    Las siguientes preguntas son de ARTISTA (reproducidas con permiso).

    artist.gif

    Q12

    Un estudio comparó a miembros de una clínica médica que presentaron denuncias con una muestra aleatoria de miembros que no se quejaron. El estudio dividió a los quejosos en dos subgrupos: los que presentaron denuncias sobre el tratamiento médico y los que presentaron denuncias no médicas. Aquí están los datos sobre el número total en cada grupo y el número que voluntariamente abandonaron la clínica médica. Configure una mesa de dos vías. Analizar estos datos para ver si existe una relación entre queja (no, sí - médica, sí - no médica) y salir de la clínica (sí o no).

    No hay queja Queja Médica Queja No Médica
    Total 743 199 440
    Izquierda 22 26 28

    Q13

    Imagina que crees que existe una relación entre el color de ojos de una persona y donde prefiere sentarse en una gran sala de conferencias. Usted decide recopilar datos de una muestra aleatoria de individuos y realizar una prueba de independencia de chi-cuadrado. ¿Cómo sería tu mesa bidireccional? Use la información para construir dicha tabla y asegúrese de etiquetar los diferentes niveles de cada categoría.

    Q14

    Un geólogo recolecta piezas de piedra caliza del tamaño de una muestra manual de un área en particular. Se realiza una evaluación cualitativa tanto de la textura como del color con los siguientes resultados. ¿Hay evidencia de asociación entre color y textura para estas calizas? Explica tu respuesta.

    Color

    Textura

    Luz

    Mediano

    Oscuro

    Fina

    4

    20

    8

    Mediano

    5

    23

    12

    Grueso

    21

    23

    4

    Q15

    Supongamos que se pide a los estudiantes universitarios que identifiquen sus preferencias en la afiliación política (demócrata, republicana o independiente) y en el helado (chocolate, vainilla o fresa). Supongamos que sus respuestas están representadas en la siguiente tabla bidireccional (con algunos de los totales dejados para que usted calcule).

    Chocolate Vainilla Fresa Total
    Demócrata 26 43 13 82
    Republicano 45 12 8 65
    Independiente 9 13 4
    Total 68 25 173
    1. ¿Qué proporción de los encuestados prefiere el helado de chocolate?
    2. ¿Qué proporción de los encuestados son Independientes?
    3. ¿Qué proporción de Independientes prefiere el helado de chocolate?
    4. ¿Qué proporción de quienes prefieren el helado de chocolate son Independientes?
    5. Analizar los datos para determinar si existe una relación entre preferencia de partido político y preferencia de helado.

    Q16

    La NCAA recopiló datos sobre las tasas de graduación de los atletas en la División I a mediados\(1980s\). Entre\(2,332\) los hombres, no se\(1,343\) había graduado de la universidad, y entre\(959\) las mujeres, no se\(441\) había graduado.

    1. Establecer una mesa bidireccional para examinar la relación entre género y graduación.
    2. Identificar un procedimiento de prueba que sea apropiado para analizar la relación entre género y graduación. Realizar el trámite y exponer su conclusión.

    Seleccionar respuestas

    S3

    1. \(\text{Chi Square} = 16.0\),\(df = 5\)

    S4

    1. Celda para Incontinente/Fumador:\(96.2\)

    S5

    1. \(p = 0.18\)

    S6

    \(\text{Chi Square} = 10.2\)

    S10

      1. Puntajes menores que\(1\)\(SD\) por debajo de la media:\(24\)

    S11

    \(\text{Chi Square} = 16.6\)

    This page titled 17.7: Chi Cuadrado (Ejercicios) is shared under a Public Domain license and was authored, remixed, and/or curated by David Lane via source content that was edited to the style and standards of the LibreTexts platform.