3.3: Eventos Independientes y Mutuamente Exclusivos
- Page ID
- 153208
Independiente y mutuamente excluyente no significan lo mismo.
Eventos Independientes
Dos eventos son independientes si son ciertos los siguientes:
- \(P(\text{A|B}) = P(\text{A})\)
- \(P(\text{B|A}) = P(\text{B})\)
- \(P(\text{A AND B}) = P(\text{A})P(\text{B})\)
Dos eventos\(\text{A}\) y\(\text{B}\) son independientes si el conocimiento de que uno ocurrió no afecta la posibilidad de que ocurra el otro. Por ejemplo, los resultados de dos roles de un dado justo son eventos independientes. El resultado de la primera tirada no cambia la probabilidad del resultado de la segunda tirada. Para mostrar que dos eventos son independientes, debes mostrar solo una de las condiciones anteriores. Si dos eventos NO son independientes, entonces decimos que son dependientes.
Muestreo de una población
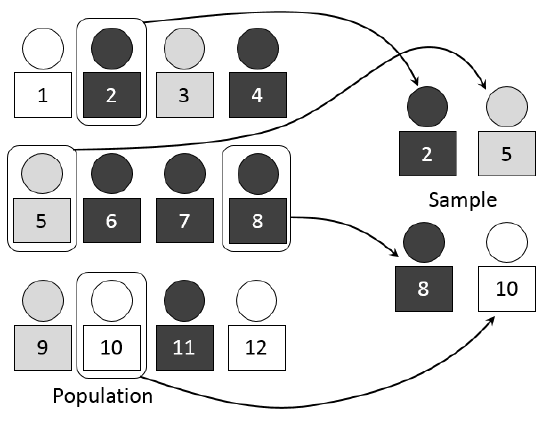
El muestreo se puede realizar con reemplazo o sin reemplazo (Figura\(\PageIndex{1}\)):
- Con reemplazo: Si cada miembro de una población es reemplazado después de ser escogido, entonces ese miembro tiene la posibilidad de ser elegido más de una vez. Cuando el muestreo se realiza con reemplazo, entonces los eventos se consideran independientes, lo que significa que el resultado de la primera selección no cambiará las probabilidades para la segunda selección.
- Sin reemplazo: Cuando el muestreo se realiza sin reemplazo, cada miembro de una población podrá ser elegido solo una vez. En este caso, las probabilidades para el segundo pick se ven afectadas por el resultado de la primera selección. Los eventos se consideran dependientes o no independientes.
Si no se sabe si\(\text{A}\) y\(\text{B}\) son independientes o dependientes, asume que son dependientes hasta que puedas mostrar lo contrario.
Ejemplo\(\PageIndex{1}\): Sampling with and without replacement
Tienes una baraja justa y bien barajada de 52 cartas. Consta de cuatro trajes. Los trajes son palos, diamantes, corazones y espadas. Hay 13 cartas en cada palo que consisten en 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,\(\text{J}\) (jack),\(\text{Q}\) (reina),\(\text{K}\) (rey) de ese palo.
a. Muestreo con reemplazo:
Supongamos que elige tres tarjetas con reemplazo. La primera carta que elijas de las 52 cartas es la\(\text{Q}\) de picas. Vuelves a poner esta carta, reorganizar las cartas y elegir una segunda carta de la baraja de 52 cartas. Es el diez de los clubes. Vuelves a poner esta carta, reorganizar las cartas y elegir una tercera carta de la baraja de 52 cartas. Esta vez, la carta vuelve a ser la\(\text{Q}\) de picas. Tus púas son {\(\text{Q}\)de espadas, diez de palos,\(\text{Q}\) de espadas}. Has escogido el\(\text{Q}\) de picas dos veces. Usted elige cada carta de la baraja de 52 cartas.
b. Muestreo sin reemplazo:
Supongamos que elige tres tarjetas sin reemplazo. La primera carta que escojas de las 52 tarjetas es la\(\text{K}\) de corazones. Pones esta carta a un lado y escoges la segunda carta de las 51 cartas que quedan en la baraja. Son los tres de los diamantes. Pones esta carta a un lado y escoges la tercera carta de las 50 cartas restantes de la baraja. La tercera carta es la\(\text{J}\) de picas. Tus púas son {\(\text{K}\)de corazones, tres de diamantes,\(\text{J}\) de espadas}. Debido a que has elegido las tarjetas sin reemplazo, no puedes recoger la misma tarjeta dos veces.
Ejercicio\(\PageIndex{1}\)
Tienes una baraja justa y bien barajada de 52 cartas. Consta de cuatro trajes. Los trajes son palos, diamantes, corazones y espadas. Hay 13 cartas en cada palo que consisten en 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,\(\text{J}\) (jack),\(\text{Q}\) (reina),\(\text{K}\) (rey) de ese palo. Tres cartas son escogidas al azar.
- Supongamos que sabes que las cartas escogidas son\(\text{Q}\) de espadas,\(\text{K}\) de corazones y\(\text{Q}\) de espadas. ¿Se puede decidir si el muestreo fue con o sin reemplazo?
- Supongamos que sabes que las cartas escogidas son\(\text{Q}\) de espadas,\(\text{K}\) de corazones, y\(\text{J}\) de espadas. ¿Se puede decidir si el muestreo fue con o sin reemplazo?
- Contestar a
-
Con reemplazo
- Respuesta b
-
No
Ejemplo\(\PageIndex{2}\)
Tienes una baraja justa y bien barajada de 52 cartas. Consta de cuatro trajes. Los trajes son palos, diamantes, corazones y espadas. Hay 13 cartas en cada palo que consisten en 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,\(\text{J}\) (jack),\(\text{Q}\) (reina) y\(\text{K}\) (rey) de ese palo. \(\text{S} =\)picas,\(\text{H} =\) Corazones,\(\text{D} =\) Diamantes,\(\text{C} =\) Clubes.
- Supongamos que eliges cuatro cartas, pero no vuelvas a poner ninguna carta en la baraja. Tus tarjetas son\(\text{QS}, 1\text{D}, 1\text{C}, \text{QD}\).
- Supongamos que eliges cuatro cartas y vuelves a poner cada carta antes de elegir la siguiente carta. Tus tarjetas son\(\text{KH}, 7\text{D}, 6\text{D}, \text{KH}\).
¿Cuál de a. o b. tomó una muestra con reemplazo y cuál tomó la muestra sin reemplazo?
- Contestar a
-
Sin reemplazo
- Respuesta b
-
Con reemplazo
Ejercicio\(\PageIndex{2}\)
Tienes una baraja justa y bien barajada de 52 cartas. Consta de cuatro trajes. Los trajes son palos, diamantes, corazones y espadas. Hay 13 cartas en cada palo que consisten en 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,\(\text{J}\) (jack),\(\text{Q}\) (reina) y\(\text{K}\) (rey) de ese palo. \(\text{S} =\)picas,\(\text{H} =\) Corazones,\(\text{D} =\) Diamantes,\(\text{C} =\) Clubes. Supongamos que muestres cuatro tarjetas sin reemplazo. ¿Cuáles de los siguientes resultados son posibles? Responda la misma pregunta para el muestreo con reemplazo.
- \(\text{QS}, 1\text{D}, 1\text{C}, \text{QD}\)
- \(\text{KH}, 7\text{D}, 6\text{D}, \text{KH}\)
- \(\text{QS}, 7\text{D}, 6\text{D}, \text{KS}\)
- Respuesta - sin reemplazo
-
a. Posible; b. Imposible, c. Posible
- Respuesta - con reemplazo
-
a. Posible; c. Posible, c. Posible
Eventos mutuamente excluyentes
\(\text{A}\)y\(\text{B}\) son eventos mutuamente excluyentes si no pueden ocurrir al mismo tiempo. Esto significa que\(\text{A}\) y\(\text{B}\) no comparten ningún resultado y\(P(\text{A AND B}) = 0\).
Por ejemplo, supongamos que el espacio de muestra
\[S = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. \nonumber\]
Vamos\(\text{A} = \{1, 2, 3, 4, 5\}, \text{B} = \{4, 5, 6, 7, 8\}\), y\(\text{C} = \{7, 9\}\). \(\text{A AND B} = \{4, 5\}\).
\[P(\text{A AND B}) = \dfrac{2}{10} \nonumber\]
y no es igual a cero. Por lo tanto,\(\text{A}\) y no\(\text{B}\) son mutuamente excluyentes. \(\text{A}\)y\(\text{C}\) no tienen ningún número en común así\(P(\text{A AND C}) = 0\). Por lo tanto,\(\text{A}\) y\(\text{C}\) son mutuamente excluyentes.
Si no se sabe si\(\text{A}\) y\(\text{B}\) son mutuamente excluyentes, asuma que no lo son hasta que puedas demostrar lo contrario. Los siguientes ejemplos ilustran estas definiciones y términos.
Ejemplo\(\PageIndex{3}\)
Voltear dos monedas justas.
El espacio muestral es\(\{HH, HT, TH, TT\}\) donde\(T =\) las colas y\(H =\) las cabezas. Los resultados son\(HH,HT, TH\), y\(TT\). Los resultados\(HT\) y\(TH\) son diferentes. El\(HT\) significa que la primera moneda mostró cabezas y la segunda moneda mostró colas. El\(TH\) significa que la primera moneda mostró colas y la segunda moneda mostró cabezas.
- Deja que\(\text{A} =\) el evento de conseguir como máximo una cola. (A lo sumo, una cola significa cero o una cola.) Entonces\(\text{A}\) se puede escribir como\(\{HH, HT, TH\}\). El resultado\(HH\) muestra colas cero. \(HT\)y\(TH\) cada uno muestra una cola.
- Deja que\(\text{B} =\) el evento de conseguir todas las colas. \(\text{B}\)se puede escribir como\(\{TT\}\). \(\text{B}\)es el complemento de\(\text{A}\), entonces\(\text{B} = \text{A′}\). También,\(P(\text{A}) + P(\text{B}) = P(\text{A}) + P(\text{A′}) = 1\).
- Las probabilidades para\(\text{A}\) y para\(\text{B}\) son\(P(\text{A}) = \dfrac{3}{4}\) y\(P(\text{B}) = \dfrac{1}{4}\).
- Que\(\text{C} =\) el evento de conseguir todas las cabezas. \(\text{C} = \{HH\}\). Ya que\(\text{B} = \{TT\}\),\(P(\text{B AND C}) = 0\). \(\text{B}\)y Cuidado mutuamente excluyentes. \(\text{B}\)y no\(\text{C}\) tener miembros en común porque no puedes tener todas las colas y todas las cabezas al mismo tiempo.)
- Dejar\(\text{D} =\) evento de conseguir más de una cola. \(\text{D} = \{TT\}\). \(P(\text{D}) = \dfrac{1}{4}\)
- Dejar\(\text{E} =\) evento de conseguir una cabeza en el primer rollo. (Esto implica que puedes obtener una cabeza o una cola en el segundo rollo). \(\text{E} = \{HT, HH\}\). \(P(\text{E}) = \dfrac{2}{4}\)
- Encuentra la probabilidad de obtener al menos una (una o dos) colas en dos volteretas. Dejar\(\text{F} =\) evento de conseguir al menos una cola en dos volteretas. \(\text{F} = \{HT, TH, TT\}\). \(P(\text{F}) = \dfrac{3}{4}\)
Ejercicio\(\PageIndex{3}\)
Roba dos cartas de una baraja estándar de 52 cartas con reemplazo. Encuentra la probabilidad de obtener al menos una tarjeta negra.
- Contestar
-
El espacio de muestra de dibujar dos cartas con reemplazo de una baraja estándar de 52 cartas con respecto al color es\(\{BB, BR, RB, RR\}\).
Evento\(A =\) Obtener al menos una tarjeta negra\(= \{BB, BR, RB\}\)
\(P(\text{A}) = \dfrac{3}{4} = 0.75\)
Ejemplo\(\PageIndex{4}\)
Voltear dos monedas justas. Encuentra las probabilidades de los eventos.
- Deje que\(\text{F} =\) el evento de obtener como máximo una cola (cero o una cola).
- Que\(\text{G} =\) el suceso de conseguir dos caras que son iguales.
- Dejar que\(\text{H} =\) el evento de conseguir una cabeza en el primer volteo seguido de una cabeza o cola en el segundo volteo.
- ¿Son\(\text{F}\) y\(\text{G}\) mutuamente excluyentes?
- Deja que\(\text{J} =\) el evento de conseguir todas las colas. ¿Son\(\text{J}\) y\(\text{H}\) mutuamente excluyentes?
Solución
Mira el espacio de muestra en Ejemplo\(\PageIndex{3}\).
- Cero (0) o una (1) colas ocurren cuando aparecen los resultados\(HH, TH, HT\). \(P(\text{F}) = \dfrac{3}{4}\)
- Dos caras son iguales si\(HH\) o\(TT\) aparecen. \(P(\text{G}) = \dfrac{2}{4}\)
- Una cabeza en el primer volteo seguida de una cabeza o cola en el segundo volteo ocurre cuando\(HH\) o\(HT\) aparece. \(P(\text{H}) = \dfrac{2}{4}\)
- \(\text{F}\)y\(\text{G}\) compartir\(HH\) así no\(P(\text{F AND G})\) es igual a cero (0). \(\text{F}\)y no\(\text{G}\) son mutuamente excluyentes.
- Obtener todas las colas ocurre cuando las colas aparecen en ambas monedas (\(TT\)). \(\text{H}\)los resultados son\(HH\) y\(HT\).
\(\text{J}\)y no\(\text{H}\) tienen nada en común así\(P(\text{J AND H}) = 0\). \(\text{J}\)y\(\text{H}\) son mutuamente excluyentes.
Ejercicio\(\PageIndex{4}\)
Una caja tiene dos bolas, una blanca y otra roja. Seleccionamos una bola, la colocamos de nuevo en la caja y seleccionamos una segunda bola (muestreo con reemplazo). Encuentra la probabilidad de los siguientes eventos:
- Que\(\text{F} =\) el evento de conseguir el balón blanco en dos ocasiones.
- Deja que\(\text{G} =\) el evento de conseguir dos bolas de diferentes colores.
- Deje que\(\text{H} =\) el evento de ponerse blanco en la primera selección.
- ¿Son\(\text{F}\) y\(\text{G}\) mutuamente excluyentes?
- ¿Son\(\text{G}\) y\(\text{H}\) mutuamente excluyentes?
Contestar
- \(P(\text{F}) = \dfrac{1}{4}\)
- \(P(\text{G}) = \dfrac{1}{2}\)
- \(P(\text{H}) = \dfrac{1}{2}\)
- Sí
- No
Ejemplo\(\PageIndex{5}\)
Enrolle un troquel justo de seis lados. El espacio muestral es {1, 2, 3, 4, 5, 6}. Dejar que el evento\(\text{A} =\) una cara sea impar. Entonces\(\text{A} = \{1, 3, 5\}\). Deja que el evento\(\text{B} =\) una cara sea parejo. Entonces\(\text{B} = \{2, 4, 6\}\).
- Encuentra el complemento de\(\text{A}\),\(\text{A′}\). El complemento de\(\text{A}\),\(\text{A′}\), es\(\text{B}\) porque\(\text{A}\) y\(\text{B}\) juntos conforman el espacio muestral. \(P(\text{A}) + P(\text{B}) = P(\text{A}) + P(\text{A′}) = 1\). También,\(P(\text{A}) = \dfrac{3}{6}\) y\(P(\text{B}) = \dfrac{3}{6}\).
- Deje que las caras\(\text{C} =\) impares del evento sean mayores que dos. Entonces\(\text{C} = \{3, 5\}\). Deje que el evento\(\text{D} =\) todo incluso se enfrenta a menos de cinco. Entonces\(\text{D} = \{2, 4\}\). \(P(\text{C AND D}) = 0\)porque no se puede tener una cara impar y par al mismo tiempo. Por lo tanto,\(\text{C}\) y\(\text{D}\) son eventos mutuamente excluyentes.
- Deje que el evento\(\text{E} =\) todas las caras sean menos de cinco. \(\text{E} = \{1, 2, 3, 4\}\).
¿Son\(\text{C}\) y eventos\(\text{E}\) mutuamente excluyentes? (Conteste sí o no.) ¿Por qué o por qué no?
Contestar
No. \(\text{C} = \{3, 5\}\)y\(\text{E} = \{1, 2, 3, 4\}\). \(P(\text{C AND E}) = \dfrac{1}{6}\). Para ser mutuamente excluyentes,\(P(\text{C AND E})\) debe ser cero.
- Encuentra\(P(\text{C|A})\). Esta es una probabilidad condicional. Recordemos que el evento\(\text{C}\) es {3, 5} y el evento\(\text{A}\) es {1, 3, 5}. Para encontrar\(P(\text{C|A})\), encontrar la probabilidad de\(\text{C}\) utilizar el espacio muestral\(\text{A}\). Se ha reducido el espacio muestral del espacio muestral original {1, 2, 3, 4, 5, 6} a {1, 3, 5}. Entonces,\(P(\text{C|A}) = \dfrac{2}{3}\).
Ejercicio\(\PageIndex{5}\)
Deje que el evento\(\text{A} =\) aprenda español. Let event\(\text{B}\) = aprender alemán. Después\(\text{A AND B}\) = aprender español y alemán. Supongamos\(P(\text{A}) = 0.4\) y\(P(\text{B}) = 0.2\). \(P(\text{A AND B}) = 0.08\). ¿Los eventos\(\text{A}\) son\(\text{B}\) independientes? Pista: Debes mostrar UNO de los siguientes:
- \(P(\text{A|B}) = P(\text{A})\)
- \(P(\text{B|A})\)
- \(P(\text{A AND B}) = P(\text{A})P(\text{B})\)
Contestar
\[P(\text{A|B}) = \dfrac{\text{P(A AND B)}}{P(\text{B})} = \dfrac{0.08}{0.2} = 0.4 = P(\text{A})\]
Los eventos son independientes porque\(P(\text{A|B}) = P(\text{A})\).
Ejemplo\(\PageIndex{6}\)
Deje que el evento\(\text{G} =\) tome una clase de matemáticas. Deje que el evento\(\text{H} =\) tome una clase de ciencias. Después,\(\text{G AND H} =\) tomando una clase de matemáticas y una clase de ciencias. Supongamos\(P(\text{G}) = 0.6\)\(P(\text{H}) = 0.5\),, y\(P(\text{G AND H}) = 0.3\). ¿Son\(\text{G}\) e\(\text{H}\) independientes?
Si\(\text{G}\) y\(\text{H}\) son independientes, entonces debes mostrar UNO de los siguientes:
- \(P(\text{G|H}) = P(\text{G})\)
- \(P(\text{H|G}) = P(\text{H})\)
- \(P(\text{G AND H}) = P(\text{G})P(\text{H})\)
La elección que hagas depende de la información que tengas. Puedes elegir cualquiera de los métodos aquí porque tienes la información necesaria.
- a. demuéstralo\(P(\text{G|H}) = P(\text{G})\).
- b. Espectáculo\(P(\text{G AND H}) = P(\text{G})P(\text{H})\).
Solución
- \(P(\text{G|H}) = \dfrac{P(\text{G AND H})}{P(\text{H})} = \dfrac{0.3}{0.5} = 0.6 = P(\text{G})\)
- \(P(\text{G})P(\text{H}) = (0.6)(0.5) = 0.3 = P(\text{G AND H})\)
Desde\(\text{G}\) y\(\text{H}\) son independientes, saber que una persona está tomando una clase de ciencias no cambia la posibilidad de que esté tomando una clase de matemáticas. Si los dos eventos no hubieran sido independientes (es decir, son dependientes) entonces saber que una persona está tomando una clase de ciencias cambiaría la posibilidad de que esté tomando matemáticas. Para la práctica, demuéstralo\(P(\text{H|G}) = P(\text{H})\) para mostrar eso\(\text{G}\) y\(\text{H}\) son eventos independientes.
Ejercicio\(\PageIndex{6}\)
En una bolsa, hay seis canicas rojas y cuatro canicas verdes. Las canicas rojas están marcadas con los números 1, 2, 3, 4, 5 y 6. Las canicas verdes están marcadas con los números 1, 2, 3 y 4.
- \(\text{R} =\)una canica roja
- \(\text{G} =\)un mármol verde
- \(\text{O} =\)una canica impar
- El espacio muestral es\(\text{S} = \{R1, R2, R3, R4, R5, R6, G1, G2, G3, G4\}\).
\(\text{S}\)tiene diez resultados. ¿Qué es\(P(\text{G AND O})\)?
Contestar
Evento\(\text{G}\) y\(\text{O} = \{G1, G3\}\)
\(P(\text{G and O}) = \dfrac{2}{10} = 0.2\)
Ejemplo\(\PageIndex{7}\)
Deje que el evento\(\text{C} =\) tome una clase de inglés. Deje que el evento\(\text{D} =\) tome una clase de discurso.
Supongamos\(P(\text{C}) = 0.75\)\(P(\text{D}) = 0.3\),,\(P(\text{C|D}) = 0.75\) y\(P(\text{C AND D}) = 0.225\).
Justifica numéricamente tus respuestas a las siguientes preguntas.
- ¿Son\(\text{C}\) e\(\text{D}\) independientes?
- ¿Son\(\text{C}\) y\(\text{D}\) mutuamente excluyentes?
- ¿Qué es\(P(\text{D|C})\)?
Solución
- Sí, porque\(P(\text{C|D}) = P(\text{C})\).
- No, porque no\(P(\text{C AND D})\) es igual a cero.
- \(P(\text{D|C}) = \dfrac{P(\text{C AND D})}{P(\text{C})} = \dfrac{0.225}{0.75} = 0.3\)
Ejercicio\(\PageIndex{7}\)
Un estudiante va a la biblioteca. Deje eventos\(\text{B} =\) en los que el estudiante saque un libro y\(\text{D} =\) el estudiante saque un DVD. Supongamos que\(P(\text{B}) = 0.40\),\(P(\text{D}) = 0.30\) y\(P(\text{B AND D}) = 0.20\).
- Encuentra\(P(\text{B|D})\).
- Encuentra\(P(\text{D|B})\).
- ¿Son\(\text{B}\) e\(\text{D}\) independientes?
- ¿Son\(\text{B}\) y\(\text{D}\) mutuamente excluyentes?
Contestar
- \(P(\text{B|D}) = 0.6667\)
- \(P(\text{D|B}) = 0.5\)
- No
- No
Ejemplo\(\PageIndex{8}\)
En una caja hay tres tarjetas rojas y cinco tarjetas azules. Las tarjetas rojas están marcadas con los números 1, 2 y 3, y las tarjetas azules están marcadas con los números 1, 2, 3, 4 y 5. Las cartas están bien barajadas. Alcanzas dentro de la caja (no puedes ver dentro de ella) y rotas una carta.
Let
- \(\text{R =}\)se saca la tarjeta roja,
- \(\text{B} =\)tarjeta azul se dibuja,
- \(\text{E} =\)Se roba una tarjeta par.
El espacio muestral\(S = R1, R2, R3, B1, B2, B3, B4, B5\).
\(S\)tiene ocho resultados.
- \(P(\text{R}) = \dfrac{3}{8}\). \(P(\text{B}) = \dfrac{5}{8}\). \(P(\text{R AND B}) = 0\). (No se puede sacar una carta que sea tanto roja como azul).
- \(P(\text{E}) = \dfrac{3}{8}\). (Hay tres tarjetas pares,\(R2, B2\), y\(B4\).)
- \(P(\text{E|B}) = \dfrac{2}{5}\). (Hay cinco tarjetas azules:\(B1, B2, B3, B4\), y\(B5\). Fuera de las tarjetas azules, hay dos tarjetas pares;\(B2\) y\(B4\).)
- \(P(\text{B|E}) = \dfrac{2}{3}\). (Hay tres tarjetas pares:\(R2, B2\), y\(B4\). Fuera de las tarjetas pares, a son azules;\(B2\) y\(B4\).)
- Los eventos\(\text{R}\) y\(\text{B}\) son mutuamente excluyentes porque\(P(\text{R AND B}) = 0\).
- Dejar\(\text{G} =\) tarjeta con un número mayor a 3. \(\text{G} = \{B4, B5\}\). \(P(\text{G}) = \dfrac{2}{8}\). Dejar tarjeta\(\text{H} =\) azul numerada entre uno y cuatro, inclusive. \(\text{H} = \{B1, B2, B3, B4\}\). \(P(\text{G|H}) = \frac{1}{4}\). (La única tarjeta en la\(\text{H}\) que tiene un número mayor que tres es B4.) Ya que\(\dfrac{2}{8} = \dfrac{1}{4}\),\(P(\text{G}) = P(\text{G|H})\), lo que significa que\(\text{G}\) y\(\text{H}\) son independientes.
Ejercicio\(\PageIndex{8}\)
En una arena de basquetbol,
- El 70% de la afición está apoyando al equipo local.
- El 25% de los abanicos visten de azul.
- El 20% de los aficionados se visten de azul y están apoyando al equipo visitante.
- De los aficionados que enraizan por el equipo visitante, 67% se visten de azul.
Que\(\text{A}\) sea el evento de que un fanático esté enraizando para el equipo visitante.
Que\(\text{B}\) sea el evento de que un fan esté vestido de azul.
¿Son independientes los eventos de enraizar al equipo visitante y vestir azul? ¿Son mutuamente excluyentes?
Contestar
- \(P(\text{B|A}) = 0.67\)
- \(P(\text{B}) = 0.25\)
Entonces\(P(\text{B})\) no iguala lo\(P(\text{B|A})\) que significa que no\(\text{B} and \text{A}\) son independientes (vestir de azul y enraizamiento para el equipo visitante no son independientes). Tampoco son mutuamente excluyentes, porque\(P(\text{B AND A}) = 0.20\), no\(0\).
Ejemplo\(\PageIndex{9}\)
En una clase universitaria particular, el 60% de los estudiantes son mujeres. El cincuenta por ciento de todos los estudiantes de la clase tienen el pelo largo. Cuarenta y cinco por ciento de los estudiantes son mujeres y tienen el pelo largo. De las alumnas, 75% tienen el pelo largo. Que\(\text{F}\) sea el evento de que una estudiante sea femenina. Que\(\text{L}\) sea el evento de que un estudiante tenga el pelo largo. Un estudiante es escogido al azar. ¿Los eventos de ser mujer y tener el pelo largo son independientes?
- En este ejemplo se dan las siguientes probabilidades:
- \(P(\text{F}) = 0.60\);\(P(\text{L}) = 0.50\)
- \(P(\text{F AND L}) = 0.45\)
- \(P(\text{L|F}) = 0.75\)
La elección que hagas depende de la información que tengas. Podrías usar la primera o última condición de la lista para este ejemplo. \(P(\text{F|L})\)Aún no lo sabes, así que no puedes usar la segunda condición.
Solución 1
Comprobar si\(P(\text{F AND L}) = P(\text{F})P(\text{L})\). Se nos da eso\(P(\text{F AND L}) = 0.45\), pero\(P(\text{F})P(\text{L}) = (0.60)(0.50) = 0.30\). Los eventos de ser mujer y tener el pelo largo no son independientes porque\(P(\text{F AND L})\) no es igual\(P(\text{F})P(\text{L})\).
Solución 2
Comprobar si\(P(\text{L|F})\) es igual\(P(\text{L})\). Se nos da eso\(P(\text{L|F}) = 0.75\), pero\(P(\text{L}) = 0.50\); no son iguales. Los eventos de ser mujer y tener el pelo largo no son independientes.
Interpretación de los resultados
Los eventos de ser mujer y tener el pelo largo no son independientes; saber que un estudiante es femenino cambia la probabilidad de que un estudiante tenga el pelo largo.
Ejercicio\(\PageIndex{9}\)
Mark está decidiendo qué ruta tomar para trabajar. Sus elecciones son\(\text{I} = \text{the Interstate}\) y\(\text{F} = \text{Fifth Street}\)
- \(P(\text{I}) = 0.44\)y\(P(\text{F}) = 0.55\)
- \(P(\text{I AND F}) = 0\)porque Mark tomará solo una ruta para trabajar.
¿Cuál es la probabilidad de\(P(\text{I OR F})\)?
Contestar
Porque\(P(\text{I AND F}) = 0\),
\(P(\text{I OR F}) = P(\text{I}) + P(\text{F}) - P(\text{I AND F}) = 0.44 + 0.56 - 0 = 1\)
Ejemplo\(\PageIndex{10}\)
- Lanzar una moneda justa (la moneda tiene dos caras,\(\text{H}\) y\(\text{T}\)). Los resultados son ________. Contar los resultados. Hay ____ resultados.
- Lanzar un dado justo de seis lados (el dado tiene 1, 2, 3, 4, 5 o 6 puntos en un lado). Los resultados son ________________. Contar los resultados. Hay ___ resultados.
- Multiplique los dos números de resultados. La respuesta es _______.
- Si volteas una moneda justa y la sigues con el lanzamiento de un dado justo de seis lados, la respuesta en tres es el número de resultados (tamaño del espacio muestral). ¿Cuáles son los resultados? (Pista: Dos de los resultados son\(H1\) y\(T6\).)
- \(\text{A} =\)Cabezas de evento (\(\text{H}\)) en la moneda seguidas de un número par (2, 4, 6) en el dado.
\(\text{A}\)= {_________________}. Encuentra\(P(\text{A})\). - El evento se\(\text{B} =\) encabeza en la moneda seguido de un tres en el dado. \(\text{B} =\){________}. Encuentra\(P(\text{B})\).
- ¿Son\(\text{A}\) y\(\text{B}\) mutuamente excluyentes? (Pista: ¿Qué es\(P(\text{A AND B})\)? Si\(P(\text{A AND B}) = 0\), entonces\(\text{A}\) y\(\text{B}\) son mutuamente excluyentes.)
- ¿Son\(\text{A}\) e\(\text{B}\) independientes? (Pista: ¿Es\(P(\text{A AND B}) = P(\text{A})P(\text{B})\)? Si\(P(\text{A AND B})\ = P(\text{A})P(\text{B})\), entonces\(\text{A}\) y\(\text{B}\) son independientes. Si no, entonces son dependientes).
Solución
- \(\text{H}\)y\(\text{T}\); 2
- 1, 2, 3, 4, 5, 6; 6
- 2 (6) = 12
- \(T1, T2, T3, T4, T5, T6, H1, H2, H3, H4, H5, H6\)
- \(\text{A} = \{H2, H4, H6\}\);\(P(\text{A}) = \dfrac{3}{12}\)
- \(\text{B} = \{H3\}\);\(P(\text{B}) = \dfrac{1}{12}\)
- Sí, porque\(P(\text{A AND B}) = 0\)
- \(P(\text{A AND B}) = 0\). \(P(\text{A})P(\text{B}) = \left(\dfrac{3}{12}\right)\left(\dfrac{1}{12}\right)\). \(P(\text{A AND B})\)no es igual\(P(\text{A})P(\text{B})\), entonces\(\text{A}\) y\(\text{B}\) son dependientes.
Ejercicio\(\PageIndex{10}\)
Una caja tiene dos bolas, una blanca y otra roja. Seleccionamos una bola, la colocamos de nuevo en la caja y seleccionamos una segunda bola (muestreo con reemplazo). \(\text{T}\)Sea el evento de conseguir el balón blanco dos veces,\(\text{F}\) el evento de recoger primero el balón blanco,\(\text{S}\) el evento de recoger el balón blanco en el segundo sorteo.
- Cómputos\(P(\text{T})\).
- Cómputos\(P(\text{T|F})\).
- ¿Son\(\text{T}\) e\(\text{F}\) independientes?.
- ¿Son\(\text{F}\) y\(\text{S}\) mutuamente excluyentes?
- ¿Son\(\text{F}\) e\(\text{S}\) independientes?
Contestar
- \(P(\text{T}) = \dfrac{1}{4}\)
- \(P(\text{T|F}) = \dfrac{1}{2}\)
- No
- No
- Sí
Referencias
- López, Shane, Preety Sidhu. “Los maestros estadounidenses aman sus vidas, pero luchan en el lugar de trabajo”. Bienestar Gallup, 2013. http://www.gallup.com/poll/161516/te...workplace.aspx (consultado el 2 de mayo de 2013).
- Datos de Gallup. Disponible en línea en www.gallup.com/ (consultado el 2 de mayo de 2013).
Revisar
Dos eventos\(\text{A}\) y\(\text{B}\) son independientes si el conocimiento de que uno ocurrió no afecta la posibilidad de que ocurra el otro. Si dos eventos no son independientes, entonces decimos que son dependientes.
En el muestreo con reemplazo, cada miembro de una población es reemplazado después de ser escogido, por lo que ese miembro tiene la posibilidad de ser elegido más de una vez, y los eventos se consideran independientes. En el muestreo sin reemplazo, cada miembro de una población podrá ser elegido solo una vez, y los eventos se consideran no independientes. Cuando los eventos no comparten resultados, se excluyen mutuamente entre sí.
Revisión de Fórmula
- Si\(\text{A}\) y\(\text{B}\) son independientes,\(P(\text{A AND B}) = P(\text{A})P(\text{B}), P(\text{A|B}) = P(\text{A})\) y\(P(\text{B|A}) = P(\text{B})\).
- Si\(\text{A}\) y\(\text{B}\) son mutuamente excluyentes,\(P(\text{A OR B}) = P(\text{A}) + P(\text{B}) and P(\text{A AND B}) = 0\).
Ejercicio\(\PageIndex{11}\)
\(\text{E}\)y\(\text{F}\) son eventos mutuamente excluyentes. \(P(\text{E}) = 0.4\);\(P(\text{F}) = 0.5\). Encuentra\(P(\text{E∣F})\).
Ejercicio\(\PageIndex{12}\)
\(\text{J}\)y\(\text{K}\) son eventos independientes. \(P(\text{J|K}) = 0.3\). Encuentra\(P(\text{J})\).
Contestar
\(P(\text{J}) = 0.3\)
Ejercicio\(\PageIndex{13}\)
\(\text{U}\)y\(\text{V}\) son eventos mutuamente excluyentes. \(P(\text{U}) = 0.26\);\(P(\text{V}) = 0.37\). Encuentra:
- \(P(\text{U AND V}) =\)
- \(P(\text{U|V}) =\)
- \(P(\text{U OR V}) =\)
Ejercicio\(\PageIndex{14}\)
\(\text{Q}\)y\(\text{R}\) son eventos independientes. \(P(\text{Q}) = 0.4\)y\(P(\text{Q AND R}) = 0.1\). Encuentra\(P(\text{R})\).
Contestar
\(P(\text{Q AND R}) = P(\text{Q})P(\text{R})\)
\(0.1 = (0.4)P(\text{R})\)
\(P(\text{R}) = 0.25\)
Reuniéndolo
Ejercicio\(\PageIndex{16}\)
Un año anterior, los pesos de los integrantes de los 49ers de San Francisco y los Dallas Cowboys se publicaron en el San Jose Mercury News. Los datos fácticos se compilan en Tabla.
| Camisa# | ≤ 210 | 211—250 | 251—290 | 290≤ |
|---|---|---|---|---|
| 1—33 | 21 | 5 | 0 | 0 |
| 34—66 | 6 | 18 | 7 | 4 |
| 66—99 | 6 | 12 | 22 | 5 |
Para lo siguiente, supongamos que seleccionas al azar a un jugador entre los 49ers o Cowboys.
Si tener un número de playera del uno al 33 y que pesara como máximo 210 libras eran eventos independientes, entonces, ¿de qué debería ser cierto\(P(\text{Shirt} \#1–33|\leq 210 \text{ pounds})\)?
Ejercicio\(\PageIndex{17}\)
La probabilidad de que un varón desarrolle alguna forma de cáncer en su vida es de 0.4567. La probabilidad de que un varón tenga al menos un resultado de prueba falso positivo (es decir, la prueba regresa por cáncer cuando el hombre no lo tiene) es de 0.51. Algunas de las siguientes preguntas no tienen suficiente información para que las respondas. Escribe “no suficiente información” para esas respuestas. Que\(\text{C} =\) un hombre desarrolle cáncer en su vida y el\(\text{P} =\) hombre tenga al menos un falso positivo.
- \(P(\text{C}) =\)______
- \(P(\text{P|C}) =\)______
- \(P(\text{P|C'}) =\)______
- Si una prueba sale positiva, basada en valores numéricos, ¿se puede suponer que el hombre tiene cáncer? Justificar numéricamente y explicar por qué o por qué no.
Contestar
- \(P(\text{C}) = 0.4567\)
- no hay suficiente información
- no hay suficiente información
- No, porque más de la mitad (0.51) de los hombres tienen al menos un texto falso positivo
Ejercicio\(\PageIndex{18}\)
Dados los eventos\(\text{G}\) y\(\text{H}: P(\text{G}) = 0.43\)\(P(\text{H}) = 0.26\);\(P(\text{H AND G}) = 0.14\)
- Encuentra\(P(\text{H OR G})\).
- Encuentra la probabilidad del complemento del evento (\(\text{H AND G}\)).
- Encuentra la probabilidad del complemento del evento (\(\text{H OR G}\)).
Ejercicio\(\PageIndex{19}\)
Dados los eventos\(\text{J}\) y\(\text{K}: P(\text{J}) = 0.18\)\(P(\text{K}) = 0.37\);\(P(\text{J OR K}) = 0.45\)
- Encuentra\(P(\text{J AND K})\).
- Encuentra la probabilidad del complemento del evento (\(\text{J AND K}\)).
- Encuentra la probabilidad del complemento del evento (\(\text{J AND K}\)).
Contestar
- \(P(\text{J OR K}) = P(\text{J}) + P(\text{K}) − P(\text{J AND K}); 0.45 = 0.18 + 0.37 - P(\text{J AND K})\); resolver para encontrar\(P(\text{J AND K}) = 0.10\)
- \(P(\text{NOT (J AND K)}) = 1 - P(\text{J AND K}) = 1 - 0.10 = 0.90\)
- \(P(\text{NOT (J OR K)}) = 1 - P(\text{J OR K}) = 1 - 0.45 = 0.55\)
Glosario
- Eventos Dependientes
- Si dos eventos NO son independientes, entonces decimos que son dependientes.
- Muestreo con Repuesto
- Si cada miembro de una población es reemplazado después de ser escogido, entonces ese miembro tiene la posibilidad de ser elegido más de una vez.
- Muestreo sin Repuesto
- Cuando el muestreo se realiza sin reemplazo, cada miembro de una población podrá ser elegido sólo una vez.
- La probabilidad condicional de un evento dado otro evento
- P (A | B) es la probabilidad de que ocurra el evento A dado que el evento B ya ocurrió.
- El quiróder de dos eventos
- Un resultado es en el evento A O B si el resultado está en A, está en B, o está tanto en A como en B.


