4.5: Distribución geométrica
- Page ID
- 153174
Hay tres características principales de un experimento geométrico.
- Hay uno o más juicios de Bernoulli con todos los fracasos excepto el último, lo cual es un éxito. En otras palabras, sigues repitiendo lo que estás haciendo hasta el primer éxito. Entonces te detienes. Por ejemplo, lanzas un dardo a una diana hasta que golpeas la diana. La primera vez que golpeas la diana es un “éxito” así que dejas de lanzar el dardo. Podría tomar seis intentos hasta que golpees la diana. Se puede pensar en los juicios como fracaso, fracaso, fracaso, fracaso, éxito, STOP.
- En teoría, el número de juicios podría continuar para siempre. Debe haber al menos un juicio.
- La probabilidad,\(p\), de un éxito y la probabilidad,\(q\), de un fracaso es la misma para cada ensayo. \(p + q = 1\)y\(q = 1 − p\). Por ejemplo, la probabilidad de rodar un tres cuando lanzas un dado justo es\(\dfrac{1}{6}\). Esto es cierto sin importar cuántas veces rodes el dado. Supongamos que quieres saber la probabilidad de conseguir los tres primeros en el quinto rollo. En rollos uno a cuatro, no se obtiene una cara con un tres. La probabilidad para cada uno de los rollos es\(q = \dfrac{5}{6}\), la probabilidad de un fallo. La probabilidad de conseguir un tres en el quinto rollo es\(\left(\dfrac{5}{6}\right)\left(\dfrac{5}{6}\right)\left(\dfrac{5}{6}\right)\left(\dfrac{5}{6}\right)\left(\dfrac{1}{6}\right) = 0.0804\).
\(X =\)el número de juicios independientes hasta el primer éxito.
Juegas un juego de azar que puedes ganar o perder (no hay otras posibilidades) hasta que pierdes. Tu probabilidad de perder es\(p = 0.57\). ¿Cuál es la probabilidad de que tarden cinco juegos hasta que pierdes? Deja que\(X =\) el número de juegos que juegues hasta que pierdas (incluye el juego perdedor). Después\(X\) toma los valores 1, 2, 3,... (podría continuar indefinidamente). La pregunta de probabilidad es\(P(x = 5)\).
Ejemplo\(\PageIndex{1}\)
Juegas un juego de azar que puedes ganar o perder (no hay otras posibilidades) hasta que pierdes. Tu probabilidad de perder es\(p = 0.57\). ¿Cuál es la probabilidad de que tarden cinco juegos hasta que pierdes? Deja que\(X =\) el número de juegos que juegues hasta que pierdas (incluye el juego perdedor). Después\(X\) toma los valores 1, 2, 3,... (podría continuar indefinidamente). La pregunta de probabilidad es\(P(x = 5)\).
Ejercicio\(\PageIndex{1}\)
Lanza dardos a una tabla hasta que golpeas el área central. Tu probabilidad de golpear el área central es\(p = 0.17\). Quieres encontrar la probabilidad de que tarden ocho lanzamientos hasta que golpees al centro. ¿Qué\(X\) valores adquiere?
Responder
\(1, 2, 3, 4, \dotsc, n\). Puede continuar indefinidamente.
Ejemplo\(\PageIndex{2}\)
Una ingeniera de seguridad siente que el 35% de todos los accidentes industriales en su planta son causados por el hecho de que los empleados no sigan las instrucciones. Ella decide mirar los reportes de accidentes (seleccionados al azar y reemplazados en la pila después de leer) hasta encontrar uno que muestre un accidente causado por el hecho de que los empleados no sigan las instrucciones. En promedio, ¿cuántos informes esperaría mirar la ingeniera de seguridad hasta que encuentre un reporte que muestre un accidente causado por la falta de seguimiento de las instrucciones de los empleados? ¿Cuál es la probabilidad de que la ingeniera de seguridad tenga que examinar al menos tres reportes hasta que encuentre un reporte que muestre un accidente causado por el incumplimiento de las instrucciones del empleado?
Let\(X\) = el número de accidentes que el ingeniero de seguridad debe examinar hasta que encuentre un reporte que muestre un accidente causado por la falta de seguimiento de las instrucciones del empleado. \(X\)toma los valores 1, 2, 3,... La primera pregunta te pide encontrar el valor esperado o la media. La segunda pregunta te pide que encuentres\(P(x \geq 3)\). (“Al menos” se traduce como un símbolo “mayor que o igual a”).
Ejercicio\(\PageIndex{2}\)
Un instructor siente que el 15% de los estudiantes obtienen por debajo de una C en su examen final. Ella decide mirar los exámenes finales (seleccionados aleatoriamente y reemplazados en la pila después de leer) hasta encontrar uno que muestre una calificación por debajo de una C. Queremos saber la probabilidad de que la instructora tenga que examinar al menos diez exámenes hasta que encuentre uno con una calificación por debajo de una C. ¿Cuál es la pregunta de probabilidad expresado matemáticamente?
Responder
\(P(x \leq 10)\)
Ejemplo\(\PageIndex{3}\)
Supongamos que estás buscando un estudiante en tu universidad que viva a menos de cinco millas de ti. Sabes que el 55% de los 25 mil estudiantes viven a menos de cinco millas de ti. Te comunicas aleatoriamente con estudiantes de la universidad hasta que uno dice que vive a menos de cinco millas de ti. ¿Cuál es la probabilidad de que necesites contactar a cuatro personas?
Este es un problema geométrico porque es posible que tengas una serie de fallas antes de tener el único éxito que deseas. Además, la probabilidad de éxito se mantiene igual cada vez que le preguntas a un estudiante si vive a menos de cinco millas de ti. No hay un número definido de pruebas (número de veces que le preguntas a un estudiante).
- Deja que\(X =\) el número de ____________ debes preguntar ____________ uno dice que sí.
- ¿Qué\(X\) valores adquiere?
- ¿Qué son\(p\) y\(q\)?
- La pregunta de probabilidad es\(P(\) _______\()\).
Solución
- Deja\(X =\) el número de alumnos que debes preguntar hasta que uno diga que sí.
- 1, 2, 3,..., (número total de alumnos)
- \(p = 0.55; q = 0.45\)
- \(P(x = 4)\)
Ejercicio\(\PageIndex{3}\)
Necesitas encontrar una tienda que lleve una tinta especial para impresora. Ya sabes que de las tiendas que llevan tinta de impresora, 10% de ellas llevan la tinta especial. Llamas aleatoriamente a cada tienda hasta que una tenga la tinta que necesitas. ¿Qué son\(p\) y\(q\)?
Responder
\(p = 0.1\)
\(q = 0.9\)
Notación para el Geométrico:\(G =\) Geometric Probability Distribution Function
\(X \sim G(p)\)
Lee esto como "\(X\)es una variable aleatoria con una distribución geométrica”. El parámetro es\(p\);\(p =\) la probabilidad de éxito para cada ensayo.
Ejemplo\(\PageIndex{4}\)
Supongamos que la probabilidad de un componente informático defectuoso es 0.02. Los componentes se seleccionan aleatoriamente. Encuentra la probabilidad de que el primer defecto sea causado por el séptimo componente probado. ¿Cuántos componentes espera probar hasta que uno se encuentre defectuoso?
Let\(X\) = el número de componentes de computadora probados hasta que se encuentre el primer defecto.
\(X\)toma los valores 1, 2, 3,... donde\(p = 0.02\). \(X \sim G(0.02)\)
Encontrar\(P(x = 7)\). \(P(x = 7) = 0.0177\).
Para encontrar la probabilidad de que\(x = 7\),
- Entrar 2 nd, DISTR.C/
- Desplázate hacia abajo y selecciona geometpdf (
- Presione ENTER
- Escriba 0.02, 7); presione ENTRAR para ver el resultado:\(P(x = 7) = 0.0177\)
Para encontrar la probabilidad de que\(x \leq 7\), siga las mismas instrucciones EXCEPTO seleccionar E: geometcdf como la función de distribución.
La probabilidad de que el séptimo componente sea el primer defecto es 0.0177.
La gráfica de\(X \sim G(0.02)\) es:
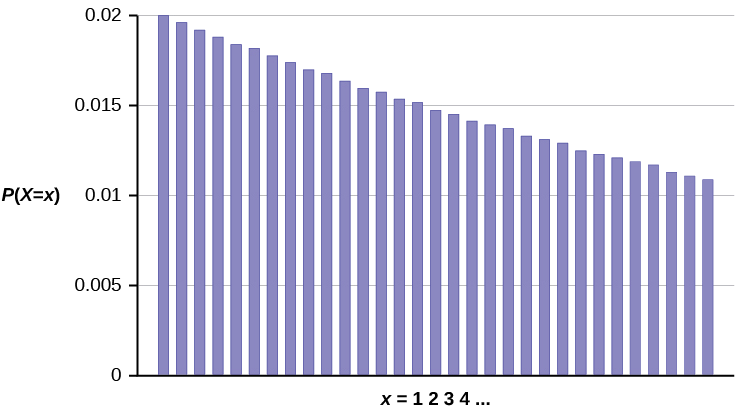
El eje y contiene la probabilidad de\(x\), donde\(X =\) el número de componentes informáticos probados.
El número de componentes que esperarías probar hasta encontrar el primero defectuoso es la media,\(\mu = 50\).
La fórmula para la media es
\[\mu = \dfrac{1}{\text{p}} = \dfrac{1}{0.02} = 50\]
La fórmula para la varianza es
\[\sigma^{2} = \left(\dfrac{1}{p}\right)\left(\dfrac{1}{p} - 1 \right) = \left(\dfrac{1}{0.02}\right)\left(\dfrac{1}{0.02} - 1 \right) = 2,450\]
La desviación estándar es
\[\sigma = \sqrt{\left(\dfrac{1}{p}\right)\left(\dfrac{1}{p} - 1\right)} = \sqrt{\left(\dfrac{1}{0.02}\right)\left(\dfrac{1}{0.02} - 1\right)} = 49.5\]
Ejercicio\(\PageIndex{4}\)
La probabilidad de una varilla de acero defectuosa es de 0.01. Las varillas de acero se seleccionan al azar. Encuentra la probabilidad de que el primer defecto ocurra en la novena varilla de acero. Usa la calculadora TI-83+ o TI-84 para encontrar la respuesta.
Responder
\(P(x = 9) = 0.0092\)
Ejemplo\(\PageIndex{5}\)
El riesgo de por vida de desarrollar cáncer de páncreas es aproximadamente uno de cada 78 (1.28%). Deja que\(X =\) el número de personas que preguntes hasta que una diga que tiene cáncer de páncreas. Entonces\(X\) es una variable aleatoria discreta con una distribución geométrica:\(X \sim G\left(\dfrac{1}{78}\right)\) o\(X \sim G(0.0128)\).
- ¿Cuál es la probabilidad de que le preguntes a diez personas antes de que una diga que tiene cáncer de páncreas?
- ¿Cuál es la probabilidad de que debas preguntar a 20 personas?
- Encontrar la (i) media y (ii) desviación estándar de\(X\).
Responder
- \(P(x = 10) = \text{geometpdf}(0.0128, 10) = 0.0114\)
- \(P(x = 20) = \text{geometpdf}(0.0128, 20) = 0.01\)
-
- Media\(= \mu = \dfrac{1}{p} = \dfrac{1}{0.0128} = 78\)
- Desviación estándar\(= \sigma = \sqrt{\dfrac{1-p}{p^{2}}} = \sqrt{\dfrac{1-0.0128}{0.0128^{2}}} \approx 77.6234\)
Ejercicio\(\PageIndex{5}\)
La tasa de alfabetización de una nación mide la proporción de personas mayores de 15 años que pueden leer y escribir. La tasa de alfabetización de las mujeres en Afganistán es de 12%. Deja que\(X =\) el número de mujeres afganas que pidas hasta que una diga que está alfabetizada.
- ¿Cuál es la distribución de probabilidad\(X\)?
- ¿Cuál es la probabilidad de que le preguntes a cinco mujeres antes de que una diga que está alfabetizada?
- ¿Cuál es la probabilidad de que debas preguntar a diez mujeres?
- Encontrar la (i) media y (ii) desviación estándar de\(X\).
Responder
- \(X \sim G(0.12)\)
- \(P(x = 5) = \text{geometpdf}(0.12, 5) = 0.0720\)
- \(P(x = 10) = \text{geometpdf}(0.12, 10) = 0.0380\)
-
- Media\(= \mu = \dfrac{1}{p} = \dfrac{1}{0.12} \approx 3333\)
- Desviación estándar\(= \sigma = \dfrac{1-p}{p^{2}} = \dfrac{1-0.12}{0.12^{2}} \approx 7.8174\)
Referencias
- “Millennials: Un retrato de la siguiente generación”, PewResearchCenter. Disponible en línea en www.pewsocialtrends.org/files... -to-change.pdf (consultado el 15 de mayo de 2013).
- “Millennials: Confiados. Conectado. Abierto al Cambio”. Resumen Ejecutivo por PewResearch Social & Demographic Trends, 2013. Disponible en línea en http://www.pewsocialtrends.org/2010/...pen-to-change/ (consultado el 15 de mayo de 2013).
- “Prevalencia del VIH, total (% de poblaciones entre 15 y 49 años)”, El Banco Mundial, 2013. Disponible en línea en http://data.worldbank.org/indicator/...last&sort=desc (consultado el 15 de mayo de 2013).
- Pryor, John H., Linda DeAngelo, Laura Palucki Blake, Sylvia Hurtado, Serge Tran. The American Freshman: Normas Nacionales Otoño 2011. Los Ángeles: Programa de Investigación Institucional Cooperativa en el Instituto de Investigación en Educación Superior de la UCLA, 2011. También disponible en línea en http://heri.ucla.edu/PDFs/pubs/TFS/N...eshman2011.pdf (consultado el 15 de mayo de 2013).
- “Resumen de la Evaluación Nacional de Riesgo y Vulnerabilidad 2007/8: Un perfil de Afganistán”, La Unión Europea y el ICON-instituto. Disponible en línea en ec.europa.eu/europeaid/where/... summary_en.pdf (consultado el 15 de mayo de 2013).
- “The World FactBook”, Agencia Central de Inteligencia. Disponible en línea en https://www.cia.gov/library/publicat...k/geos/af.html (consultado el 15 de mayo de 2013).
- “UNICEF informa sobre los Centros de Alfabetización Femenina en Afganistán establecidos para enseñar a mujeres y niñas habilidades básicas de reescritura [sic] y escritura”, UNICEF Televisión. Video disponible en línea en http://www.unicefusa.org/assets/vide...y-centers.html (consultado el 15 de mayo de 2013).
Revisar
Hay tres características de un experimento geométrico:
- Hay uno o más juicios de Bernoulli con todos los fracasos excepto el último, lo cual es un éxito.
- En teoría, el número de juicios podría continuar para siempre. Debe haber al menos un juicio.
- La probabilidad,\(p\), de un éxito y la probabilidad,\(q\), de un fracaso son las mismas para cada ensayo.
En un experimento geométrico, definir la variable aleatoria discreta\(X\) como el número de ensayos independientes hasta el primer éxito. Decimos que\(X\) tiene una distribución geométrica y escribimos\(X \sim G(p)\) donde\(p\) está la probabilidad de éxito en un solo ensayo. La media de la distribución geométrica\(X \sim G(p)\) es\(\mu = \dfrac{1-p}{p^{2}} = \sqrt{\dfrac{1}{p}\left(\dfrac{1}{p} - 1\right)}\).
Revisión de Fórmula
\(X \sim G(p)\)significa que la variable aleatoria discreta\(X\) tiene una distribución geométrica de probabilidad con probabilidad de éxito en un solo ensayo\(p\).
\(X =\)el número de ensayos independientes hasta el primer éxito
\(X\)adquiere los valores\(x = 1, 2, 3, \dotsc\)
\(p =\)la probabilidad de éxito para cualquier juicio
\(q =\)la probabilidad de un fracaso para cualquier juicio\(p + q = 1\)
\(q = 1 – p\)
La media es\(\mu = \dfrac{1}{p}\).
La desviación estándar es\(\sigma = \dfrac{1-p}{p^{2}} = \sqrt{\dfrac{1}{p}\left(\dfrac{1}{p} - 1\right)}\).
Utiliza la siguiente información para responder a los siguientes seis ejercicios: El Instituto de Investigación en Educación Superior de UCLA recopiló datos de 203,967 estudiantes de primer año entrantes de tiempo completo de 270 colegios y universidades de cuatro años en Estados Unidos. El 71.3% de esos estudiantes respondió que, sí, creen que las parejas del mismo sexo deben tener derecho al estado civil legal. Supongamos que seleccionas aleatoriamente a estudiantes de primer año del estudio hasta que encuentres uno que conteste “sí”. Te interesa el número de estudiantes de primer año que debes preguntar.
Ejercicio 4.5.6
En palabras, defina la variable aleatoria\(X\).
Contestar
\(X =\)el número de estudiantes de primer año seleccionados del estudio hasta que uno contestó “sí” que las parejas del mismo sexo deberían tener derecho al estado civil legal.
Ejercicio 4.5.7
\(X \sim\)_____ (_____, _____)
Ejercicio 4.5.8
¿Qué valores adquiere la\(X\) variable aleatoria?
Contestar
1,2,...
Ejercicio 4.5.9
Construir la función de distribución de probabilidad (PDF). Deténgase en\(x = 6\).
| \(x\) | \(P(x)\) |
|---|---|
| \ (x\) ">1 | \ (P (x)\) "> |
| \ (x\) ">2 | \ (P (x)\) "> |
| \ (x\) ">3 | \ (P (x)\) "> |
| \ (x\) ">4 | \ (P (x)\) "> |
| \ (x\) ">5 | \ (P (x)\) "> |
| \ (x\) ">6 | \ (P (x)\) "> |
Ejercicio 4.5.10
En promedio (\(\mu\)), ¿cuántos estudiantes de primer año esperarías tener que preguntar hasta que encuentres uno que conteste “sí?”
Contestar
1.4
Ejercicio 4.5.11
¿Cuál es la probabilidad de que necesites preguntar a menos de tres estudiantes de primer año?
Notas al pie
1” Prevalencia del VIH, total (% de poblaciones entre 15 y 49 años)” El Banco Mundial, 2013. Disponible en línea en http://data.worldbank.org/indicator/...pi_data_value - last&sort=desc (consultado el 15 de mayo de 2013).
Glosario
- Distribución Geométrica
- una variable aleatoria discreta (RV) que surge de los ensayos de Bernoulli; los ensayos se repiten hasta el primer éxito. La variable geométrica\(X\) se define como el número de ensayos hasta el primer éxito. Notación:\(X \sim G(p)\). La media es\(\mu = \dfrac{1}{p}\) y la desviación estándar es\(\sigma =\)
-
\[\sqrt{\dfrac{1}{p}\left(\dfrac{1}{p} - 1\right)}\]
- . La probabilidad de\(x\) fracasos exactos antes del primer éxito viene dada por la fórmula:\(P(X = x) = p(1 –p)^{x-1}\).
- Experimento Geométrico
- un experimento estadístico con las siguientes propiedades:
-
- Hay uno o más juicios de Bernoulli con todos los fracasos excepto el último, lo cual es un éxito.
- En teoría, el número de juicios podría continuar para siempre. Debe haber al menos un juicio.
- La probabilidad,\(p\), de un éxito y la probabilidad,\(q\), de un fracaso no cambian de un juicio a otro.


