5.3: La distribución uniforme

Última actualización
Guardar como PDF

Page ID: 153269

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

La distribución uniforme es una distribución de probabilidad continua y se refiere a eventos que son igualmente probables de ocurrir. Al resolver problemas que tengan una distribución uniforme, tenga cuidado de anotar si los datos son inclusivos o exclusivos.

Ejemplo 5.3.1

Los datos en la Tabla\(\PageIndex{1}\) son 55 tiempos de sonrisa, en segundos, de un bebé de ocho semanas de edad.

Mesa\(\PageIndex{1}\)
10.4	19.6	18.8	13.9	17.8	16.8	21.6	17.9	12.5	11.1	4.9
12.8	14.8	22.8	20.0	15.9	16.3	13.4	17.1	14.5	19.0	22.8
1.3	0.7	8.9	11.9	10.9	7.3	5.9	3.7	17.9	19.2	9.8
5.8	6.9	2.6	5.8	21.7	11.8	3.4	2.1	4.5	6.3	10.7
8.9	9.4	9.4	7.6	10.0	3.3	6.7	7.8	11.6	13.8	18.6

La media muestral = 11.49 y la desviación estándar muestral = 6.23.

Supondremos que los tiempos de sonreír, en segundos, siguen una distribución uniforme entre cero y 23 segundos, inclusive. Esto significa que cualquier tiempo de sonreír de cero a e incluyendo 23 segundos es igualmente probable. El histograma que se podría construir a partir de la muestra es una distribución empírica que coincide estrechamente con la distribución uniforme teórica.

Dejar\(X =\) alargar, en segundos, de la sonrisa de un bebé de ocho semanas.

La notación para la distribución uniforme es

\(X \sim U(a, b)\)donde\(a =\) el valor más bajo de\(x\) y\(b =\) el valor más alto de\(x\).

La función de densidad de probabilidad es\(f(x) = \frac{1}{b-a}\) para\(a \leq x \leq b\).

Para este ejemplo,\(X \sim U(0, 23)\) y\(f(x) = \frac{1}{23-0}\) para\(0 \leq X \leq 23\).

Las fórmulas para la media teórica y la desviación estándar son

\[\mu = \frac{a+b}{2} \nonumber\]

\[\sigma = \sqrt{\frac{(b-a)^{2}}{12}} \nonumber\]

Para este problema, la media teórica y la desviación estándar son

\[\mu = \frac{0+23}{2} = 11.50 \, seconds \nonumber\]

\[\sigma = \frac{(23-0)^{2}}{12} = 6.64\, seconds. \nonumber\]

Observe que la media teórica y la desviación estándar están cerca de la media y desviación estándar de la muestra en este ejemplo.

Ejercicio\(\PageIndex{1}\)

Los datos que siguen son el número de pasajeros en 35 diferentes barcos de pesca chárter. La media muestral = 7.9 y la desviación estándar muestral = 4.33. Los datos siguen una distribución uniforme donde todos los valores entre e incluyendo cero y 14 son igualmente probables. Indicar los valores de a y\(b\). Escribir la distribución en notación apropiada, y calcular la media teórica y la desviación estándar.

Mesa\(\PageIndex{2}\)
1	12	4	10	4	14	11
7	11	4	13	2	4	6
3	10	0	12	6	9	10
5	13	4	10	14	12	11
6	10	11	0	11	13	2

Responder

\(a\)es cero;\(b\) es\(14\);\(X \sim U (0, 14)\);\(\mu = 7\) pasajeros;\(\sigma = 4.04\) pasajeros

Ejemplo 5.3.2A

a. Consulte el Ejemplo 5.3.1. ¿Cuál es la probabilidad de que un bebé de ocho semanas elegido al azar sonríe entre dos y 18 segundos?

Responder

a. Encontrar\(P(2 < x < 18)\).

\(P(2 < x < 18) = (\text{base})(\text{height}) = (18 – 2)\left(\frac{1}{23}\right) = \left(\frac{16}{23}\right)\).

Esta gráfica muestra una distribución uniforme. El eje horizontal oscila entre 0 y 15. La distribución es modelada por un rectángulo que se extiende de x = 0 a x = 15. Una región de x = 2 a x = 18 está sombreada dentro del rectángulo. — Figura\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)B

b. Encontrar el ^percentil 90 para el momento de sonreír de un bebé de ocho semanas.

Responder

b. el noventa por ciento de los tiempos de sonreír caen por debajo del ^percentil 90,\(k\), entonces\(P(x < k) = 0.90\)

\[P(x < k)= 0.90\]

\[(\text{base})(\text{height}) = 0.90\]

\[(k−0)\left(\frac{1}{23}\right) = 0.90\]

\[k = (23)(0.90) = 20.7\]

Esto muestra la gráfica de la función f (x) = 1/15. Una línea horizontal va desde el punto (0, 1/15) hasta el punto (15, 1/15). Una línea vertical se extiende desde el eje x hasta el final de la línea en el punto (15, 1/15) creando un rectángulo. Una región se sombrea dentro del rectángulo de x = 0 a x = k; el área sombreada representa P (x < k) = 0.90. — Figura\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)C

c. Encuentra la probabilidad de que un bebé aleatorio de ocho semanas sonríe más de 12 segundos SABIENDO que el bebé sonríe MÁS DE OCHO SEGUNDOS.

Responder

c. Esta pregunta de probabilidad es condicional. Se te pide que encuentres la probabilidad de que un bebé de ocho semanas sonríe más de 12 segundos cuando ya sabes que el bebé ha sonreído por más de ocho segundos.

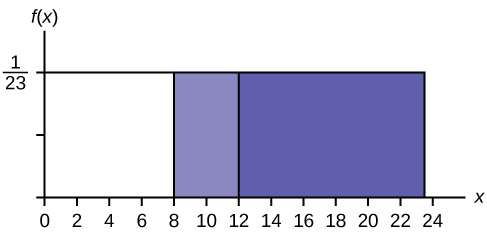
Encuentra\(P(x > 12 | x > 8)\) Hay dos formas de hacer el problema. Para la primera forma, usa el hecho de que se trata de un condicional y cambia el espacio muestral. La gráfica ilustra el nuevo espacio muestral. Ya sabes que el bebé sonrió más de ocho segundos.

Escribe un nuevo\(f(x): f(x) = \frac{1}{23-8} = \frac{1}{15}\)

para\(8 < x < 23\)

\(P(x > 12 | x > 8) = (23 − 12)\left(\frac{1}{15}\right) = \left(\frac{11}{15}\right)\)

f (X) =1/15 gráfica que muestra una región en caja que consiste en una línea horizontal que se extiende hacia la derecha desde el punto 1/15 en el eje y, una línea vertical hacia arriba desde los puntos 8 y 23 en el eje x, y el eje x. Una región sombreada desde los puntos 12-23 ocurre dentro de esta área. — Figura\(\PageIndex{3}\)

Para la segunda forma, use la fórmula condicional de Probability Topics con la distribución original\(X \sim U(0, 23)\):

\(P(\text{A|B}) = \frac{P(\text{A AND B})}{P(\text{B})}\)

Para este problema,\(\text{A}\) is (\(x > 12\)) y\(\text{B}\) is (\(x > 8\)).

Entonces,\(P(x > 12|x > 8) = \frac{(x > 12 \text{ AND } x > 8)}{P(x > 8)} = \frac{P(x > 12)}{P(x > 8)} = \frac{\frac{11}{23}}{\frac{15}{23}} = \frac{11}{15}\)

Figura\(\PageIndex{4}\): El área sombreada más oscura representa\(P(x > 12)\). Se muestra toda el área sombreada\(P(x > 8)\).

Ejercicio\(\PageIndex{2}\)

Una distribución se da como\(X \sim U(0, 20)\). ¿Qué es\(P(2 < x < 18)\)? Encuentra el ^percentil 90.

Responder

\(P(2 < x < 18) = 0.8\); ^percentil 90\(= 18\)

Ejemplo 5.3.3

La cantidad de tiempo, en minutos, que una persona debe esperar un autobús se distribuye uniformemente entre cero y 15 minutos, inclusive.

Ejercicio\(\PageIndex{3}\).1

a. ¿Cuál es la probabilidad de que una persona espere menos de 12.5 minutos?

Responder

a. dejar\(X =\) el número de minutos que una persona debe esperar por un autobús. \(a = 0\)y\(b = 15\). \(X \sim U(0, 15)\). Escribe la función de densidad de probabilidad. \(f(x) = \frac{1}{15-0} = \frac{1}{15}\)para\(0 \leq x \leq 15\).

Encontrar\(P(x < 12.5)\). Dibuja una gráfica.

\[P(x < k) = (\text{base})(\text{height}) = (12.5−0)\left(\frac{1}{15}\right) = 0.8333\]

La probabilidad de que una persona espere menos de 12.5 minutos es de 0.8333.

Ejercicio\(\PageIndex{3}\).2

b. En promedio, ¿cuánto tiempo debe esperar una persona? Encuentra la media,\(\mu\), y la desviación estándar,\(\sigma\).

Responder

b\(\mu = \frac{a+b}{2} = \frac{15+0}{2} = 7.5\). En promedio, una persona debe esperar 7.5 minutos.

\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}} = \sqrt{\frac{(12-0)^{2}}{12}} = 4.3\). La desviación estándar es de 4.3 minutos.

Ejercicio\(\PageIndex{3}\).3

c. ¿Noventa por ciento del tiempo, el tiempo que una persona debe esperar cae por debajo de qué valor?

Nota 5.3.3.3.1

Esto pide el ^percentil 90.

Responder

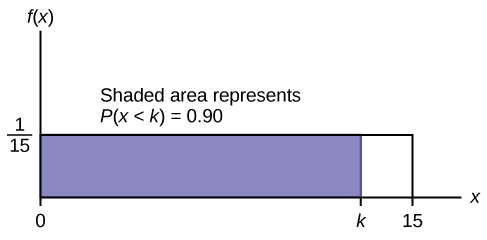
c. Encuentra el ^percentil 90. Dibuja una gráfica. Dejemos que\(k =\) el ^percentil 90.

\(P(x < k) = (\text{base})(\text{height}) = (k−0)\left(\frac{1}{15}\right)\)
\(0.90 = (k)\left(\frac{1}{15}\right)\)
\(k = (0.90)(15) = 13.5\)
\(k\)a veces se llama un valor crítico.
El ^percentil 90 es de 13.5 minutos. El noventa por ciento del tiempo, una persona debe esperar como máximo 13.5 minutos.

Ejercicio\(\PageIndex{4}\)

La duración total de los juegos de beisbol en las Grandes Ligas en la temporada 2011 se distribuye uniformemente entre 447 horas y 521 horas inclusive.

Encontrar\(a\)\(b\) y describir lo que representan.
Escribe la distribución.
Encuentra la media y la desviación estándar.
¿Cuál es la probabilidad de que la duración de los juegos para un equipo para la temporada 2011 sea entre 480 y 500 horas?
¿Cuál es el ^percentil 65 por la duración de los juegos para un equipo para la temporada 2011?

Responder

\(a\)es\(447\), y\(b\) es\(521\). a es la duración mínima de juegos para un equipo para la temporada 2011, y\(b\) es la duración máxima de juegos para un equipo para la temporada 2011.
\(X \sim U(447, 521)\).
\(\mu = 484\), y\(\sigma = 21.36\)

Figura\(\PageIndex{1}\).
\(P(480 < x < 500) = 0.2703\)
El ^percentil 65 es de 495.1 horas.

Ejemplo 5.3.4

Supongamos que el tiempo que tarda un niño de nueve años en comer una rosquilla es entre 0.5 y 4 minutos, inclusive. Que\(X =\) el tiempo, en minutos, le toma a un niño de nueve años comer una rosquilla. Entonces\(X \sim U(0.5, 4)\).

a. La probabilidad de que un niño de nueve años seleccionado al azar coma una rosquilla en al menos dos minutos es _______.

Solución

a. 0.5714

Ejercicio\(\PageIndex{4}\).1

b. encontrar la probabilidad de que otro niño de nueve años se coma una rosquilla en más de dos minutos dado que el niño ya ha estado comiendo la rosquilla por más de 1.5 minutos.

La segunda pregunta tiene una probabilidad condicional. Se le pide que encuentre la probabilidad de que un niño de nueve años se coma una rosquilla en más de dos minutos dado que el niño ya lleva más de 1.5 minutos comiendo la rosquilla. Resolver el problema de dos maneras diferentes (ver Ejemplo). Debe reducir el espacio muestral. Primera forma: Como sabes que el niño ya lleva más de 1.5 minutos comiendo la rosquilla, ya no estás comenzando a = 0.5 minutos. Su punto de partida es de 1.5 minutos.

Escribe un nuevo\(f(x)\):

\(f(x) = \frac{1}{4-1.5} = \frac{2}{5}\)para\(1.5 \leq x \leq 4\).

Encontrar\(P(x > 2|x > 1.5)\). Dibuja una gráfica.

f (X) =2/5 gráfica que muestra una región en caja que consiste en una línea horizontal que se extiende hacia la derecha desde el punto 2/5 en el eje y, una línea vertical hacia arriba desde los puntos 1.5 y 4 en el eje x, y el eje x. Una región sombreada desde los puntos 2-4 ocurre dentro de esta área. — Figura\(\PageIndex{2}\).

\(P(x > 2|x > 1.5) = (\text{base})(\text{new height}) = (4 − 2)(25)\left(\frac{2}{5}\right) =\)?

Responder

b.\(\frac{4}{5}\)

La probabilidad de que un niño de nueve años se coma una rosquilla en más de dos minutos dado que el niño ya lleva más de 1.5 minutos comiendo la rosquilla es\(\frac{4}{5}\).

Segunda forma: Dibuja la gráfica original para\(X \sim U(0.5, 4)\). Usar la fórmula condicional

\(P(x > 2 | x > 1.5) = \frac{P(x > 2 \text{AND} x > 1.5)}{P(x > 1.5)} = \frac{P(x>2)}{P(x>1.5)} = \frac{\frac{2}{3.5}}{\frac{2.5}{3.5}} = 0.8 = \frac{4}{5}\)

Ejercicio\(\PageIndex{5}\)

Supongamos que el tiempo que tarda un alumno en terminar un cuestionario se distribuye uniformemente entre seis y 15 minutos, inclusive. Deje que\(X =\) el tiempo, en minutos, le lleve a un alumno terminar un cuestionario. Entonces\(X \sim U(6, 15)\).

Encuentra la probabilidad de que un estudiante seleccionado al azar necesite al menos ocho minutos para completar el cuestionario. Entonces encuentra la probabilidad de que un estudiante diferente necesite al menos ocho minutos para terminar el cuestionario dado que ya ha tardado más de siete minutos.

Responder

\(P(x > 8) = 0.7778\)

\(P(x > 8 | x > 7) = 0.875\)

Ejemplo 5.3.5

Ace Heating and Air Conditioning Service encuentra que la cantidad de tiempo que un reparador necesita para reparar un horno se distribuye uniformemente entre 1.5 y cuatro horas. Deje que\(x =\) el tiempo necesario para arreglar un horno. Entonces\(x \sim U(1.5, 4)\).

Encuentre la probabilidad de que una reparación de horno seleccionada aleatoriamente requiera más de dos horas.
Encuentre la probabilidad de que una reparación de horno seleccionada aleatoriamente requiera menos de tres horas.
Encuentre el ^percentil 30 de los tiempos de reparación del horno.
¿El 25% más largo de los tiempos de reparación del horno tardan al menos en cuánto tiempo? (En otras palabras: encontrar el tiempo mínimo para el 25% de los tiempos de reparación más largos.) ¿Qué percentil representa esto?
Encuentra la media y la desviación estándar

Solución

a. Para\(f(x): f(x) = \frac{1}{4-1.5} = \frac{1}{2.5}\) encontrarla\(f(x) = 0.4\)

\(P(x > 2) = (\text{base})(\text{height}) = (4 – 2)(0.4) = 0.8\)

Esto muestra la gráfica de la función f (x) = 0.4. Una línea horizontal va desde el punto (1.5, 0.4) hasta el punto (4, 0.4). Las líneas verticales se extienden desde el eje x hasta la gráfica en x = 1.5 y x = 4 creando un rectángulo. Una región está sombreada dentro del rectángulo de x = 2 a x = 4. — Figura\(\PageIndex{3}\). Distribución uniforme entre 1.5 y cuatro con área sombreada entre dos y cuatro que representa la probabilidad de que el tiempo de reparación\(x\) sea mayor que dos

b.\(P(x < 3) = (\text{base})(\text{height}) = (3 – 1.5)(0.4) = 0.6\)

La gráfica del rectángulo que muestra toda la distribución permanecería igual. Sin embargo, la gráfica debe estar sombreada entre\(x = 1.5\) y\(x = 3\). Tenga en cuenta que el área sombreada comienza en\(x = 1.5\) lugar de en\(x = 0\); ya que\(X \sim U(1.5, 4)\), no\(x\) puede ser inferior a 1.5.

\(P(x < k) = 0.30\)
\(P(x < k) = (\text{base})(\text{height}) = (k – 1.5)(0.4)\)
\(0.3 = (k – 1.5) (0.4)\); Resolver para encontrar\(k\):
\(0.75 = k – 1.5\), obtenido dividiendo ambos lados por 0.4
\(k = 2.25\), obtenido sumando 1.5 a ambos lados

El ^percentil 30 de los tiempos de reparación es de 2.25 horas. El 30% de los tiempos de reparación son de 2.25 horas o menos.

Figura\(\PageIndex{6}\). Distribución uniforme entre 1.5 y 4 con un área de 0.25 sombreada a la derecha que representa el 25% más largo de los tiempos de reparación.

\(P(x > k) = 0.25\)
\(P(x > k) = (\text{base})(\text{height}) = (4 – k)(0.4)\)
\(0.25 = (4 – k)(0.4)\); Resolver para\(k\):
\(0.625 = 4 − k\),
obtenido dividiendo ambos lados por 0.4
\(−3.375 = −k\),
obtenido restando cuatro de ambos lados: \(k = 3.375\)
El 25% más largo de las reparaciones del horno tardan al menos 3.375 horas (3.375 horas o más).

Nota: Dado que el 25% de los tiempos de reparación son de 3.375 horas o más, eso significa que el 75% de los tiempos de reparación son de 3.375 horas o menos. 3.375 horas es el ^percentil 75 de los tiempos de reparación del horno.

e.\(\mu = \frac{a+b}{2}\) y\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\)

\(\mu = \frac{1.5+4}{2} = 2.75\)horas y\(\sigma = \sqrt{\frac{(4-1.5)^{2}}{12}} = 0.7217\) horas

Ejercicio\(\PageIndex{6}\)

La cantidad de tiempo que un técnico de servicio necesita para cambiar el aceite en un automóvil se distribuye uniformemente entre 11 y 21 minutos. Deje que\(X =\) el tiempo necesario para cambiar el aceite en un automóvil.

Escribe la variable aleatoria\(X\) en palabras. \(X =\)__________________.
Escribe la distribución.
Grafica la distribución.
Encontrar\(P(x > 19)\).
Encuentra el ^percentil 50.

Responder

Deje que\(X =\) el tiempo necesario para cambiar el aceite en un automóvil.
\(X \sim U(11, 21)\).
Figura\(\PageIndex{7}\).
\(P(x > 19) = 0.2\)
el ^percentil 50 es de 16 minutos.

Revisar

Si\(X\) tiene una distribución uniforme donde\(a < x < b\) o\(a \leq x \leq b\), luego\(X\) toma valores entre\(a\) y\(b\) (puede incluir\(a\) y\(b\)). Todos los valores\(x\) son igualmente probables. Escribimos\(X \sim U(a, b)\). La media de\(X\) es\(\mu = \frac{a+b}{2}\). La desviación estándar de\(X\) es\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\). La función de densidad de probabilidad de\(X\) es\(f(x) = \frac{1}{b-a}\) para\(a \leq x \leq b\). La función de distribución acumulativa de\(X\) es\(P(X \leq x) = \frac{x-a}{b-a}\). \(X\)es continuo.

La gráfica muestra un rectángulo con área total igual a 1. El rectángulo se extiende de x = a x = b en el eje x y tiene una altura de 1/ (b-a). — Figura\(\PageIndex{8}\).

La probabilidad se\(P(c < X < d)\) puede encontrar calculando el área bajo\(f(x)\), entre\(c\) y\(d\). Dado que el área correspondiente es un rectángulo, el área se puede encontrar simplemente multiplicando el ancho y la altura.

Revisión de Fórmula

\(X =\)un número real entre\(a\) y\(b\) (en algunos casos,\(X\) puede tomar los valores\(a\) y\(b\)). \(a =\)más pequeño\(X\);\(b =\) más grande\(X\)

\(X \sim U(a, b)\)

La media es\(\mu = \frac{a+b}{2}\)

La desviación estándar es\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\)

Función de densidad de probabilidad:\(f(x) = \frac{1}{b-a} \text{for} a \leq X \leq b\)

Área a la izquierda de\(x\):\(P(X < x) = (x – a)\left(\frac{1}{b-a}\right)\)

Área a la derecha de\(x\): P (\(X\)>\(x\)) = (b — x)\(\left(\frac{1}{b-a}\right)\)

Área entre\(c\) y\(d\):\(P(c < x < d) = (\text{base})(\text{height}) = (d – c)\left(\frac{1}{b-a}\right)\)

Uniforme:\(X \sim U(a, b)\) donde\(a < x < b\)

pdf:\(f(x) = \frac{1}{b-a}\) para\(a \leq x \leq b\)
cdf:\(P(X \leq x) = \frac{x-a}{b-a}\)
media\(\mu = \frac{a+b}{2}\)
desviación estándar\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\)
\(P(c < X < d) = (d – c)\left(\frac{1}{b-a}\right)\)

Referencias

McDougall, John A. El Programa McDougall para la Pérdida Máxima de Peso. Penacho, 1995.

Utilice la siguiente información para responder a las siguientes diez preguntas. Los datos que siguen son los pies cuadrados (en 1,000 pies cuadrados) de 28 viviendas.

1.5	2.4	3.6	2.6	1.6	2.4	2.0
3.5	2.5	1.8	2.4	2.5	3.5	4.0
2.6	1.6	2.2	1.8	3.8	2.5	1.5
2.8	1.8	4.5	1.9	1.9	3.1	1.6

La media muestral = 2.50 y la desviación estándar de la muestra = 0.8302.

La distribución se puede escribir como\(X \sim U(1.5, 4.5)\).

Ejercicio\(\PageIndex{7}\)

¿Qué tipo de distribución es esta?

Ejercicio\(\PageIndex{8}\)

En esta distribución, los resultados son igualmente probables. ¿Qué significa esto?

Responder

Significa que el valor de x es igual de probable que sea cualquier número entre 1.5 y 4.5.

Ejercicio\(\PageIndex{9}\)

¿Cuál es la altura de\(f(x)\) para la distribución continua de probabilidad?

Ejercicio\(\PageIndex{10}\)

¿Cuáles son las limitaciones para los valores de\(x\)?

Responder

\(1.5 \leq x \leq 4.5\)

Ejercicio\(\PageIndex{11}\)

Gráfica\(P(2 < x < 3)\).

Ejercicio\(\PageIndex{12}\)

¿Qué es\(P(2 < x < 3)\)?

Responder

0.3333

Ejercicio\(\PageIndex{13}\)

¿Qué es\(P(x < 3.5 | x < 4)\)?

Ejercicio\(\PageIndex{14}\)

¿Qué es\(P(x = 1.5)\)?

Responder

cero

Ejercicio\(\PageIndex{15}\)

¿Cuál es el ^percentil 90 de pies cuadrados para los hogares?

Ejercicio\(\PageIndex{16}\)

Encuentra la probabilidad de que una casa seleccionada al azar tenga más de 3,000 pies cuadrados dado que ya sabes que la casa tiene más de 2,000 pies cuadrados.

Responder

0.6

Ejercicio\(\PageIndex{17}\)

¿Qué es\(a\)? ¿Qué representa?

Ejercicio\(\PageIndex{18}\)

¿Qué es\(b\)? ¿Qué representa?

Responder

\(b\)es\(12\), y representa el valor más alto de\(x\).

Ejercicio\(\PageIndex{19}\)

¿Cuál es la función de densidad de probabilidad?

Ejercicio\(\PageIndex{20}\)

¿Cuál es la media teórica?

Responder

seis

Ejercicio\(\PageIndex{21}\)

¿Cuál es la desviación estándar teórica?

Ejercicio\(\PageIndex{22}\)

Dibuja la gráfica de la distribución para\(P(x > 9)\).

Responder

Esta gráfica muestra una distribución uniforme. El eje horizontal oscila entre 0 y 12. La distribución es modelada por un rectángulo que se extiende de x = 0 a x = 12. Una región de x = 9 a x = 12 está sombreada dentro del rectángulo. — Figura\(\PageIndex{9}\).

Ejercicio\(\PageIndex{23}\)

Encontrar\(P(x > 9)\).

Ejercicio\(\PageIndex{24}\)

Encuentra el ^percentil 40.

Responder

4.8

Utilice la siguiente información para responder a los siguientes once ejercicios. La antigüedad de los autos en el estacionamiento del personal de un colegio suburbano se distribuye uniformemente de seis meses (0.5 años) a 9.5 años.

Ejercicio\(\PageIndex{25}\)

¿Qué se está midiendo aquí?

Ejercicio\(\PageIndex{26}\)

En palabras, defina la variable aleatoria\(X\).

Responder

\(X\)= La edad (en años) de los autos en el estacionamiento del personal

Ejercicio\(\PageIndex{27}\)

¿Los datos son discretos o continuos?

Ejercicio\(\PageIndex{28}\)

El intervalo de valores para\(x\) es ______.

Contestar

0.5 a 9.5

Ejercicio\(\PageIndex{29}\)

La distribución para\(X\) es ______.

Ejercicio\(\PageIndex{30}\)

Escribe la función de densidad de probabilidad.

Contestar

\(f(x) = \frac{1}{9}\)donde\(x\) está entre 0.5 y 9.5, inclusive.

Ejercicio\(\PageIndex{31}\)

Grafica la distribución de probabilidad.

Esbozar la gráfica de la distribución de probabilidad.

Figura\(\PageIndex{10}\).
Identificar los siguientes valores:
1. Valor más bajo para\(\bar{x}\): _______
2. Valor más alto para\(\bar{x}\): _______
3. Altura del rectángulo: _______
4. Etiqueta para el eje x (palabras): _______
5. Etiqueta para eje y (palabras): _______

Ejercicio\(\PageIndex{32}\)

Encuentra la edad promedio de los autos en el lote.

Contestar

\(\mu\)= 5

Ejercicio\(\PageIndex{33}\)

Encuentra la probabilidad de que un auto elegido al azar en el lote tuviera menos de cuatro años de antigüedad.

Dibuje la gráfica y sombree el área de interés.

Figura\(\PageIndex{11}\).
Encuentra la probabilidad. \(P(x < 4) =\)_______

Ejercicio\(\PageIndex{34}\)

Considerando solo los autos de menos de 7.5 años de antigüedad, encuentra la probabilidad de que un auto elegido al azar en el lote tuviera menos de cuatro años de antigüedad.

Dibuje la gráfica, sombree el área de interés.

Figura\(\PageIndex{12}\).
Encuentra la probabilidad. \(P(x < 4 | x < 7.5) =\)_______

Contestar

Consulta la solución del alumno.
\(\frac{3.5}{7}\)

Ejercicio\(\PageIndex{35}\)

Qué ha cambiado en los dos problemas anteriores que hicieron diferentes las soluciones

Ejercicio\(\PageIndex{36}\)

Encuentra el tercer cuartil de edades de los autos en el lote. Esto significa que tendrás que encontrar el valor de tal manera que\(\frac{3}{4}\), o 75%, de los autos sean como máximo (menores o iguales a) esa edad.

Dibuje la gráfica y sombree el área de interés.

Figura\(\PageIndex{13}\).
Encuentra el valor\(k\) tal que\(P(x < k) = 0.75\).
El tercer cuartil es _______

Contestar

Consulta la solución del alumno.
\(k = 7.25\)
\(7.25\)

Glosario

Probabilidad Condicional: la probabilidad de que ocurra un evento dado que ya se ha producido otro evento

Search

Text Color

Text Size

Margin Size

Font Type

1.5	2.4	3.6	2.6	1.6	2.4	2.0
3.5	2.5	1.8	2.4	2.5	3.5	4.0
2.6	1.6	2.2	1.8	3.8	2.5	1.5
2.8	1.8	4.5	1.9	1.9	3.1	1.6

1.5	2.4	3.6	2.6	1.6	2.4	2.0
3.5	2.5	1.8	2.4	2.5	3.5	4.0
2.6	1.6	2.2	1.8	3.8	2.5	1.5
2.8	1.8	4.5	1.9	1.9	3.1	1.6

1.5	2.4	3.6	2.6	1.6	2.4	2.0
3.5	2.5	1.8	2.4	2.5	3.5	4.0
2.6	1.6	2.2	1.8	3.8	2.5	1.5
2.8	1.8	4.5	1.9	1.9	3.1	1.6