10.2: Dos medias poblacionales con desviaciones estándar desconocidas
- Page ID
- 153319
- Las dos muestras independientes son simples muestras aleatorias de dos poblaciones distintas.
- Para las dos poblaciones distintas:
- si los tamaños de muestra son pequeños, las distribuciones son importantes (deben ser normales)
- si los tamaños de muestra son grandes, las distribuciones no son importantes (no es necesario que sean normales)
La prueba que compara dos medias poblacionales independientes con desviaciones estándar de población desconocidas y posiblemente desiguales se denomina\(t\) prueba de Aspin-Welch. La fórmula de grados de libertad fue desarrollada por Aspin-Welch.
La comparación de dos medias poblacionales es muy común. La diferencia entre las dos muestras depende tanto de las medias como de las desviaciones estándar. Medios muy diferentes pueden ocurrir por casualidad si hay una gran variación entre las muestras individuales. Para dar cuenta de la variación, tomamos la diferencia de las medias de la muestra\(\bar{X}_{1} - \bar{X}_{2}\), y dividimos por el error estándar para estandarizar la diferencia. El resultado es un estadístico de prueba de puntaje t.
Debido a que no conocemos las desviaciones estándar de la población, las estimamos utilizando las dos desviaciones estándar de la muestra de nuestras muestras independientes. Para la prueba de hipótesis, se calcula la desviación estándar estimada, o error estándar, de la diferencia en las medias de la muestra,\(\bar{X}_{1} - \bar{X}_{2}\).
El error estándar es:
\[\sqrt{\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}}\]
El estadístico de prueba (t -score) se calcula de la siguiente manera:
\[\dfrac{(\bar{x}-\bar{x}) - (\mu_{1} - \mu_{2})}{\sqrt{\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}}}\]
donde:
- \(s_{1}\)y\(s_{2}\), las desviaciones estándar de la muestra, son estimaciones de\(\sigma_{1}\) y\(\sigma_{1}\), respectivamente.
- \(\sigma_{1}\)y\(\sigma_{2}\) son las desviaciones estándar poblacionales desconocidas.
- \(\bar{x}_{1}\)y\(\bar{x}_{2}\) son las medias de la muestra. \(\mu_{1}\)y\(\mu_{2}\) son los medios poblacionales.
El número de grados de libertad (\(df\)) requiere de un cálculo algo complicado. Sin embargo, una computadora o calculadora lo calcula fácilmente. \(df\)Los no siempre son un número entero. El estadístico de prueba calculado previamente se aproxima por la t -distribución de Student con\(df\) lo siguiente:
Grados de libertad
\[df = \dfrac{\left(\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}{\left(\dfrac{1}{n_{1}-1}\right)\left(\dfrac{(s_{1})^{2}}{n_{1}}\right)^{2} + \left(\dfrac{1}{n_{2}-1}\right)\left(\dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}\]
Cuando ambos tamaños de muestra\(n_{1}\) y\(n_{2}\) son cinco o mayores, la aproximación t de Student es muy buena. Observe que las varianzas de la muestra\((s_{1})^{2}\) y no\((s_{2})^{2}\) se agrupan. (Si surge la pregunta, no acumule las varianzas.)
No es necesario computar los grados de libertad a mano. Una calculadora o computadora lo computa fácilmente.
Ejemplo\(\PageIndex{1}\): Independent groups
Se cree que la cantidad promedio de tiempo que niños y niñas de siete a 11 años pasan practicando deportes cada día es lo mismo. Se realiza un estudio y se recogen los datos, dando como resultado los datos en la Tabla\(\PageIndex{1}\). Cada población tiene una distribución normal.
| Tamaño de la muestra | Promedio de horas practicando deportes por día | Desviación estándar de muestra | |
|---|---|---|---|
| Niñas | 9 | 2 | 0.8660.866 |
| Muchachos | 16 | 3.2 | 1.00 |
¿Hay alguna diferencia en la cantidad media de tiempo que niños y niñas de siete a 11 años practican deportes cada día? Prueba al nivel de significancia del 5%.
Contestar
Se desconocen las desviaciones estándar poblacionales. Que g sea el subíndice para las niñas y b sea el subíndice para los niños. Entonces,\(\mu_{g}\) es la media poblacional para las niñas y\(\mu_{b}\) es la media poblacional para los varones. Esta es una prueba de dos grupos independientes, dos medias poblacionales.
Variable aleatoria:\(\bar{X}_{g} - \bar{X}_{b} =\) diferencia en la cantidad media muestral de tiempo que niñas y niños practican deportes cada día.
- \(H_{0}: \mu_{g} = \mu_{b}\)
- \(H_{0}: \mu_{g} - \mu_{b} = 0\)
- \(H_{a}: \mu_{g} \neq \mu_{b}\)
- \(H_{a}: \mu_{g} - \mu_{b} \neq 0\)
Las palabras “lo mismo” te dicen que\(H_{0}\) tiene un “=”. Ya que no hay otras palabras para indicar\(H_{a}\), supongamos que dice “es diferente”. Esta es una prueba de dos colas.
Distribución para la prueba: Usar\(t_{df}\) donde\(df\) se calcula usando la\(df\) fórmula para grupos independientes, dos medias poblacionales. El uso de una calculadora,\(df\) es aproximadamente 18.8462. No albergue las varianzas.
Calcula el valor p usando una distribución t de Student:\(p\text{-value} = 0.0054\)
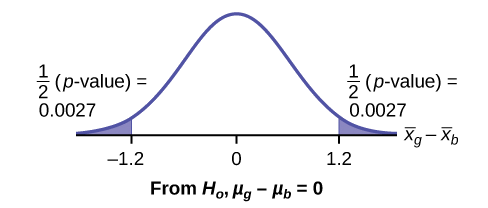
Gráfica:
\[s_{g} = 0.866\]
\[s_{b} = 1\]
Entonces,
\[\bar{x}_{g} - \bar{x}_{b} = 2 - 3.2 = -1.2\]
La mitad\(p\text{-value}\) está por debajo de —1.2 y la mitad está por encima de 1.2.
Tomar una decisión: Desde\(\alpha > p\text{-value}\), rechazar\(H_{0}\). Esto significa que rechazas\(\mu_{g} = \mu_{b}\). Los medios son diferentes.
Presione STAT. Flecha sobre PRUEBAS y presiona 4:2 -SamptTest. Flecha la flecha hacia Stats y presiona ENTRAR. Flecha hacia abajo e ingresa 2 para la media de la primera muestra,\(\sqrt{0.866}\) para Sx1, 9 para n1, 3.2 para la media de la segunda muestra, 1 para Sx2 y 16 para n2. Flecha hacia abajo a μ1: y la flecha a no es igual a μ2. Presione ENTER. Flecha hacia abajo a Agrupados: y No. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. El\(p\text{-value}\) es\(p = 0.0054\), los dfs son aproximadamente 18.8462, y el estadístico de prueba es -3.14. Vuelva a hacer el procedimiento pero en vez de Calcular hacer Dibujar.
Conclusión: En el nivel de significancia del 5%, los datos de la muestra muestran que hay evidencia suficiente para concluir que el número medio de horas que niñas y niños de siete a 11 años practican deportes por día es diferente (el número medio de horas niños de siete a 11 años practican deportes por día es mayor que la media número de horas que juegan las niñas O el número medio de horas que las niñas de siete a 11 años practican deportes al día es mayor que el número medio de horas que juegan los niños).
Ejercicio\(\PageIndex{1}\)
Dos muestras se muestran en la Tabla. Ambos tienen distribuciones normales. Se piensa que los medios para las dos poblaciones son los mismos. ¿Hay alguna diferencia en los medios? Prueba al nivel de significancia del 5%.
| Tamaño de la muestra | Media de la Muestra | Desviación estándar de muestra | |
|---|---|---|---|
| Población A | 25 | 5 | 1 |
| Población B | 16 | 4.7 | 1.2 |
Contestar
El\(p\text{-value}\) es\(0.4125\), que es muy superior a 0.05, por lo que declinamos rechazar la hipótesis nula. No hay pruebas suficientes para concluir que las medias de las dos poblaciones no son las mismas.
Cuando la suma de los tamaños de muestra es mayor de\(30 (n_{1} + n_{2} > 30)\) lo que puedes usar la distribución normal para aproximar la del estudiante\(t\).
Ejemplo\(\PageIndex{2}\)
Un estudio es realizado por un grupo comunitario en dos colegios vecinos para determinar cuál egresa a los estudiantes con más clases de matemáticas. Colegio A muestrea 11 egresados. Su promedio es de cuatro clases de matemáticas con una desviación estándar de 1.5 clases de matemáticas. Colegio B toma muestras de nueve egresados. Su promedio es de 3.5 clases de matemáticas con una desviación estándar de una clase de matemáticas. El grupo comunitario considera que un estudiante que se gradúa de la universidad A ha tomado más clases de matemáticas, en promedio. Ambas poblaciones tienen una distribución normal. Prueba a un nivel de significancia de 1%. Contesta las siguientes preguntas.
- ¿Es esto una prueba de dos medias o dos proporciones?
- ¿Se conocen o desconocen las desviaciones estándar de las poblaciones?
- ¿Qué distribución utilizas para realizar la prueba?
- ¿Cuál es la variable aleatoria?
- ¿Cuáles son las hipótesis nulas y alternativas? Escribe las hipótesis nulas y alternas en palabras y en símbolos.
- ¿Esta prueba es derecha, izquierda o de dos colas?
- ¿Cuál es el\(p\text{-value}\)?
- ¿Rechazas o no rechazas la hipótesis nula?
Soluciones
- dos medios
- desconocido
- T de Student
- \(\bar{X}_{A} - \bar{X}_{B}\)
- \(H_{0}: \mu_{A} \leq \mu_{B}\)y\(H_{a}: \mu_{A} > \mu_{B}\)
-
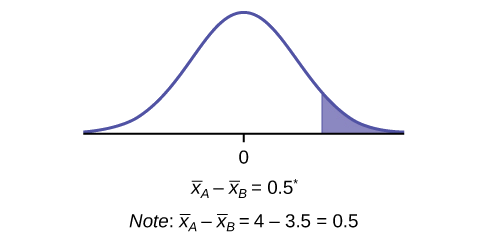
Figura\(\PageIndex{2}\).
derecha
- g. 0.1928
- h. No rechace.
- i. Al nivel de significancia del 1%, a partir de los datos de la muestra, no hay evidencia suficiente para concluir que un estudiante egresado de la universidad A haya cursado más clases de matemáticas, en promedio, que un estudiante egresado de la universidad B.
Ejercicio\(\PageIndex{2}\)
Se realiza un estudio para determinar si la Compañía A retiene a sus trabajadores por más tiempo que la Compañía B. La empresa A toma muestras de 15 trabajadores, y su tiempo promedio con la compañía es de cinco años con una desviación estándar de 1.2. La empresa B toma muestras de 20 trabajadores, y su tiempo promedio con la empresa es de 4.5 años con una desviación estándar de 0.8. Las poblaciones se distribuyen normalmente.
- ¿Se conocen las desviaciones estándar de la población?
- Realizar una prueba de hipótesis apropiada. Al nivel de significancia del 5%, ¿cuál es tu conclusión?
Contestar
- Se desconocen.
- El\(p\text{-value} = 0.0878\). Al nivel de significancia del 5%, no hay pruebas suficientes para concluir que los trabajadores de la Compañía A permanezcan más tiempo en la empresa.
Ejemplo\(\PageIndex{3}\)
Un profesor de un colegio comunitario grande quiso determinar si existe una diferencia en los medios de puntuación de los exámenes finales entre los alumnos que tomaron su curso de estadística en línea y los estudiantes que tomaron su clase presencial de estadística. Consideró que la media de los puntajes finales de los exámenes para la clase en línea sería menor que la de la clase presencial. ¿Estaba en lo correcto el profesor? Los 30 resultados de los exámenes finales seleccionados al azar de cada grupo se enumeran en Tabla\(\PageIndex{3}\) y Tabla\(\PageIndex{4}\).
| 67.6 | 41.2 | 85.3 | 55.9 | 82.4 | 91.2 | 73.5 | 94.1 | 64.7 | 64.7 |
| 70.6 | 38.2 | 61.8 | 88.2 | 70.6 | 58.8 | 91.2 | 73.5 | 82.4 | 35.5 |
| 94.1 | 88.2 | 64.7 | 55.9 | 88.2 | 97.1 | 85.3 | 61.8 | 79.4 | 79.4 |
| 77.9 | 95.3 | 81.2 | 74.1 | 98.8 | 88.2 | 85.9 | 92.9 | 87.1 | 88.2 |
| 69.4 | 57.6 | 69.4 | 67.1 | 97.6 | 85.9 | 88.2 | 91.8 | 78.8 | 71.8 |
| 98.8 | 61.2 | 92.9 | 90.6 | 97.6 | 100 | 95.3 | 83.5 | 92.9 | 89.4 |
¿La media de los puntajes del Examen Final de la clase en línea es inferior a la media de los puntajes del Examen Final de la clase presencial? Prueba a un nivel de significancia del 5%. Responde las siguientes preguntas:
- ¿Es esto una prueba de dos medias o dos proporciones?
- ¿Se conocen o desconocen las desviaciones estándar de la población?
- ¿Qué distribución utilizas para realizar la prueba?
- ¿Cuál es la variable aleatoria?
- ¿Cuáles son las hipótesis nulas y alternativas? Escribe las hipótesis nulas y alternativas en palabras y en símbolos.
- ¿Esta prueba es derecha, izquierda o de dos colas?
- ¿Cuál es el\(p\text{-value}\)?
- ¿Rechazas o no rechazas la hipótesis nula?
- En el nivel ___ de significancia, a partir de los datos de la muestra, hay ______ (es/no es) evidencia suficiente para concluir que ______.
(Ver la conclusión en Ejemplo, y escribe la tuya de manera similar)
¡Ten cuidado de no mezclar la información para el Grupo 1 y el Grupo 2!
Contestar
- dos medios
- desconocido
- Alumnos\(t\)
- \(\bar{X}_{1} - \bar{X}_{2}\)
-
- \(H_{0}: \mu_{1} = \mu_{2}\)Hipótesis nula: las medias de los puntajes finales de los exámenes son iguales para las clases de estadística online y presencial.
- \(H_{a}: \mu_{1} < \mu_{2}\)Hipótesis alternativa: la media de los puntajes finales del examen de la clase en línea es menor que la media de los puntajes finales de los exámenes de la clase presencial.
- cola izquierda
- \(p\text{-value} = 0.0011\)
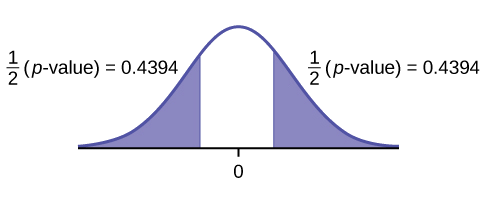
Figura\(\PageIndex{3}\).
- Rechazar la hipótesis nula
- El profesor estaba en lo correcto. La evidencia muestra que la media de los puntajes finales de los exámenes para la clase en línea es menor que la de la clase presencial.
En el nivel de significancia del 5%, a partir de los datos de la muestra, hay (es/no) evidencia suficiente para concluir que la media de los puntajes finales del examen para la clase en línea es menor que la media de los puntajes finales de los exámenes de la clase presencial.
Primero ponga los datos de cada grupo en dos listas (como L1 y L2). Presione STAT. Flecha sobre PRUEBAS y presiona 4:2 SamptTest. Asegúrese de que Data esté resaltado y presione ENTRAR. Flecha hacia abajo e ingresa L1 para la primera lista y L2 para la segunda lista. Flecha abajo a\(\mu_{1}\): y flecha a\(\neq \mu_{1}\) (no es igual). Presione ENTER. Flecha abajo a agrupados: No. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR.
Estándares de Cohen para tamaños de efecto pequeño, mediano y grande
Cohen\(d\) es una medida del tamaño del efecto basada en las diferencias entre dos medias. Cohen\(d\), llamado así por el estadístico estadounidense Jacob Cohen, mide la fuerza relativa de las diferencias entre las medias de dos poblaciones con base en los datos de la muestra. El valor calculado del tamaño del efecto se compara luego con los estándares de Cohen de tamaños de efecto pequeño, mediano y grande.
| Tamaño del efecto | \(d\) |
|---|---|
| Pequeño | \ (d\) ">0.2 |
| mediano | \ (d\) ">0.5 |
| Grande | \ (d\) ">0.8 |
Cohen\(d\) es la medida de la diferencia entre dos medias divididas por la desviación estándar agrupada:\(d = \dfrac{\bar{x}_{2}-\bar{x}_{2}}{s_{\text{pooled}}}\) donde\(s_{pooled} = \sqrt{\dfrac{(n_{1}-1)s^{2}_{1} + (n_{2}-1)s^{2}_{2}}{n_{1}+n_{2}-2}}\)
Ejemplo\(\PageIndex{4}\)
Calcular la d de Cohen para Ejemplo. ¿El tamaño del efecto es pequeño, mediano o grande? Explique qué significa el tamaño del efecto para este problema.
Contestar
\(\mu_{1} = 4 s_{1} = 1.5 n_{1} = 11\)
\(\mu_{2} = 3.5 s_{2} = 1 n_{2} = 9\)
\(d = 0.384\)
El efecto es pequeño porque 0.384 está entre el valor de Cohen de 0.2 para el tamaño del efecto pequeño y 0.5 para el tamaño del efecto medio. El tamaño de las diferencias de las medias para los dos colegios es pequeño, lo que indica que no hay una diferencia significativa entre ellos.
Ejemplo\(\PageIndex{5}\)
Calcular Cohen\(d\) por ejemplo. ¿El tamaño del efecto es pequeño, mediano o grande? Explique qué significa el tamaño del efecto para este problema.
Contestar
\(d = 0.834\); Grande, porque 0.834 es mayor que 0.8 de Cohen para un tamaño de efecto grande. El tamaño de las diferencias entre las medias de los puntajes del Examen Final de los estudiantes en línea y los estudiantes en una clase presencial es grande indicando una diferencia significativa.
Ejemplo 10.2.6
El alfa ponderado es una medida del desempeño ajustado al riesgo de las acciones durante un periodo de un año. Un alfa ponderado positivo alto significa una acción cuyo precio ha subido mientras que una pequeña alfa ponderada positiva indica un precio de acciones sin cambios durante el período de tiempo. El alfa ponderado se utiliza para identificar empresas con fuertes tendencias alcistas o bajistas. El alfa ponderado para las 30 acciones principales de bancos en el noreste y en el oeste identificadas por Nasdaq el 24 de mayo de 2013 se listan en Tabla y Tabla, respectivamente.
| 94.2 | 75.2 | 69.6 | 52.0 | 48.0 | 41.9 | 36.4 | 33.4 | 31.5 | 27.6 |
| 77.3 | 71.9 | 67.5 | 50.6 | 46.2 | 38.4 | 35.2 | 33.0 | 28.7 | 26.5 |
| 76.3 | 71.7 | 56.3 | 48.7 | 43.2 | 37.6 | 33.7 | 31.8 | 28.5 | 26.0 |
| 126.0 | 70.6 | 65.2 | 51.4 | 45.5 | 37.0 | 33.0 | 29.6 | 23.7 | 22.6 |
| 116.1 | 70.6 | 58.2 | 51.2 | 43.2 | 36.0 | 31.4 | 28.7 | 23.5 | 21.6 |
| 78.2 | 68.2 | 55.6 | 50.3 | 39.0 | 34.1 | 31.0 | 25.3 | 23.4 | 21.5 |
¿Hay alguna diferencia en el alfa ponderado de las 30 principales acciones de bancos en el noreste y en el oeste? Prueba a un nivel de significancia del 5%. Responde las siguientes preguntas:
- ¿Es esto una prueba de dos medias o dos proporciones?
- ¿Se conocen o desconocen las desviaciones estándar de la población?
- ¿Qué distribución utilizas para realizar la prueba?
- ¿Cuál es la variable aleatoria?
- ¿Cuáles son las hipótesis nulas y alternativas? Escribe las hipótesis nulas y alternativas en palabras y en símbolos.
- ¿Esta prueba es derecha, izquierda o de dos colas?
- ¿Cuál es el\(p\text{-value}\)?
- ¿Rechazas o no rechazas la hipótesis nula?
- En el nivel ___ de significancia, a partir de los datos de la muestra, hay ______ (es/no es) evidencia suficiente para concluir que ______.
- Calcular la d de Cohen e interpretarla.
Contestar
- dos medios
- desconocido
- Student's-t
- \(\bar{X}_{1} - \bar{X}_{2}\)
-
- \(H_{0}: \mu_{1} = \mu_{2}\)Hipótesis nula: las medias de los alfas ponderados son iguales.
- \(H_{a}: \mu_{1} \neq \mu_{2}\)Hipótesis alternativa: las medias de los alfas ponderados no son iguales.
- de dos colas
- \(p\text{-value} = 0.8787\)
- No rechace la hipótesis nula
- Esto indica que las tendencias en las acciones son aproximadamente las mismas en los 30 principales bancos de cada región.

Figura\(\PageIndex{4}\).
Nivel de significancia del 5%, a partir de los datos de la muestra, no hay evidencia suficiente para concluir que los alfas ponderados medios para los bancos en el noreste y el oeste son diferentes - \(d = 0.040\), Muy pequeño, porque 0.040 es menor que el valor de Cohen de 0.2 para tamaño de efecto pequeño. El tamaño de la diferencia de las medias de los alfas ponderados para las dos regiones de bancos es pequeño, lo que indica que no existe una diferencia significativa entre sus tendencias en las acciones.
Referencias
- Datos de Ingeniero Graduado + Carreras en Computación. Disponible en línea en www.graduatingengineer.com
- Datos de Microsoft Bookshelf.
- Datos del sitio web del Senado de los Estados Unidos, disponible en línea en www.Senate.gov (consultado el 17 de junio de 2013).
- “Lista de los actuales Senadores de Estados Unidos por Edad”. Wikipedia. Disponible en línea en es.wikipedia.org/wiki/list_of... enators_by_age (consultado el 17 de junio de 2013).
- “Sectorización por Grupos Industriales”. Nasdaq. Disponible en línea en www.nasdaq.com/markets/barcha... &base=industry (consultado el 17 de junio de 2013).
- “Clubes de striptease: donde suceden la prostitución y la trata”. Investigación y Educación sobre la Prostitución, 2013. Disponible en línea en www.ProstitutionResearch.com/ProsViolPostTraustress.html (consultado el 17 de junio de 2013).
- “Historia de la Serie Mundial”. Basebol-Almanaque, 2013. Disponible en línea en http://www.baseball-almanac.com/ws/wsmenu.shtml (consultado el 17 de junio de 2013).
Revisar
Dos medias poblacionales de muestras independientes donde no se conocen las desviaciones estándar de la población
- Variable aleatoria:\(\bar{X}_{1} - \bar{X}_{2} =\) la diferencia de las medias de muestreo
- Distribución: T -distribución del estudiante con grados de libertad (varianzas no agrupadas)
Revisión de Fórmula
Error estándar:\[SE = \sqrt{\dfrac{(s_{1}^{2})}{n_{1}} + \dfrac{(s_{2}^{2})}{n_{2}}}\]
Estadística de prueba (t -score):\[t = \dfrac{(\bar{x}_{1}-\bar{x}_{2}) - (\mu_{1}-\mu_{2})}{\sqrt{\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}}}\]
Grados de libertad:
\[df = \dfrac{\left(\dfrac{(s_{1})^{2}}{n_{1}} + \dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}}{\left(\dfrac{1}{n_{1} - 1}\right)\left(\dfrac{(s_{1})^{2}}{n_{1}}\right)^{2}} + \left(\dfrac{1}{n_{2} - 1}\right)\left(\dfrac{(s_{2})^{2}}{n_{2}}\right)^{2}\]
donde:
- \(s_{1}\)y\(s_{2}\) son las desviaciones estándar de la muestra, y n 1 y n 2 son los tamaños de muestra.
- \(x_{1}\)y\(x_{2}\) son las medias de la muestra.
Cohen\(d\) es la medida del tamaño del efecto:
\[d = \dfrac{\bar{x}_{1} - \bar{x}_{2}}{s_{\text{pooled}}}\]
donde
\[s_{\text{pooled}} = \sqrt{\dfrac{(n_{1} - 1)s^{2}_{1} + (n_{2} - 1)s^{2}_{2}}{n_{1} + n_{2} - 2}}\]
Glosario
- Grados de Libertad (\(df\))
- el número de objetos en una muestra que son libres de variar.
- Desviación estándar
- Un número que es igual a la raíz cuadrada de la varianza y mide qué tan lejos están los valores de los datos de su media; notación:\(s\) para la desviación estándar de la muestra y\(\sigma\) para la desviación estándar de la población.
- Variable (Variable aleatoria)
- una característica de interés en una población en estudio. La notación común para las variables son letras latinas mayúsculas\(X, Y, Z,\)... Notación común para un valor específico del dominio (conjunto de todos los valores posibles de una variable) son letras latinas minúsculas\(x, y, z,\)... Por ejemplo, si\(X\) es el número de hijos en una familia, entonces\(x\) representa un entero específico 0, 1, 2, 3,... Las variables en estadística difieren de las variables en álgebra intermedia en las dos formas siguientes.
- El dominio de la variable aleatoria (RV) no es necesariamente un conjunto numérico; el dominio puede expresarse en palabras; por ejemplo, si el color\(X =\) del cabello, entonces el dominio es {negro, rubio, gris, verde, naranja}.
- Podemos decir qué valor específico x de la variable aleatoria\(X\) toma solo después de realizar el experimento.


