13.5: Prueba de dos varianzas
- Page ID
- 153480
Otro de los usos de la\(F\) distribución es probar dos varianzas. A menudo es deseable comparar dos varianzas en lugar de dos promedios. Por ejemplo, a los administradores universitarios les gustaría que dos profesores universitarios que califiquen los exámenes tengan la misma variación en su calificación. Para que una tapa se ajuste a un recipiente, la variación en la tapa y el recipiente debe ser la misma. Un supermercado podría estar interesado en la variabilidad de los horarios de salida para dos damas.
para realizar un\(F\) test of two variances, it is important that the following are true:
- Las poblaciones de las que se extraen las dos muestras se distribuyen normalmente.
- Las dos poblaciones son independientes entre sí.
A diferencia de la mayoría de las otras pruebas de este libro, la\(F\) prueba para la igualdad de dos varianzas es muy sensible a las desviaciones de la normalidad. Si las dos distribuciones no son normales, la prueba puede dar\(p\text{-values}\) mayores de lo que debería, o inferiores, de formas impredecibles. Muchos textos sugieren que los estudiantes no utilizan esta prueba en absoluto, pero en aras de la integridad la incluimos aquí.
Supongamos que se toma una muestra aleatoria de dos poblaciones normales independientes. Dejar\(\sigma^{2}_{1}\) y\(\sigma^{2}_{2}\) ser las varianzas poblacionales y\(s^{2}_{1}\) y\(s^{2}_{2}\) ser las varianzas de la muestra. Deje que los tamaños de muestra sean\(n_{1}\) y\(n_{2}\). Dado que estamos interesados en comparar las dos varianzas de muestra, utilizamos la\(F\) relación:
\[F = \dfrac{\left[\dfrac{(s_{1})^{2}}{(\sigma_{1})^{2}}\right]}{\left[\dfrac{(s_{2})^{2}}{(\sigma_{2})^{2}}\right]}\]
\(F\)tiene la distribución
\[F \sim F(n_{1} - 1, n_{2} - 1)\]
donde\(n_{1} - 1\) están los grados de libertad para el numerador y\(n_{2} - 1\) son los grados de libertad para el denominador.
Si la hipótesis nula es\(\sigma^{2}_{1} = \sigma^{2}_{2}\), entonces el\(F\) Ratio se convierte en
\[F = \dfrac{\left[\dfrac{(s_{1})^{2}}{(\sigma_{1})^{2}}\right]}{\left[\dfrac{(s_{2})^{2}}{(\sigma_{2})^{2}}\right]} = \dfrac{(s_{1})^{2}}{(s_{2})^{2}}.\]
La\(F\) relación también podría ser\(\dfrac{(s_{2})^{2}}{(s_{1})^{2}}\). Depende de\(H_{a}\) y de qué varianza muestral es mayor.
Si las dos poblaciones tienen varianzas iguales, entonces\(s^{2}_{1}\) y\(s^{2}_{2}\) están cerca en valor y\(F = \dfrac{(s_{1})^{2}}{(s_{2})^{2}}\) está cerca de una. Pero si las dos varianzas poblacionales son muy diferentes,\(s^{2}_{1}\) y\(s^{2}_{2}\) tienden a ser muy diferentes, también. Elegir\(s^{2}_{1}\) como la varianza de la muestra más grande hace que la relación sea mayor\(\dfrac{(s_{1})^{2}}{(s_{2})^{2}}\) a uno. Si\(s^{2}_{1}\) y\(s^{2}_{2}\) están muy separados, entonces
\[F = \dfrac{(s_{1})^{2}}{(s_{2})^{2}}\]
es un gran número.
Por lo tanto, si\(F\) es cercano a uno, la evidencia favorece la hipótesis nula (las dos varianzas poblacionales son iguales). Pero si\(F\) es mucho mayor que uno, entonces la evidencia está en contra de la hipótesis nula. Una prueba de dos varianzas puede ser izquierda, derecha o de dos colas.
Una prueba de dos varianzas puede ser izquierda, derecha o de dos colas.
Ejemplo\(\PageIndex{1}\)
Dos instructores universitarios están interesados en saber si hay o no alguna variación en la forma en que califica los exámenes de matemáticas. Cada uno califica el mismo conjunto de 30 exámenes. Las calificaciones del primer instructor tienen una varianza de 52.3. Las calificaciones del segundo instructor tienen una varianza de 89.9. Pruebe la afirmación de que la varianza del primer instructor es menor. (En la mayoría de las universidades, es deseable que las variaciones de las calificaciones de los exámenes sean casi las mismas entre los instructores). El nivel de significancia es del 10%.
Contestar
Sea 1 y 2 los subíndices que indiquen el primer y segundo instructor, respectivamente.
- \(n_{1} = n_{2} = 30\).
- \(H_{0}: \sigma^{2}_{1} = \sigma^{2}_{2}\)y\(H_{a}: \sigma^{2}_{1} < \sigma^{2}_{2}\)
Calcular el estadístico de prueba: Por la hipótesis nula\(\sigma^{2}_{1} = \sigma^{2}_{2})\), el\(F\) estadístico es:
\[F = \dfrac{\left[\dfrac{(s_{1})^{2}}{(\sigma_{1})^{2}}\right]}{\left[\dfrac{(s_{2})^{2}}{(s_{2})^{2}}\right]} = \dfrac{(s_{1})^{2}}{(s_{2})^{2}} = \dfrac{52.3}{89.9} = 0.5818\]
Distribución para la prueba:\(F_{29,29}\) dónde\(n_{1} - 1 = 29\) y\(n_{2} - 1 = 29\).
Gráfica: Esta prueba es de cola izquierda.
Dibuja la gráfica etiquetando y sombreando apropiadamente.
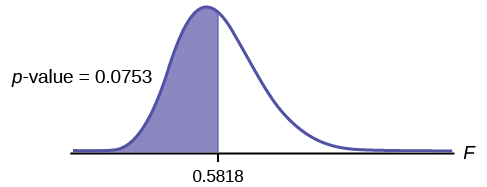
Declaración de probabilidad:\(p\text{-value} = P(F < 0.5818) = 0.0753\)
Comparar\(\alpha\) y el\(p\text{-value}\):\(\alpha = 0.10 \alpha > p\text{-value}\).
Tomar una decisión: Desde\(\alpha > p\text{-value}\), rechazar\(H_{0}\).
Conclusión: Con un nivel de significancia del 10%, a partir de los datos, hay evidencia suficiente para concluir que la varianza en las calificaciones para el primer instructor es menor.
Presiona STAT y flecha hacia TEST. Flecha hacia abajo a D:2-SampfTest. Presione ENTER. Flecha hacia Estadísticas y presiona ENTRAR. Para Sx1, n1, Sx2 y n2, ingrese (52.3) −−−−√ (52.3), 30, (89.9) −−−−−√ (89.9) y 30. Presione ENTRAR después de cada uno. Flecha a σ1: y <σ2. Presione ENTER. Flecha hacia abajo para Calcular y presiona ENTRAR. F = 0.5818 y p -valor = 0.0753. Vuelva a realizar el procedimiento e intente Dibujar en lugar de Calcular.
Ejercicio\(\PageIndex{1}\)
La Sociedad Coral de Nueva York divide a los cantantes masculinos en cuatro categorías, desde las voces más altas hasta las más bajas: Tenor1, Tenor2, Bass1, Bass2. En la tabla están las alturas de los hombres en los grupos Tenor1 y Bass2. Se sospecha que los hombres más altos tendrán voces más bajas, y que la varianza de altura también puede subir con las voces más bajas. ¿Tenemos buena evidencia de que la varianza de las alturas de los cantantes en cada uno de estos dos grupos (Tenor1 y Bass2) son diferentes?
| Tenor1 | Bass2 | Tenor 1 | Bajo 2 | Tenor 1 | Bajo 2 |
|---|---|---|---|---|---|
| 69 | 72 | 67 | 72 | 68 | 67 |
| 72 | 75 | 70 | 74 | 67 | 70 |
| 71 | 67 | 65 | 70 | 64 | 70 |
| 66 | 75 | 72 | 66 | 69 | |
| 76 | 74 | 70 | 68 | 72 | |
| 74 | 72 | 68 | 75 | 71 | |
| 71 | 72 | 64 | 68 | 74 | |
| 66 | 74 | 73 | 70 | 75 | |
| 68 | 72 | 66 | 72 |
Contestar
Los histogramas no son tan normales como a uno le gustaría. Trazarlos para verificar. No obstante, procedemos con la prueba en cualquier caso.
Subíndices:\(\text{T1} =\) tenor 1 y\(\text{B2} =\) bajo 2
Las desviaciones estándar de las muestras son\(s_{\text{T1}} = 3.3302\) y\(s_{\text{B2}} = 2.7208\).
Las hipótesis son
\(H_{0}: \sigma^{2}_{\text{T1}} = \sigma^{2}_{\text{B2}}\)y\(H_{0}: \sigma^{2}_{\text{T1}} \neq \sigma^{2}_{\text{B2}}\) (prueba de dos colas)
El\(F\) estadístico es\(1.4894\) con 20 y 25 grados de libertad.
El\(p\text{-value}\) es\(0.3430\). Si asumimos que alfa es 0.05, entonces no podemos rechazar la hipótesis nula.
No tenemos buena evidencia a partir de los datos de que las alturas de los cantantes de Tenor1 y Bass2 tienen diferentes varianzas (a pesar de haber una diferencia significativa en las alturas medias de aproximadamente 2.5 pulgadas).
Referencias
- “MLB Vs. Posiciones de División — 2012.” Disponible en línea en http://espn.go.com/mlb/standings/_/y...ion/order/true.
Revisar
La prueba F para la igualdad de dos varianzas descansa fuertemente en el supuesto de distribuciones normales. La prueba no es confiable si no se cumple esta suposición. Si ambas distribuciones son normales, entonces la relación de las dos varianzas muestrales se distribuye como un estadístico F, con grados de libertad del numerador y denominador que son uno menos que los tamaños de muestra de los dos grupos correspondientes. Una prueba de hipótesis de dos varianzas determina si dos varianzas son iguales. La distribución para la prueba de hipótesis es la\(F\) distribución con dos grados diferentes de libertad.
Supuestos:
- Las poblaciones de las que se extraen las dos muestras se distribuyen normalmente.
- Las dos poblaciones son independientes entre sí.
Revisión de Fórmula
\(F\)tiene la distribución\(F \sim F(n_{1} - 1, n_{2} - 1)\)
\(F = \dfrac{\dfrac{s^{2}_{1}}{\sigma^{2}_{1}}}{\dfrac{s^{2}_{2}}{\sigma^{2}_{2}}}\)
Si\(\sigma_{1} = \sigma_{2}\), entonces\(F = \dfrac{s^{2}_{1}}{s^{2}_{2}}\)


