2.3: Medidas de Variabilidad
- Page ID
- 151118
Objetivos de aprendizaje
- Conocer el concepto de variabilidad de un conjunto de datos.
- Aprender a calcular tres medidas de la variabilidad de un conjunto de datos: el rango, la varianza y la desviación estándar.
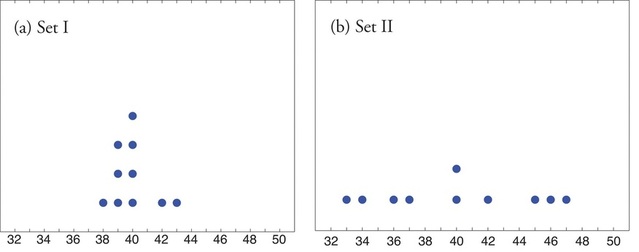
Observe los dos conjuntos de datos en Tabla\(\PageIndex{1}\) y la representación gráfica de cada uno, llamada gráfica de puntos, en la Figura\(\PageIndex{1}\).
| Conjunto de Datos I: | 40 | 38 | 42 | 40 | 39 | 39 | 43 | 40 | 39 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|
| Conjunto de Datos II: | 46 | 37 | 40 | 33 | 42 | 36 | 40 | 47 | 34 | 45 |
Los dos conjuntos de diez mediciones cada centro en el mismo valor: ambos tienen media, mediana y modo\(40\). Sin embargo, una mirada a la figura muestra que son marcadamente diferentes. En el Conjunto de Datos I las mediciones varían solo ligeramente desde el centro, mientras que para el Conjunto de Datos II las mediciones varían mucho. Así como hemos adjuntado números a un conjunto de datos para ubicar su centro, ahora deseamos asociar a cada conjunto de datos números que midan cuantitativamente cómo los datos se dispersan lejos del centro o clúster cercano a él. Estas nuevas cantidades se denominan medidas de variabilidad, y discutiremos tres de ellas.
La gama
Primero discutimos la medida más simple de variabilidad.
Definición: rango
El rango\(R\) de un conjunto de datos es la diferencia entre sus valores más grandes y más pequeños\[R=x_{\text{max}}−x_{\text{min}}\] donde\(\displaystyle x_{\text{max}}\) es la medida más grande en el conjunto de datos y\(\displaystyle x_{\text{min}}\) es la más pequeña.
Ejemplo\(\PageIndex{1}\): Identifyig the Range of a dataset
Encuentra el rango de cada conjunto de datos en Tabla\(\PageIndex{1}\).
Solución:
- Para el Conjunto de Datos I el máximo es\(43\) y el mínimo es\(38\), por lo que el rango es\(R=43−38=5\).
- Para el Conjunto de Datos II el máximo es\(47\) y el mínimo es\(33\), por lo que el rango es\(R=47−33=14\).
El rango es una medida de variabilidad porque indica el tamaño del intervalo sobre el cual se distribuyen los puntos de datos. Un rango menor indica menor variabilidad (menor dispersión) entre los datos, mientras que un rango mayor indica lo contrario.
La varianza y la desviación estándar
Las otras dos medidas de variabilidad que consideraremos son más elaboradas y también dependen de si el conjunto de datos es solo una muestra extraída de una población mucho mayor o es la población entera misma (es decir, un censo).
Definición: varianza muestral y desviación estándar muestral
La varianza de muestra de un conjunto de datos de\(n\) muestra es el número\(\mathbf{ s^2}\) definido por la fórmula
\[s^2 = \dfrac{\sum (x-\bar x)^2}{n-1}\]
que por álgebra es equivalente a la fórmula
\[s^2=\dfrac{\sum x^2 - \dfrac{1}{n}\left(\sum x\right)^2}{n-1}\]
La raíz cuadrada\(\mathbf s\) de la varianza de la muestra se denomina desviación estándar de la muestra de un conjunto de datos de\(n\) muestra. Está dado por las fórmulas
\[s = \sqrt{s^2} = \sqrt{\dfrac{\sum (x-\bar x)^2}{n-1} } = \sqrt{\dfrac{\sum x^2 - \dfrac{1}{n}\left(\sum x\right)^2}{n-1}}.\]
Si bien la primera fórmula en cada caso parece menos complicada que la segunda, esta última es más fácil de usar en cálculos manuales, y se llama fórmula de atajo.
Ejemplo\(\PageIndex{2}\): Identifying the Variance and Standard Deviation of a Dataset
Encuentra la varianza muestral y la desviación estándar muestral del Conjunto de Datos II en la Tabla\(\PageIndex{1}\).Solución
Para utilizar la fórmula definitoria (la primera fórmula) en la definición primero calculamos para cada observación\(x\) su desviación\(x-\bar x\) de la media muestral. Dado que la media de los datos es\(\bar x =40\), obtenemos los diez números mostrados en la segunda línea de la tabla suministrada
\[ \begin{array}{c|cccccccccc} x & 46 & 37 & 40 & 33 & 42 & 36 & 40 & 47 & 34 & 45 \\ \hline x−\bar{x} & -6 & -3 & 0 & -7 & 2 & -4 & 0 & 7 & -6 & 5 \end{array} \nonumber\]
Así
\[\sum (x-\bar{x})^2=6^2+(-3)^2+0^2+(-7)^2+2^2+(-4)^2+0^2+7^2+(-6)^2+5^2=224\nonumber\]
entonces la varianza es
\[s^2=\dfrac{\sum (x-\bar{x})^2}{n-1}=\dfrac{224}{9}=24.\bar{8} \nonumber\]
y la desviación estándar es
\[s=\sqrt{24.\bar{8}} \approx 4.99 \nonumber\]
Se anima al alumno a calcular las diez desviaciones para el Conjunto de Datos I y verificar que sus cuadrados suman\(20\), de manera que la varianza muestral y la desviación estándar del Conjunto de Datos I sean los números mucho más pequeños
\[s^2=20/9=2.\bar{2}\]
y
\[s=20/9 \approx 1.49\]
Ejemplo\(\PageIndex{2}\)
Encuentre la varianza muestral y la desviación estándar muestral de los diez GPA en “Ejemplo 2.2.3" en la Sección 2.2.
\[1.90\; \; 3.00\; \; 2.53\; \; 3.71\; \; 2.12\; \; 1.76\; \; 2.71\; \; 1.39\; \; 4.00\; \; 3.33\nonumber\]
Solución
Desde
\[ \sum x = 1.90 + 3.00+ 2.53 + 3.71 + 2.12 + 1.76 + 2.71 + 1.39 + 4.00 + 3.33 = 26.45 \nonumber\]
y
\[ \sum x^2 = 1.902 + 3.002 + 2.532 + 3.712 + 2.122+ 1.762 + 2.712 + 1.392 + 4.002 + 3.332 = 76.7321 \nonumber\]
la fórmula de acceso directo da
\[ s^2=\dfrac{\sum x^2−(\sum x)^2}{n−1}=\dfrac{76.7321−(26.45)^2/10}{10−1}=\dfrac{6.77185}{9}=0.75242\bar{7} \nonumber \]
y
\[ s=\sqrt{0.75242\bar{7}}\approx 0.867 \nonumber\]
La varianza muestral tiene diferentes unidades a partir de los datos. Por ejemplo, si las unidades en el conjunto de datos fueran pulgadas, las nuevas unidades serían pulgadas cuadradas o pulgadas cuadradas. Por lo tanto, es primordialmente de importancia teórica y no se considerará más a fondo en este texto, salvo de pasada.
Si el conjunto de datos comprende toda la población, entonces la desviación estándar poblacional, denotada\(\sigma\) (la letra griega minúscula sigma), y su cuadrado, la varianza poblacional\(\sigma ^2\), se definen de la siguiente manera.
Definiciones: La varianza poblacional\(\mathbf{\sigma^2}\) and population standard deviation \(\mathbf \sigma\)
La variabilidad de un conjunto de datos\(N\) poblacionales se mide por la varianza poblacional
\[\sigma^2=\dfrac{\sum (x−\mu)^2}{N} \label{popVar}\]
y su raíz cuadrada, la desviación estándar de la población
\[\sigma =\sqrt{\dfrac{\sum (x−\mu)^2}{N}}\label{popSTD}\]
donde\(\mu\) está la media poblacional como se definió anteriormente.
Obsérvese que el denominador en la fracción es el número completo de observaciones, no ese número reducido en una, como es el caso de la desviación estándar de la muestra. Dado que la mayoría de los conjuntos de datos son muestras, siempre trabajaremos con la desviación estándar y varianza de la muestra.
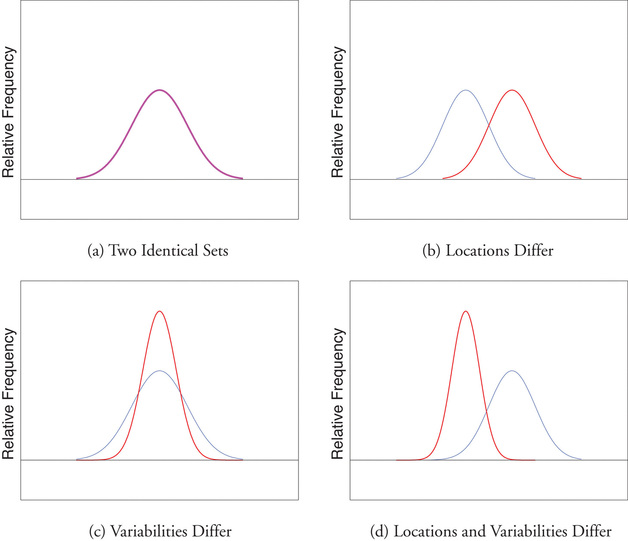
Finalmente, en muchas situaciones de la vida real los problemas estadísticos más importantes tienen que ver con comparar las medias y desviaciones estándar de dos conjuntos de datos. La figura\(\PageIndex{2}\) ilustra cómo una diferencia en una o ambas de la media de la muestra y la desviación estándar de la muestra se reflejan en la apariencia del conjunto de datos como lo muestran las curvas derivadas de los histogramas de frecuencia relativa construidos usando los datos.
Llave para llevar
El rango, la desviación estándar y la varianza dan cada uno una respuesta cuantitativa a la pregunta “¿Qué variables son los datos?”

