2.4: Posición relativa de los datos

Última actualización
Guardar como PDF

Page ID: 151108

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Aprender el concepto de la posición relativa de un elemento de un conjunto de datos.
Conocer el significado de cada una de las dos medidas, el rango percentil y la\(z\) -score, de la posición relativa de una medida y cómo computar cada una.
Aprender el significado de los tres cuartiles asociados a un conjunto de datos y cómo calcularlos.
Aprender el significado del resumen de cinco números de un conjunto de datos, cómo construir la gráfica de caja asociada a él y cómo interpretar la gráfica de caja.

Cuando tomas un examen, lo que a menudo es tan importante como tu puntaje real en el examen es la forma en que tu puntaje se compara con el desempeño de otros estudiantes. Si hiciste un\(70\) pero la puntuación promedio (ya sea la media, mediana o modo) fue\(85\), lo hiciste relativamente mal. Si hiciste un\(70\) pero el puntaje promedio fue solo\(55\) entonces lo hiciste relativamente bien. En general, la significación de un valor observado en un conjunto de datos depende en gran medida de cómo ese valor se compara con los otros valores observados en un conjunto de datos. Por lo tanto, deseamos adjuntar a cada valor observado un número que mida su posición relativa.

Percentiles y cuartiles

Cualquiera que haya realizado una prueba nacional estandarizada está familiarizado con la idea de que se le otorgue tanto una puntuación en el examen como un “ranking percentil” de esa puntuación. Te pueden decir que tu puntaje fue\(625\) y que es el\(85^{th}\) percentil. El primer número cuenta cómo te fue realmente en el examen; el segundo dice que\(85\%\) de las puntuaciones en el examen fueron menores o iguales a tu puntuación,\(625\).

Definición: percentil de datos

Dado un valor observado\(x\) en un conjunto de datos,\(x\) es el\(P^{th}\) percentil de los datos si\(P\%\) de los datos son menores o iguales a\(x\). El número\(P\) es el rango percentil de\(x\).

Ejemplo\(\PageIndex{1}\)

¿Qué percentil es el valor\(1.39\) en el conjunto de datos de diez GPA considerados en un Ejemplo anterior? ¿Qué percentil es el valor\(3.33\)?

Solución:

Los datos, escritos en orden creciente, son

\[ \begin{array}{cccccccccc} 1.39 & 1.76 & 1.90 & 2.12 & 2.53 & 2.71 & 3.00 & 3.33 & 3.71 & 4.00 \end{array}\]

El único valor de datos que es menor o igual a\(1.39\) es\(1.39\) en sí mismo. Dado\(1\) que de cada diez, o\(1/10=10\%\), de los puntos de datos son menores o iguales a\(1.39\),\(1.39\) es el\(10^{th}\) percentil. Ocho valores de datos son menores o iguales a\(3.33\). Dado\(8\) que de cada diez, o\(8∕10 = .80 = 80\%\) de los valores de datos son menores o iguales a\(3.33\), el valor\(3.33\) es el\(80^{th}\) percentil de los datos.

El percentil P ^th corta el conjunto de datos en dos de manera que aproximadamente\(P\%\) de los datos se encuentran debajo de él y\((100−P)\% \) de los datos se encuentran por encima de él. En particular, los tres percentiles que cortan los datos en cuartos, como se muestra en la Figura\(\PageIndex{1}\), se denominan los cuartiles de un conjunto de datos. Los cuartiles son los tres números\(Q_1\),\(Q_2\),\(Q_3\) que dividen el conjunto de datos aproximadamente en cuartos. La siguiente definición computacional simple de los tres cuartiles funciona bien en la práctica.

Figura\(\PageIndex{1}\): División de Datos por Cuartiles

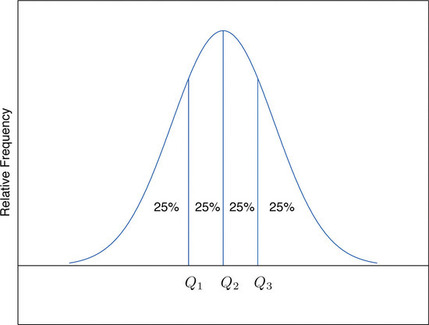
Definición: cuartil

Para cualquier conjunto de datos:

El segundo cuartil\(Q_2\) del conjunto de datos es su mediana.
Defina dos subconjuntos:
1. el conjunto inferior: todas las observaciones que son estrictamente menores que\(Q_2\)
2. el conjunto superior: todas las observaciones que son estrictamente mayores que\(Q_2\)
El primer cuartil\(Q_1\) del conjunto de datos es la mediana del conjunto inferior.
El tercer cuartil\(Q_3\) del conjunto de datos es la mediana del conjunto superior.

Ejemplo\(\PageIndex{2}\)

Encuentra los cuartiles del conjunto de datos de GPA de comentado en un Ejemplo anterior.

Solución:

Al igual que en el ejemplo anterior, primero enumeramos los datos en orden numérico:

\[\begin{array}{cccccccccc} 1.39 & 1.76 & 1.90 & 2.12 & 2.53 & 2.71 & 3.00 & 3.33 & 3.71 & 4.00 \end{array} \nonumber\]

Este conjunto de datos tiene\(n=10\) observaciones. Dado que\(10\) es un número par, la mediana es la media de las dos observaciones medias:

\[\tilde x=(2.53+2.71)∕2=2.62. \nonumber\]

Así lo es el segundo cuartil\(Q_2=2.62\). Los subconjuntos inferior y superior son

Inferior:\(L=\{1.39,1.76,1.90,2.12,2.53\}\),
Superior:\(U=\{2.71,3.00,3.33,3.71,4.00\}\).

Cada uno tiene un número impar de elementos, por lo que la mediana de cada uno es su observación media. Así, el primer cuartil es\(Q_1=1.90\), la mediana de\(L\), y el tercer cuartil es\(Q_3=3.33\), la mediana de\(U\).

Ejemplo\(\PageIndex{3}\)

Colinguen la observación\(3.88\) al conjunto de datos del ejemplo anterior y encuentren los cuartiles del nuevo conjunto de datos.

Solución:

Al igual que en el ejemplo anterior, primero enumeramos los datos en orden numérico:

\[\begin{array}{ccccccccccc} 1.39 & 1.76 & 1.90 & 2.12 & 2.53 & 2.71 & 3.00 & 3.33 & 3.71 & 3.88, 4.00 \end{array} \nonumber\]

Este conjunto de datos tiene\(11\) observaciones. El segundo cuartil es su mediana, el valor medio\(2.71\). Así\(Q_2=2.71\). Los subconjuntos inferior y superior son ahora

Inferior:\(L=\{1.39,1.76,1.90,2.12,2.53\}\)
Superior:\(U=\{3.00,3.33,3.71,3.88,4.00\}\).

El conjunto inferior\(L\) tiene la mediana, el valor medio,\(1.90\), entonces\(Q_1=1.90\). El conjunto superior tiene mediana\(3.71\), entonces\(Q_3=3.71\).

Además de los tres cuartiles, los dos valores extremos, el mínimo\(x_{min}\) y el máximo también\(x_{max}\) son útiles para describir todo el conjunto de datos. Juntos estos cinco números se denominan el resumen de cinco números de un conjunto de datos,

{\(X_{min}\),\(Q_1\),\(Q_2\),\(Q_3\),\(X_{max}\)}

El resumen de cinco números se utiliza para construir una gráfica de caja, como en la Figura\(\PageIndex{2}\). Cada uno de los cinco números está representado por un segmento de línea vertical, se forma una caja usando los segmentos de línea en\(Q_1\) y\(Q_3\) como sus dos lados verticales, y dos segmentos de línea horizontales se extienden desde los segmentos verticales que marcan\(Q_1\) y\(Q_3\) hasta los valores extremos adyacentes. (Los dos segmentos de línea horizontal se conocen como “bigotes”, y el diagrama a veces se llama “diagrama de caja y bigotes”). Advertimos al lector que existen otros tipos de parcelas de caja que difieren algo de las que estamos construyendo, aunque todas se basan en los tres cuartiles.

Figura\(\PageIndex{2}\): La Gráfica de Caja

Tenga en cuenta que la distancia de\(Q1\) a\(Q3\) es la longitud del intervalo sobre el cual la mitad media del rango de datos. Así tiene el siguiente nombre especial.

Definición: rango intercuartílico

El rango intercuartílico\(IQR\) es la cantidad

\[IQR = Q3-Q1\]

Ejemplo\(\PageIndex{4}\)

Construye un diagrama de caja y encuentra el\(IQR\) para los datos en Ejemplo\(\PageIndex{3}\).

Solución:

De nuestro trabajo en Ejemplo\(\PageIndex{1}\), sabemos que el resumen de cinco números es

\(X_{min} = 1.39\)
\(Q1 = 1.90\)
\(Q2 = 2.62\)
\(Q3 = 3.33\)
\(X_{max} = 4.00\)

El diagrama de caja es:

alt

El rango intercuartílico es:\(IQR=3.33-1.90=1.43\).

\(z\)-Puntuaciones

Otra forma de ubicar una observación particular\(x\) en un conjunto de datos es computar su distancia desde la media en unidades de desviación estándar. El\(z\) -score indica cuántas desviaciones estándar\(x\) es una observación individual desde el centro del conjunto de datos, su media. Se utiliza en distribuciones que han sido estandarizadas, lo que nos permite comprender mejor sus propiedades. Si\(z\) es negativo entonces\(x\) está por debajo de la media. Si\(z\) es\(0\) entonces\(x\) es igual a la media. Si\(z\) es positivo entonces\(x\) está por encima de la media

Definición:\(z\) -score

El\(z\) -score de una observación\(x\) es el número\(z\) dado por la fórmula computacional

\[z = \dfrac{x - \mu}{\sigma}\]

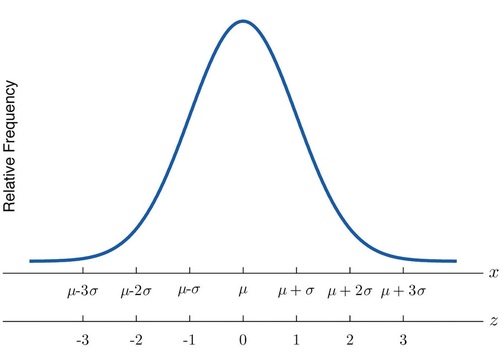
Figura\(\PageIndex{3}\): x -Escala versus z -Score

Ejemplo\(\PageIndex{5}\)

Supongamos que la media y desviación estándar de los GPA's de todos los estudiantes actualmente registrados en una universidad son\(\mu = 2.70\) y\(\sigma = 0.50\). Los\(z\) -puntajes de los GPA's de dos estudiantes, Antonio y Beatrice, son\(z=-0.62\) y\(z=1.28\), respectivamente. ¿Cuáles son sus GPA?

Solución:

Usando la segunda fórmula justo después de la definición de\(z\) -scores, calculamos los GPA como

Antonio:\(x=\mu +z\sigma =2.70+(-0.62)(0.50)=2.39\)
Beatriz:\(x=\mu +z\sigma =2.70+(1.28)(0.50)=3.34\)

Principales conclusiones

El rango percentil y\(z\) -score de una medida indican su posición relativa con respecto a las otras mediciones en un conjunto de datos.
Los tres cuartiles dividen un conjunto de datos en cuartos.
El resumen de cinco números y su diagrama de caja asociado resumen la ubicación y distribución de los datos.