4.2: Distribuciones de probabilidad para variables aleatorias discretas
- Page ID
- 151199
Objetivos de aprendizaje
- Aprender el concepto de distribución de probabilidad de una variable aleatoria discreta.
- Aprender los conceptos de media, varianza y desviación estándar de una variable aleatoria discreta, y cómo calcularlos.
Asociada a cada valor posible\(x\) de una variable aleatoria discreta\(X\) está la probabilidad de\(P(x)\) que\(X\) tome el valor\(x\) en un ensayo del experimento.
Definición: distribución de probabilidad
La distribución de probabilidad de una variable aleatoria discreta\(X\) es una lista de cada valor posible de\(X\) junto con la probabilidad que\(X\) toma ese valor en un ensayo del experimento.
Las probabilidades en la distribución de probabilidad de una variable aleatoria\(X\) deben cumplir las dos condiciones siguientes:
- Cada probabilidad\(P(x)\) debe estar entre\(0\) y\(1\):\[0\leq P(x)\leq 1.\]
- La suma de todas las probabilidades posibles es\(1\):\[\sum P(x)=1.\]
Ejemplo\(\PageIndex{1}\): two Fair Coins
Una moneda justa se arroja dos veces. \(X\)Sea el número de cabezas que se observen.
- Construir la distribución de probabilidad de\(X\).
- Encuentra la probabilidad de que se observe al menos una cabeza.
Solución:
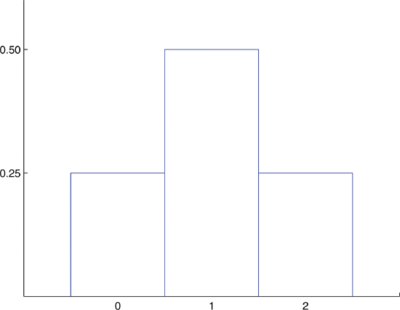
- Los valores posibles que\(X\) pueden tomar son\(0\),\(1\), y\(2\). Cada uno de estos números corresponde a un evento en el espacio muestral\(S=\{hh,ht,th,tt\}\) de resultados igualmente probables para este experimento:\[X = 0\; \text{to}\; \{tt\},\; X = 1\; \text{to}\; \{ht,th\}, \; \text{and}\; X = 2\; \text{to}\; {hh}. \nonumber\] La probabilidad de cada uno de estos eventos, de ahí del valor correspondiente de\(X\), se puede encontrar simplemente contando, para dar\[\begin{array}{c|ccc} x & 0 & 1 & 2 \\ \hline P(x) & 0.25 & 0.50 & 0.25\\ \end{array} \nonumber\] Esta tabla es la probabilidad distribución de\(X\).
- “Al menos una cabeza” es el evento\(X\geq 1\), que es la unión de los eventos mutuamente excluyentes\(X = 1\) y\(X = 2\). Así, en la Figura se da\[ \begin{align*} P(X\geq 1)&=P(1)+P(2)=0.50+0.25 \\[5pt] &=0.75 \end{align*}\] un histograma que ilustra gráficamente la distribución de probabilidad\(\PageIndex{1}\).
Ejemplo\(\PageIndex{2}\): Two Fair Dice
Se tira un par de dados justos. Dejar\(X\) denotar la suma del número de puntos en las caras superiores.
- Construir la distribución de probabilidad de\(X\) para un dado pagado de justo.
- Encuentra\(P(X\geq 9)\).
- Encuentra la probabilidad de que\(X\) tome un valor par.
Solución:
El espacio muestral de resultados igualmente probables es
\[\begin{matrix} 11 & 12 & 13 & 14 & 15 & 16\\ 21 & 22 & 23 & 24 & 25 & 26\\ 31 & 32 & 33 & 34 & 35 & 36\\ 41 & 42 & 43 & 44 & 45 & 46\\ 51 & 52 & 53 & 54 & 55 & 56\\ 61 & 62 & 63 & 64 & 65 & 66 \end{matrix} \nonumber\]
donde el primer dígito es die 1 y el segundo número es die 2.
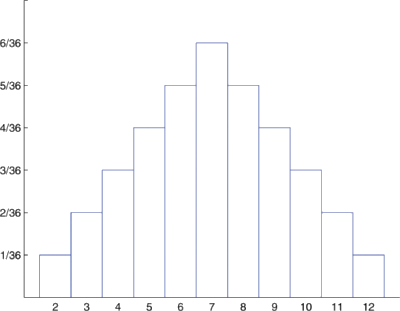
- Los valores posibles para\(X\) son los números\(2\) a través de\(12\). \(X= 2\)es el evento\(\{11\}\), entonces\(P(2)=1/36\). \(X= 3\)es el evento\(\{12,21\}\), entonces\(P(3)=2/36\). Continuando de esta manera obtenemos la siguiente tabla\[\begin{array}{c|ccccccccccc} x &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12 \\ \hline P(x) &\dfrac{1}{36} &\dfrac{2}{36} &\dfrac{3}{36} &\dfrac{4}{36} &\dfrac{5}{36} &\dfrac{6}{36} &\dfrac{5}{36} &\dfrac{4}{36} &\dfrac{3}{36} &\dfrac{2}{36} &\dfrac{1}{36} \\ \end{array} \nonumber\] Esta tabla es la distribución de probabilidad de\(X\).
- El evento\(X\geq 9\) es la unión de los eventos mutuamente excluyentes\(X = 9\),\(X = 10\),\(X = 11\), y\(X = 12\). Así\[\begin{align*}P(X\geq 9) &=P(9)+P(10)+P(11)+P(12) \\[5pt] &=\dfrac{4}{36}+\dfrac{3}{36}+\dfrac{2}{36}+\dfrac{1}{36} \\[5pt] &=\dfrac{10}{36} \\[5pt] &=0.2\bar{7} \end{align*}\]
- Antes saltamos inmediatamente a la conclusión de que la probabilidad que\(X\) toma un valor par debe ser\(0.5\), tenga en cuenta que\(X\) toma seis valores pares diferentes pero sólo cinco valores impares diferentes. Calculamos\[\begin{align*} P(X\; \text{is even}) &= P(2)+P(4)+P(6)+P(8)+P(10)+P(12) \\[5pt] &= \dfrac{1}{36}+\dfrac{3}{36}+\dfrac{5}{36}+\dfrac{5}{36}+\dfrac{3}{36}+\dfrac{1}{36} \\[5pt] &= \dfrac{18}{36} \\[5pt] &= 0.5 \end{align*}\] Un histograma que ilustra gráficamente la distribución de probabilidad se da en la Figura\(\PageIndex{2}\).
La media y la desviación estándar de una variable aleatoria discreta
Definición: mean
La media (también llamada “valor de expectativa” o “valor esperado”) de una variable aleatoria discreta\(X\) es el número
\[\mu =E(X)=\sum x P(x) \label{mean}\]
La media de una variable aleatoria puede interpretarse como la media de los valores asumidos por la variable aleatoria en ensayos repetidos del experimento.
Ejemplo\(\PageIndex{3}\)
Encuentra la media de la variable aleatoria discreta\(X\) cuya distribución de probabilidad es
\[\begin{array}{c|cccc} x &-2 &1 &2 &3.5\\ \hline P(x) &0.21 &0.34 &0.24 &0.21\\ \end{array} \nonumber\]
Solución
Usando la definición de media (Ecuación\ ref {media}) da
\[\begin{align*} \mu &= \sum x P(x)\\[5pt] &= (-2)(0.21)+(1)(0.34)+(2)(0.24)+(3.5)(0.21)\\[5pt] &= 1.135 \end{align*}\]
Ejemplo\(\PageIndex{4}\)
Una organización de servicios en un pueblo grande organiza una rifa cada mes. Se venden mil boletos de rifa por\(\$1\) cada uno. Cada uno tiene las mismas posibilidades de ganar. El primer premio es\(\$300\), el segundo premio es\(\$200\), y el tercer premio es\(\$100\). Dejar\(X\) denotar la ganancia neta de la compra de un boleto.
- Construir la distribución de probabilidad de\(X\).
- Encuentra la probabilidad de ganar dinero en la compra de un boleto.
- Encontrar el valor esperado de\(X\), e interpretar su significado.
Solución:
- Si se selecciona un boleto como ganador del primer premio, la ganancia neta para el comprador es el\(\$300\) premio menos el\(\$1\) que se pagó por el boleto, de ahí\(X = 300-11 = 299\). Hay uno de esos boletos, entonces\(P(299) = 0.001\). Al aplicar el mismo principio de “ingresos menos salida” a los ganadores del segundo y tercer premio y a los boletos\(997\) perdedores se obtiene la distribución de probabilidad:\[\begin{array}{c|cccc} x &299 &199 &99 &-1\\ \hline P(x) &0.001 &0.001 &0.001 &0.997\\ \end{array} \nonumber\]
- Dejar\(W\) denotar el evento de que se selecciona un boleto para ganar uno de los premios. Uso de la tabla\[\begin{align*} P(W)&=P(299)+P(199)+P(99)=0.001+0.001+0.001\\[5pt] &=0.003 \end{align*}\]
- Usando la definición de valor esperado (Ecuación\ ref {media}),\[\begin{align*}E(X)&=(299)\cdot (0.001)+(199)\cdot (0.001)+(99)\cdot (0.001)+(-1)\cdot (0.997) \\[5pt] &=-0.4 \end{align*}\] El valor negativo significa que uno pierde dinero en promedio. En particular, si alguien comprara boletos repetidamente, entonces aunque ganaría de vez en cuando, en promedio perdería\(40\) centavos por boleto comprado.
El concepto de valor esperado también es básico para la industria aseguradora, como lo ilustra el siguiente ejemplo simplificado.
Ejemplo\(\PageIndex{5}\)
Una compañía de seguros de vida venderá una póliza de seguro de vida a término de un\(\$200,000\) año a una persona en un grupo de riesgo en particular por una prima de\(\$195\). Encuentre el valor esperado para la empresa de una sola póliza si una persona de este grupo de riesgo tiene\(99.97\%\) posibilidades de sobrevivir un año.
Solución:
Dejar\(X\) denotar la ganancia neta a la empresa por la venta de una de esas pólizas. Hay dos posibilidades: el asegurado vive todo el año o el asegurado muere antes de que termine el año. Aplicando el principio de “ingreso menos salida”, en el primer caso el valor de\(X\) es\(195-0\); en el segundo caso lo es\(195-200,000=-199,805\). Dado que la probabilidad en el primer caso es 0.9997 y en el segundo caso es\(1-0.9997=0.0003\), la distribución de probabilidad para\(X\) es:
\[\begin{array}{c|cc} x &195 &-199,805 \\ \hline P(x) &0.9997 &0.0003 \\ \end{array}\nonumber \]
Por lo tanto
\[\begin{align*} E(X) &=\sum x P(x) \\[5pt]&=(195)\cdot (0.9997)+(-199,805)\cdot (0.0003) \\[5pt] &=135 \end{align*}\]
Ocasionalmente (de hecho,\(3\) veces en\(10,000\)) la compañía pierde una gran cantidad de dinero en una póliza, pero normalmente gana\(\$195\), lo que por nuestro cálculo de\(E(X)\) funciona a una ganancia neta de\(\$135\) por póliza vendida, en promedio.
Definición: varianza
La varianza (\(\sigma ^2\)) de una variable aleatoria discreta\(X\) es el número
\[\sigma ^2=\sum (x-\mu )^2P(x) \label{var1}\]
que por álgebra es equivalente a la fórmula
\[\sigma ^2=\left [ \sum x^2 P(x)\right ]-\mu ^2 \label{var2}\]
Definición: desviación estándar
La desviación estándar,\(\sigma \), de una variable aleatoria discreta\(X\) es la raíz cuadrada de su varianza, de ahí viene dada por las fórmulas
\[\sigma =\sqrt{\sum (x-\mu )^2P(x)}=\sqrt{\left [ \sum x^2 P(x)\right ]-\mu ^2} \label{std}\]
La varianza y desviación estándar de una variable aleatoria discreta\(X\) puede interpretarse como medidas de la variabilidad de los valores asumidos por la variable aleatoria en ensayos repetidos del experimento. Las unidades en la desviación estándar coinciden con las de\(X\).
Ejemplo\(\PageIndex{6}\)
Una variable aleatoria discreta\(X\) tiene la siguiente distribución de probabilidad:
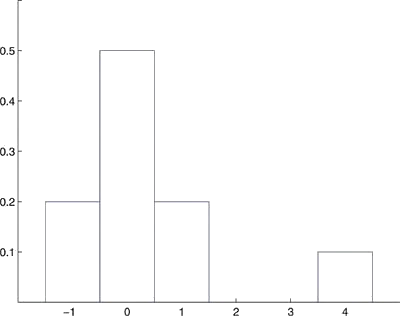
\[\begin{array}{c|cccc} x &-1 &0 &1 &4\\ \hline P(x) &0.2 &0.5 &a &0.1\\ \end{array} \label{Ex61}\]
Un histograma que ilustra gráficamente la distribución de probabilidad se da en la Figura\(\PageIndex{3}\).
Compute cada una de las siguientes cantidades.
- \(a\).
- \(P(0)\).
- \(P(X> 0)\).
- \(P(X\geq 0)\).
- \(P(X\leq -2)\).
- La media\(\mu \) de\(X\).
- La varianza\(\sigma ^2\) de\(X\).
- La desviación estándar\(\sigma \) de\(X\).
Solución:
- Dado que todas las probabilidades deben sumar hasta 1,\[a=1-(0.2+0.5+0.1)=0.2 \nonumber\]
- Directamente de la tabla, P (0) =0.5\[P(0)=0.5 \nonumber\]
- De la Tabla\ ref {Ex61},\[P(X> 0)=P(1)+P(4)=0.2+0.1=0.3 \nonumber\]
- De la Tabla\ ref {Ex61},\[P(X\geq 0)=P(0)+P(1)+P(4)=0.5+0.2+0.1=0.8 \nonumber\]
- Dado que ninguno de los números listados como posibles valores para\(X\) es menor o igual a\(-2\), el evento\(X\leq -2\) es imposible, por lo que\[P(X\leq -2)=0 \nonumber\]
- Usando la fórmula en la definición de\(\mu \) (Ecuación\ ref {media})\[\begin{align*}\mu &=\sum x P(x) \\[5pt] &=(-1)\cdot (0.2)+(0)\cdot (0.5)+(1)\cdot (0.2)+(4)\cdot (0.1) \\[5pt] &=0.4 \end{align*}\]
- Usando la fórmula en la definición de\(\sigma ^2\) (Ecuación\ ref {var1}) y el valor de\(\mu \) eso se acaba de calcular,\[\begin{align*} \sigma ^2 &=\sum (x-\mu )^2P(x) \\ &= (-1-0.4)^2\cdot (0.2)+(0-0.4)^2\cdot (0.5)+(1-0.4)^2\cdot (0.2)+(4-0.4)^2\cdot (0.1)\\ &= 1.84 \end{align*}\]
- Usando el resultado de la parte (g),\(\sigma =\sqrt{1.84}=1.3565\)
Resumen
- La distribución de probabilidad de una variable aleatoria discreta\(X\) es un listado de cada valor posible\(x\) tomado por\(X\) junto con la probabilidad\(P(x)\) que\(X\) toma ese valor en un ensayo del experimento.
- La media\(\mu \) de una variable aleatoria discreta\(X\) es un número que indica el valor promedio de\(X\) más de numerosos ensayos del experimento. Se calcula usando la fórmula\(\mu =\sum xP(x)\).
- La varianza\(\sigma ^2\) y desviación estándar\(\sigma \) de una variable aleatoria discreta\(X\) son números que indican la variabilidad de\(X\) más de numerosos ensayos del experimento. Se pueden computar usando la fórmula\(\sigma ^2=\left [ \sum x^2P(x) \right ]-\mu ^2\).

