5.1: Variables aleatorias continuas
- Page ID
- 151163
Objetivos de aprendizaje
- Conocer el concepto de distribución de probabilidad de una variable aleatoria continua, y cómo se utiliza para calcular probabilidades.
- Conocer datos básicos sobre la familia de variables aleatorias normalmente distribuidas.
La distribución de probabilidad de una variable aleatoria continua
Para una variable aleatoria discreta tiene sentido\(X\) la probabilidad de que\(X\) asuma uno de sus posibles valores en un solo ensayo del experimento. Este no es el caso de una variable aleatoria continua. Por ejemplo, supongamos\(X\) denota el tiempo que un viajante que acaba de llegar a una parada de autobús tiene que esperar al siguiente autobús. Si los autobuses funcionan cada\(30\) minuto sin falta, entonces el conjunto de valores posibles de\(X\) es el intervalo denotado\(\left [ 0,30 \right ]\), el conjunto de todos los números decimales entre\(0\) y\(30\). Pero aunque el número\(7.211916\) es un posible valor de\(X\), hay poco o ningún significado en el concepto de la probabilidad de que el habitante espere precisamente\(7.211916\) minutos para el próximo autobús. En todo caso la probabilidad debería ser cero, ya que si pudiéramos medir de manera significativa el tiempo de espera a la millonésima parte más cercana de minuto es prácticamente inconcebible que alguna vez obtengamos exactamente\(7.211916\) minutos. Las preguntas más significativas son las de la forma: ¿Cuál es la probabilidad de que el tiempo de espera del commuter sea menor que\(10\) minutos, o sea entre\(5\) y\(10\) minutos? En otras palabras, con variables aleatorias continuas uno se refiere no al evento de que la variable asume un único valor particular, sino con el evento de que la variable aleatoria asume un valor en un intervalo determinado.
Definición: función de densidad
La distribución de probabilidad de una variable aleatoria continua\(X\) es una asignación de probabilidades a intervalos de números decimales usando una función\(f(x)\), llamada función de densidad, de la siguiente manera: la probabilidad de que\(X\) asuma un valor en el intervalo\(\left [ a,b\right ]\) es igual a la área de la región que está delimitada arriba por la gráfica de la ecuación\(y=f(x)\), delimitada abajo por el eje x, y delimitada a la izquierda y derecha por las líneas verticales a través\(a\) y\(b\), como se ilustra en la Figura\(\PageIndex{1}\).
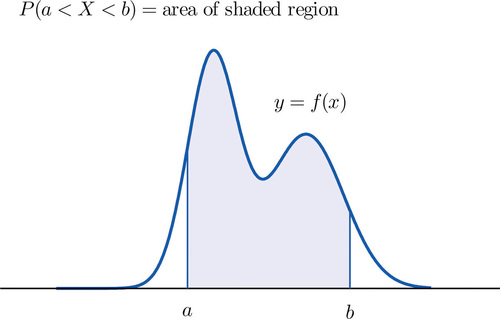
Esta definición puede entenderse como una consecuencia natural de la discusión en la Sección 2.1.3. Ahí vimos que si tenemos a la vista una población (o una muestra muy grande) y hacemos mediciones con mayor y mayor precisión, entonces a medida que las barras en el histograma de frecuencia relativa se vuelven sumamente finas sus lados verticales se fusionan y desaparecen, y lo que queda es solo la curva formada por sus cimas, como que se muestra en la Figura 2.1.5. Además el área total bajo la curva es\(1\), y la proporción de la población con mediciones entre dos números\(a\) y\(b\) es el área bajo la curva y entre\(a\) y\(b\), como se muestra en la Figura 2.1.6. Si pensamos en\(X\) como una medida a precisión infinita que surge de la selección de cualquier miembro de la población al azar, entonces\(P(a<X<b)\) es simplemente la proporción de la población con mediciones entre\(a\) y\(b\), la curva en el histograma de frecuencia relativa es la densidad función para\(X\), y llegamos a la definición justo arriba.
- Cada función de densidad\(f(x)\) debe cumplir las dos condiciones siguientes:
- Para todos los números\(x\),\(f(x)\geq 0\), para que la gráfica de\(y=f(x)\) nunca caiga por debajo del eje x.
- El área de la región bajo la gráfica de\(y=f(x)\) y por encima del\(x\) eje es\(1\).
Debido a que el área de un segmento de línea es\(0\), la definición de la distribución de probabilidad de una variable aleatoria continua implica que para cualquier número decimal en particular\(a\), digamos, la probabilidad que\(X\) asume el valor exacto a es\(0\). Esta propiedad implica que si se incluyen o no los puntos finales de un intervalo no hace diferencia con respecto a la probabilidad del intervalo.
Para cualquier variable aleatoria continua\(X\):
\[P(a\leq X\leq b)=P(a<X\leq b)=P(a\leq X<b)=P(a<X<b)\]
Ejemplo\(\PageIndex{1}\)
Una variable aleatoria\(X\) tiene la distribución uniforme en el intervalo\(\left [ 0,1\right ]\): la función de densidad es\(f(x)=1\) si\(x\) está entre\(0\) y\(1\) y\(f(x)=0\) para todos los demás valores de\(x\), como se muestra en la Figura\(\PageIndex{2}\).
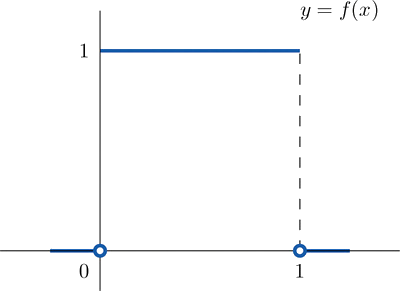
- Encontrar\(P(X > 0.75)\), la probabilidad de que\(X\) asuma un valor mayor que\(0.75\).
- Encontrar\(P(X \leq 0.2)\), la probabilidad de que\(X\) asuma un valor menor o igual a\(0.2\).
- Encontrar\(P(0.4 < X < 0.7)\), la probabilidad que\(X\) asume un valor entre\(0.4\) y\(0.7\).
Solución:
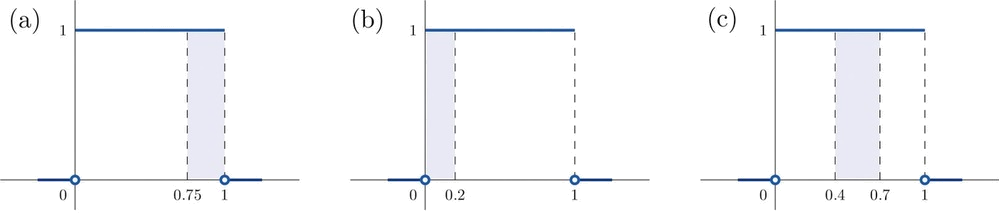
- \(P(X > 0.75)\)es el área del rectángulo de altura\(1\) y longitud de base\(1-0.75=0.25\), por lo tanto es\(base\times height=(0.25)\cdot (1)=0.25\). Ver Figura\(\PageIndex{3a}\).
- \(P(X \leq 0.2)\)es el área del rectángulo de altura\(1\) y longitud de base\(0.2-0=0.2\), por lo tanto es\(base\times height=(0.2)\cdot (1)=0.2\). Ver Figura\(\PageIndex{3b}\).
- \(P(0.4 < X < 0.7)\)es el área del rectángulo de altura\(1\) y longitud\(0.7-0.4=0.3\), por lo tanto es\(base\times height=(0.3)\cdot (1)=0.3\). Ver Figura\(\PageIndex{3c}\).
Ejemplo\(\PageIndex{2}\)
Un hombre llega a una parada de autobús a una hora aleatoria (es decir, sin tener en cuenta el servicio programado) para tomar el siguiente autobús. Los autobuses circulan cada\(30\) minuto sin falta, de ahí que el siguiente autobús llegue en cualquier momento durante los siguientes\(30\) minutos con probabilidad distribuida uniformemente (una distribución uniforme). Encuentra la probabilidad de que llegue un autobús en los próximos\(10\) minutos.
Solución:
El gráfico de la función de densidad es una línea horizontal por encima del intervalo de\(0\) a\(30\) y es el\(x\) eje -en todas partes. Dado que el área total bajo la curva debe ser\(1\), la altura de la línea horizontal es\(1/30\) (Figura\(\PageIndex{4}\)). La probabilidad buscada es\(P(0\leq X\leq 10)\) .Por definición, esta probabilidad es el área de la región rectangular delimitada arriba por la línea horizontal\(f(x)=1/30\), delimitada por debajo por el\(x\) eje -eje, delimitada a la izquierda por la línea vertical en\(0\) (el\(y\) eje -), y delimitada a la derecha por el línea vertical en\(10\). Esta es la región sombreada en la Figura\(\PageIndex{4}\). Su área es la base del rectángulo multiplicada por su altura,\((10)\cdot (1/30)=1/3\). Así\(P(0\leq X\leq 10)=1/3\).

Distribuciones normales
La mayoría de la gente ha oído hablar de la “curva de campana”. Es la gráfica de una función de densidad específica\(f(x)\) que describe el comportamiento de variables aleatorias continuas tan diferentes como las alturas de los seres humanos, la cantidad de un producto en un contenedor que fue llenado por una empaquetadora de alta velocidad, o las velocidades de las moléculas en un gas. La fórmula para\(f(x)\) contiene dos parámetros\(\mu\) y a los\(\sigma\) que se les puede asignar cualquier valor numérico específico, siempre y cuando\(\sigma\) sea positivo. No vamos a necesitar saber la fórmula para\(f(x)\), pero para los que están interesados es
\[f(x)=\frac{1}{\sqrt{2\pi \sigma ^2}}e^{-\frac{1}{2}(\mu -x)^2/\sigma ^2}\]
donde\(\pi \approx 3.14159\) y\(e\approx 2.71828\) es la base de los logaritmos naturales.
Cada elección diferente de valores numéricos específicos para el par\(\mu\) y\(\sigma\) da una curva de campana diferente. El valor de\(\mu\) determina la ubicación de la curva, como se muestra en la Figura\(\PageIndex{5}\). En cada caso la curva es simétrica aproximadamente\(\mu\).
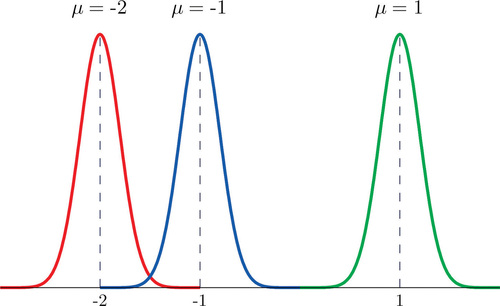
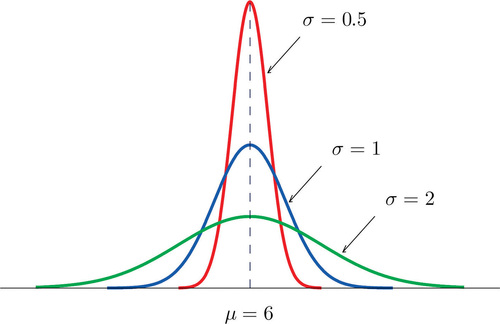
El valor de\(\sigma\) determina si la curva de campana es alta y delgada o corta y en cuclillas, sujeta siempre a la condición de que el área total bajo la curva sea igual a\(1\). Esto se muestra en la Figura\(\PageIndex{6}\), donde hemos elegido arbitrariamente centrar las curvas en\(\mu=6\).
Definición: distribución normal
La distribución de probabilidad correspondiente a la función de densidad para la curva de campana con parámetros\(\mu\) y\(\sigma\) se denomina distribución normal con media\(\mu\) y desviación estándar\(\sigma\).
Definición: variable aleatoria normalmente distribuida
Una variable aleatoria continua cuyas probabilidades se describen por la distribución normal con media\(\mu\) y desviación estándar\(\sigma\) se denomina variable aleatoria normalmente distribuida, o variable aleatoria normal para abreviar, con media\(\mu\) y desviación estándar\(\sigma\).
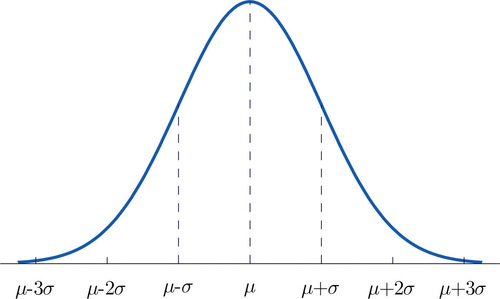
La figura\(\PageIndex{7}\) muestra la función de densidad que determina la distribución normal con media\(\mu\) y desviación estándar\(\sigma\). Repetimos un dato importante sobre esta curva: La curva de densidad para la distribución normal es simétrica con respecto a la media.
Ejemplo\(\PageIndex{3}\)
Las alturas\(25\) de los hombres de un año en cierta región tienen\(69.75\) pulgadas medias y pulgadas de desviación\(2.59\) estándar. Estas alturas están aproximadamente distribuidas normalmente. Así, la altura\(X\) de un hombre\(25\) de un año seleccionado al azar es una variable aleatoria normal con media\(\mu = 69.75\) y desviación estándar\(\sigma = 2.59\). Esboce un gráfico cualitativamente preciso de la función de densidad para\(X\). Encuentra la probabilidad de que un hombre de un\(25\) año seleccionado al azar tenga más de\(69.75\) centímetros de alto.
Solución:
La distribución de las alturas se parece a la curva de campana en la Figura\(\PageIndex{8}\). El punto importante es que está centrada en su media,\(69.75\), y es simétrica respecto a la media.
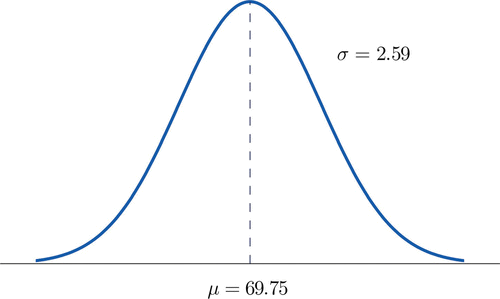
Dado que el área total bajo la curva es\(1\), por simetría el área a la derecha de\(69.75\) es la mitad del total, o\(0.5\). Pero esta área es precisamente la probabilidad\(P(X > 69.75)\), la probabilidad de que un hombre de un\(25\) año seleccionado al azar tenga más de\(69.75\) centímetros de alto. Aprenderemos a calcular otras probabilidades en las dos secciones siguientes.
Llave para llevar
- Para una variable aleatoria continua\(X\) las únicas probabilidades que se calculan son las de\(X\) tomar un valor en un intervalo especificado.
- La probabilidad de que\(X\) tome un valor en un intervalo determinado es la misma independientemente de que se incluyan o no los puntos finales del intervalo.
- La probabilidad\(P(a<X<b)\), que\(X\) tome un valor en el intervalo de\(a\) a\(b\), es el área de la región entre las líneas verticales a través\(a\) y\(b\), por encima del\(x\) eje, y por debajo de la gráfica de una función\(f(x)\) llamada función de densidad.
- Una variable aleatoria normalmente distribuida es aquella cuya función de densidad es una curva de campana.
- Cada curva de campana es simétrica con respecto a su media y se encuentra en todas partes por encima del\(x\) eje, al que se acerca asintóticamente (arbitrariamente de cerca sin tocar).

