8.4: Pruebas de muestra pequeña para una media poblacional
- Page ID
- 151143
Objetivos de aprendizaje
- Aprender a aplicar el procedimiento de prueba de cinco pasos para la prueba de hipótesis sobre una media poblacional cuando el tamaño de la muestra es pequeño.
En el apartado anterior se describieron las pruebas de hipótesis para las medias poblacionales en el caso de muestras grandes. La validez estadística de las pruebas fue asegurada por el Teorema del Límite Central, esencialmente sin suposiciones sobre la distribución de la población. Cuando los tamaños de muestra son pequeños, como suele ser el caso en la práctica, no se aplica el Teorema del Límite Central. Luego se deben imponer supuestos más estrictos a la población para dar validez estadística al procedimiento de prueba. Una suposición común es que la población de la que se toma la muestra tiene una distribución de probabilidad normal para empezar. En tales circunstancias, si se conoce la desviación estándar de la población, entonces el estadístico de prueba
\[\frac{(\bar{x}-\mu _0)}{\sigma /\sqrt{n}}\]
aún tiene la distribución normal estándar, como en las dos secciones anteriores. Si\(\sigma\) se desconoce y se aproxima por la desviación estándar de la muestra\(s\), entonces el estadístico de prueba resultante
\[\dfrac{(\bar{x}-\mu _0)}{s/\sqrt{n}}\]
sigue la\(t\) distribución de Student con\(n-1\) grados de libertad.
Estadísticas de pruebas estandarizadas para pruebas de hipótesis de muestra pequeña en relación con una media poblacional
Si\(\sigma\) se conoce:\[Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}}\]
Si\(\sigma\) se desconoce:\[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}\]
- El primer estadístico de prueba (\(\sigma\)conocido) tiene la distribución normal estándar.
- El segundo estadístico de prueba (\(\sigma\)desconocido) tiene la\(t\) distribución de Student con\(n-1\) grados de libertad.
- La población debe estar normalmente distribuida.
La distribución del segundo estadístico de prueba estandarizado (el que contiene\(s\)) y la región de rechazo correspondiente para cada forma de hipótesis alternativa (cola izquierda, cola derecha o dos colas), se muestra en la Figura\(\PageIndex{1}\). Esto es igual que la Figura 8.2.1 excepto que ahora los valores críticos son de la\(t\) distribución -. La Figura 8.2.1 todavía se aplica al primer estadístico de prueba estandarizado (el que contiene (\(\sigma\)) ya que sigue la distribución normal estándar.
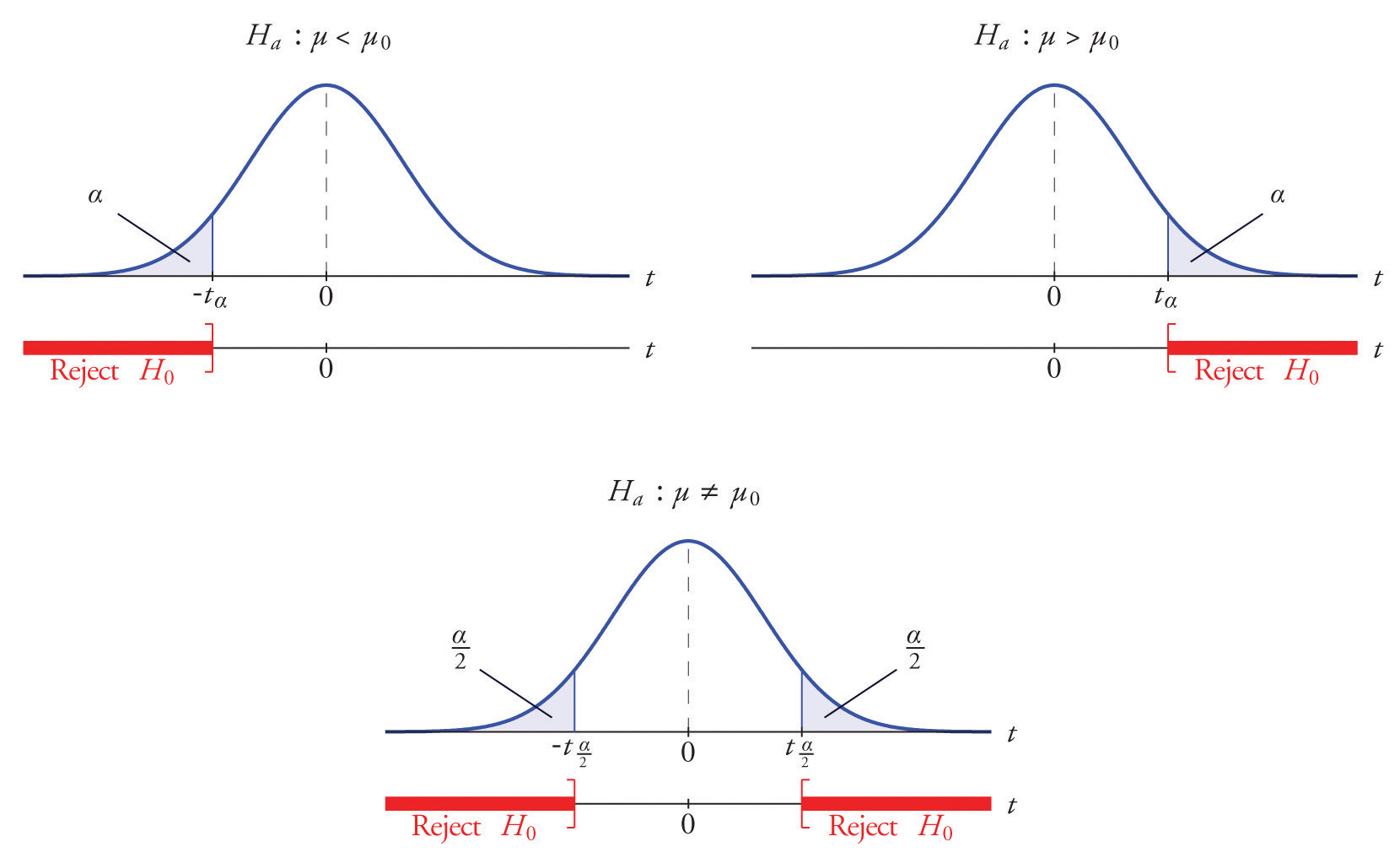
El\(p\) -valor de una prueba de hipótesis para la que el estadístico de prueba tiene la\(t\) distribución de Student puede calcularse utilizando software estadístico, pero no es práctico hacerlo usando tablas, ya que eso requeriría\(30\) tablas análogas a la Figura 7.1.5, una por cada grado de libertad de \(1\)a\(30\). La Figura 7.1.6 se puede utilizar para aproximar el\(p\) -valor de dicha prueba, y esto suele ser adecuado para tomar una decisión utilizando el enfoque\(p\) -value para la prueba de hipótesis, aunque no siempre. Por esta razón, las pruebas en los dos ejemplos de esta sección se realizarán siguiendo el enfoque de valor crítico para las pruebas de hipótesis resumido al final de la Sección 8.1, pero después de cada uno mostraremos cómo se pudo haber utilizado el enfoque\(p\) -value.
Ejemplo\(\PageIndex{1}\)
El precio de una raqueta de tenis popular en una cadena nacional de tiendas es\(\$179\). Portia compró cinco de la misma raqueta en un sitio de subastas en línea por los siguientes precios:
\[155\; 179\; 175\; 175\; 161\]
Suponiendo que los precios de subasta de raquetas se distribuyen normalmente, determinar si hay evidencia suficiente en la muestra, a\(5\%\) nivel de significación, para concluir que el precio promedio de la raqueta es menor que\(\$179\) si se compró en una subasta en línea.
Solución:
- Paso 1. La aseveración para la que se deben aportar pruebas es que el precio promedio en línea\(\mu\) es menor que el precio promedio en tiendas minoristas, por lo que la prueba de hipótesis es\[H_0: \mu =179\\ \text{vs}\\ H_a: \mu <179\; @\; \alpha =0.05\]
- Paso 2. La muestra es pequeña y se desconoce la desviación estándar poblacional. Así el estadístico de prueba es\[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}\] y tiene la\(t\) distribución Student con\(n-1=5-1=4\) grados de libertad.
- Paso 3. A partir de los datos calculamos\(\bar{x}=169\) y\(s=10.39\). Insertar estos valores en la fórmula para el estadístico de prueba da\[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}=\frac{169-179}{10.39/\sqrt{5}}=-2.152\]
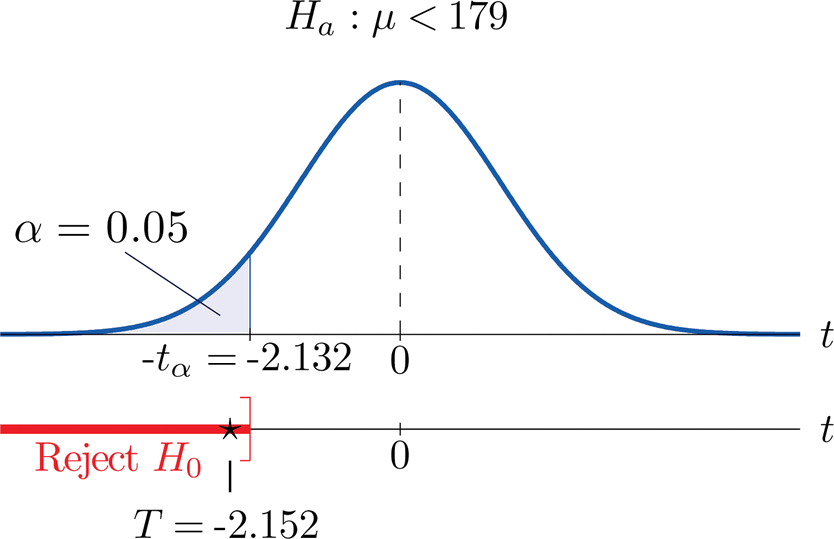
- Paso 4. Dado que el símbolo en\(H_a\) es “\(<\)” esta es una prueba de cola izquierda, por lo que hay un solo valor crítico,\(-t_\alpha =-t_{0.05}[df=4]\). Al leer de la fila etiquetada\(df=4\) en la Figura 7.1.6 su valor es\(-2.132\). La región de rechazo es\((-\infty ,-2.132]\).
- Paso 5. Como se muestra en\(\PageIndex{2}\) la Figura el estadístico de prueba cae en la región de rechazo. La decisión es rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos proporcionan evidencia suficiente, a\(5\%\) nivel de significancia, para concluir que el precio promedio de tales raquetas compradas en subastas en línea es menor que\(\$179\).
Para realizar la prueba en Ejemplo\(\PageIndex{1}\) usando el enfoque\(p\) -value, mire en la fila de la Figura 7.1.6 con el encabezado\(df=4\) y busque los dos\(t\) -valores que paréntesis el valor sin signo\(2.152\) del estadístico de prueba. Son\(2.132\) y\(2.776\), en las columnas con encabezamientos\(t_{0.050}\) y\(t_{0.025}\). Cortan colas derechas de área\(0.050\) y\(0.025\), así porque\(2.152\) está entre ellas debe cortar una cola de área entre\(0.050\) y\(0.025\). Por simetría\(-2.152\) corta una cola izquierda de área entre\(0.050\) y\(0.025\), de ahí el\(p\) -valor correspondiente a\(t=-2.152\) es entre\(0.025\) y\(0.05\). Si bien se desconoce su valor preciso, debe ser menor que\(\alpha =0.05\), por lo que la decisión es rechazar\(H_0\).
Ejemplo\(\PageIndex{2}\)
Un pequeño componente en un dispositivo electrónico tiene dos pequeños orificios donde se coloca otra parte diminuta. En el proceso de fabricación la distancia promedio entre los dos orificios debe controlarse estrechamente en\(0.02\) mm, de lo contrario muchas unidades serían defectuosas y desperdiciadas. Muchas veces a lo largo del día, los ingenieros de control de calidad toman una pequeña muestra de los componentes de la línea de producción, miden la distancia entre los dos orificios y realizan ajustes si es necesario. Supongamos que al mismo tiempo se toman cuatro unidades y las distancias se miden como
Determinar, a\(1\%\) nivel de significancia, si hay evidencia suficiente en la muestra para concluir que se necesita un ajuste. Supongamos que las distancias de interés se distribuyen normalmente.
Solución:
- Paso 1. El supuesto es que el proceso está bajo control a menos que haya pruebas contundentes de lo contrario. Dado que no es deseable una desviación de la distancia promedio a ambos lados, la prueba relevante es\[H_0: \mu =0.02\\ \text{vs}\\ H_a: \mu \neq 0.02\; @\; \alpha =0.01\] donde\(\mu\) denota la distancia media entre los agujeros.
- Paso 2. La muestra es pequeña y se desconoce la desviación estándar poblacional. Así el estadístico de prueba es\[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}\] y tiene la\(t\) distribución Student con\(n-1=4-1=3\) grados de libertad.
- Paso 3. A partir de los datos calculamos\(\bar{x}=0.02075\) y\(s=0.00171\). Insertar estos valores en la fórmula para el estadístico de prueba da\[T=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}=\frac{0.02075-0.02}{0.00171\sqrt{4}}=0.877\]
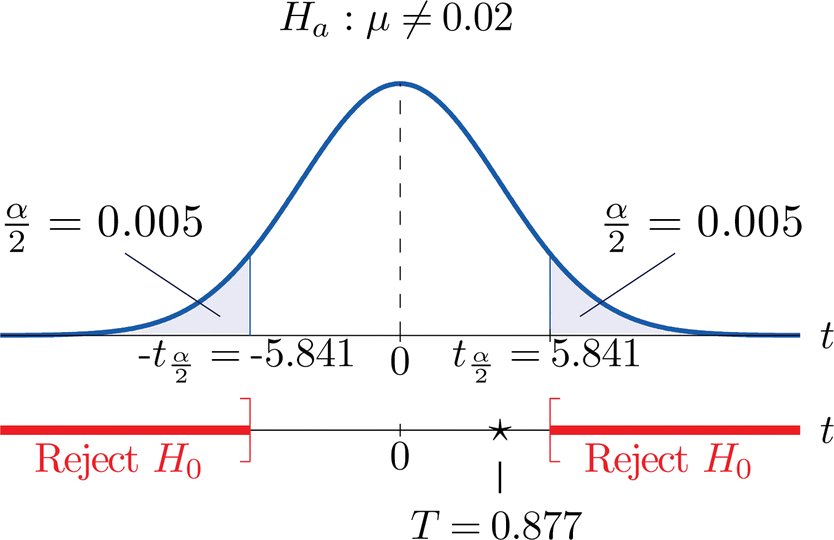
- Paso 4. Dado que el símbolo en\(H_a\) es “\(\neq\)” esta es una prueba de dos colas, por lo que hay dos valores críticos,\(\pm t_{\alpha/2} =-t_{0.005}[df=3]\). Leyendo de la fila en la Figura 7.1.6 etiquetada\(df=3\) sus valores son\(\pm 5.841\). La región de rechazo es\((-\infty ,-5.841]\cup [5.841,\infty )\).
- Paso 5. Como se muestra en\(\PageIndex{3}\) la Figura el estadístico de prueba no cae en la región de rechazo. La decisión es no rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos no proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que la distancia media entre los agujeros en el componente difiere de\(0.02\) mm.
Para realizar la prueba en “Ejemplo\(\PageIndex{2}\)" utilizando el enfoque\(p\) -value, busque en la fila de la Figura 7.1.6 con el encabezado\(df=3\) y busque los dos\(t\) -valores que paréntesis el valor\(0.877\) del estadístico de prueba. En realidad\(0.877\) es menor que el número más pequeño de la fila, que es\(0.978\), en la columna con encabezado\(t_{0.200}\). El valor\(0.978\) corta una cola derecha de área\(0.200\), por lo que debido a que\(0.877\) está a su izquierda debe cortar una cola de área mayor que\(0.200\). Así, el\(p\) -valor, que es el doble del área cortada (ya que la prueba es de dos colas), es mayor que\(0.400\). Si bien se desconoce su valor preciso, debe ser mayor que\(\alpha =0.01\), por lo que la decisión no es rechazar\(H_0\).
Llave para llevar
- Existen dos fórmulas para el estadístico de prueba en las hipótesis de prueba sobre una media poblacional con muestras pequeñas. Un estadístico de prueba sigue la distribución normal estándar, la otra\(t\) distribución de Student.
- Se utiliza la desviación estándar poblacional si se conoce, de lo contrario se utiliza la desviación estándar de la muestra.
- Ya sea el procedimiento de cinco pasos, el valor crítico o\(p\) el enfoque -valor, se utiliza con cualquiera de los dos estadísticos de prueba.

