8.5: Pruebas de muestra grande para una proporción poblacional
- Page ID
- 151142
Objetivos de aprendizaje
- Aprender a aplicar el procedimiento de prueba de valor crítico de cinco pasos para la prueba de hipótesis concernientes a una proporción poblacional.
- Aprender a aplicar el procedimiento de prueba de cinco pasos\(p\) -valor para la prueba de hipótesis concernientes a una proporción poblacional.
Tanto el enfoque de valor crítico como el enfoque de valor p se pueden aplicar para probar hipótesis sobre una proporción poblacional p. La hipótesis nula tendrá la forma\(H_0 : p = p_0\) para algún número específico\(p_0\) entre\(0\) y\(1\). La hipótesis alternativa será una de las tres desigualdades
- \(p <p_0\),
- \(p>p_0\), o
- \(p≠p_0\)
para el mismo número\(p_0\) que aparece en la hipótesis nula.
La información de la Sección 6.3 da la siguiente fórmula para el estadístico de prueba y su distribución. En la fórmula\(p_0\) está el valor numérico del\(p\) que aparece en las dos hipótesis,\(q_0=1−p_0, \hat{p}\) es la proporción muestral, y\(n\) es el tamaño de la muestra. Recuerde que la condición de que la muestra sea grande no es que\(n\) sea al menos 30 sino que el intervalo
\[ \left[ \hat{p} −3 \sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} , \hat{p} + 3 \sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} \right]\]
se encuentran completamente dentro del intervalo\([0,1]\).
Estadística de prueba estandarizada para pruebas de hipótesis de muestra grande en relación con una sola proporción de población
\[ Z = \dfrac{\hat{p} - p_0}{\sqrt{\dfrac{p_0q_o}{n}}} \label{eq2}\]
El estadístico de prueba tiene la distribución normal estándar.
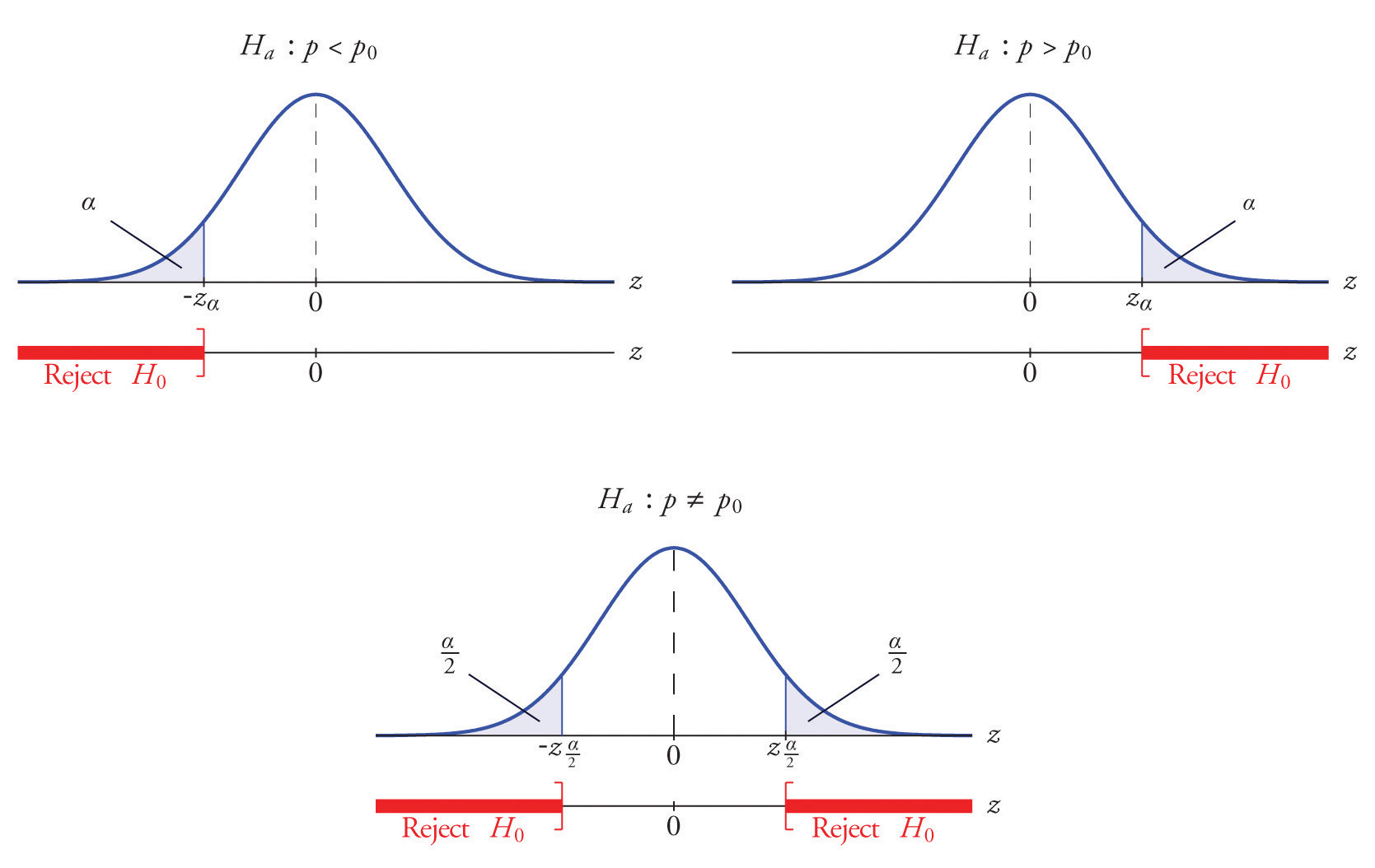
La distribución del estadístico de prueba estandarizado y la región de rechazo correspondiente para cada forma de hipótesis alternativa (cola izquierda, cola derecha o dos colas), se muestra en la Figura\(\PageIndex{1}\).
Ejemplo\(\PageIndex{1}\)
Un fabricante de refrescos afirma que la mayoría de los adultos prefieren su bebida principal sobre la de sus principales competidos.Para probar esta afirmación, las personas seleccionadas\(500\) al azar recibieron las dos bebidas en orden aleatorio al gusto. Entre ellos,\(270\) prefirieron la marca del fabricante de refrescos,\(211\) prefirieron la marca de la competencia y no\(19\) pudieron decidirse. Determinar si existe evidencia suficiente, a\(5\%\) nivel de significación, para sustentar la afirmación del fabricante de refrescos contra el incumplimiento de que la población está dividida equitativamente en su preferencia.
Solución:
Utilizaremos el enfoque de valor crítico para realizar la prueba. La misma prueba se realizará utilizando el enfoque\(p\) -value en Ejemplo\(\PageIndex{3}\).
Debemos verificar que la muestra sea lo suficientemente grande como para realizar válidamente la prueba. Dado que\(\hat{p} =270/500=0.54\),
\[\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} =\sqrt{ \dfrac{(0.54)(0.46)}{500}} ≈0.02\]de ahí
\[\begin{align} & \left[ \hat{p} −3\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} ,\hat{p} +3\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} \right] \\ &=[0.54−(3)(0.02),0.54+(3)(0.02)] \\ &=[0.48, 0.60] ⊂[0,1] \end{align}\]
por lo que la muestra es suficientemente grande.
- Paso 1. La prueba relevante es
\[H_0 : p = 0.50 \]
\[vs.\]
\[H_a : p > 0.50\, @ \,\alpha =0.05\]
donde\(p\) denota la proporción de todos los adultos que prefieren la bebida de la compañía sobre la de la bebida de su competidor.
- Paso 2. El estadístico de prueba (Ecuación\ ref {eq2}) es
\[Z=\dfrac{\hat{p} −p_0}{\sqrt{ \dfrac{p_0q_0}{n}}}\]
y tiene la distribución normal estándar.
- Paso 3. El valor del estadístico de prueba es
\[ \begin{align} Z &=\dfrac{\hat{p} −p_0}{\sqrt{ \dfrac{p_0q_0}{n}}} \\[6pt] &= \dfrac{0.54−0.50}{\sqrt{\dfrac{(0.50)(0.50)}{500}}} \\[6pt] &=1.789 \end{align} \]
- Paso 4. Dado que el símbolo en\(H_a\) es “\(>\)” esta es una prueba de cola derecha, por lo que hay un solo valor crítico,\(z_{α}=z_{0.05}\). Al leer desde la última línea de la Figura 7.1.6 su valor es\(1.645\). La región de rechazo es\([1.645,∞)\).
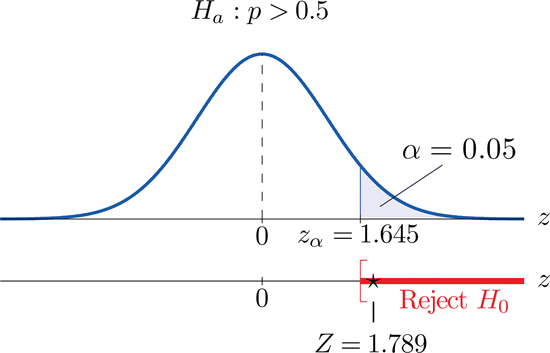
- Paso 5. Como se muestra en\(\PageIndex{2}\) la Figura el estadístico de prueba cae en la región de rechazo. La decisión es rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos proporcionan evidencia suficiente, a\(5\%\) nivel de significancia, para concluir que la mayoría de los adultos prefieren la bebida de la compañía a la de su competidor.
Ejemplo\(\PageIndex{2}\)
A nivel mundial la proporción a largo plazo de recién nacidos que son varones es\(51.46\%\). Un investigador considera que la proporción de niños al nacer cambia en condiciones económicas severas. Para probar esta creencia se examinaron registros de nacimiento seleccionados al azar de\(5,000\) bebés nacidos durante un periodo de recesión económica. Se encontró en la muestra que\(52.55\%\) de los recién nacidos eran niños. Determinar si existe evidencia suficiente, a\(10\%\) nivel de significación, para sustentar la creencia del investigador.
Solución:
Utilizaremos el enfoque de valor crítico para realizar la prueba. La misma prueba se realizará utilizando el enfoque\(p\) -value en Ejemplo\(\PageIndex{1}\).
La muestra es suficientemente grande para realizar válidamente la prueba ya que
\[\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} =\sqrt{ \dfrac{(0.5255)(0.4745)}{5000}} ≈0.01\]
de ahí
\[\begin{align} & \left[ \hat{p} −3\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} ,\hat{p} +3\sqrt{ \dfrac{\hat{p} (1−\hat{p} )}{n}} \right] \\ &=[0.5255−0.03,0.5255+0.03] \\ &=[0.4955,0.5555] ⊂[0,1] \end{align}\]
- Paso 1. \(p\)Sea la verdadera proporción de niños entre todos los recién nacidos durante el periodo de recesión. La carga de la prueba es demostrar que las severas condiciones económicas la cambian del valor histórico a largo plazo de\(0.5146\) más que demostrar que se mantiene igual, por lo que la prueba de hipótesis es
\[H_0 : p = 0.5146 \]
\[vs.\]
\[H_a : p \neq 0.5146\, @ \,\alpha =0.10\]
- Paso 2. El estadístico de prueba (Ecuación\ ref {eq2}) es
\[Z=\dfrac{\hat{p} −p_0}{\sqrt{ \dfrac{p_0q_0}{n}}}\]
y tiene la distribución normal estándar.
- Paso 3. El valor del estadístico de prueba es
\[ \begin{align} Z &=\dfrac{\hat{p} −p_0}{\sqrt{ \dfrac{p_0q_0}{n}}} \\[6pt] &= \dfrac{0.5255−0.5146}{\sqrt{\dfrac{(0.5146)(0.4854)}{5000}}} \\[6pt] &=1.542 \end{align} \]
- Paso 4. Dado que el símbolo en\(H_a\) es “\(\neq\)” esta es una prueba de dos colas, por lo que hay un par de valores críticos,\(\pm z_{\alpha /2}=\pm z_{0.05}=\pm 1.645\). La región de rechazo es\((-\infty ,-1.645]\cup [1.645,\infty )\).
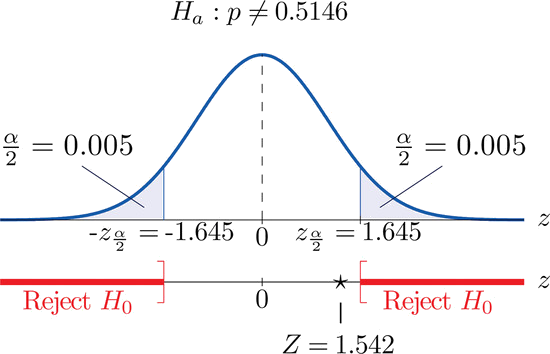
- Paso 5. Como se muestra en\(\PageIndex{3}\) la Figura el estadístico de prueba no cae en la región de rechazo. La decisión es no rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos no aportan evidencia suficiente, a\(10\%\) nivel de significancia, para concluir que la proporción de recién nacidos varones difiere de la proporción histórica en tiempos de recesión económica.
Ejemplo\(\PageIndex{3}\)
Realizar la prueba de Ejemplo\(\PageIndex{1}\) usando el enfoque\(p\) -value.
Solución:
Ya sabemos que el tamaño de la muestra es suficientemente grande para realizar válidamente la prueba.
- Los pasos 1—3 del procedimiento de cinco pasos descrito en la Sección 8.3 ya se han realizado en Ejemplo por\(\PageIndex{1}\) lo que no los repetiremos aquí, sino que solo decimos que sabemos que la prueba es de cola derecha y ese valor del estadístico de prueba es\(Z = 1.789\).
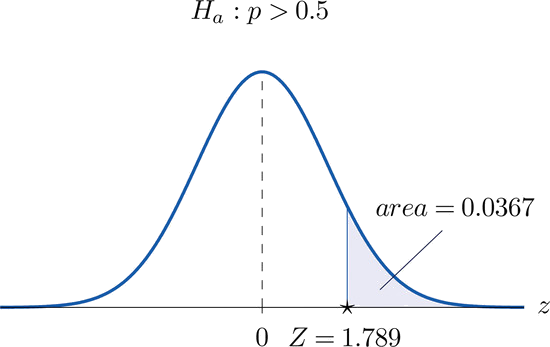
- Paso 4. Dado que la prueba es de cola derecha el valor p es el área bajo la curva normal estándar cortada por el estadístico de prueba observado,\(Z = 1.789\), como se ilustra en la Figura\(\PageIndex{4}\). Por la Figura 7.1.5 esa área y por lo tanto el valor p es\(1−0.9633=0.0367\).
- Paso 5. Ya que el\(p\) -valor es menor que\(α=0.05\) la decisión es rechazar\(H_0\).
Ejemplo\(\PageIndex{4}\)
Realizar la prueba de Ejemplo\(\PageIndex{2}\) usando el enfoque\(p\) -value.
Solución
Ya sabemos que el tamaño de la muestra es suficientemente grande para realizar válidamente la prueba.
- Los pasos 1—3 del procedimiento de cinco pasos descrito en la Sección 8.3 ya se han realizado en Ejemplo\(\PageIndex{2}\). Nos dicen que la prueba es de dos colas y que es el valor del estadístico de prueba\(Z = 1.542\).
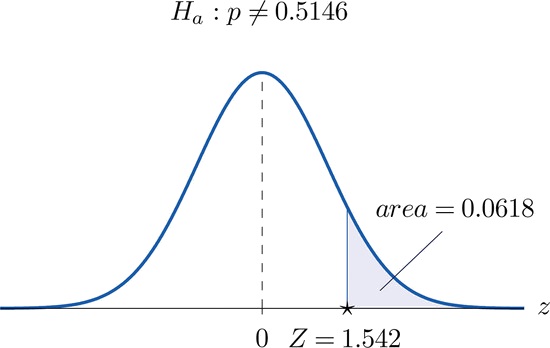
- Paso 4. Dado que la prueba es de dos colas el\(p\) -valor es el doble del área bajo la curva normal estándar cortada por el estadístico de prueba observado,\(Z = 1.542\). Por la Figura 7.1.5 esa área es\(1-0.9382=0.0618\), como se ilustra en la Figura\(\PageIndex{5}\), de ahí que el\(p\) -valor sea\(2\times 0.0618=0.1236\).
- Paso 5. Ya que el\(p\) -valor es mayor que\(\alpha =0.10\) la decisión no es rechazar\(H_0\).
Llave para llevar
- Hay una fórmula para el estadístico de prueba en las hipótesis de prueba sobre una proporción poblacional. El estadístico de prueba sigue la distribución normal estándar.
- Se puede utilizar el procedimiento de cinco pasos,\(p\) el valor crítico o el enfoque -value.

