9.1: Comparación de dos medias poblacionales: muestras grandes e independientes
- Page ID
- 151121
Objetivos de aprendizaje
- Comprender el marco lógico para estimar la diferencia entre las medias de dos poblaciones distintas y realizar pruebas de hipótesis sobre esas medias.
- Aprender a construir un intervalo de confianza para la diferencia en las medias de dos poblaciones distintas utilizando muestras grandes e independientes.
- Aprender a realizar una prueba de hipótesis sobre la diferencia entre las medias de dos poblaciones distintas utilizando muestras grandes e independientes.
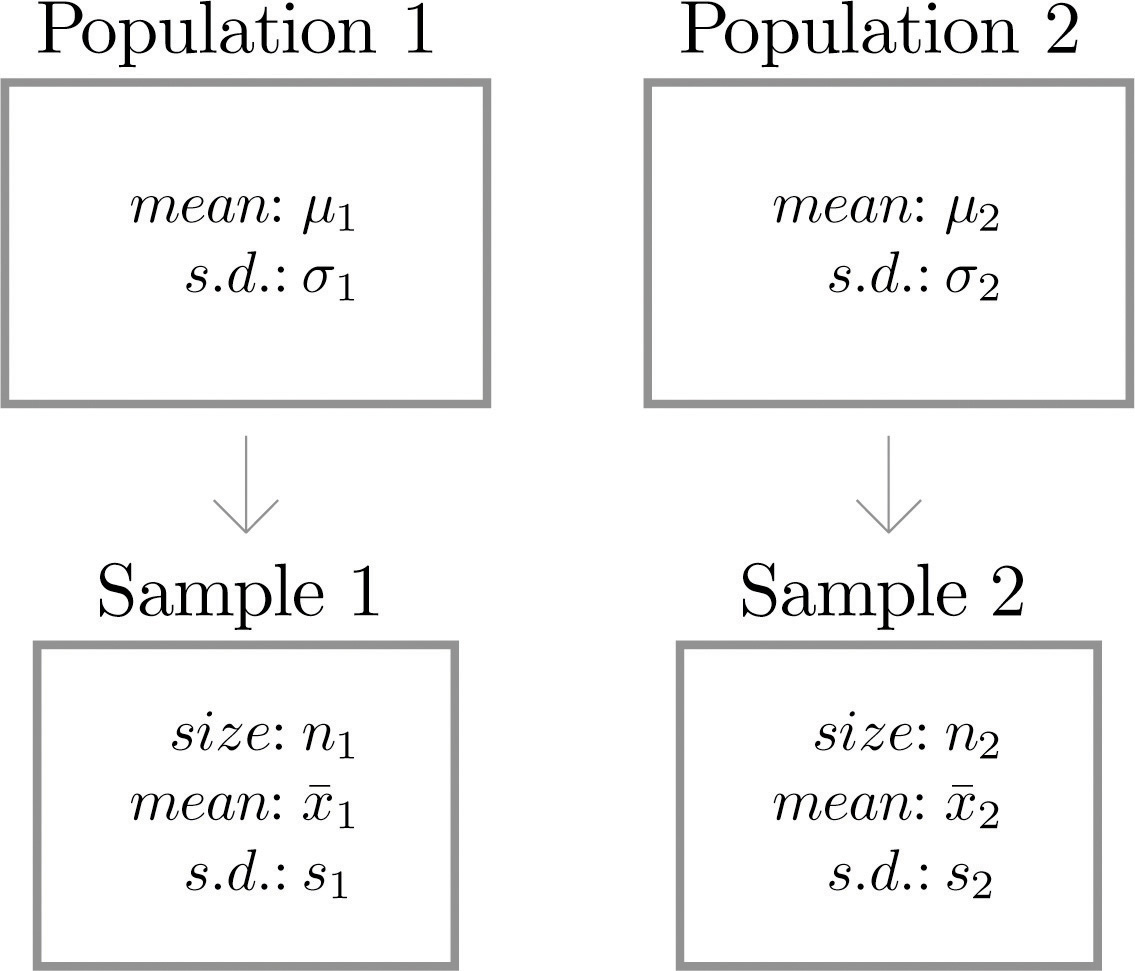
Supongamos que queremos comparar las medias de dos poblaciones distintas. La figura\(\PageIndex{1}\) ilustra el marco conceptual de nuestra investigación en esta y en la siguiente sección. Cada población tiene una media y una desviación estándar. Etiquetamos arbitrariamente una población como Población\(1\) y la otra como Población\(2\), y subindicamos los parámetros con los números\(1\) y\(2\) para diferenciarlos. Dibujamos una muestra aleatoria de Población\(1\) y etiquetamos los estadísticos de muestra que produce con el subíndice\(1\). Sin referencia a la primera muestra, extraemos una muestra de Población\(2\) y etiquetamos sus estadísticas de muestra con el subíndice\(2\).
Definición: Independencia
Las muestras de dos poblaciones distintas son independientes si cada una se dibuja sin referencia a la otra, y no tiene conexión con la otra.
Nuestro objetivo es utilizar la información de las muestras para estimar la diferencia\(\mu _1-\mu _2\) en las medias de las dos poblaciones y hacer inferencias estadísticamente válidas al respecto.
Intervalos de confianza
Dado que la media\(x-1\) de la muestra extraída de Población\(1\) es un buen estimador de\(\mu _1\) y la media\(x-2\) de la muestra extraída de Población\(2\) es un buen estimador de\(\mu _2\), una estimación puntual razonable de la diferencia\(\mu _1-\mu _2\) es\(\bar{x_1}-\bar{x_2}\). Para ensanchar esta estimación de punto en un intervalo de confianza, primero suponemos que ambas muestras son grandes, es decir, que ambas\(n_1\geq 30\) y\(n_2\geq 30\). Si es así, entonces la siguiente fórmula para un intervalo de confianza para\(\mu _1-\mu _2\) es válida. Los símbolos\(s_{1}^{2}\) y\(s_{2}^{2}\) denotan los cuadrados de\(s_1\) y\(s_2\). (En el caso relativamente raro de que tanto las desviaciones\(\sigma _1\) estándar poblacionales como\(\sigma _2\) se conozcan se utilizarían en lugar de las desviaciones estándar de la muestra).
\(100(1-\alpha )\%\)Intervalo de confianza para la diferencia entre dos medias poblacionales: muestras grandes e independientes
Las muestras deben ser independientes, y cada muestra debe ser grande:
Ejemplo\(\PageIndex{1}\)
Para comparar los niveles de satisfacción del cliente de dos compañías de televisión por cable competidoras,\(174\) los clientes de la Compañía\(1\)\(2\) y\(355\) los clientes de la Compañía fueron seleccionados al azar y se les pidió que calificaran sus compañías de cable en una escala de cinco puntos,\(1\) siendo menos satisfechos y \(5\)más satisfecho. Los resultados de la encuesta se resumen en la siguiente tabla:
| Empresa 1 | Empresa 2 |
|---|---|
| \(n_1=174\) | \(n_2=355\) |
| \(x-1=3.51\) | \(x-2=3.24\) |
| \(s_1=0.51\) | \(s_2=0.52\) |
Construir una estimación puntual y un intervalo de confianza del 99% para\(\mu _1-\mu _2\), la diferencia en los niveles de satisfacción promedio de los clientes de las dos empresas medidos en esta escala de cinco puntos.
Solución:
La estimación puntual de\(\mu _1-\mu _2\) es
\[\bar{x_1}-\bar{x_2}=3.51-3.24=0.27\]
En palabras, estimamos que el nivel promedio de satisfacción del cliente para la Compañía\(1\) es\(0.27\) puntos más alto en esta escala de cinco puntos que para la Compañía\(2\).
Para aplicar la fórmula para el intervalo de confianza, proceda exactamente como se hizo en el Capítulo 7. El nivel de\(99\%\) confianza significa\(\alpha =1-0.99=0.01\) eso para que\(z_{\alpha /2}=z_{0.005}\). De la Figura 7.1.6 “Valores Críticos de" leemos directamente eso\(z_{0.005}=2.576\). Así
\[(\bar{x_1}-\bar{x_2})\pm z_{\alpha /2}\sqrt{\frac{s_{1}^{2}}{n_1}+\frac{s_{2}^{2}}{n_2}}=0.27\pm 2.576\sqrt{\frac{0.51^{2}}{174}+\frac{0.52^{2}}{355}}=0.27\pm 0.12\]
Estamos\(99\%\) seguros de que la diferencia en las medias poblacionales radica en el intervalo\([0.15,0.39]\), en el sentido de que en el muestreo repetido\(99\%\) de todos los intervalos construidos a partir de la muestra los datos de esta manera contendrán\(\mu _1-\mu _2\). En el contexto del problema decimos que estamos\(99\%\) seguros de que el nivel promedio de satisfacción del cliente para la Compañía\(1\) es entre\(0.15\) y\(0.39\) puntos más alto, en esta escala de cinco puntos, que el de la Compañía\(2\).
Prueba de Hipótesis
Las hipótesis relativas a los tamaños relativos de las medias de dos poblaciones se prueban utilizando los mismos procedimientos de valor crítico y\(p\) -valor que se utilizaron en el caso de una sola población. Todo lo que se necesita es saber expresar las hipótesis nulas y alternativas y conocer la fórmula para el estadístico de prueba estandarizado y la distribución que sigue.
Las hipótesis nulas y alternativas siempre se expresarán en términos de la diferencia de las dos medias poblacionales. Así siempre se escribirá la hipótesis nula
\[H_0: \mu _1-\mu _2=D_0\]
donde\(D_0\) es un número que se deduce de la declaración de la situación. Como fue el caso de una sola población, la hipótesis alternativa puede tomar una de las tres formas, con la misma terminología:
| Forma de H a | Terminología |
|---|---|
| \(H_a: \mu _1-\mu _2<D_0\) | Cola izquierda |
| \(H_a: \mu _1-\mu _2>D_0\) | Cola derecha |
| \(H_a: \mu _1-\mu _2\neq D_0\) | Dos colas |
Siempre y cuando las muestras sean independientes y ambas sean grandes, la siguiente fórmula para el estadístico de prueba estandarizado es válida, y tiene la distribución normal estándar. (En el caso relativamente raro de que tanto las desviaciones\(\sigma _1\) estándar poblacionales como\(\sigma _2\) se conozcan se utilizarían en lugar de las desviaciones estándar de la muestra).
Estadístico de prueba estandarizado para pruebas de hipótesis sobre la diferencia entre dos medias poblacionales: muestras grandes e independientes
\[Z=\frac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{\frac{s_{1}^{2}}{n_1}+\frac{s_{2}^{2}}{n_2}}}\]
El estadístico de prueba tiene la distribución normal estándar.
Las muestras deben ser independientes, y cada muestra debe ser grande:\(n_1\geq 30\) y\(n_2\geq 30\).
Ejemplo\(\PageIndex{2}\)
Consulte Ejemplo\(\PageIndex{1}\) relativo a los niveles medios de satisfacción de los clientes de dos compañías competidoras de televisión por cable. Pruebe a\(1\%\) nivel de significancia si los datos proporcionan evidencia suficiente para concluir que la Compañía\(1\) tiene una calificación media de satisfacción más alta que la Compañía\(2\). Utilizar el enfoque de valor crítico.
Solución:
- Paso 1. Si los niveles medios de satisfacción\(\mu _1\) y\(\mu _2\) son los mismos entonces\(\mu _1=\mu _2\), pero siempre expresamos la hipótesis nula en términos de la diferencia entre\(\mu _1\) y\(\mu _2\), por lo tanto\(H_0\) es\(\mu _1-\mu _2=0\). Decir que la satisfacción media del cliente para la Compañía\(1\) es mayor que la de la Compañía\(2\) significa eso\(\mu _1>\mu _2\), que en términos de su diferencia lo es\(\mu _1-\mu _2>0\). Por lo tanto, la prueba es
\[H_0: \mu _1-\mu _2=0\]
\[vs.\]
\[H_a: \mu _1-\mu _2>0\; \; @\; \; \alpha =0.01\]
- Paso 2. Dado que las muestras son independientes y ambas son grandes, el estadístico de prueba es
\[Z=\frac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{\frac{s_{1}^{2}}{n_1}+\frac{s_{2}^{2}}{n_2}}}\]
- Paso 3. Insertar los datos en la fórmula para el estadístico de prueba da
\[Z=\frac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{\frac{s_{1}^{2}}{n_1}+\frac{s_{2}^{2}}{n_2}}}=\frac{(3.51-3.24)-0}{\sqrt{\frac{0.51^{2}}{174}+\frac{0.52^{2}}{355}}}=5.684\]
- Paso 4. Dado que el símbolo en\(H_a\) es “\(>\)” esta es una prueba de cola derecha, por lo que hay un solo valor crítico,\(z_\alpha =z_{0.01}\), que a partir de la última línea en la Figura 7.1.6 “Valores críticos de" leemos como\(2.326\). La región de rechazo es\([2.326,\infty )\).
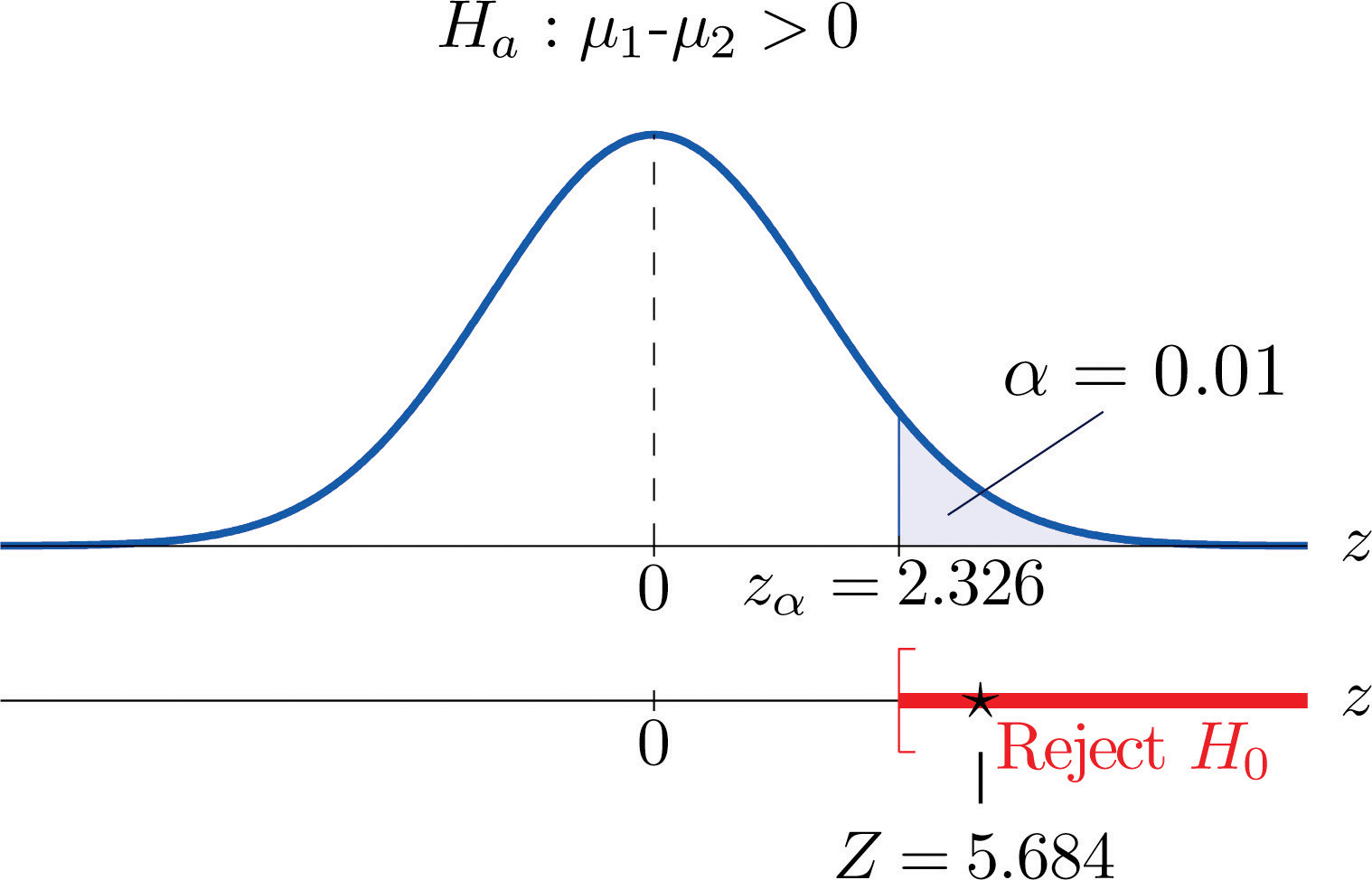
Figura\(\PageIndex{2}\): Región de rechazo y estadística de prueba por ejemplo\(\PageIndex{2}\)
-
Paso 5. Como se muestra en\(\PageIndex{2}\) la Figura el estadístico de prueba cae en la región de rechazo. La decisión es rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que la satisfacción media del cliente para la Compañía\(1\) es mayor que la de la Compañía\(2\).
Ejemplo\(\PageIndex{3}\)
Realice la prueba de Ejemplo\(\PageIndex{2}\) usando el\(p\)-value approach.
Solución:
Los tres primeros pasos son idénticos a los del Ejemplo\(\PageIndex{2}\)
- Paso 4. La significación observada o\(p\)-value of the test is the area of the right tail of the standard normal distribution that is cut off by the test statistic \(Z=5.684\). The number \(5.684\) is too large to appear in Figure 7.1.5, which means that the area of the left tail that it cuts off is \(1.0000\) to four decimal places. The area that we seek, the area of the right tail, is therefore \(1-1.0000=0.0000\) to four decimal places. See Figure \(\PageIndex{3}\). Es decir,\(p\)-value=\(0.0000\) to four decimal places. (The actual value is approximately \(0.000000007\).)
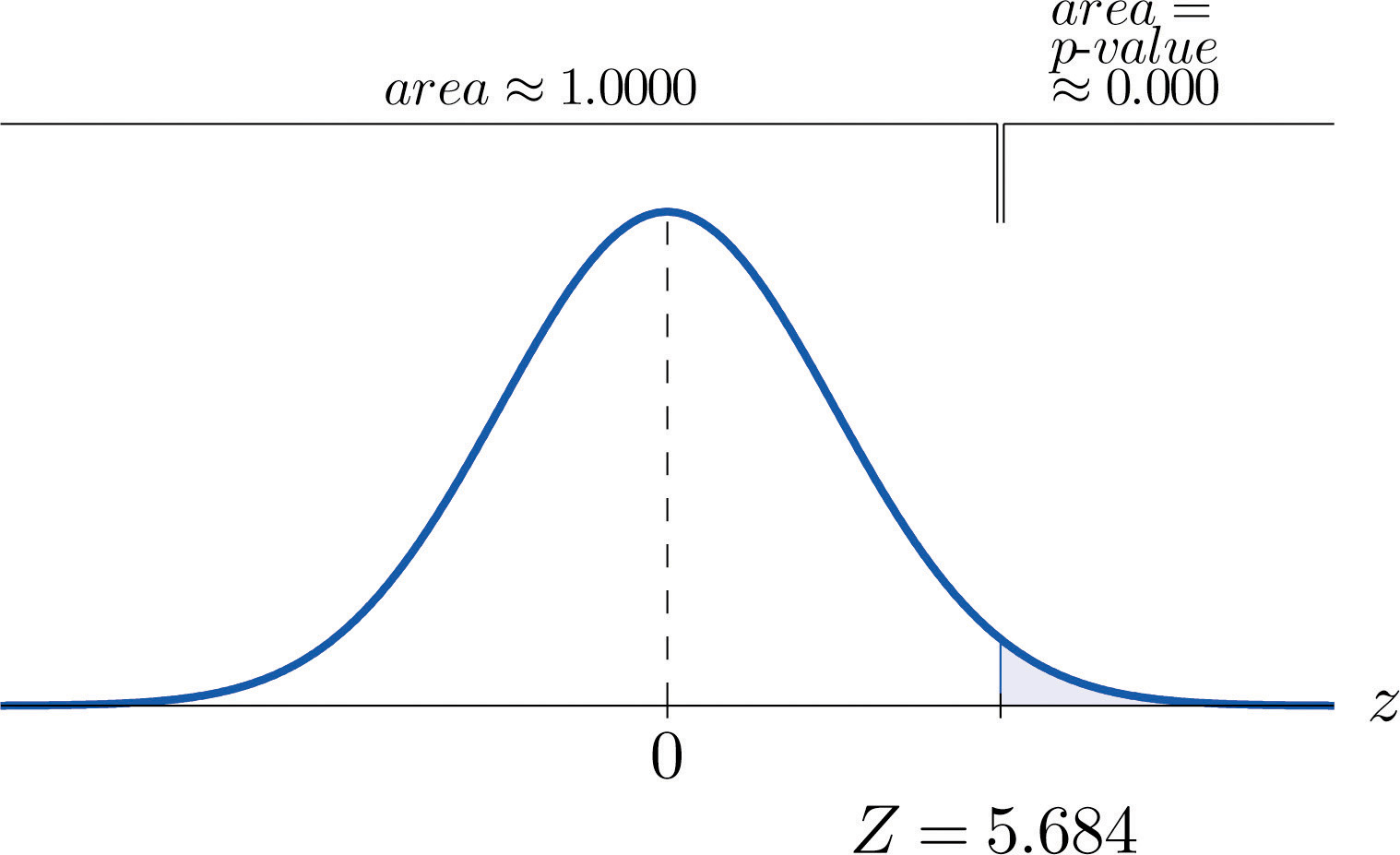
-
Paso 5. Ya\(p-value <\alpha\) que\(0.0000<0.01\), así la decisión es rechazar la hipótesis nula:
Los datos proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que la satisfacción media del cliente para la Compañía\(1\) es mayor que la de la Compañía\(2\).
Llave para llevar
- Una estimación puntual para la diferencia en dos medias poblacionales es simplemente la diferencia en las medias muestrales correspondientes.
- En el contexto de estimar o probar hipótesis relativas a dos medias poblacionales, las muestras “grandes” significan que ambas muestras son grandes.
- Se calcula un intervalo de confianza para la diferencia en dos medias poblacionales utilizando una fórmula de la misma manera que se hizo para una sola media poblacional.
- El mismo procedimiento de cinco pasos utilizado para probar hipótesis relativas a una sola media poblacional se utiliza para probar hipótesis sobre la diferencia entre dos medias poblacionales. La única diferencia está en la fórmula para el estadístico de prueba estandarizado.

