9.4: Comparación de dos proporciones poblacionales
- Page ID
- 151128
Objetivos de aprendizaje
- Aprender a construir un intervalo de confianza para la diferencia en las proporciones de dos poblaciones distintas que tienen una característica particular de interés.
- Aprender a realizar una prueba de hipótesis sobre la diferencia en las proporciones de dos poblaciones distintas que tienen una característica particular de interés.
Supongamos que deseamos comparar las proporciones de dos poblaciones que tienen una característica específica, como la proporción de hombres zurdos en comparación con la proporción de mujeres que son zurdas. La figura\(\PageIndex{1}\) ilustra el marco conceptual de nuestra investigación. Cada población se divide en dos grupos, el grupo de elementos que tienen la característica de interés (por ejemplo, ser zurdos) y el grupo de elementos que no lo tienen. Clasificamos arbitrariamente una población como Población\(1\) y la otra como Población\(2\), y subindicamos la proporción de cada población que posee la característica con el número\(1\) o\(2\) para diferenciarlos. Dibujamos una muestra aleatoria de Población\(1\) y etiquetamos el estadístico muestral que produce con el subíndice\(1\). Sin referencia a la primera muestra, dibujamos una muestra de Población\(2\) y etiquetamos su estadística de muestra con el subíndice\(2\).
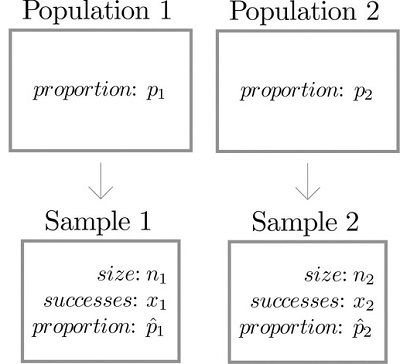
Nuestro objetivo es utilizar la información de las muestras para estimar la diferencia\(p_1-p_2\) en las dos proporciones poblacionales y hacer inferencias estadísticamente válidas al respecto.
Intervalos de confianza
Dado que la proporción muestral\(\hat{p}_1\) calculada utilizando la muestra extraída de Población\(1\) es un buen estimador de la proporción poblacional\(p_1\) de Población\(1\) y la proporción muestral\(\hat{p}_2\) calculada utilizando la muestra extraída de Población\(2\) es un buen estimador de población proporción\(p_2\) de Población\(2\), una estimación puntual razonable de la diferencia\(p_1−p_2\) es\(\hat{p}_1 -\hat{p}_2\). Para ensanchar esta estimación puntual en un intervalo de confianza suponemos que ambas muestras son grandes, como se describe en la Sección 7.3 y se repite a continuación. Si es así, entonces la siguiente fórmula para un intervalo de confianza para\(p_1−p_2\) es válida.
\(100(1−\alpha)\%\) Confidence Interval for the Difference Between Two Population Proportions
\[(\hat{p}_1−\hat{p}_2) \pm z_{a/2} \sqrt{ \dfrac{ \hat{p}_1(1−\hat{p}_1)}{n_1}+ \dfrac{\hat{p}_2(1−\hat{p}_2)}{n_2}}\]
Las muestras deben ser independientes, y cada muestra debe ser grande: cada uno de los intervalos
\[\left[ \hat{p}_1−3 \sqrt{ \dfrac{\hat{p}_1(1−\hat{p}_1)}{n_1}}, \hat{p}_1 + 3 \sqrt{ \dfrac{ \hat{p}_1(1−\hat{p}_1)}{n_1}} \right] \]
y
\[\left[ \hat{p}_2−3 \sqrt{ \dfrac{\hat{p}_2(1−\hat{p}_2)}{n_2}}, \hat{p}_2 + 3 \sqrt{ \dfrac{ \hat{p}_2(1−\hat{p}_2)}{n_2}} \right] \]
debe estar completamente dentro del intervalo\([0,1]\).
Ejemplo\(\PageIndex{1}\)
El departamento de cumplimiento de código de un gobierno de condado emite permisos a contratistas generales para trabajar en proyectos residenciales. Por cada permiso expedido, el departamento inspecciona el resultado del proyecto y otorga una calificación de “pase” o “falla”. Un proyecto fallido debe ser reinspeccionado hasta que reciba una calificación de aprobación. El departamento se había visto frustrado por el alto costo de la reinspección y decidió publicar en la web los registros de inspección de todos los contratistas. Se esperaba que el acceso público a los registros disminuyera la tasa de reinspección. Un año después de que se hiciera público el acceso a la web, se seleccionaron aleatoriamente dos muestras de registros. Se seleccionó una muestra del conjunto de registros antes de la publicación en la web y otra después. Se anotó la proporción de proyectos que pasaron la primera inspección para cada muestra. Los resultados se resumen a continuación. Construir una estimación puntual y un intervalo de\(90\%\) confianza para la diferencia en la tasa de aprobación en la primera inspección entre los dos periodos de tiempo.
\[\begin{array}{c|c} \text{No public web access} & n_1=500\; \; \hat{p_1}=0.67 \\ \hline \text{Public web access} & n_2=100\; \; \hat{p_2}=0.80 \\ \end{array}\]
Solución
La estimación puntual de\(p_1−p_2\) es
\[\hat{p}_1−\hat{p}_2=0.67−0.80=−0.13\]
Debido a que la población “Sin acceso a la web pública” fue etiquetada como Población\(1\) y la población “Acceso web público” fue etiquetada como Población\(2\), en palabras esto significa que estimamos que la proporción de proyectos que pasaron la primera inspección aumentó en puntos\(13\) porcentuales después de que los registros se publicaran en la web.
Los tamaños de muestra son suficientemente grandes para construir un intervalo de confianza ya que para la muestra 1:
\[ 3 \sqrt{ \dfrac{ \hat{p}_1(1−\hat{p}_1)}{n_1}} = 3 \sqrt{ \dfrac{ (0.67)(0.33)}{500}} =0.06\]
para que
\[\left [ \hat{p_1}-3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}}, \hat{p_1}+3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}} \right ]=[0.67-0.06,0.67+0.06]=[0.61,0.73]\subset [0,1]\]
y para la muestra\(2\):
\[3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}}=3\sqrt{\frac{(0.8)(0.2)}{100}}=0.12\]
para que
\[\left [ \hat{p_2}-3\sqrt{\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}, \hat{p_2}+3\sqrt{\frac{\hat{p_2}(1-\hat{p_2})}{n_2}} \right ]=[0.8-0.12,0.8+0.12]=[0.68,0.92]\subset [0,1]\]
Para aplicar la fórmula para el intervalo de confianza, primero observamos que el nivel de\(90\%\) confianza significa\(\alpha =1-0.90=0.10\) eso para que\(z_{\alpha /2}=z_{0.05}\). De la Figura 7.1.6 leemos directamente eso\(z_{0.05}=1.645\). Por lo tanto, el intervalo de confianza deseado es
\[\begin{align} (\hat{p}_1−\hat{p}_2)&± z_{α/2} \sqrt{ \dfrac{ \hat{p}_1(1−\hat{p}_1)}{n_1} + \dfrac{\hat{p}_2(1−\hat{p}_2)}{n_2}} \\ &= 0.13 ± 1.645 \sqrt{ \dfrac{(0.67)(0.33)}{500}+\dfrac{(0.8)(0.2)}{100}} \\ &= -0.13±0.07 \end{align}\]
El intervalo de\(90\%\) confianza es\([-0.20,-0.06]\). \(90\%\)Confiamos en que la diferencia en las proporciones poblacionales radica en el intervalo\([-0.20,-0.06]\), en el sentido de que en el muestreo repetido\(90\%\) de todos los intervalos construidos a partir de la muestra los datos de esta manera contendrán\(p_1−p_2\). Teniendo en cuenta el etiquetado de las dos poblaciones, esto significa que\(90\%\) confiamos en que la proporción de proyectos que pasan la primera inspección es entre\(6\) y puntos\(20\) porcentuales mayor después del acceso público a los registros que antes.
Prueba de Hipótesis
En las pruebas de hipótesis relativas a los tamaños relativos\(p_2\) de las proporciones\(p_1\) y de dos poblaciones que poseen una característica particular, las hipótesis nula y alternativa siempre se expresarán en términos de la diferencia de las dos proporciones poblacionales. De ahí que siempre se escriba la hipótesis nula
\[H_0: p_1−p_2=D_0\]
Las tres formas de la hipótesis alternativa, con la terminología para cada caso, son:
| Forma de\(H_a\) | Terminología |
|---|---|
| \ (H_a\) ">\(H_a : p _1−p_2 < D_0\) | Cola izquierda |
| \ (H_a\) ">\(H_a : p_1−p_2>D_0\) | Cola derecha |
| \ (H_a\) ">\(H_a : p_1−p_2 \neq D_0\) | Dos colas |
Siempre y cuando las muestras sean independientes y ambas sean grandes, la siguiente fórmula para el estadístico de prueba estandarizado es válida, y tiene la distribución normal estándar.
Estadístico de prueba estandarizado para pruebas de hipótesis sobre la diferencia entre dos proporciones de población
\[Z=\frac{(\hat{p_1}-\hat{p_2})-D_0}{\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}}\]
El estadístico de prueba tiene la distribución normal estándar.
Las muestras deben ser independientes, y cada muestra debe ser grande: cada uno de los intervalos
\[\left [ \hat{p_1}-3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}}, \hat{p_1}+3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}} \right ]\]
y
\[\left [ \hat{p_2}-3\sqrt{\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}, \hat{p_2}+3\sqrt{\frac{\hat{p_2}(1-\hat{p_2})}{n_2}} \right ]\]
debe estar completamente dentro del intervalo\([0,1]\).
Ejemplo\(\PageIndex{2}\)
Utilizando los datos de Ejemplo\(\PageIndex{1}\), pruebe si existe evidencia suficiente para concluir que el acceso web público a los registros de inspección ha aumentado la proporción de proyectos que pasaron en la primera inspección en más de puntos\(5\) porcentuales. Utilizar el enfoque de valor crítico a\(10\%\) nivel de significancia.
Solución:
- Paso 1. Teniendo en cuenta el etiquetado de las poblaciones se puede expresar como un incremento en la tasa de aprobación en la primera inspección en más de puntos\(5\) porcentuales después del acceso público en la web\(p_2>p_1+0.05\), que por álgebra es lo mismo que\(p_1-p_2<-0.05\). Esta es la hipótesis alternativa. Dado que la hipótesis nula siempre se expresa como una igualdad, con el mismo número a la derecha que en la hipótesis alternativa, la prueba es
\[H_0: p_1-p_2=-0.05\\ \text{vs.}\\ H_a: p_1-p_2<-0.05\; \; @\; \; \alpha =0.10\]
- Paso 2. Dado que la prueba es con respecto a una diferencia en las proporciones de la población, el estadístico de la prueba es
\[Z=\frac{(\hat{p_1}-\hat{p_2})-D_0}{\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}}\]
- Paso 3. Insertar los valores dados en Ejemplo\(\PageIndex{1}\) y el valor\(D_0=-0.05\) en la fórmula para el estadístico de prueba da
\[Z=\frac{(\hat{p_1}-\hat{p_2})-D_0}{\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}}=\frac{(-0.13)-(-0.05)}{\sqrt{\frac{(0.67)(0.33)}{500}+\frac{(0.8)(0.2)}{100}}}=-1.770\]
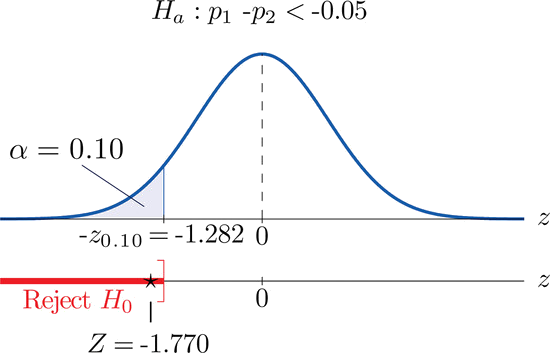
- Paso 4. Dado que el símbolo en\(H_a\) es “\(<\)” esta es una prueba de cola izquierda, por lo que hay un solo valor crítico,\(z_\alpha =-z_{0.10}\). De la última fila de la Figura 7.1.6\(z_{0.10}=1.282\), así\(-z_{0.10}=-1.282\). La región de rechazo es\((-\infty ,-1.282]\).
- Paso 5. Como se muestra en\(\PageIndex{2}\) la Figura el estadístico de prueba cae en la región de rechazo. La decisión es rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos proporcionan evidencia suficiente, a\(10\%\) nivel de significancia, para concluir que la tasa de paso en la primera inspección ha aumentado en más de puntos\(5\) porcentuales desde que los registros fueron publicados públicamente en la web.
Ejemplo\(\PageIndex{3}\)
Realizar la prueba de Ejemplo\(\PageIndex{2}\) usando el enfoque\(p\) -value.
Solución:
Los tres primeros pasos son idénticos a los del Ejemplo\(\PageIndex{2}\)
- Paso 4. Debido a que la prueba es de cola izquierda, la significancia observada o\(p\) -valor de la prueba es solo el área de la cola izquierda de la distribución normal estándar que es cortada por el estadístico de prueba\(Z=-1.770\). De la Figura 7.1.5 el área de la cola izquierda determinada por\(-1.77\) es\(0.0384\). El\(p\) -valor es\(0.0384\).
- Paso 5. Dado que el\(p\) -valor\(0.0384\) es menor que\(\alpha =0.10\), la decisión es rechazar la hipótesis nula: Los datos proporcionan evidencia suficiente, a\(10\%\) nivel de significancia, para concluir que la tasa de paso en la primera inspección ha aumentado en más de puntos\(5\) porcentuales ya que los registros se publicaron en la web.
Por último, hay que mencionar un mal uso común de las fórmulas dadas en esta sección. Supongamos que se realiza una gran encuesta preelectoral de votantes potenciales. A cada persona encuestada se le pide que exprese una preferencia entre, digamos, Candidato\(A\) y Candidato\(B\). (Quizás “ninguna preferencia” u “otra” también son opciones, pero eso no es importante). En dicha encuesta, los estimadores\(\hat{p}_A\) y\(\hat{p}B\) de\(p_A\) y\(p_B\) pueden ser calculados. Es importante darse cuenta, sin embargo, que estos dos estimadores no fueron calculados a partir de dos muestras independientes. Si bien\(\hat{p}A−\hat{p}_B\) puede ser un estimador razonable de\(p_A−p_B\), las fórmulas para intervalos de confianza y para el estadístico de prueba estandarizado que se dan en esta sección no son válidas para los datos obtenidos de esta manera.
Llave para llevar
- Se calcula un intervalo de confianza para la diferencia en dos proporciones poblacionales utilizando una fórmula de la misma manera que se hizo para una sola media poblacional.
- El mismo procedimiento de cinco pasos utilizado para probar hipótesis relativas a una sola proporción poblacional se utiliza para probar hipótesis sobre la diferencia entre dos proporciones de población. La única diferencia está en la fórmula para el estadístico de prueba estandarizado.

