10.1: Relaciones lineales entre variables
- Page ID
- 151177
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
Aprender lo que significa para dos variables exhibir una relación cercana a lineal, pero que contiene un elemento de aleatoriedad
La siguiente tabla da ejemplos de los tipos de pares de variables que podrían ser de interés desde el punto de vista estadístico.
| \(x\) | \(y\) |
|---|---|
| Predictor o variable independiente | Respuesta o variable dependiente |
| Temperatura en grados Celsius | Temperatura en grados Fahrenheit |
| Área de una casa (pies cuadrados) | Valor de la casa |
| Edad de una marca y modelo de automóvil en particular | Valor de reventa del auto |
| Cantidad gastada por una empresa en publicidad en un año | Ingresos recibidos ese año |
| Altura de un hombre\(25\) de un año | Peso del hombre |
La primera línea de la tabla es diferente de todas las demás porque en ese caso y en ningún otro la relación entre las variables es determinista: una vez que\(x\) se conoce el valor de\(y\) se determina completamente el valor de. De hecho existe una fórmula para\(y\) en términos de\(x\):
\[y=95x+32\]
Elegir varios valores para\(x\) y calcular el valor correspondiente\(y\) para cada uno usando la fórmula da la tabla
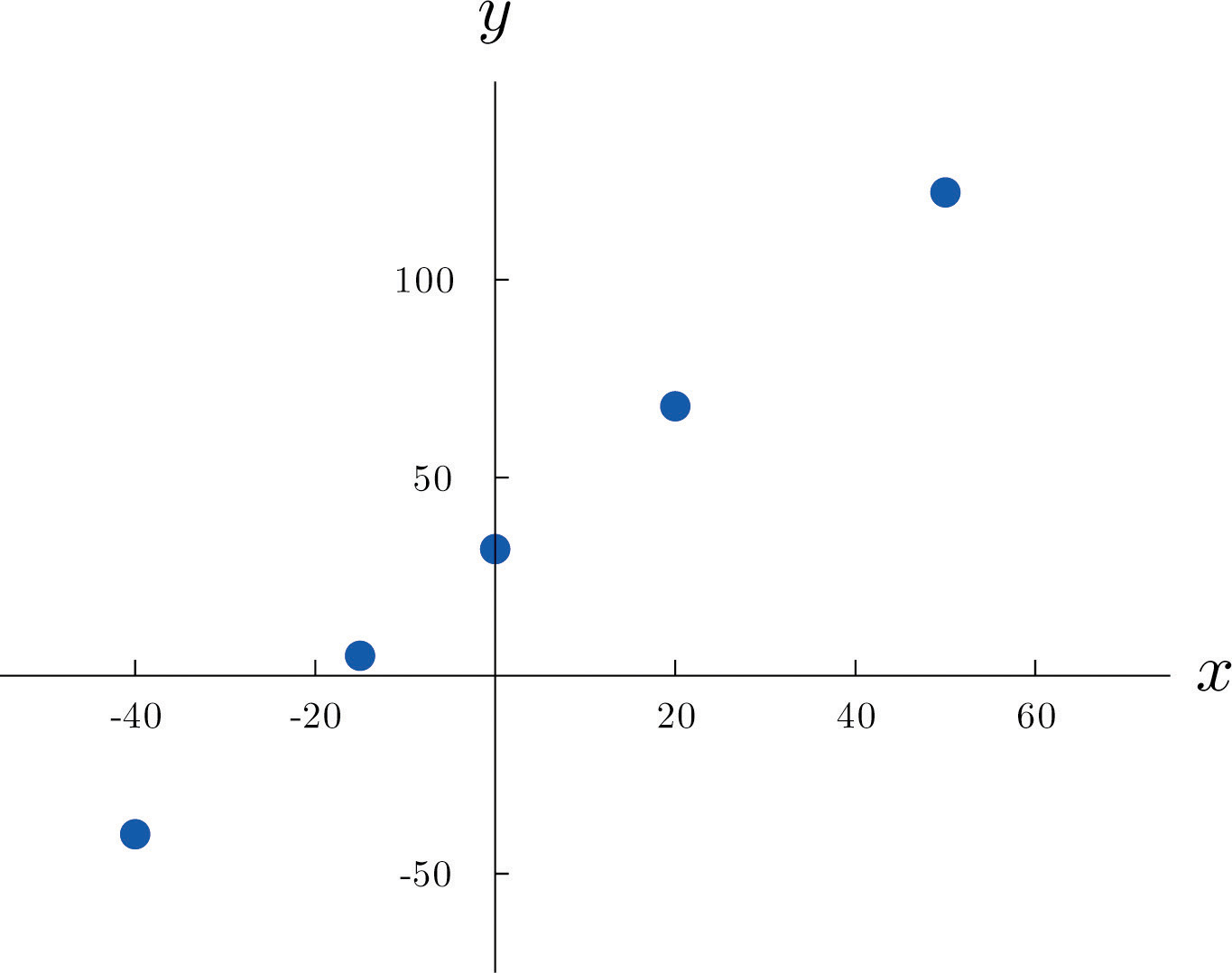
\[\begin{array}{c|c c c c c} x & -40 & -15 & 0 & 20 & 50 \\ \hline y &-40 &5 &32 &68 &122\\ \end{array}\]
Podemos trazar estos datos eligiendo un par de líneas perpendiculares en el plano, llamadas ejes de coordenadas, como se muestra en la Figura\(\PageIndex{1}\). Entonces a cada par de números en la tabla asociamos un punto único en el plano, el punto que se encuentra\(x\) unidades a la derecha del eje vertical (a la izquierda si\(x<0\)) e y unidades por encima del eje horizontal (debajo si\(y<0\)). La relación entre\(x\) y\(y\) se llama relación lineal porque los puntos así trazados se encuentran en una sola línea recta. El número\(95\) en la ecuación\(y=95x+32\) es la pendiente de la línea, y mide su inclinación. Describe cómo y cambia en respuesta a un cambio en\(x\): si\(x\) aumenta por\(1\) unidad entonces\(y\) aumenta (ya que\(95\) es positivo) por\(95\) unidad. Si la pendiente hubiera sido negativa entonces\(y\) habría disminuido en respuesta a un incremento de\(x\). El número\(32\) en la fórmula\(y=95x+32\) es la\(y\) -intercepción de la línea; identifica dónde la línea cruza el\(y\) eje -eje. Se puede recordar de un curso anterior que cada línea no vertical en el plano es descrita por una ecuación de la forma\(y=mx+b\), donde\(m\) está la pendiente de la línea y\(b\) es su\(y\) -intercepción.
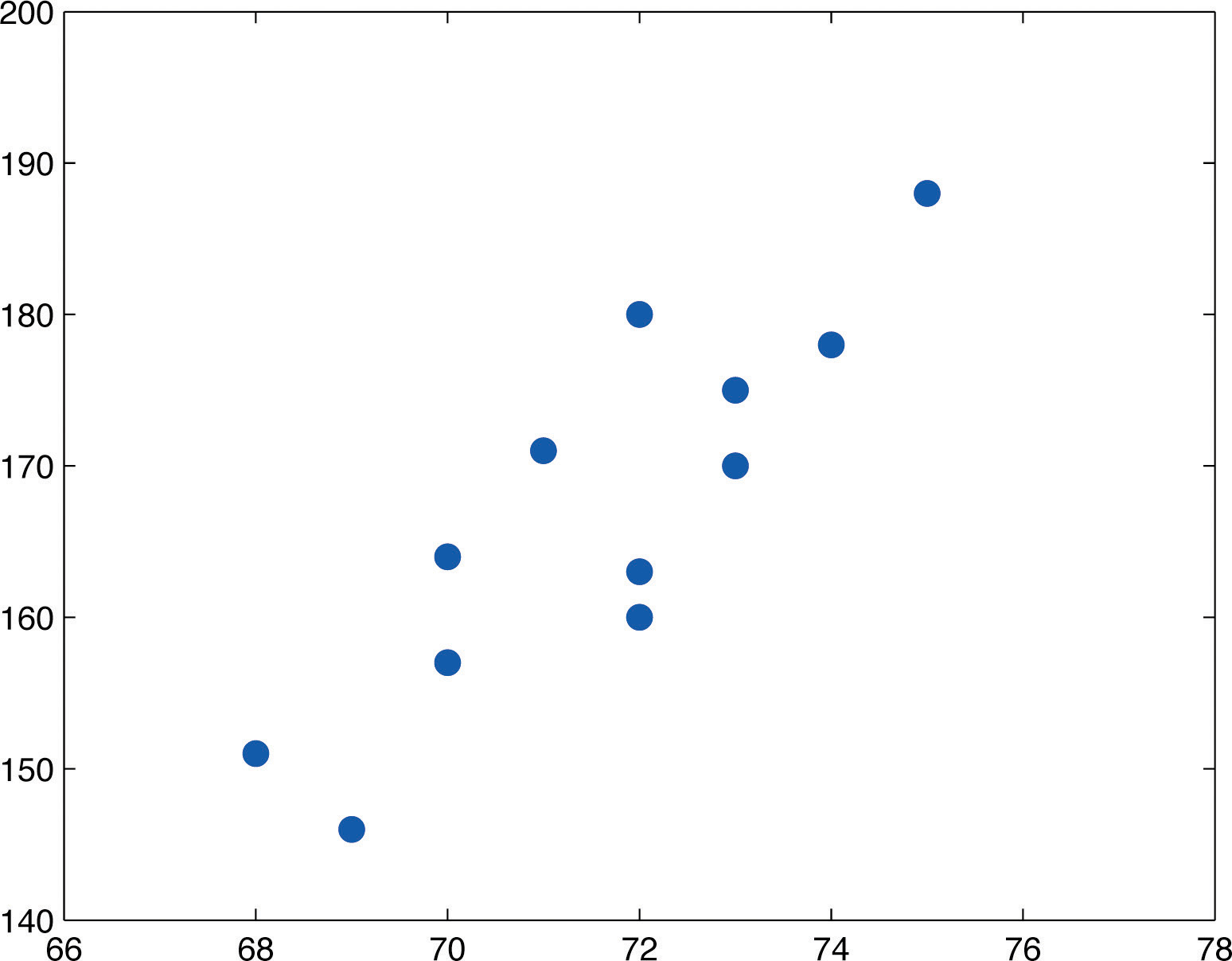
La relación entre\(x\) y\(y\) en el ejemplo de temperatura es determinista porque una vez que\(x\) se conoce el valor de,\(y\) se determina completamente el valor de. En contraste, todas las demás relaciones enumeradas en la tabla anterior tienen un elemento de aleatoriedad en ellas. Considera la relación descrita en la última línea de la tabla, la altura\(x\) de un hombre envejecido\(25\) y su peso\(y\). Si seleccionáramos aleatoriamente a hombres\(25\) de varios años y mediéramos la estatura y el peso de cada uno, podríamos obtener una colección de\((x,y)\) pares algo como esto:
\[(68,151)\; \; (72,163)\; \; (69,146)\; \; (72,180)\; \; (70,157)\; \; (73,170)\; \; (70,164)\; \; (73,175)\; \; (71,171)\; \; (74,178)\; \; (72,160)\; \; (75,188)\]
Una gráfica de estos datos se muestra en la Figura\(\PageIndex{2}\). Tal gráfica se llama diagrama de dispersión o diagrama de dispersión. Al mirar la trama es evidente que existe una relación lineal entre la altura\(x\) y el peso\(y\), pero no una perfecta. Los puntos parecen estar siguiendo una línea, pero no exactamente. Hay un elemento de aleatoriedad presente.
En este capítulo analizaremos situaciones en las que las variables\(x\) y\(y\) exhiben tal relación lineal con la aleatoriedad. El nivel de aleatoriedad variará de una situación a otra. En el ejemplo introductorio conectando una corriente eléctrica y el nivel de monóxido de carbono en el aire, la relación es casi perfecta. En otras situaciones, como la altura y los pesos de los individuos, la conexión entre las dos variables implica un alto grado de aleatoriedad. En la siguiente sección veremos cómo cuantificar la fuerza de la relación lineal entre dos variables.
Llave para llevar
- Dos variables\(x\) y\(y\) tienen una relación lineal determinista si los puntos trazados a partir de\((x,y)\) pares se encuentran exactamente a lo largo de una sola línea recta.
- En la práctica es común que dos variables exhiban una relación cercana a lineal pero que contiene un elemento, posiblemente grande, de aleatoriedad.