10.2: El coeficiente de correlación lineal
- Page ID
- 151180
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
Aprender qué es el coeficiente de correlación lineal, cómo calcularlo y qué nos dice sobre la relación entre dos variables\(x\) y\(y\)
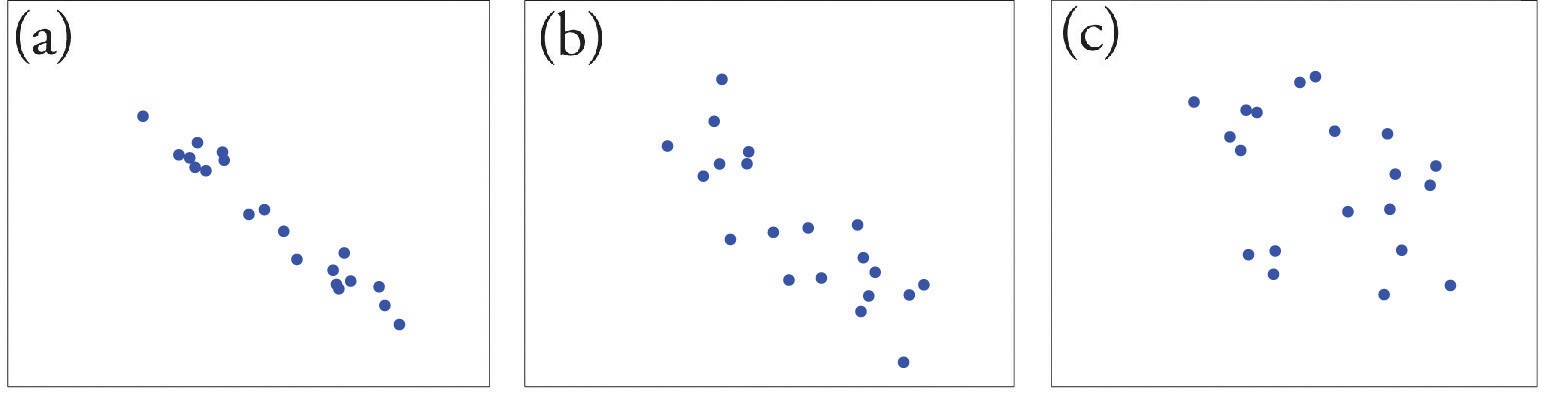
La figura\(\PageIndex{1}\) ilustra las relaciones lineales entre dos variables\(x\) y\(y\) de intensidades variables. Es visualmente evidente que en la situación en el panel (a),\(x\) podría servir como predictor útil de\(y\), sería menos útil en la situación ilustrada en el panel (b), y en la situación del panel (c) la relación lineal es tan débil como para ser prácticamente inexistente. El coeficiente de correlación lineal es un número calculado directamente a partir de los datos que mide la fuerza de la relación lineal entre las dos variables\(x\) y\(y\).
Definición: coeficiente de correlación lineal
El coeficiente de correlación lineal para una colección de\(n\) pares\(x\) de números en una muestra es el número\(r\) dado por la fórmula
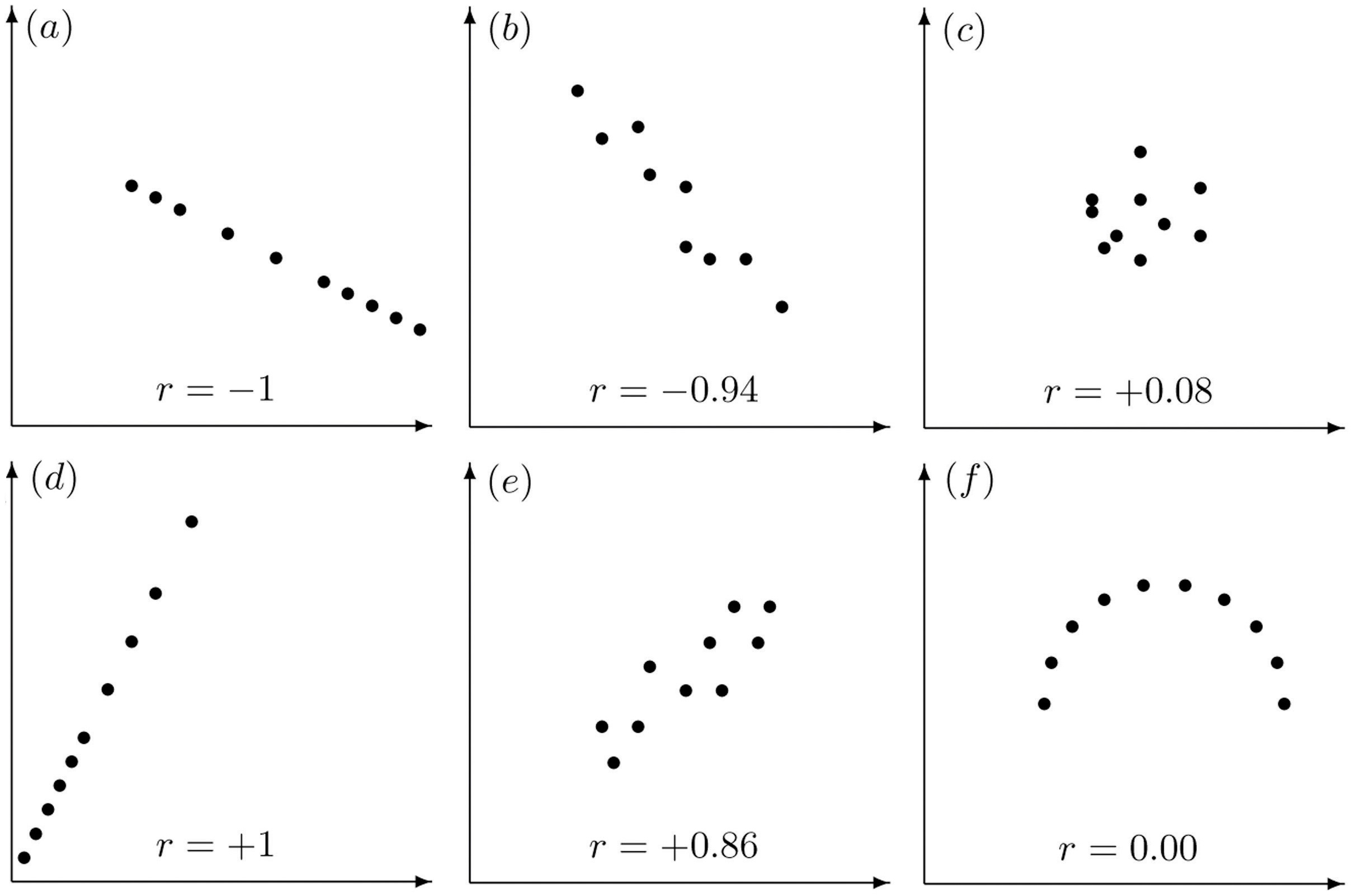
El coeficiente de correlación lineal tiene las siguientes propiedades, ilustradas en la Figura\(\PageIndex{2}\)
- El valor de las\(r\) mentiras entre\(−1\) y\(1\), inclusivo.
- El signo de\(r\) indica la dirección de la relación lineal entre\(x\) y\(y\):
- El tamaño de\(|r|\) indica la fuerza de la relación lineal entre\(x\) y\(y\):
- Si\(|r|\) está cerca\(1\) (es decir, si\(r\) está cerca de cualquiera\(1\) o\(−1\)), entonces la relación lineal entre\(x\) y\(y\) es fuerte.
- Si\(|r|\) está cerca\(0\) (es decir, si\(r\) está cerca\(0\) y de cualquier signo). entonces la relación lineal entre\(x\) y\(y\) es débil.
para que
\[ r= \dfrac{SS_{xy}}{\sqrt{SS_{xx}SS_{yy}}}=\dfrac{2.44.583}{\sqrt{(46.916)(1690.916)}}=0.868\]
El número cuantifica lo que es visualmente aparente a partir de\(\PageIndex{2}\) los pesos de las figuras tiende a aumentar linealmente con la altura (\(r\)es positivo) y aunque la relación no es perfecta, es razonablemente fuerte (\(r\)está cerca\(1\)).
Ejemplo\(\PageIndex{1}\)
Calcular el coeficiente de correlación lineal para los pares altura y peso trazados en la Figura\(\PageIndex{2}\).
Solución:
Incluso para conjuntos de datos pequeños como este, los cálculos son demasiado largos para hacerlos completamente a mano. En la práctica real los datos se ingresan en una calculadora o computadora y se utiliza un programa de estadísticas. Para aclarar el significado de las fórmulas mostraremos los datos y las cantidades relacionadas en forma tabular. Para cada
| \(x\) | \(y\) | \(x^2\) | \(y^2\) | |
|---|---|---|---|---|
| 68 | \ (x\) ">151 | \ (y\) ">4624 | \ (x^2\) ">10268 | \ (y^2\) ">22801 |
| 69 | \ (x\) ">146 | \ (y\) ">4761 | \ (x^2\) ">10074 | \ (y^2\) ">21316 |
| 70 | \ (x\) ">157 | \ (y\) ">4900 | \ (x^2\) ">10990 | \ (y^2\) ">24649 |
| 70 | \ (x\) ">164 | \ (y\) ">4900 | \ (x^2\) ">11480 | \ (y^2\) ">26896 |
| 71 | \ (x\) ">171 | \ (y\) ">5041 | \ (x^2\) ">12141 | \ (y^2\) ">29241 |
| 72 | \ (x\) ">160 | \ (y\) ">5184 | \ (x^2\) ">11520 | \ (y^2\) ">25600 |
| 72 | \ (x\) ">163 | \ (y\) ">5184 | \ (x^2\) ">11736 | \ (y^2\) ">26569 |
| 72 | \ (x\) ">180 | \ (y\) ">5184 | \ (x^2\) ">12960 | \ (y^2\) ">32400 |
| 73 | \ (x\) ">170 | \ (y\) ">5329 | \ (x^2\) ">12410 | \ (y^2\) ">28900 |
| 73 | \ (x\) ">175 | \ (y\) ">5329 | \ (x^2\) ">12775 | \ (y^2\) ">30625 |
| 74 | \ (x\) ">178 | \ (y\) ">5476 | \ (x^2\) ">13172 | \ (y^2\) ">31684 |
| 75 | \ (x\) ">188 | \ (y\) ">5625 | \ (x^2\) ">14100 | \ (y^2\) ">35344 |
| 859 | \ (x\) ">2003 | \ (y\) ">61537 | \ (x^2\) ">143626 | \ (y^2\) ">336025 |
Llave para llevar
- El coeficiente de correlación lineal mide la fuerza y dirección de la relación lineal entre dos variables\(x\) y\(y\).
- El signo del coeficiente de correlación lineal indica la dirección de la relación lineal entre\(x\) y\(y\).
- Cuando\(r\) está cerca\(1\) o\(−1\) la relación lineal es fuerte; cuando está cerca\(0\) la relación lineal es débil.