10.3: Modelado de Relaciones Lineales con Aleatoriedad Presente

Última actualización
Guardar como PDF

Page ID: 151178

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Conocer el marco en el que se\(y\) realizará el análisis estadístico de la relación lineal entre dos variables\(x\) y

En este capítulo se trata de una población para la que podemos asociar a cada elemento dos medidas,\(x\) y\(y\). Nos interesan situaciones en las que el valor de\(x\) pueda ser utilizado para sacar conclusiones sobre el valor de\(y\), como predecir el valor de reventa\(y\) de una casa residencial en función de su tamaño\(x\). Dado que la relación entre\(x\) y no\(y\) es determinista, se deben aplicar procedimientos estadísticos. Para cualquier procedimiento estadístico, dado en este libro o en otro lugar, las fórmulas asociadas son válidas sólo bajo supuestos específicos. El conjunto de supuestos en regresión lineal simple son una descripción matemática de la relación entre\(x\) y\(y\). Tal conjunto de suposiciones se conoce como modelo.

Por cada valor fijo de\(x\), se determina una subpoblación de la población completa, como la colección de todas las casas con pies\(2,100\) cuadrados de espacio habitable. Para cada elemento de esa subpoblación hay una medida\(y\), como el valor de cualquier casa de\(2,100\) -pies cuadrados. Dejar\(E(y)\) denotar la media de todos los\(y\) -valores para cada valor particular de\(x\). \(E(y)\)puede cambiar de\(x\) -valor a\(x\) -valor, como el valor medio de todas las casas de\(2,100\) -pies cuadrados, el valor medio (diferente) para todas las casas de pies\(2,500\) cuadrados, y así sucesivamente.

Nuestra primera suposición es que la relación entre\(x\) y la media de los\(y\) -valores en la subpoblación determinada por\(x\) es lineal. Esto quiere decir que existen números tales que

\[ y = \beta_1 x+\beta_0 \]

Esta relación lineal es la razón de la palabra “lineal” en “regresión lineal simple” a continuación. (La palabra “simple” significa que\(y\) depende sólo de otra variable y no de dos o más.)

Nuestra siguiente suposición es que para cada valor de\(x\) los\(y\) -valores se dispersan alrededor de la media de\(E(y)\) acuerdo con una distribución normal centrada en\(E(y)\) y con una desviación estándar\(σ\) que es la misma para cada valor de\(x\). Esto es lo mismo que decir que existe una variable aleatoria normalmente distribuida\(ε\) con media\(0\) y desviación estándar\(σ\) para que la relación entre\(x\) y\(y\) en toda la población sea

\[ y = \beta_1 x+\beta_0 + \epsilon \]

Nuestra última suposición es que las desviaciones aleatorias asociadas a diferentes observaciones son independientes.

En resumen, el modelo es:

Modelo de regresión lineal simple

Para cada punto\((x,y)\) del conjunto de datos, el\(y\) valor -valor es una observación independiente de

\[y=β_1x+β_0+ε\]

donde\(β_1\) y\(β_0\) son parámetros fijos y\(ε\) es una variable aleatoria normalmente distribuida con media\(0\) y una desviación estándar desconocida\(σ\).

La línea con ecuación

\[y=β_1x + β_0\]

se llama la línea de regresión poblacional.

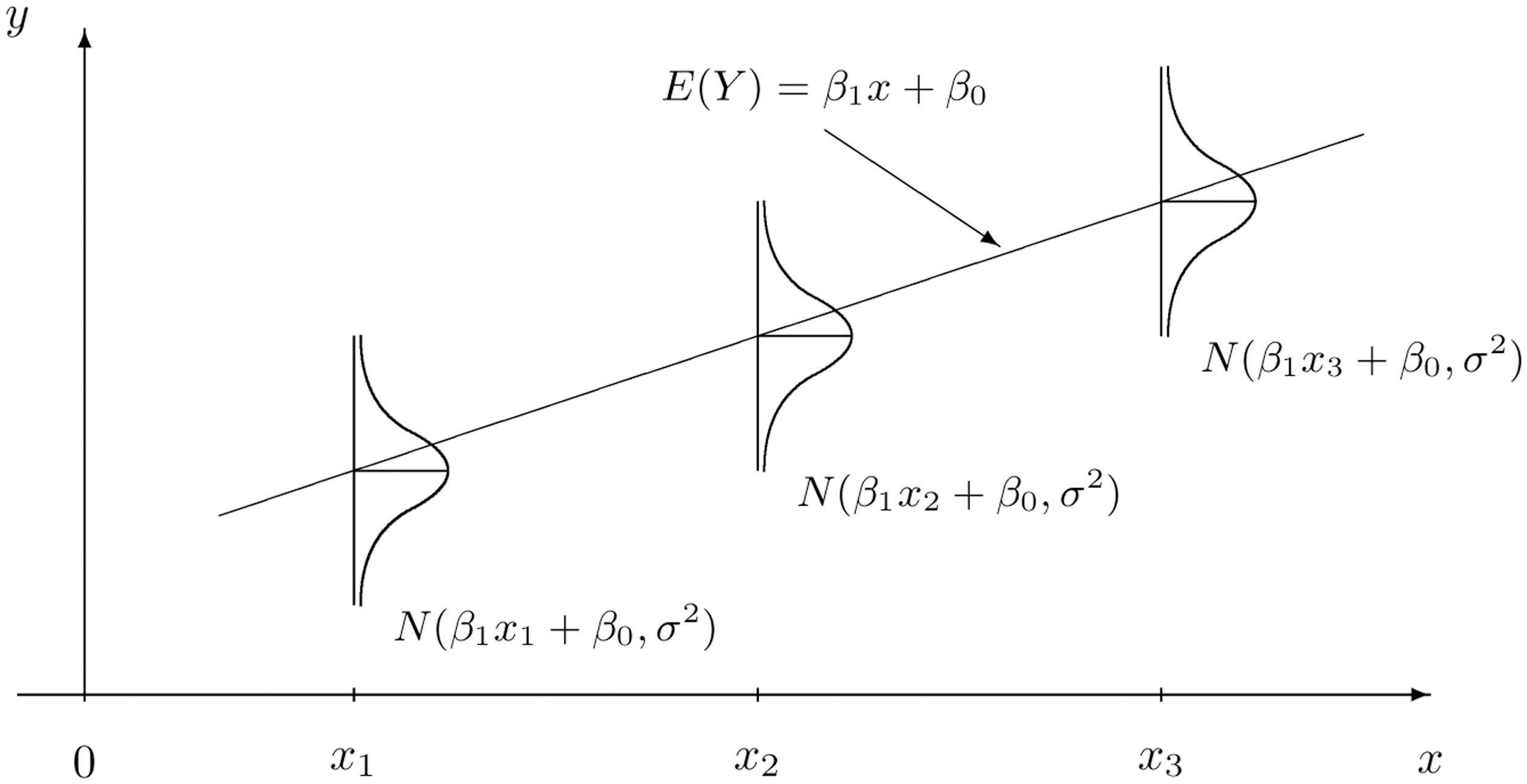
Figura\(\PageIndex{1}\): El concepto de modelo lineal simple

Es conceptualmente importante ver el modelo como una suma de dos partes:

\[ y = \underbrace{ \beta_1 x+\beta_0}_{\text{Deterministic}} + \underbrace{\epsilon}_{\text{Random}}\]

Parte Determinística. La primera parte\(0\) es la ecuación que describe la tendencia en\(y\) como\(x\) incrementos. La línea que parece que vemos cuando miramos el diagrama de dispersión es una aproximación de la línea No\[ y = \beta_1 x+\beta_0.\] hay nada aleatorio en esta parte, y por lo tanto se llama la parte determinista del modelo.
Parte Aleatoria. La segunda parte\(ε\) es una variable aleatoria, a menudo llamada término de error o ruido. Esta parte explica por qué los valores reales observados de no\(y\) están exactamente encendidos sino que fluctúan cerca de una línea. La información sobre este término es importante ya que sólo cuando se sabe cuánto ruido hay en los datos se puede saber cuán confiable es la tendencia detectada.

Existen procedimientos para verificar la validez de los tres supuestos, pero para nosotros bastará con verificar visualmente la tendencia lineal en los datos. Si el conjunto de datos es grande entonces los puntos en el diagrama de dispersión formarán una banda alrededor de una línea recta aparente. La normalidad de\(ε\) con una desviación estándar constante corresponde gráficamente a que la banda sea de ancho aproximadamente constante, y con la mayoría de los puntos concentrados cerca de la mitad de la banda.

Afortunadamente, los tres supuestos no necesitan sostenerse exactamente para que los procedimientos y análisis desarrollados en este capítulo sean útiles.

Llave para llevar

Los procedimientos estadísticos sólo son válidos cuando ciertos supuestos son válidos. Los supuestos que subyacen a los análisis realizados en este capítulo se resumen gráficamente en la Figura\(\PageIndex{1}\).