11.1: Pruebas de Chi-cuadrado para la independencia
- Page ID
- 151160
Objetivos de aprendizaje
- Entender qué son las distribuciones de chi-cuadrado.
- Entender cómo utilizar una prueba de chi-cuadrado para juzgar si dos factores son independientes.
Distribuciones Chi-Cuadradas
Como saben, existe toda una familia de\(t\) -distribuciones, cada una especificada por un parámetro llamado los grados de libertad, denotado\(df\). De igual manera, todas las distribuciones chi-cuadrado forman una familia, y cada uno de sus miembros también se especifica por un parámetro\(df\), el número de grados de libertad. Chi es una letra griega denotada por el símbolo\(\chi\) y chi-cuadrado a menudo se denota por\(\chi^2\).
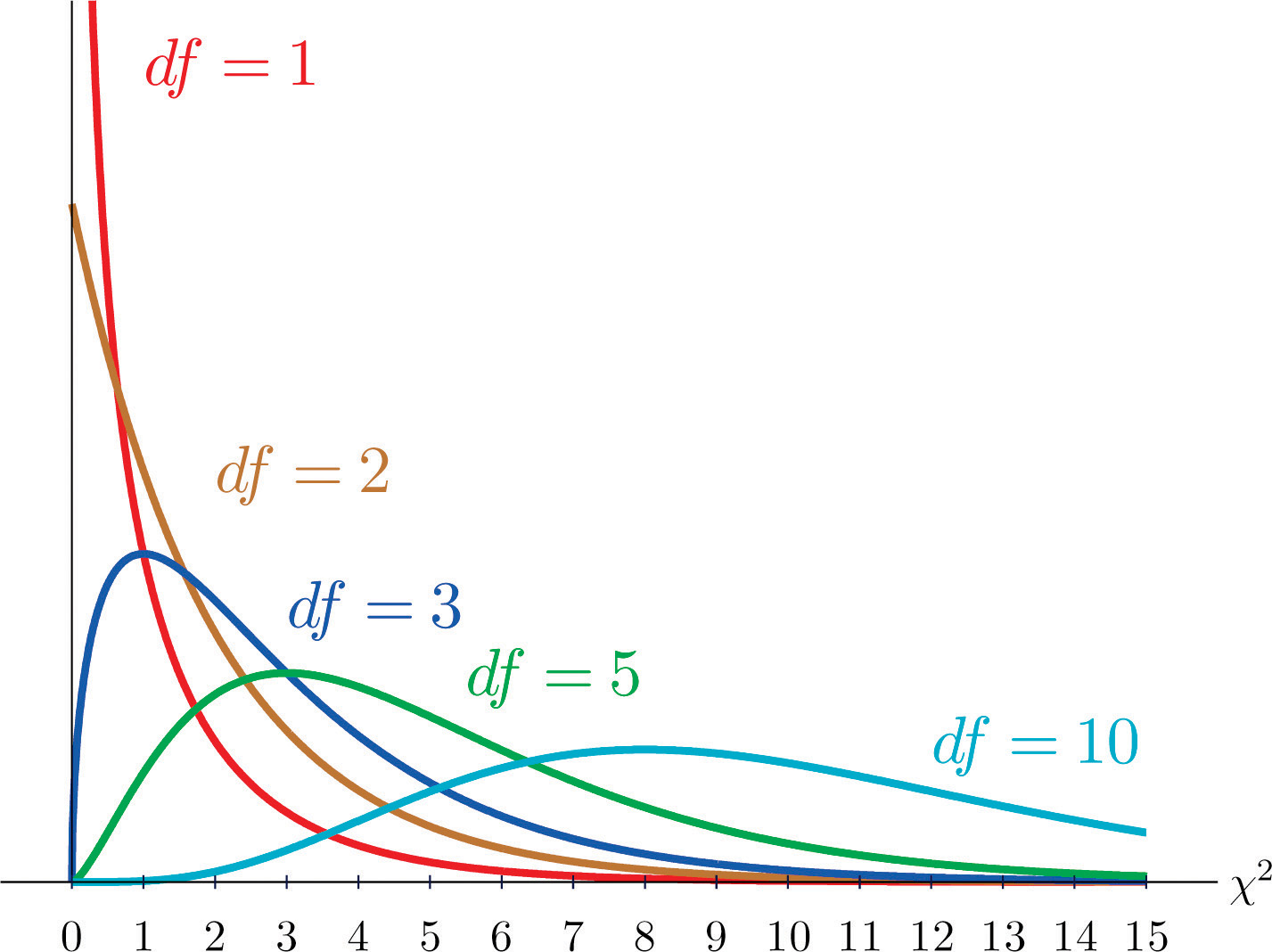
La figura\(\PageIndex{1}\) muestra varias distribuciones\(\chi\) -cuadradas para diferentes grados de libertad. Una variable aleatoria chi-cuadrada es una variable aleatoria que asume solo valores positivos y sigue una distribución\(\chi\) -cuadrada.
Definición: valor crítico
El valor de la variable aleatoria chi-cuadrada\(\chi^2\) con\(df=k\) que corta una cola derecha de área\(c\) se denota\(\chi_c^2\) y se denomina valor crítico (Figura\(\PageIndex{2}\)).
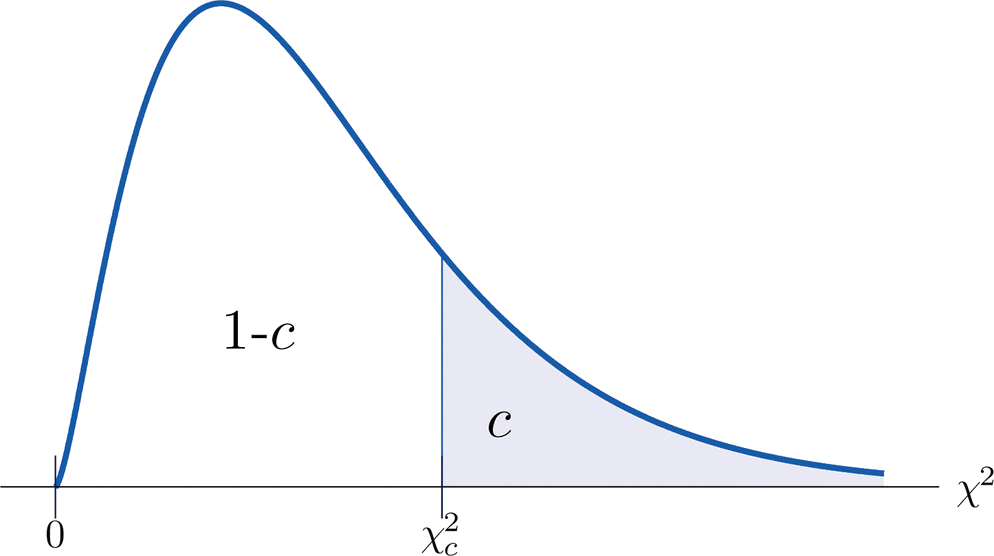
La\(\PageIndex{3}\) siguiente figura da valores de\(\chi_c^2\) para diversos valores de\(c\) y bajo varias distribuciones de chi-cuadrado con diversos grados de libertad.

Pruebas para la Independencia
Las pruebas de hipótesis encontradas anteriormente en el libro tuvieron que ver con cómo se compararon los valores numéricos de dos parámetros poblacionales. En esta subsección investigaremos hipótesis que tienen que ver con si dos variables aleatorias toman o no sus valores de manera independiente, o si el valor de una tiene relación con el valor de la otra. Así las hipótesis se expresarán en palabras, no en símbolos matemáticos. Construimos la discusión en torno al siguiente ejemplo.
Existe la teoría de que el género de un bebé en el útero está relacionado con la frecuencia cardíaca del bebé: las niñas tienden a tener frecuencias cardíacas más altas. Supongamos que deseamos probar esta teoría. Examinamos los registros de frecuencia cardíaca de\(40\) los bebés tomados durante los últimos chequeos prenatales de sus madres antes del parto, y a cada uno de estos registros seleccionados\(40\) aleatoriamente calculamos los valores de dos medidas aleatorias: 1) género y 2) frecuencia cardíaca. En este contexto estas dos medidas aleatorias suelen denominarse factores. Dado que la carga de la prueba es que la frecuencia cardíaca y el género están relacionados, no que no estén relacionados, el problema de probar la teoría sobre el género del bebé y la frecuencia cardíaca puede formularse como una prueba de las siguientes hipótesis:
\[H_0: \text{Baby gender and baby heart rate are independent}\\ vs. \\ H_a: \text{Baby gender and baby heart rate are not independent}\]
El factor género tiene dos categorías o niveles naturales: niño y niña. Dividimos el segundo factor, la frecuencia cardíaca, en dos niveles, bajo y alto, eligiendo alguna frecuencia cardíaca, digamos\(145\) latidos por minuto, como el corte entre ellos. Una frecuencia cardíaca por debajo de los\(145\) latidos por minuto se considerará baja\(145\) y por encima considerada alta. Los\(40\) registros dan lugar a una tabla\(2\times 2\) de contingencia. Al unir los totales de fila, los totales de columna y un total general obtenemos la tabla que se muestra como Tabla\(\PageIndex{1}\). Las cuatro entradas en negritas son recuentos de observaciones de la muestra de\(n = 40\). Había\(11\) niñas con frecuencia cardíaca baja,\(17\) chicos con frecuencia cardíaca baja, y así sucesivamente. Forman el núcleo de la mesa ampliada.
| Ritmo Cardíaco | ||||
|---|---|---|---|---|
| \(\text{Low}\) | \(\text{High}\) | \(\text{Row Total}\) | ||
| \(\text{Gender}\) | \(\text{Girl}\) | \ (\ text {Bajo}\)” style="vertical-align:middle; ">\(11\) | \ (\ text {Alto}\)” style="vertical-align:middle; ">\(7\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(18\) |
| \(\text{Boy}\) | \ (\ text {Bajo}\)” style="vertical-align:middle; ">\(17\) | \ (\ text {Alto}\)” style="vertical-align:middle; ">\(5\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(22\) | |
| \(\text{Column Total}\) | \ (\ text {Bajo}\)” style="vertical-align:middle; ">\(28\) | \ (\ text {Alto}\)” style="vertical-align:middle; ">\(12\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(\text{Total}=40\) | |
En analogía con el hecho de que la probabilidad de eventos independientes es producto de las probabilidades de cada evento, si la frecuencia cardíaca y el género fueran independientes entonces esperaríamos que el número en cada celda central estuviera cerca del producto del total de fila\(R\) y el total de columna\(C\) de la fila y columna que la contiene, dividida por el tamaño de la muestra\(n\). Denotando tal número esperado de observaciones\(E\), estos cuatro valores esperados son:
- 1ª fila y 1ª columna:\(E=(R\times C)/n = 18\times 28 /40 = 12.6\)
- 1ª fila y 2ª columna:\(E=(R\times C)/n = 18\times 12 /40 = 5.4\)
- 2ª fila y 1ª columna:\(E=(R\times C)/n = 22\times 28 /40 = 15.4\)
- 2ª fila y 2ª columna:\(E=(R\times C)/n = 22\times 12 /40 = 6.6\)
Actualizamos Table\(\PageIndex{1}\) colocando cada valor esperado en su celda central correspondiente, justo debajo del valor observado en la celda. Esto da la tabla actualizada Tabla\(\PageIndex{2}\).
| \(\text{Heart Rate}\) | ||||
|---|---|---|---|---|
| \(\text{Low}\) | \(\text{High}\) | \(\text{Row Total}\) | ||
| \(\text{Gender}\) | \(\text{Girl}\) | \ (\ text {Frecuencia Cardíaca}\)\(\text{Low}\) "style="vertical-align:middle;" >
\(O=11\) \(E=12.6\) |
\ (\ text {Frecuencia Cardíaca}\)\(\text{High}\) "style="vertical-align:middle;" >
\(O=7\) \(E=5.4\) |
\ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(R = 18\) |
| \(\text{Boy}\) | \ (\ text {Frecuencia Cardíaca}\)\(\text{Low}\) "style="vertical-align:middle;" >
\(O=17\) \(E=15.4\) |
\ (\ text {Frecuencia Cardíaca}\)\(\text{High}\) "style="vertical-align:middle;" >
\(O=5\) \(E=6.6\) |
\ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(R = 22\) | |
| \(\text{Column Total}\) | \ (\ text {Frecuencia Cardíaca}\)\(\text{Low}\) "style="vertical-align:middle;" >\(C = 28\) | \ (\ text {Frecuencia Cardíaca}\)\(\text{High}\) "style="vertical-align:middle;" >\(C = 12\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(n = 40\) | |
Una medida de cuánto se desvían los datos de lo que esperaríamos ver si los factores realmente fueran independientes es la suma de los cuadrados de la diferencia de los números en cada celda central, o, estandarizando dividiendo cada cuadrado por el número esperado en la celda, la suma\(\sum (O-E)^2 / E\). Rechazaríamos la hipótesis nula de que los factores son independientes solo si este número es grande, por lo que la prueba es de cola derecha. En este ejemplo la variable aleatoria\(\sum (O-E)^2 / E\) tiene la distribución chi-cuadrada con un grado de libertad. Si hubiéramos decidido desde el principio probar en el\(10\%\) nivel de significancia, el valor crítico que define la región de rechazo sería, leyendo de la Figura\(\PageIndex{3}\),\(\chi _{\alpha }^{2}=\chi _{0.10 }^{2}=2.706\), de manera que la región de rechazo sería el intervalo\([2.706,\infty )\). Cuando calculamos el valor del estadístico de prueba estandarizado obtenemos
\[\sum \frac{(O-E)^2}{E}=\frac{(11-12.6)^2}{12.6}+\frac{(7-5.4)^2}{5.4}+\frac{(17-15.4)^2}{15.4}+\frac{(5-6.6)^2}{6.6}=1.231\]
Ya que\(1.231 < 2.706\), la decisión no es rechazar\(H_0\). Ver Figura\(\PageIndex{4}\). Los datos no aportan evidencia suficiente, a\(10\%\) nivel de significancia, para concluir que la frecuencia cardíaca y el género están relacionados.
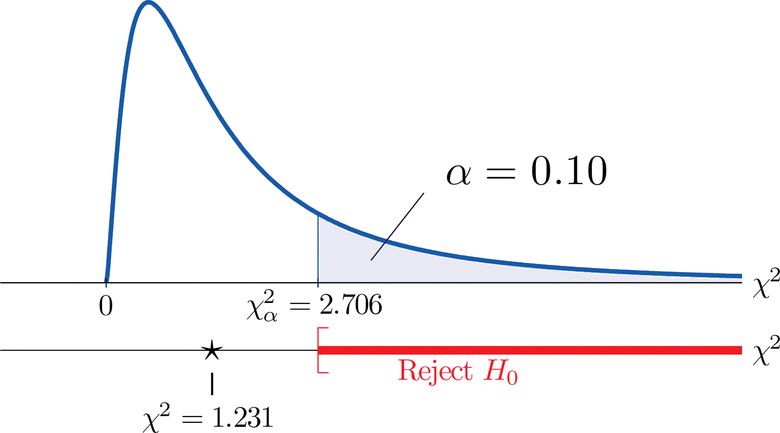
Higo ure\(\PageIndex{4}\): Predicción del género del bebé
H 0 vs. H a : : El género del bebé y la frecuencia cardíaca del bebé son independiente Género del bebé y la frecuencia cardíaca del bebé son n o t independientes H 0 vs. H a : : El género del bebé y la frecuencia cardíaca del bebé son Género del bebé independiente y la frecuencia cardíaca del bebé son n o t independientes
Con este ejemplo específico en mente, ahora volvamos a la situación general. En el marco general de probar la independencia de dos factores, llamarlos Factor\(1\) y Factor\(2\), las hipótesis a probar son
\[H_0: \text{The two factors are independent}\\ vs. \\ H_a: \text{The two factors are not independent}\]
Al igual que en el ejemplo cada factor se divide en una serie de categorías o niveles. Estos podrían surgir de forma natural, como en la división de género chico-niña, o algo arbitrariamente, como en la división alta-baja de la frecuencia cardíaca. Supongamos que Factor\(1\) tiene\(I\) niveles y Factor\(2\) tiene\(J\) niveles. Entonces la información de una muestra aleatoria da lugar a una tabla de\(I\times J\) contingencia general, que con totales de fila, totales de columna y un total general aparecería como se muestra en Tabla\(\PageIndex{3}\). Cada celda puede estar etiquetada por un par de índices\((i,j)\). \(O_{ij}\)representa el recuento observado de observaciones en la celda en fila\(i\) y columna\(j\),\(R_i\) para el total de\(i^{th}\) fila y\(C_j\) para el total de\(j^{th}\) columna. Para simplificar la notación bajaremos los índices así Tabla\(\PageIndex{3}\) se convierte en Tabla\(\PageIndex{4}\). Sin embargo, es importante tener en cuenta que el\(Os\), el\(Rs\) y el\(Cs\), aunque denotados por los mismos símbolos, son en realidad números diferentes.
| \(\text{Factor 2 Levels}\) | |||||||
|---|---|---|---|---|---|---|---|
| \(1\) | ⋅ ⋅ | \(j\) | ⋅ ⋅ | \(J\) | \(\text{Row Total}\) | ||
| \(\text{Factor 1 Levels}\) | \(1\) | \ (\ text {Factor 2 Niveles}\)\(1\) "style="vertical-align:middle;" >\(O_{11}\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" > ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(j\) "style="vertical-align:middle;" >\(O_{1j}\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" > ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(J\) "style="vertical-align:middle;" >\(O_{1J}\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(R_1\) |
| ́n | \ (\ text {Factor 2 Niveles}\)\(1\) "style="vertical-align:middle;" > | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" >azcapotzalco | \ (\ text {Factor 2 Niveles}\)\(j\) "style="vertical-align:middle;" > | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" >azcapotzalco | \ (\ text {Factor 2 Niveles}\)\(J\) "style="vertical-align:middle;" > | \ (\ text {Total de fila}\)” style="vertical-align:middle; "> | |
| \(i\) | \ (\ text {Factor 2 Niveles}\)\(1\) "style="vertical-align:middle;" >\(O_{i1}\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" > ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(j\) "style="vertical-align:middle;" >\(O_{ij}\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" > ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(J\) "style="vertical-align:middle;" >\(O_{iJ}\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(R_i\) | |
| ́n | \ (\ text {Factor 2 Niveles}\)\(1\) "style="vertical-align:middle;" > | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" >azcapotzalco | \ (\ text {Factor 2 Niveles}\)\(j\) "style="vertical-align:middle;" > | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" >azcapotzalco | \ (\ text {Factor 2 Niveles}\)\(J\) "style="vertical-align:middle;" > | \ (\ text {Total de fila}\)” style="vertical-align:middle; "> | |
| \(I\) | \ (\ text {Factor 2 Niveles}\)\(1\) "style="vertical-align:middle;" >\(O_{I1}\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" > ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(j\) "style="vertical-align:middle;" >\(O_{Ij}\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" > ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(J\) "style="vertical-align:middle;" >\(O_{IJ}\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(R_I\) | |
| \(\text{Column Total}\) | \ (\ text {Factor 2 Niveles}\)\(1\) "style="vertical-align:middle;" >\(C_1\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" > ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(j\) "style="vertical-align:middle;" >\(C_j\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ "style="vertical-align:middle;" > ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(J\) "style="vertical-align:middle;" >\(C_J\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(n\) | |
| \(\text{Factor 2 Levels}\) | |||||||
|---|---|---|---|---|---|---|---|
| \(1\) | ⋅ ⋅ | \(j\) | ⋅ ⋅ | \(J\) | \(\text{Row Total}\) | ||
|
\(\text{Factor 1 Levels}\) |
\(1\) | \ (\ text {Factor 2 Niveles}\)\(1\) “>\(O\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(j\) “>\(O\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(J\) “>\(O\) | \ (\ text {Total de fila}\) ">\(R\) |
| ́n | \ (\ text {Factor 2 Niveles}\)\(1\) “> | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>+' | \ (\ text {Factor 2 Niveles}\)\(j\) “> | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>+' | \ (\ text {Factor 2 Niveles}\)\(J\) “> | \ (\ text {Total de fila}\) "> | |
| \(i\) | \ (\ text {Factor 2 Niveles}\)\(1\) “>\(O\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(j\) “>\(O\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(J\) “>\(O\) | \ (\ text {Total de fila}\) ">\(R\) | |
| ́n | \ (\ text {Factor 2 Niveles}\)\(1\) “> | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>+' | \ (\ text {Factor 2 Niveles}\)\(j\) “> | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>+' | \ (\ text {Factor 2 Niveles}\)\(J\) “> | \ (\ text {Total de fila}\) "> | |
| \(I\) | \ (\ text {Factor 2 Niveles}\)\(1\) “>\(O\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(j\) “>\(O\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(J\) “>\(O\) | \ (\ text {Total de fila}\) ">\(R\) | |
| \(\text{Column Total}\) | \ (\ text {Factor 2 Niveles}\)\(1\) “>\(C\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(j\) “>\(C\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(J\) “>\(C\) | \ (\ text {Total de fila}\) ">\(n\) | |
Al igual que en el ejemplo, para cada celda central de la tabla calculamos cuál sería el número esperado\(E\) de observaciones si los dos factores fueran independientes. \(E\)se calcula para cada celda central (cada celda con una\(O\) en ella) de Table\(\PageIndex{4}\) por la regla aplicada en el ejemplo:
\[E=R×Cn\]
donde\(R\) es el total de fila y\(C\) es el total de la columna correspondiente a la celda, y\(n\) es el tamaño de la muestra
| \(\text{Factor 2 Levels}\) | |||||||
|---|---|---|---|---|---|---|---|
| \(1\) | ⋅ ⋅ | \(j\) | ⋅ ⋅ | \(J\) | \(\text{Row Total}\) | ||
|
\(\text{Factor 1 Levels}\) |
\(1\) | \ (\ text {Factor 2 Niveles}\)\(1\) “>
\(O\) \(E\) |
\ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>
⋅ ⋅ |
\ (\ text {Factor 2 Niveles}\)\(j\) “>
\(O\) \(E\) |
\ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>
⋅ ⋅ |
\ (\ text {Factor 2 Niveles}\)\(J\) “>
\(O\) \(E\) |
\ (\ text {Total de fila}\) ">
\(R\) |
| ́n | \ (\ text {Factor 2 Niveles}\)\(1\) “> | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>+' | \ (\ text {Factor 2 Niveles}\)\(j\) “> | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>+' | \ (\ text {Factor 2 Niveles}\)\(J\) “> | \ (\ text {Total de fila}\) "> | |
| \(i\) | \ (\ text {Factor 2 Niveles}\)\(1\) “>
\(O\) \(E\) |
\ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>
⋅ ⋅ |
\ (\ text {Factor 2 Niveles}\)\(j\) “>
\(O\) \(E\) |
\ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>
⋅ ⋅ |
\ (\ text {Factor 2 Niveles}\)\(J\) “>
\(O\) \(E\) |
\ (\ text {Total de fila}\) ">
\(R\) |
|
| ́n | \ (\ text {Factor 2 Niveles}\)\(1\) “> | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>+' | \ (\ text {Factor 2 Niveles}\)\(j\) “> | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>+' | \ (\ text {Factor 2 Niveles}\)\(J\) “> | \ (\ text {Total de fila}\) "> | |
| \(I\) | \ (\ text {Factor 2 Niveles}\)\(1\) “>
\(O\) \(E\) |
\ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>
⋅ ⋅ |
\ (\ text {Factor 2 Niveles}\)\(j\) “>
\(O\) \(E\) |
\ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “>
⋅ ⋅ |
\ (\ text {Factor 2 Niveles}\)\(J\) “>
\(O\) \(E\) |
\ (\ text {Total de fila}\) ">
\(R\) |
|
| \(\text{Column Total}\) | \ (\ text {Factor 2 Niveles}\)\(1\) “>\(C\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(j\) “>\(C\) | \ (\ text {Factor 2 Niveles}\) ⋅ ⋅ ⋅ “> ⋅ ⋅ ⋅ | \ (\ text {Factor 2 Niveles}\)\(J\) “>\(C\) | \ (\ text {Total de fila}\) ">\(n\) | |
Aquí está el estadístico de prueba para la hipótesis general basada en Tabla\(\PageIndex{5}\), junto con las condiciones de que sigue una distribución chi-cuadrada.
Estadística de prueba para probar la independencia de dos factores
\[\chi^2=\sum (O−E)^2E\]
donde la suma está sobre todas las celdas centrales de la tabla.
Si
- los dos factores de estudio son independientes, y
- el recuento observado\(O\) de cada celda en la Tabla\(\PageIndex{5}\) es al menos\(5\),
luego\(\chi ^2\) aproximadamente sigue una distribución chi-cuadrada con\(df=(I-1)\times (J-1)\) grados de libertad.
Se utilizan los mismos procedimientos de cinco pasos, ya sea el enfoque de\(p\) valor crítico o el enfoque -valor, que se introdujeron en la Sección 8.1 y Sección 8.3 para realizar la prueba, que siempre es de cola derecha.
Ejemplo\(\PageIndex{1}\)
Un investigador desea investigar si los puntajes de los estudiantes en un examen de ingreso a la universidad (\(CEE\)) tienen algún poder indicativo para el desempeño universitario futuro medido por\(GPA\). Es decir, desea investigar si los factores\(CEE\) y\(GPA\) son independientes o no. Selecciona aleatoriamente a\(n = 100\) estudiantes en una universidad y anota la puntuación de cada estudiante en el examen de ingreso y su promedio de calificaciones al final del segundo año. Divide los resultados de los exámenes de ingreso en dos niveles y los promedios de calificaciones en tres niveles. Ordenando los datos de acuerdo a estas divisiones, forma la tabla de contingencia que se muestra como Tabla\(\PageIndex{6}\), en la que ya se han calculado los totales de fila y columna.
| \(GPA\) | |||||
|---|---|---|---|---|---|
| \(<2.7\) | \(2.7\; \; \text{to}\; \; 3.2\) | \(>3.2\) | \(\text{Row Total}\) | ||
| \(CEE\) | \(<1800\) | \ (GPA\)\(<2.7\) "style="vertical-align:middle;" >\(35\) | \ (GPA\)\(2.7\; \; \text{to}\; \; 3.2\) "style="vertical-align:middle;" >\(12\) | \ (GPA\)\(>3.2\) "style="vertical-align:middle;" >\(5\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(52\) |
| \(\geq 1800\) | \ (GPA\)\(<2.7\) "style="vertical-align:middle;" >\(6\) | \ (GPA\)\(2.7\; \; \text{to}\; \; 3.2\) "style="vertical-align:middle;" >\(24\) | \ (GPA\)\(>3.2\) "style="vertical-align:middle;" >\(18\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(48\) | |
| \(\text{Column Total}\) | \ (GPA\)\(<2.7\) "style="vertical-align:middle;" >\(41\) | \ (GPA\)\(2.7\; \; \text{to}\; \; 3.2\) "style="vertical-align:middle;" >\(36\) | \ (GPA\)\(>3.2\) "style="vertical-align:middle;" >\(23\) | \ (\ text {Total de fila}\)” style="vertical-align:middle; ">\(\text{Total}=100\) | |
Prueba, a\(1\%\) nivel de significancia, si estos datos proporcionan evidencia suficiente para concluir que los\(CEE\) puntajes indican niveles de desempeño futuros de estudiantes de primer año universitarios entrantes medidos por\(GPA\).
Solución:
Realizamos la prueba utilizando el enfoque de valor crítico, siguiendo el método habitual de cinco pasos descrito al final de la Sección 8.1.
- Paso 1. Las hipótesis son\[H_0:\text{CEE and GPA are independent factors}\\ vs.\\ H_a:\text{CEE and GPA are not independent factors}\]
- Paso 2. La distribución es chi-cuadrada.
- Paso 3. Para calcular el valor del estadístico de prueba primero debemos calcular el número esperado para cada una de las seis celdas centrales (aquellas cuyas entradas son negritas):
- 1ª fila y 1ª columna:\(E=(R\times C)/n=41\times 52/100=21.32\)
- 1ª fila y 2ª columna:\(E=(R\times C)/n=36\times 52/100=18.72\)
- 1ª fila y 3ª columna:\(E=(R\times C)/n=23\times 52/100=11.96\)
- 2ª fila y 1ª columna:\(E=(R\times C)/n=41\times 48/100=19.68\)
- 2ª fila y 2ª columna:\(E=(R\times C)/n=36\times 48/100=17.28\)
- 2ª fila y 3ª columna:\(E=(R\times C)/n=23\times 48/100=11.04\)
La tabla\(\PageIndex{6}\) se actualiza a Tabla\(\PageIndex{6}\).
| \(GPA\) | |||||
|---|---|---|---|---|---|
| \(<2.7\) | \(2.7\; \; \text{to}\; \; 3.2\) | \(>3.2\) | \(\text{Row Total}\) | ||
| \(CEE\) | \(<1800\) | \ (GPA\)\(<2.7\) "style="vertical-align:middle;” class="lt-stats-513">
\(O=35\) \(E=21.32\) |
\ (GPA\)\(2.7\; \; \text{to}\; \; 3.2\) "style="vertical-align:middle;” class="lt-stats-513">
\(O=12\) \(E=18.72\) |
\ (GPA\)\(>3.2\) "style="vertical-align:middle;” class="lt-stats-513">
\(O=5\) \(E=11.96\) |
\ (\ text {Total de fila}\)” style="vertical-align:middle;” class="lt-stats-513">\(R = 52\) |
| \(\geq 1800\) | \ (GPA\)\(<2.7\) "style="vertical-align:middle;” class="lt-stats-513">
\(O=6\) \(E=19.68\) |
\ (GPA\)\(2.7\; \; \text{to}\; \; 3.2\) "style="vertical-align:middle;” class="lt-stats-513">
\(O=24\) \(E=17.28\) |
\ (GPA\)\(>3.2\) "style="vertical-align:middle;” class="lt-stats-513">
\(O=18\) \(E=11.04\) |
\ (\ text {Total de fila}\)” style="vertical-align:middle;” class="lt-stats-513">\(R = 48\) | |
| \(\text{Column Total}\) | \ (GPA\)\(<2.7\) "style="vertical-align:middle;” class="lt-stats-513">\(C = 41\) | \ (GPA\)\(2.7\; \; \text{to}\; \; 3.2\) "style="vertical-align:middle;” class="lt-stats-513">\(C = 36\) | \ (GPA\)\(>3.2\) "style="vertical-align:middle;” class="lt-stats-513">\(C = 23\) | \ (\ text {Total de fila}\)” style="vertical-align:middle;” class="lt-stats-513">\(n = 100\) | |
El estadístico de prueba es
\[\begin{align*} \chi^2 &= \sum \frac{(O-E)^2}{E}\\ &= \frac{(35-21.32)^2}{21.32}+\frac{(12-18.72)^2}{18.72}+\frac{(5-11.96)^2}{11.96}+\frac{(6-19.68)^2}{19.68}+\frac{(24-17.28)^2}{17.28}+\frac{(18-11.04)^2}{11.04}\\ &= 31.75 \end{align*}\]
- Paso 4. Ya que el\(CEE\) factor tiene dos niveles y el\(GPA\) factor tiene tres,\(I = 2\) y\(J = 3\). Así, el estadístico de prueba sigue la distribución de chi-cuadrado con\(df=(2-1)\times (3-1)=2\) grados de libertad.
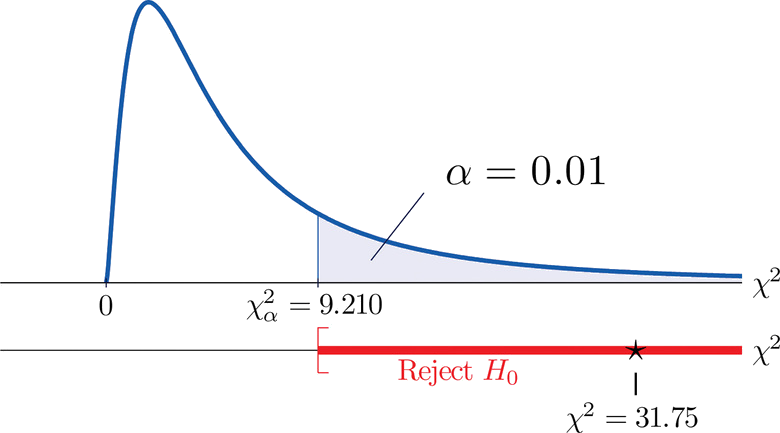
Dado que la prueba es de cola derecha, el valor crítico es\(\chi _{0.01}^{2}\). Leyendo de la Figura 7.1.6 “Valores Críticos de las Distribuciones Chi-Cuadradas”\(\chi _{0.01}^{2}=9.210\), por lo que la región de rechazo es\([9.210,\infty )\).
- Paso 5. Ya que\(31.75 > 9.21\) la decisión es rechazar la hipótesis nula. Ver Figura\(\PageIndex{5}\). Los datos proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir esa\(CEE\) puntuación y no\(GPA\) son independientes: la puntuación del examen de ingreso tiene poder predictivo.
Llave para llevar
- Los valores críticos de una distribución chi-cuadrada con grados de libertad df se encuentran en la Figura 7.1.6.
- Se puede utilizar una prueba de chi-cuadrado para evaluar la hipótesis de que dos variables o factores aleatorios son independientes.

