11.4: Pruebas F en ANOVA de una vía
- Page ID
- 151157
Objetivos de aprendizaje
- Comprender cómo usar una\(F\) prueba para juzgar si varias medias poblacionales son todas iguales
En el capítulo 9, vimos cómo comparar dos medias poblacionales\(\mu _1\) y\(\mu _2\).
En esta sección aprenderemos a comparar tres o más medias poblacionales al mismo tiempo, lo que suele ser de interés en aplicaciones prácticas. Por ejemplo, un administrador de una universidad puede estar interesado en saber si los promedios de calificaciones de los estudiantes son los mismos para diferentes especializaciones. En otro ejemplo, un oncólogo puede estar interesado en saber si los pacientes con el mismo tipo de cáncer tienen los mismos tiempos promedio de supervivencia bajo varios tratamientos diferentes contra el cáncer competidores.
En general, supongamos que hay poblaciones\(K\) normales con medias posiblemente diferentes\(μ_1 , μ_2 , \ldots, μ_K\), pero todas con la misma varianza\(σ^2\). La pregunta del estudio es si todas las medias\(K\) poblacionales son iguales. Formulamos esta pregunta como prueba de hipótesis
\[H_0: \mu _1=\mu _2=\cdots =\mu _K\\ vs.\\ H_a: \text{not all K population means are equal}\]
Para realizar la prueba se toman muestras aleatorias\(K\) independientes de las poblaciones\(K\) normales. Las medias\(K\) muestrales, las\(K\) varianzas de las muestras y los tamaños de las\(K\) muestras se resumen en la tabla:
| Población | Tamaño de la muestra | Media de la Muestra | Varianza de la muestra |
|---|---|---|---|
| \(1\) | \(n_1\) | \(\bar{x_1}\) | \(s_{1}^{2}\) |
| \(2\) | \(n_2\) | \(\bar{x_2}\) | \(s_{2}^{2}\) |
| \(\vdots \) | \(\vdots \) | \(\vdots \) | \(\vdots \) |
| \(K\) | \(n_K\) | \(\bar{x_K}\) | \(s_{K}^{2}\) |
Defina las siguientes cantidades:
Definiciones
El tamaño combinado de la muestra:
\[n=n_1+n_2+ \ldots + n_K\]
La media de la muestra combinada de todas las\(n\) observaciones:
\[x= \dfrac{\displaystyle Σx}{n} = \dfrac{n_1 \overline{x} + n_2 \overline{x}_2 + \ldots + n_K \overline{x}_K}{n}\]
El cuadrado medio para el tratamiento:
\[MST=\dfrac{n_1(\overline{x}_1−\overline{x})^2 + n_2(\overline{x}_2−\overline{x})^2 + \ldots + n_K (\overline{x}K−\overline{x})^2}{K−1}\]
El cuadrado medio para el error:
\[MSE= \dfrac{(n_1−1)s^2_1 + (n_2−1)s^2_2 + \ldots + (n_{K−1})s^2_K}{n−K}\]
\(MST\)se puede considerar como la varianza entre las muestras aleatorias independientes\(K\) individuales y\(MSE\) como la varianza dentro de las muestras. Esta es la razón del nombre “análisis de varianza”, ANOVA universalmente abreviado. El adjetivo “unidireccional” tiene que ver con que el esquema de muestreo es el más sencillo posible, el de tomar una muestra aleatoria de cada población considerada. Si las medias de las\(K\) poblaciones son todas iguales entonces las dos cantidades\(MST\) y\(MSE\) deben estar cerca de las mismas, por lo que la hipótesis nula será rechazada si la relación de estas dos cantidades es significativamente mayor que\(1\). Esto arroja el siguiente estadístico de prueba y métodos y condiciones para su uso.
Estadística de prueba para probar la hipótesis nula que\(K\) Population Means Are Equal
\[F =\dfrac{MST}{MSE}\]
Si las\(K\) poblaciones se distribuyen normalmente con una varianza común y si\(H_0: \mu _1=\mu _2=\cdots =\mu _K\) es verdadera entonces bajo muestreo aleatorio independiente sigue\(F\) aproximadamente una\(F\) -distribución con grados de libertad\(df_1=K-1\) y\(df_2=n-K\).
La prueba es de cola derecha:\(H_0\) se rechaza a nivel de significancia α si\(F≥F_α\).
Como siempre la prueba se realiza utilizando el procedimiento habitual de cinco pasos.
Ejemplo\(\PageIndex{1}\)
El promedio de los promedios de calificaciones (GPA) de los cursos universitarios en una especialización específica es una medida de dificultad de la mayor. Un educador desea realizar un estudio para averiguar si los niveles de dificultad de las distintas carreras son los mismos. Para tal estudio, se selecciona una muestra aleatoria de los promedios principales de calificaciones (GPA) de los estudiantes de último año que se\(11\) gradúan en una universidad grande para cada una de las cuatro carreras de matemáticas, inglés, educación y biología. Los datos se dan en la Tabla\(\PageIndex{1}\). Pruebe, a\(5\%\) nivel de significancia, si los datos contienen evidencia suficiente para concluir que existen diferencias entre los GPA mayores promedio de estas cuatro mayores.
| Matemáticas | Inglés | Educación | Biología |
|---|---|---|---|
| 2.59 | 3.64 | 4.00 | 2.78 |
| 3.13 | 3.19 | 3.59 | 3.51 |
| 2.97 | 3.15 | 2.80 | 2.65 |
| 2.50 | 3.78 | 2.39 | 3.16 |
| 2.53 | 3.03 | 3.47 | 2.94 |
| 3.29 | 2.61 | 3.59 | 2.32 |
| 2.53 | 3.20 | 3.74 | 2.58 |
| 3.17 | 3.30 | 3.77 | 3.21 |
| 2.70 | 3.54 | 3.13 | 3.23 |
| 3.88 | 3.25 | 3.00 | 3.57 |
| 2.64 | 4.00 | 3.47 | 3.22 |
Solución:
- Paso 1. La prueba de hipótesis es\[H_0: \mu _1=\mu _2=\mu _3=\mu _4\\ vs.\\ H_a: \text{not all four population means are equal}\; @\; \alpha =0.05\]
- Paso 2. El estadístico de prueba es\(F=MST/MSE\) con (desde\(n=44\) y\(K=4\)) grados de libertad\(df_1=K-1=4-1=3\) y\(df_2=n-K=44-4=40\).
- Paso 3. Si indexamos la población de las carreras de matemáticas por\(1\), las especializaciones de inglés por\(2\), las carreras de educación por\(3\), y las carreras de biología por\(4\), entonces los tamaños de muestra, las medias muestrales y las varianzas muestrales de las cuatro muestras en la Tabla\(\PageIndex{1}\) se resumen (después del redondeo por simplicidad) por:
| Mayor | Tamaño de la muestra | Media de la Muestra | Varianza de la muestra |
|---|---|---|---|
| Matemáticas | \(n_1=11\) | \(\bar{x_1}=2.90\) | \(s_{1}^{2}=0.188\) |
| Inglés | \(n_2=11\) | \(\bar{x_2}=3.34\) | \(s_{2}^{2}=0.148\) |
| Educación | \(n_3=11\) | \(\bar{x_3}=3.36\) | \(s_{3}^{2}=0.229\) |
| Biología | \(n_4=11\) | \(\bar{x_4}=3.02\) | \(s_{4}^{2}=0.157\) |
El promedio de todas\(44\) las observaciones es (después del redondeo por simplicidad)\(\overline{x}=3.15\). Calculamos (redondeo para simplificar)
\[\begin{align} MST &= \dfrac{11(2.90−3.15)^2+11(3.34−3.15)^2+11(3.36−3.15)^2+11(3.02−3.15)^2}{4−1} \nonumber \\[6pt] &=\dfrac{1.7556}{3} \nonumber \\[6pt] &=0.585 \nonumber \end{align}\]
y
\[\begin{align} MSE &= \dfrac{(11−1)(0.188)+(11−1)(0.148)+(11−1)(0.229)+(11−1)(0.157)}{44−4} \nonumber \\[6pt] &=\dfrac{7.22}{40} \nonumber \\[6pt] &=0.181 \nonumber \end{align}\]
para que
\[F=\dfrac{MST}{MSE}=\dfrac{0.585}{0.181}=3.232\]
- Paso 4. La prueba es de cola derecha. El único valor crítico es (desde\(df_1=3\) y\(df_2=40\))\(F_\alpha =F_{0.05}=2.84\). Así, la región de rechazo es\([2.84,\infty )\), como se ilustra en la Figura\(\PageIndex{1}\).
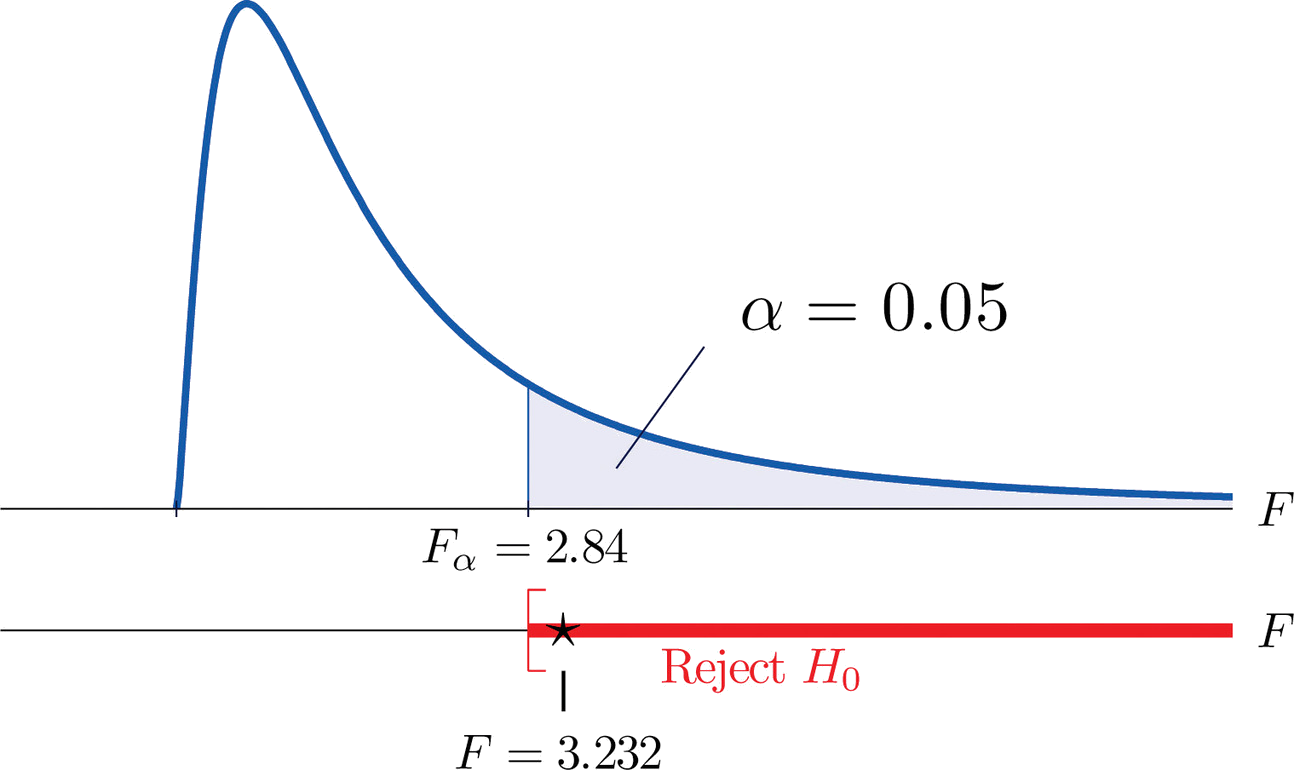
- Paso 5. Ya que\(F=3.232>2.84\), rechazamos\(H_0\). Los datos proporcionan evidencia suficiente, a\(5\%\) nivel de significancia, para concluir que los promedios de los GPA principales para las cuatro mayores consideradas no son todos iguales.
Ejemplo\(\PageIndex{2}\): Mice Survival Times
Un laboratorio de investigación desarrolló dos tratamientos que se cree que tienen el potencial de prolongar los tiempos de supervivencia de los pacientes con una forma aguda de leucemia tímica. Para evaluar los efectos potenciales del tratamiento, los ratones de\(33\) laboratorio con leucemia tímica se dividieron aleatoriamente en tres grupos. Un grupo recibió Tratamiento\(1\), uno recibió Tratamiento\(2\) y el tercero se observó como grupo control. Los tiempos de supervivencia de estos ratones se dan en la Tabla\(\PageIndex{2}\). Pruebe, a\(1\%\) nivel de significancia, si estos datos proporcionan evidencia suficiente para confirmar la creencia de que al menos uno de los dos tratamientos afecta el tiempo promedio de supervivencia de ratones con leucemia tímica.
| Tratamiento\(1\) | Tratamiento\(2\) | Control | |
|---|---|---|---|
| \ (1\) ">71 | 75 | \ (2\) ">77 | 81 |
| \ (1\) ">72 | 73 | \ (2\) ">67 | 79 |
| \ (1\) ">75 | 72 | \ (2\) ">79 | 73 |
| \ (1\) ">80 | 65 | \ (2\) ">78 | 71 |
| \ (1\) ">60 | 63 | \ (2\) ">81 | 75 |
| \ (1\) ">65 | 69 | \ (2\) ">72 | 84 |
| \ (1\) ">63 | 64 | \ (2\) ">71 | 77 |
| \ (1\) ">78 | 71 | \ (2\) ">84 | 67 |
| \ (1\) "> | \ (2\) ">91 | ||
Solución:
- Paso 1. La prueba de hipótesis es\[H_0: \mu _1=\mu _2=\mu _3\\ vs.\\ H_a: \text{not all three population means are equal}\; @\; \alpha =0.01\]
- Paso 2. El estadístico de prueba es\(F=\dfrac{MST}{MSE}\) con (desde\(n=33\) y\(K=3\)) grados de libertad\(df_1=K-1=3-1=2\) y\(df_2=n-K=33-3=30\).
- Paso 3. Si indexamos la población de ratones que reciben Tratamiento\(1\) por\(1\), Tratamiento\(2\) por\(2\), y sin tratamiento por\(3\), entonces los tamaños de muestra, medias de muestra, y varianzas de muestra de las tres muestras en la Tabla\(\PageIndex{2}\) se resumen (después del redondeo por simplicidad) por:
| Grupo | Tamaño de la muestra | Media de la Muestra | Varianza de la muestra |
|---|---|---|---|
| Tratamiento\(1\) | \(n_1=16\) | \(\bar{x_1}=69.75\) | \(s_{1}^{2}=34.47\) |
| Tratamiento\(2\) | \(n_2=9\) | \(\bar{x_2}=77.78\) | \(s_{2}^{2}=52.69\) |
| Control | \(n_3=8\) | \(\bar{x_3}=75.88\) | \(s_{3}^{2}=30.69\) |
El promedio de todas\(33\) las observaciones es (después del redondeo por simplicidad)\(\overline{x}=73.42\). Calculamos (redondeo para simplificar)
\[\begin{align*} MST &= \frac{16(69.75-73.42)^2+9(77.78-73.42)^2+8(75.88-73.42)^2}{31}\\ &= \frac{434.63}{2}\\ &= 217.50 \end{align*}\]
y
\[\begin{align*} MSE &= \frac{(16-1)(34.47)+(9-1)(52.69)+(8-1)(30.69)}{33-3}\\ &= \frac{1153.4}{30}\\ &= 38.45\end{align*}\]
para que
\[F=\dfrac{MST}{MSE}=\dfrac{217.50}{38.45}=5.65\]
- Paso 4. La prueba es de cola derecha. El único valor crítico es\(F_\alpha =F_{0.01}=5.39\). Así, la región de rechazo es\([5.39,\infty )\), como se ilustra en la Figura\(\PageIndex{2}\).
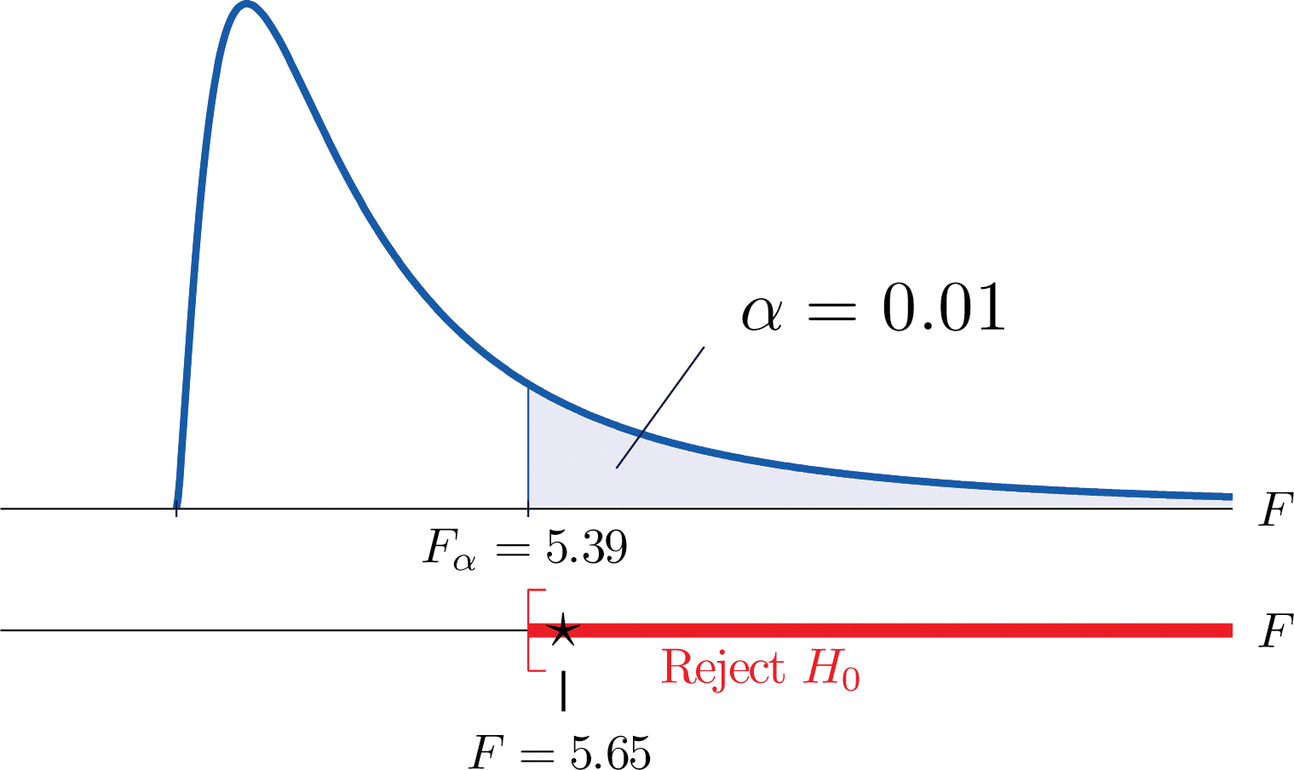
- Paso 5. Ya que\(F=5.65>5.39\), rechazamos\(H_0\). Los datos proporcionan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que existe un efecto de tratamiento al menos para uno de los dos tratamientos en el aumento del tiempo medio de supervivencia de ratones con leucemia tímica.
Es importante señalar que, si se rechaza la hipótesis nula de medias iguales de población, la implicación estadística es que no todas las medias poblacionales son iguales. Sin embargo, no dice qué media poblacional es diferente de cuál. La inferencia sobre dónde radica la diferencia sugerida se realiza con mayor frecuencia mediante un estudio de seguimiento.
Llave para llevar
- Se puede utilizar una\(F\) prueba para evaluar la hipótesis de que las medias de varias poblaciones normales, todas con la misma desviación estándar, son idénticas.

