18.3: Poder Estadístico

Recuerde del capítulo anterior que bajo el enfoque de prueba de hipótesis de Neyman-Pearson, tenemos que especificar nuestro nivel de tolerancia para dos tipos de errores: Falsos positivos (que llamaron error Tipo I) y falsos negativos (a los que llamaron error Tipo II). La gente a menudo se enfoca mucho en el error Tipo I, porque hacer una afirmación de falso positivo generalmente se ve como algo muy malo; por ejemplo, las afirmaciones ahora desacreditadas de Wakefield (1999) de que el autismo se asoció con la vacunación llevaron a un sentimiento anti-vacuna que ha resultado en aumentos sustanciales en enfermedades infantiles como el sarampión. Del mismo modo, no queremos afirmar que un medicamento cura una enfermedad si realmente no lo hace Es por eso que la tolerancia a los errores de Tipo I generalmente se establece bastante baja, generalmente en$\ alfa = 0.05$. Pero ¿qué pasa con los errores de Tipo II?

El concepto de poder estadístico es el complemento del error Tipo II, es decir, es la probabilidad de encontrar un resultado positivo dado que existe:

$$potencia = 1 -\ beta$$

Otro aspecto importante del modelo de Neyman-Pearson que no discutimos anteriormente es el hecho de que además de especificar los niveles aceptables de errores Tipo I y Tipo II, también tenemos que describir una hipótesis alternativa específica, es decir, ¿cuál es el tamaño del efecto que deseamos detectar? De lo contrario, no podemos interpretar$\ beta$— la probabilidad de encontrar un efecto grande siempre va a ser mayor que encontrar un efecto pequeño, por lo que$\ beta$será diferente dependiendo del tamaño del efecto que estemos tratando de detectar.

Hay tres factores que pueden afectar el poder:

• Tamaño de la muestra: Las muestras más grandes proporcionan mayor potencia estadística
• Tamaño del efecto: Un diseño dado siempre tendrá mayor poder para encontrar un efecto grande que un efecto pequeño (porque encontrar efectos grandes es más fácil)
• Tasa de error Tipo I: Existe una relación entre el error Tipo I y la potencia tal que (siendo todo lo demás igual) disminuir el error de Tipo I también disminuirá la potencia.

Esto lo podemos ver a través de la simulación. Primero simulemos un solo experimento, en el que comparamos las medias de dos grupos usando una prueba t estándar. Variaremos el tamaño del efecto (especificado en términos de la d de Cohen), la tasa de error de Tipo I y el tamaño de la muestra, y para cada uno de estos examinaremos cómo se ve afectada la proporción de resultados significativos (es decir, potencia). La Figura 18.4 muestra un ejemplo de cómo cambia la potencia en función de estos factores.

Figura 18.4: Resultados de la simulación de potencia, mostrando la potencia en función del tamaño de la muestra, con tamaños de efecto mostrados como diferentes colores y alfa como tipo de línea. El criterio estándar de 80 por ciento de potencia se muestra mediante la línea punteada negra.

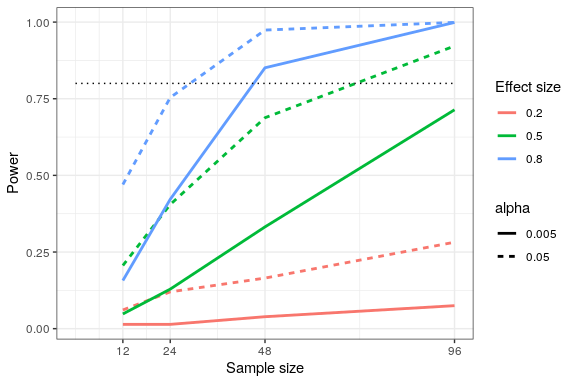
Esta simulación nos muestra que incluso con un tamaño de muestra de 96, tendremos relativamente poco poder para encontrar un efecto pequeño ($d = 0.2$) con$\ alfa = 0.005$. Esto significa que un estudio diseñado para hacer esto sería inútil —es decir, casi se garantiza que no encontrará nada aunque exista un verdadero efecto de ese tamaño.

Hay al menos dos razones importantes para preocuparnos por el poder estadístico, una de las cuales discutimos aquí y la otra a la que volveremos en el Capítulo 32. Si eres investigador, probablemente no quieras pasar tu tiempo haciendo experimentos inútiles. Ejecutar un estudio con poca potencia es esencialmente inútil, porque significa que hay una probabilidad muy baja de que uno encuentre un efecto, aunque exista.

18.3.1 Análisis de potencia

Afortunadamente, hay herramientas disponibles que nos permiten determinar el poder estadístico de un experimento. El uso más común de estas herramientas es en la planificación de un experimento, cuando nos gustaría determinar qué tan grande debe ser nuestra muestra para tener el poder suficiente para encontrar nuestro efecto de interés.

Digamos que nos interesa realizar un estudio de cómo un rasgo de personalidad particular difiere entre usuarios de dispositivos iOS versus Android. Nuestro plan es recolectar dos grupos de individuos y medirlos en el rasgo de personalidad, para luego comparar los dos grupos usando una prueba t. Para determinar el tamaño de muestra necesario, podemos usar la función pwr.t.test () de la biblioteca pwr:

## 
##      Two-sample t test power calculation 
## 
##               n = 64
##               d = 0.5
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Esto nos dice que necesitaríamos al menos 64 sujetos en cada grupo para tener el poder suficiente para encontrar un efecto de tamaño mediano. Siempre es importante realizar un análisis de potencia antes de comenzar un nuevo estudio, para asegurarse de que el estudio no será inútil debido a una muestra que es demasiado pequeña.

Se te podría haber ocurrido que si el tamaño del efecto es lo suficientemente grande, entonces la muestra necesaria será muy pequeña. Por ejemplo, si ejecutamos el mismo análisis de potencia con un tamaño de efecto de d=2, entonces veremos que solo necesitamos alrededor de 5 sujetos en cada grupo para tener la potencia suficiente para encontrar la diferencia.

## 
##      Two-sample t test power calculation 
## 
##               n = 5.1
##               d = 2
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Sin embargo, es raro en la ciencia estar haciendo un experimento en el que esperamos encontrar un efecto tan grande, así como no necesitamos estadísticas que nos digan que los niños de 16 años son más altos que los de 6 años. Cuando realizamos un análisis de potencia, necesitamos especificar un tamaño de efecto que sea plausible para nuestro estudio, que generalmente provendría de investigaciones previas. No obstante, en el Capítulo 32 discutiremos un fenómeno conocido como la “maldición del ganador” que probablemente dé como resultado que los tamaños de los efectos publicados sean mayores que el tamaño del efecto verdadero, por lo que esto también debe tenerse en cuenta.