1.4: Órdenes Parciales
- Page ID
- 152076
Los órdenes parciales son una clase especial de relaciones que juegan un papel importante en la teoría de la probabilidad.
Teoría Básica
Un orden parcial en un conjunto\(S\) es una relación\(\preceq\)\(S\) que es reflexiva, antisimétrica y transitiva. El par\( (S, \preceq) \) se llama conjunto parcialmente ordenado. Así que para todos\( x, \ y, \ z \in S \):
- \( x \preceq x \), la propiedad reflexiva
- Si\( x \preceq y \) y\( y \preceq x \) entonces\( x = y \), la propiedad antisimétrica
- Si\( x \preceq y \) y\( y \preceq z \) entonces\( x \preceq z \), la propiedad transitiva
Como sugieren el nombre y la notación, un orden parcial es un tipo de ordenación de los elementos de\(S\). Los órdenes parciales ocurren naturalmente en muchas áreas de las matemáticas, incluida la probabilidad. Un orden parcial en un conjunto da lugar naturalmente a varias otras relaciones en el set.
Supongamos que\( \preceq \) es un orden parcial en un conjunto\( S \). Las relaciones\(\succeq\),,\(\prec\),\(\succ\)\(\perp\), y\(\parallel\) se definen de la siguiente manera:
- \(x \succeq y\)si y sólo si\(y \preceq x\).
- \(x \prec y\)si y sólo si\(x \preceq y\) y\(x \ne y\).
- \(x \succ y\)si y sólo si\(y \prec x\).
- \(x \perp y\)si y sólo si\(x \preceq y\) o\(y \preceq x\).
- \(x \parallel y\)si y sólo si ni\( x \preceq y \) ni\( y \preceq x \).
Tenga en cuenta que\( \succeq \) es la inversa de\( \preceq \), y\(\succ \) es la inversa de\( \prec \). Obsérvese también que\( x \preceq y \) si y sólo si cualquiera\( x \prec y \) o\( x = y \), así la relación determina\( \prec \) completamente la relación\( \preceq \). A la relación\(\prec\) se le llama a veces orden parcial estricto o fuerte para distanciarla del orden parcial ordinario (débil)\(\preceq\). Por último, señalar que\( x \perp y \) significa que\( x \) y\( y \) están relacionados en el orden parcial, mientras que\( x \parallel y \) significa que\( x \) y no\( y \) están relacionados en el orden parcial. Así, las relaciones\( \perp \) y\( \parallel \) son complementos entre sí, como conjuntos de pares ordenados. Un orden total o lineal es un orden parcial en el que no hay elementos no relacionados.
Un orden parcial\(\preceq\) on\(S\) es un orden total o un orden lineal si para cada\(x, \ y \in S\), cualquiera\(x \preceq y\) o\(y \preceq x\).
Supongamos que\(\preceq_1\) y\(\preceq_2\) son órdenes parciales en un conjunto\(S\). Entonces\(\preceq_1\) es un suborden de\(\preceq_2\), o equivalentemente\(\preceq_2\) es una extensión de\(\preceq_1\) si y sólo si\(x \preceq_1 y\) implica\( x \preceq_2 y\) para\(x, \ y \in S\).
Por lo tanto, si\( \preceq_1 \) es un suborden de\( \preceq_2 \), entonces como conjuntos de pares ordenados,\(\preceq_1\) es un subconjunto de\(\preceq_2\). Necesitamos una relación más que surja naturalmente de un orden parcial.
Supongamos que\(\preceq\) es un orden parcial en un conjunto\(S\). Porque\(x, \ y \in S\),\(y\) se dice que cubre\(x\) si\(x \prec y\) pero ningún elemento\(z \in S\) satisface\(x \prec z \prec y\).
Si\(S\) es finita, la relación de cobertura determina completamente el orden parcial, en virtud de la propiedad transitiva.
Supongamos que\(\preceq\) es un orden parcial en un conjunto finito\(S\). El gráfico de cobertura o gráfico Hasse de\((S, \preceq)\) es el gráfico dirigido con conjunto de vértices\(S\) y conjunto de bordes dirigidos\(E\), donde\((x, y) \in E\) si y solo si\(y\) cubre\(x\).
Así,\(x \prec y\) si y sólo si hay una ruta dirigida en la gráfica de\(x\) a\(y\). Los gráficos de Hasse llevan el nombre del matemático alemán Helmut Hasse. Las gráficas a menudo se dibujan con los bordes dirigidos hacia arriba. De esta manera, las direcciones se pueden inferir sin tener que dibujar realmente flechas.
Ejemplos Básicos
Por supuesto, el orden ordinario\(\le\) es un orden total en el conjunto de números reales\(\R\). El orden parcial del subconjunto es uno de los más importantes en teoría de probabilidad:
Supongamos que\(S\) es un conjunto. La relación de subconjunto\(\subseteq\) es un orden parcial encendido\(\mathscr{P}(S)\), el conjunto de potencia de\(S\).
Prueba
Demostramos este resultado en la sección de sets. Revisar, recordar que para\( A, \ B \in \mathscr{P}(S) \),\( A \subseteq B \) significa que eso\( x \in A \) implica\( x \in B \). También\( A = B \) significa que\( x \in A \) si y solo si\( x \in B \). Así
- \( A \subseteq A \)
- \( A \subseteq B \)y\( B \subseteq A \) si y solo si\( A = B \)
- \( A \subseteq B \)e\( B \subseteq C \) implica\( A \subseteq C \)
Aquí hay un orden parcial que surge naturalmente de la aritmética.
Dejar\(\mid\) denotar la relación de división en el conjunto de enteros positivos\(\N_+\). Es decir,\(m \mid n\) si y sólo si existe\(k \in \N_+\) tal que\(n = k m\). Entonces
- \(\mid\)es una orden parcial sobre\(\N_+\).
- \(\mid\)es un suborden del orden ordinario\(\le\).
Prueba
- Claramente\( n \mid n \) para\( n \in \N_+ \), ya que\( n = 1 \cdot n \), así\( \mid \) es reflexivo. Supongamos\( m \mid n \) y\( n \mid m \), dónde\( m, \ n \in \N_+ \). Entonces existen\( j, \ k \in \N_+ \) tal que\( n = k m \) y\( m = j n \). Sustituir da\( n = j k n \), y por lo tanto\( j = k = 1 \). \( m = n \)Así\( \mid \) es como es antisimétrico. Por último, supongamos\( m \mid n \) y\( n \mid p \), dónde\( m, \ n, \ p \in \N_+ \). Entonces existe\( j, \ k \in \N_+ \) tal que\( n = j m \) y\( p = k n \). Sustituir da\( p = j k m \), entonces\( m \mid p \). Así\( \mid \) es transitivo.
- Si\( m, \ n \in \N_+ \) y\( m \mid n \), entonces existe\( k \in \N_+ \) tal que\( n = k m \). Ya que\( k \ge 1 \),\( m \le n \).
El conjunto de funciones de un conjunto a un conjunto ordenado parcial se puede ordenar parcialmente de manera natural.
Supongamos que\( S \) es un conjunto y que\( (T, \preceq_T) \) es un conjunto parcialmente ordenado, y vamos a\( \mathscr{S} \) denotar el conjunto de funciones\( f: S \to T \). La relación\( \preceq \) sobre\( \mathscr{S} \) definida por\( f \preceq g \) si y solo\( f(x) \preceq_T g(x) \) para todos\( x \in S \) es un orden parcial on\( \mathscr{S} \).
Prueba
Supongamos que\( f, \, g, \, h \in \mathscr{S} \).
- \( f(x) \preceq_T f(x) \)para todos\( x \in S \), entonces\( f \preceq f \).
- Si\( f \preceq g \) y\( g \preceq f \) entonces\( f(x) \preceq_T g(x) \) y\( g(x) \preceq_T f(x) \) para todos\( x \in S \). De ahí\( f(x) = g(x) \) para todos\( x \in S \) así\( f = g \).
- Si\( f \preceq g \) y\( g \preceq h \) entonces\( f(x) \preceq_T g(x) \) y\( g(x) \preceq_T h(x) \) para todos\( x \in S \). De ahí\( f(x) \preceq_T h(x) \) para todos\( x \in S \) así\( f \preceq h \).
Tenga en cuenta que no necesitamos un orden parcial en el dominio\( S \).
Propiedades Básicas
Las pruebas de las siguientes propiedades básicas son sencillas. Asegúrate de probarlos tú mismo antes de leer los que aparecen en el texto.
La inversa de un orden parcial es también un orden parcial.
Prueba
Claramente se mantienen las propiedades reflexivas, antisimétricas y transitivas\( \succeq \).
Si\(\preceq\) es un orden parcial encendido\(S\) y\(A\) es un subconjunto de\(S\), entonces la restricción de\(\preceq\) a\(A\) es un orden parcial encendido\(A\).
Prueba
Las propiedades reflexivas, antisimétricas y transitivas dadas anteriormente se mantienen para todos\( x, \ y, \ z \in S \) y por lo tanto se mantienen para todos\( x, \ y, \ z \in A \).
El siguiente teorema caracteriza las relaciones que corresponden al orden estricto.
\(S\)Déjese ser un conjunto. Una relación\(\preceq\) es un orden parcial sobre\(S\) si y sólo si\(\prec\) es transitiva e irreflexiva.
Prueba
Supongamos que\( \preceq \) es un orden parcial encendido\( S \). Recordemos que\( \prec \) se define por\( x \prec y \) si y solo si\( x \preceq y \) y\( x \ne y \). Si\( x \prec y \) y\( y \prec z \) entonces\( x \preceq y \) y\( y \preceq z \), y así\( x \preceq z \). Por otro lado, si\( x = z \) entonces\( x \preceq y \) y\( y \preceq x \) así\( x = y \), una contradicción. De ahí\( x \ne z \) y así\(x \prec z\). Por lo tanto,\( \prec \) es transitivo. Si\( x \prec y \) entonces\( x \ne y \) por definición, así\( \prec \) es irreflexivo.
Por el contrario, supongamos que\( \prec \) es una relación transitiva e irreflexiva sobre\( S \). Recordemos que\( \preceq \) se define por\( x \preceq y \) si y solo si\( x \prec y \) o\( x = y \). Por definición entonces,\( \preceq \) es reflexivo:\( x \preceq x \) para cada uno\( x \in S \). A continuación, supongamos que\( x \preceq y \) y\( y \preceq x \). Si\( x \prec y \) y\( y \prec x \) luego\( x \prec x \) por la propiedad transitiva de\( \prec \). Pero esto es una contradicción por la propiedad irreflexiva, así que debemos tener\( x = y \). Así\( \preceq \) es antisimétrico. Supongamos\( x \preceq y \) y\( y \preceq z \). Hay cuatro casos:
- Si\( x \prec y \) y\( y \prec z \) luego\( x \prec z \) por la propiedad transitiva de\( \prec \).
- Si\( x = y \) y\( y \prec z \) luego\( x \prec z \) por sustitución.
- Si\( x \prec y \) y\( y = z \) luego\( x \prec z \) por sustitución.
- Si\( x = y \) y\( y = z \) luego\( x = z \) por la propiedad transitiva de\( = \).
En todos los casos tenemos\( x \preceq z \) así\( \preceq \) es transitivo. De ahí\( \preceq \) que sea un orden parcial sobre\( S \).
Conjuntos y funciones de Monotone
Las órdenes parciales forman un entorno natural para aumentar y disminuir conjuntos y funciones. Aquí están las definiciones:
Supongamos que\(\preceq\) es un orden parcial en un conjunto\(S\) y eso\(A \subseteq S\). En las siguientes definiciones,\(x, \, y\) se encuentran elementos arbitrarios de\(S\).
- \(A\)está aumentando si\(x \in A\) e\(x \preceq y\) implica\(y \in A\).
- \(A\)es decreciente si\(y \in A\) e\(x \preceq y\) implica\(x \in A\).
Supongamos que\(S\) es un conjunto con orden parcial\(\preceq_S\),\(T\) es un conjunto con orden parcial\(\preceq_T\), y eso\(f: S \to T\). En las siguientes definiciones,\(x, \, y\) se encuentran elementos arbitrarios de\(S\).
- \(f\)está aumentando si y sólo si\(x \preceq_S y\) implica\(f(x) \preceq_T f(y)\).
- \(f\)es decreciente si y sólo si\(x \preceq_S y\) implica\(f(x) \succeq_T f(y)\).
- \(f\)está aumentando estrictamente si y sólo si\(x \prec_S y\) implica\(f(x) \prec_T f(y)\).
- \(f\)es estrictamente decreciente si y sólo si\(x \prec_S y\) implica\(f(x) \succ_T f(y)\).
Recordemos la definición de la función indicadora\(\bs{1}_A\) asociada a un subconjunto\( A \) de un conjunto universal\( S \): For\( x \in S \),\( \bs{1}_A(x) = 1 \) if\( x \in A \) y\( \bs{1}_A(x) = 0 \) if\( x \notin A \).
Supongamos que\(\preceq\) es un orden parcial en un conjunto\(S\) y eso\(A \subseteq S\). Entonces
- \(A\)está aumentando si y sólo si\(\boldsymbol{1}_A\) va en aumento.
- \(A\)está disminuyendo si y sólo si\(\boldsymbol{1}_A\) es decreciente.
Prueba
- \( A \)está aumentando si y sólo si\( x \in A \) e\( x \preceq y \) implica\( y \in A \) si y sólo si\( \bs{1}_A(x) = 1 \) e\( x \le y \) implica\( \bs{1}_A(y) = 1 \) si y sólo si\( \bs{1}_A \) va en aumento.
- \( A \)es decreciente si y sólo si\( y \in A \) e\( x \preceq y \) implica\( x \in A \) si y sólo si\( \bs{1}_A(y) = 1 \) e\( x \le y \) implica\( \bs{1}_A(x) = 1 \) si y sólo si\( \bs{1}_A \) es decreciente.
Isomorfismo
Dos conjuntos parcialmente ordenados\( (S, \preceq_S) \) y\( (T, \preceq_T) \) se dice que son isomórficos si existe una función uno a uno\( f \) de\( S \) hacia arriba\( T \) tal que\( x \preceq_S y \) si y solo si\( f(x) \preceq_T f(y) \), para todos\( x, \ y \in S \). La función\( f \) es un isomorfismo.
Generalmente, un espacio matemático a menudo consiste en un conjunto y varias estructuras definidas en términos del conjunto, como relaciones, operadores o una colección de subconjuntos. Hablando vagamente, dos espacios matemáticos del mismo tipo son isomórficos si existe una función uno a uno de uno de los conjuntos sobre el otro que preserva las estructuras, y nuevamente, la función se llama isomorfismo. La idea básica es que los espacios isomórficos son matemáticamente idénticos, a excepción de las cuestiones superficiales de apariencia. La palabra isomorfismo es del griego y significa igual forma.
Supongamos que los conjuntos parcialmente ordenados\( (S, \preceq_S) \) y\( (T, \preceq_T) \) son isomórficos, y eso\( f: S \to T \) es un isomorfismo. Entonces\( f \) y\( f^{-1} \) están aumentando estrictamente.
Prueba
Tenemos que demostrar eso por\( x, \ y \in S \),\( x \prec_S y \) si y solo si\( f(x) \prec_T f(y) \). Si\( x \prec_S y \) entonces por definición,\( f(x) \preceq_T f(y) \). Pero si\( f(x) = f(y) \) entonces\( x = y \) ya\( f \) es uno a uno. Esto es una contradicción, entonces\( f(x) \prec_T f(y) \). Del mismo modo, si\( f(x) \prec_T f(y) \) entonces por definición,\( x \preceq_S y \). Pero si\( x = y \) entonces\( f(x) = f(y) \), una contradicción. De ahí\( x \prec_S y \).
En cierto sentido, el orden parcial del subconjunto es universal, cada conjunto parcialmente ordenado es isomórfico\((\mathscr{S}, \subseteq)\) para alguna colección de conjuntos\(\mathscr{S}\).
Supongamos que\(\preceq\) es un orden parcial en un conjunto\(S\). Entonces existe\( \mathscr{S} \subseteq \mathscr{P}(S) \) tal que\( (S, \preceq) \) es isomórfico a\( (\mathscr{S}, \subseteq)\).
Prueba
Para cada uno\(x \in S\), deja\(A_x = \{u \in S: u \preceq x\}\), y luego deja\(\mathscr{S} = \{A_x: x \in S\}\), para que\(\mathscr{S} \subseteq \mathscr{P}(S)\). Vamos a mostrar que la función\(x \mapsto A_x\) de\(S\) hacia\(\mathscr{S}\) es uno a uno, y satisface\[ x \preceq y \iff A_x \subseteq A_y \] Primero, supongamos que\( x, \ y \in S \) y\( A_x = A_y \). Entonces\( x \in A_x \) así\( x \in A_y \) y por lo tanto\( x \preceq y \). Del mismo modo,\( y \in A_y \) así\( y \in A_x \) y por lo tanto\( y \preceq x \). Así pues\( x = y \), el mapeo es uno a uno. A continuación, supongamos que\( x \preceq y \). Si\( u \in A_x \) entonces es\( u \preceq x \) así\( u \preceq y \) por la propiedad transitiva, y por lo tanto\( u \in A_y \). Por lo tanto\( A_x \subseteq A_y \). Por el contrario, supongamos\( A_x \subseteq A_y \). Como antes,\( x \in A_x \), así\( x \in A_y \) y por lo tanto\( x \preceq y \).
Elementos Extremales
Varios tipos de elementos extremos juegan un papel importante en conjuntos parcialmente ordenados. Aquí están las definiciones:
Supongamos que\(\preceq\) es un orden parcial en un conjunto\(S\) y eso\(A \subseteq S\).
- Un elemento\(a \in A\) es el elemento mínimo de\(A\) si y solo si\(a \preceq x\) por cada\(x \in A\).
- Un elemento\(a \in A\) es un elemento mínimo de\(A\) si y solo si no\(x \in A\) satisface\(x \prec a\).
- Un elemento\(b \in A\) es el elemento máximo de\(A\) si y solo si\(b \succeq x\) por cada\(x \in A\).
- Un elemento\(b \in A\) es un elemento máximo de\(A\) si y solo si no\(x \in A\) satisface\(x \succ b\).
En general, un conjunto puede tener varios elementos máximos y mínimos (o ninguno). Por otra parte,
Los elementos mínimos y máximos de\(A\), si existen, son únicos. Se denotan\(\min(A)\) y\(\max(A)\), respectivamente.
Prueba
Supongamos que\( a, \ b \) son elementos mínimos de\( A \). Ya que\( a, \ b \in A \) tenemos\( a \preceq b \) y\( b \preceq a \), así\( a = b \) por la propiedad antisimétrica. La prueba para el elemento máximo es análoga.
Los elementos mínimos, máximos, mínimos y máximos de un conjunto deben pertenecer a ese conjunto. Las siguientes definiciones se refieren a los límites superior e inferior de un conjunto, que no tienen que pertenecer al conjunto.
Supongamos nuevamente que\( \preceq \) es un orden parcial en un conjunto\( S \) y eso\( A \subseteq S \). Entonces
- Un elemento\(u \in S\) es un límite inferior para\(A\) si y solo si\(u \preceq x\) para cada\(x \in A\).
- Un elemento\(v \in S\) es un límite superior para\(A\) si y solo si\(v \succeq x\) para cada\(x \in A\).
- El mayor límite inferior o infimum de\(A\), si existe, es el máximo del conjunto de límites inferiores de\(A\).
- El límite inferior superior o supremo de\(A\), si existe, es el mínimo del conjunto de límites superiores de\(A\).
Por (20), el mayor límite inferior de\(A\) es único, si existe. Se denota\(\text{glb}(A)\) o\(\inf(A)\). De igual manera, el límite inferior superior de\(A\) es único, si existe, y se denota\(\text{lub}(A)\) o\(\sup(A)\). Tenga en cuenta que cada elemento de\(S\) es un límite inferior y un límite superior para\(\emptyset\), ya que las condiciones en la definición se mantienen vacíamente.
Los símbolos\( \wedge \) y\( \vee \) también se utilizan para infimum y supremum, respectivamente, así\( \bigwedge A = \inf(A) \) y\( \bigvee A = \sup(A) \) si existen.. En particular, for\( x, \ y \in S \), se usa más comúnmente la notación del operador, así\( x \wedge y = \inf\{x, y\} \) y\( x \vee y = \sup\{x, y\} \). Los conjuntos parcialmente ordenados para los que siempre existen estos elementos son importantes, y tienen un nombre especial.
Supongamos que\(\preceq\) es un orden parcial en un conjunto\(S\). Entonces\((S, \preceq)\) es una celosía si\( x \wedge y \) y\( x \vee y \) existe para cada uno\( x, \ y \in S \).
Para el orden parcial del subconjunto, los operadores inf y sup corresponden a intersección y unión, respectivamente:
Dejar\(S\) ser un conjunto y considerar el subconjunto orden parcial\(\subseteq\) encendido\(\mathscr{P}(S)\), el conjunto de potencia de\(S\). Dejar\(\mathscr{A}\) ser un subconjunto no vacío de\(\mathscr{P}(S)\), es decir, una colección no vacía de subconjuntos de\(S\). Entonces
- \(\inf(\mathscr{A}) = \bigcap \mathscr{A}\)
- \(\sup(\mathscr{A}) = \bigcup \mathscr{A}\)
Prueba
- Primero,\( \bigcap \mathscr{A} \subseteq A \) para cada\( A \in \mathscr{A} \) y por lo tanto\( \bigcap \mathscr{A} \) es un límite inferior de\( \mathscr{A} \). Si\( B \) es un límite inferior de\( \mathscr{A} \) entonces\( B \subseteq A \) para cada\( A \in \mathscr{A} \) y por lo tanto\( B \subseteq \bigcap \mathscr{A} \). Por lo tanto,\( \bigcap \mathscr{A} \) es el mayor límite inferior.
- Primero,\(A \subseteq \bigcup \mathscr{A} \) para cada\( A \in \mathscr{A} \) y por lo tanto\( \bigcup \mathscr{A} \) es un límite superior de\( \mathscr{A} \). Si\( B \) es un límite superior de\( \mathscr{A} \) entonces\( A \subseteq B \) para cada\( A \in \mathscr{A} \) y por lo tanto\( \bigcup \mathscr{A} \subseteq B \). Por lo tanto,\( \bigcup \mathscr{A} \) es el límite inferior superior.
En particular,\( A \wedge B = A \cap B \) y\( A \vee B = A \cup B \), también lo\( (\mathscr P(S), \subseteq) \) es una celosía.
Considere el orden parcial de división\(\mid\) en el conjunto de enteros positivos\(\N_+\) y deje\(A\) ser un subconjunto no vacío de\(\N_+\).
- \(\inf(A)\)es el mayor divisor común de\(A\), generalmente denotado\(\gcd(A)\) en este contexto.
- Si\(A\) es infinito entonces\(\sup(A)\) no existe. Si\(A\) es finito entonces\(\sup(A)\) es el múltiplo menos común de\(A\), generalmente denotado\(\text{lcm}(A)\) en este contexto.
Supongamos que\(S\) es un conjunto y eso\(f: S \to S\). Se dice que un elemento\(z \in S\) es un punto fijo de\(f\) si\(f(z) = z\).
El siguiente resultado explora un teorema básico de punto fijo para un conjunto parcialmente ordenado. El teorema es importante en el estudio de la cardinalidad.
Supongamos que\(\preceq\) es un orden parcial en un conjunto\(S\) con la propiedad que\(\sup(A)\) existe para cada uno\(A \subseteq S\). Si\(f: S \to S\) va en aumento, entonces\(f\) tiene un punto fijo.
Prueba.
Dejar\(A = \{x \in S: x \preceq f(x)\}\) y dejar\(z = \sup(A)\). Si\(x \in A\) entonces\(x \preceq z\) es así\(x \preceq f(x) \preceq f(z)\). De ahí\(f(z)\) es un límite superior de\(A\) así\(z \preceq f(z)\). Pero entonces\(f(z) \preceq f\left(f(z)\right)\) así\(f(z) \in A\). De ahí\(f(z) \preceq z\). Por lo tanto\(f(z) = z\).
Obsérvese que las hipótesis del teorema requieren que\(\sup(\emptyset) = \min(S)\) exista. El conjunto no\(A = \{x \in S: x \preceq f(x)\}\) está vacío desde\(\min(S) \in A\).
Si\( \preceq \) es un orden total en un conjunto\( S \) con la propiedad que cada subconjunto no vacío de\( S \) tiene un elemento mínimo, entonces\( S \) se dice que está bien ordenado por\( \preceq \). Uno de los ejemplos más importantes es\( \N_+ \), que está bien ordenado por el orden ordinario\( \le \). Por otra parte, el principio de ordenación del pozo, que equivale al axioma de elección, establece que cada conjunto no vacío puede estar bien ordenado.
Pedidos en espacios de productos
Supongamos que\(S\) y\(T\) son conjuntos con órdenes parciales\(\preceq_S\) y\(\preceq_T\) respectivamente. Definir la relación\(\preceq\) en\(S \times T\) por\((x, y) \preceq (z, w)\) si y solo si\(x \preceq_S z\) y\(y \preceq_T w\).
- La relación\(\preceq\) es un pedido parcial sobre\(S \times T\), llamado, apropiadamente, el pedido del producto.
- Supongamos que\((S, \preceq_S) = (T, \preceq_T)\). Si\(S\) tiene al menos 2 elementos, entonces no\(\preceq\) es un pedido total encendido\(S^2\).
Prueba
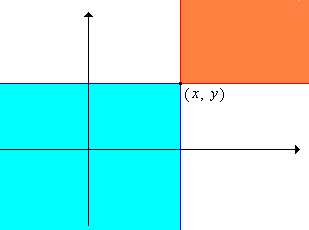
El orden del producto se extiende de manera directa al producto cartesiano de una secuencia finita o infinita de espacios parcialmente ordenados. Por ejemplo, supongamos que\( S_i \) es un conjunto con orden parcial\( \preceq_i \) para cada uno\( i \in \{1, 2, \ldots, n\} \), donde\( n \in \N_+ \). El pedido del producto\( \preceq \) en el juego de productos\( S_1 \times S_2 \times \cdots \times S_n \) se define de la siguiente manera: para\( \bs{x} = (x_1, x_2, \ldots, x_n) \) y\( \bs{y} = (y_1, y_2, \ldots, y_n) \) en el conjunto de productos,\( \bs{x} \preceq \bs{y} \) si y solo si\( x_i \preceq_i y_i \) para cada uno\( i \in \{1, 2, \ldots, n\} \). Podemos generalizar esto más a conjuntos de productos arbitrarios. Supongamos que\( S_i \) es un conjunto para cada uno\( i \) en un conjunto de índices no vacío (ambos por lo demás arbitrarios)\( I \). Recordemos que\[ \prod_{i \in I} S_i = \left\{x: x \text{ is a function from } I \text{ into } \bigcup_{i \in I } S_i \text{ such that } x(i) \in S_i \text{ for each } i \in I \right\}\] Para que la notación se vea más como un producto cartesiano simple, escribiremos\( x_i \) en lugar de\( x(i) \) para el valor de una función\( x \) en el conjunto de productos en\( i \in I \).
Supongamos que\( S_i \) es un conjunto con orden parcial\( \preceq_i \) para cada uno\( i \) en un conjunto de índices no vacíos\( I \). Definir la relación\( \preceq \) sobre\( \prod_{i \in I} S_i \) por\( x \preceq y \) si y solo si\( x_i \preceq_i y_i \) para cada uno\( i \in I \). Entonces\( \preceq \) se realiza un pedido parcial en el conjunto de productos, conocido nuevamente como el pedido del producto.
Prueba
A pesar de la abstracción, la prueba es perfectamente sencilla. Supongamos que\( x, \, y, \, z \in \prod_{i \in I} S_i \).
- \( x_i \preceq_i x_i \)para cada\( i \in I \), y por lo tanto\( x \preceq x \). Así\( \preceq \) es reflexivo.
- Supongamos que\( x \preceq y \) y\( y \preceq x \). Entonces\( x_i \preceq_i y_i \) y\( y_i \preceq_i x_i \) para cada uno\( i \in I \). De ahí\( x_i = y_i \) para cada uno\( i \in I \) y así\( x = y \). Así\( \preceq \) es antisimétrico
- Supongamos que\( x \preceq y \) y\( y \preceq z \). Entonces\( x_i \preceq_i y_i \) y\( y_i \preceq_i z_i \) para cada uno\( i \in I \). De ahí\( x_i \preceq_i z_i \) para cada uno\( i \in I \), así\( x \preceq z \). Así\( \preceq \) es transitivo.
Obsérvese nuevamente que no se hacen suposiciones sobre el conjunto de índices\( I \), salvo que sea no vacío. En particular, no es necesario ordenar el\( I \). El siguiente resultado da un tipo de pedido muy diferente en un espacio de producto.
Supongamos de nuevo que\(S\) y\(T\) son conjuntos con órdenes parciales\(\preceq_S\) y\(\preceq_T\) respectivamente. Definir la relación\(\preceq\) en\(S \times T\) por\((x, y) \preceq (z, w)\) si y solo si cualquiera\(x \prec_S z\), o\(x = z\) y\(y \preceq_T w\).
- La relación\(\preceq\) es un orden parcial sobre\(S \times T\), llamado orden lexicográfico o orden de diccionario.
- Si\(\preceq_S\) y\(\preceq_T\) son pedidos totales en\(S\) y\(T\), respectivamente, entonces\(\preceq\) es un pedido total encendido\(S \times T\).
Prueba
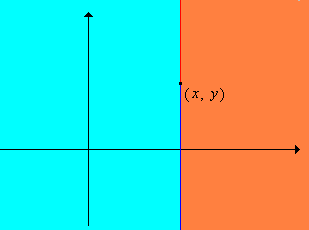
Al igual que con el pedido del producto, el orden lexicográfico puede generalizarse a una colección de espacios parcialmente ordenados. Sin embargo, necesitamos que el conjunto de índices esté totalmente ordenado.
Supongamos que\( S_i \) es un conjunto con orden parcial\( \preceq_i \) para cada uno\( i \) en un conjunto de índices no vacíos\( I \). Supongamos también que\( \le \) es un pedido total encendido\( I \). Defina la relación\( \preceq \) en el conjunto de productos de la\( \prod_{i \in I} S_i \) siguiente manera:\( x \prec y \) si y solo si existe\( j \in I \) tal que\( x_i = y_i \) si\( i \lt j \) y\( x_j \prec_j y_j \). Entonces
- \( \preceq \)es un orden parcial encendido\( S \), conocido nuevamente como el orden lexicográfico.
- Si\( \preceq_i \) es un pedido total para cada uno\( i \in I \), y\( I \) está bien ordenado por\( \le \), entonces\( \preceq \) es un pedido total encendido\( S \).
Prueba
- Por el resultado en órdenes fuertes, necesitamos demostrar que\( \prec \) es irreflexivo y transitivo. Primero, no\( x \in \prod_{i \in I} S_i\) satisface\( x \prec x \) ya que\( x_i = x_i \) para todos\( i \in I \). De ahí\( \prec \) que sea irreflexivo. A continuación, supongamos que\( x, \ y, \ z \in \prod_{i \in I} S_i \) y eso\( x \prec y \) y\( y \prec z \). Entonces existe\( j \in I \) tal que\( x_i = y_i \) si\( i \lt j \) y\( x_j \prec_j y_j \). De igual manera, existe\( k \in I \) tal que\( y_i = z_i \) si\( i \lt k \) y\( y_k \prec_k z_k \). Nuevamente, ya que\( I \) está totalmente ordenado, ya sea\( j \lt k \) o\( k \lt j \) o\( j = k \). Si\( j \lt k \), entonces\( x_i = y_i = z_i \) si\( i \lt j \) y\( x_j \prec_j y_j = z_j \). Si\( k \lt j \), entonces\( x_i = y_i = z_i \) si\( i \lt k \) y\( x_k = y_k \prec_k z_k \). Si\( j = k \), entonces\( x_i = y_i = z_i \) si\( i \lt j \) y\( x_j \prec_j y_j \prec_j z_j \). En todos los casos,\( x \prec z \) así\( \prec \) es transitivo.
- Supongamos ahora que\( \preceq_i \) es un pedido total encendido\( S_i \) para cada uno\( i \in I \) y que\( I \) está bien ordenado por\( \le \). Déjalo\( x, \ y \in \prod_{i \in I} S_i \) con\( x \ne y \). Vamos\( J = \{i \in I: x_i \ne y_i\} \). Entonces\( J \ne \emptyset\) por suposición, y por lo tanto tiene un elemento mínimo\( j \). Si\( i \lt j \) entonces\( i \notin J \) y por lo tanto\( x_i = y_i \). Por otro lado,\( x_j \ne y_j \) ya que\( j \in J \) y por lo tanto, ya que\( \preceq_j \) está totalmente ordenado, debemos tener cualquiera\( x_j \prec_j y_j \) o\( y_j \prec_j x_j \). En el primer caso,\( x \prec y \) y en el segundo\( y \prec x \). De ahí\( \preceq \) que esté totalmente ordenado.
El término lexicográfico proviene de la forma en que ordenamos las palabras alfabéticamente: Miramos la primera letra; si estas son diferentes, sabemos ordenar las palabras. Si las primeras letras son iguales, miramos la segunda letra; si estas son diferentes, sabemos ordenar las palabras. Seguimos de esta manera hasta encontrar letras que son diferentes, y podemos ordenar las palabras. De hecho, el orden lexicográfico es a veces referido como el primer orden de diferencia. Tenga en cuenta también que si\( S_i \) es un conjunto y\( \preceq_i \) un pedido total encendido\( S_i \) para\( i \in I \), entonces por el principio de ordenamiento de pozos, existe un orden bien\( \le \) de\( I \), y por lo tanto existe un pedido total lexicográfico en el espacio del producto\( \prod_{i \in I} S_i \). Como estructura matemática, el orden lexicográfico no es tan oscuro como se podría pensar.
\( (\R, \le) \)es isomórfico al producto lexicográfico de\( (\Z, \le) \) con\( \left([0, 1), \le\right) \), donde\( \le \) está el orden ordinario para los números reales.
Prueba
Cada se\( x \in \R \) puede expresar de manera única en la forma\( x = n + t \) donde\( n = \lfloor x \rfloor \in \Z \) está la parte entera y\( t = x - n \in [0, 1) \) es el resto. Así\( x \mapsto (n, t) \) es una función uno a uno desde\( \R \) hacia\( \Z \times [0, 1) \). Por ejemplo,\( 5.3 \) mapas a\( (5, 0.3) \), mientras que\( -6.7 \) mapas a\( (-7, 0.3) \). Supongamos que\( x = m + s, \ y = n + t \in \R \), donde por supuesto\( m, \, n \in \Z \) están las partes enteras de\( x \) y\( y \), respectivamente, y\( s, \, t \in [0, 1) \) son los restos correspondientes. Entonces\( x \lt y \) si y sólo si\( m \lt n \) o\( m = n \) y\( s \lt t \). Nuevamente, para ilustrar con números reales reales, podemos decir que con\( 5.3 \lt 7.8 \) solo comparar las partes enteras:\( 5 \lt 7 \). Podemos ignorar los restos. Por otro lado, para ver que\( 6.4 \lt 6.7 \) necesitamos comparar los restos:\( 0.4 \lt 0.7 \) ya que las partes enteras son las mismas.
Límites de Secuencias de Números Reales
Supongamos que\((a_1, a_2, \ldots)\) es una secuencia de números reales.
La secuencia\(\inf\{a_n, a_{n+1} \ldots\}\) está aumentando en\(n \in \N_+\).
Dado que la secuencia de infimums en el último resultado va en aumento, el límite existe en\( \R \cup \{\infty\} \), y se llama el límite inferior de la secuencia original:\[ \liminf_{n \to \infty} a_n = \lim_{n \to \infty} \inf \{a_n, a_{n+1}, \ldots\} \]
La secuencia\(\sup\{a_n, a_{n+1}, \ldots \}\) está disminuyendo en\(n \in \N_+\).
Dado que la secuencia de supremas en el último resultado es decreciente, el límite existe en\( \R \cup\{-\infty\} \), y se llama el límite superior de la secuencia original:\[ \limsup_{n \to \infty} a_n = \lim_{n \to \infty} \sup\{a_n, a_{n+1}, \ldots \} \] Tenga en cuenta que\(\liminf_{n \to \infty} a_n \le \limsup_{n \to \infty} a_n\) y la igualdad se mantiene si y solo si\(\lim_{n \to \infty} a_n\) existe (y es el valor común).
Espacios vectoriales de funciones
Supongamos que\( S \) es un conjunto no vacío, y recuerda que el conjunto\( \mathscr{V} \) de funciones\( f: S \to \R \) es un espacio vectorial, bajo la definición puntual habitual de suma y multiplicación escalar. Como se señala en (9), también\( \mathscr{V} \) es un conjunto ordenado parcial, bajo el orden parcial puntual:\( f \preceq g \) si y solo si\( f(x) \le g(x) \) para todos\( x \in S \). Consistente con las definiciones (19),\( f \in \mathscr{V} \) está acotada si existe\( C \in (0, \infty) \) tal que\( \left|f(x)\right| \le C \) para todos\( x \in S \). Ahora vamos a\( \mathscr{U} \) denotar el conjunto de funciones delimitadas\( f: S \to \R \), y para\( f \in \mathscr{U} \) definir\[ \|f\| = \sup\{\left|f(x)\right|: x \in S\} \]
\( \mathscr{U} \)es un subespacio vectorial de\( \mathscr{V} \) y\( \| \cdot \| \) es una norma sobre\( \mathscr{U} \).
Prueba
Para demostrar que\( \mathscr{U} \) es un subespacio, solo hay que señalar que está cerrado bajo suma y multiplicación escalar. Es decir, si\( f, \, g: S \to \R \) están acotados, y si\( c \in \R \), entonces\( f + g \) y\( c f \) están acotados. A continuación mostramos que\( \| \cdot \| \) satisface los axiomas de una norma. Nuevamente, vamos\( f, \, g \in \mathscr{U} \) y\( c \in \R \)
- Claramente\( \|f\| \ge 0 \) y\( \|f\| = 0 \) si y solo si\( f(x) = 0 \) para todos\( x \in S \) si y solo si\( f = \bs{0} \), el cero funciona encendido\( S \).
- \( \| c f\| = \sup\left\{\left|c f(x) \right|: x \in S\right\} = \left|c\right| \sup\left\{\left|f(x)\right|: x \in S\right\} = \left|c\right| \|f\| \)
- Por el triángulo habitual la desigualdad en\( \R \),\( \left|f(x) + g(x) \right| \le \left|f(x)\right| + \left|g(x)\right| \) para\( x \in S \). De ahí\[ \sup\left\{\left|f(x) + g(x)\right|: x \in S\right\} \le \sup\left\{\left|f(x)\right| + \left|g(x)\right|: x \in S\right\} \le \sup\left\{\left|f(x)\right|: x \in S\right\} + \sup\left\{\left|g(x)\right|: x \in S\right\} \] que sea,\( \|f + g\| \le \|f\| + \|g\| \).
Recordemos que la parte (a) es la propiedad positiva, la parte (b) es la propiedad de escalado y la parte (c) es la desigualdad del triángulo.
Suficientemente apropiado,\( \| \cdot \| \) se llama la norma suprema sobre\( \mathscr{U} \). Los espacios vectoriales de funciones acotadas, de valor real, con la norma suprema son especialmente importantes en los procesos probabilísticos y aleatorios. Volveremos nuevamente a esta discusión en las secciones avanzadas sobre espacios métricos y teoría de medidas.
Ejercicios Computacionales
Vamos\(S = \{2, 3, 4, 6, 12\}\).
- Dibuje la gráfica de Hasse correspondiente al orden ordinario\(\le\) en\(S\).
- Dibuje la gráfica de Hasse correspondiente al orden parcial de división\(\mid\) en\(S\).
Contestar
-
La gráfica de Hasse\( (S, \le) \) 
-
La gráfica de Hasse\( (S, |) \) 
Considera el orden ordinario\(\le\) en el conjunto de números reales\(\R\), y deja\(A = [a, b)\) dónde\(a \lt b\). Encuentra cada uno de los siguientes que existen:
- El conjunto de elementos mínimos de\(A\)
- El conjunto de elementos máximos de\(A\)
- \(\min(A)\)
- \(\max(A)\)
- El conjunto de límites inferiores de\(A\)
- El conjunto de límites superiores de\(A\)
- \(\inf(A)\)
- \(\sup(A)\)
Contestar
- \(\{a\}\)
- \(\emptyset\)
- \(a\)
- No existe
- \((-\infty, a]\)
- \([b, \infty)\)
- \(a\)
- \(b\)
De nuevo considerar el orden parcial de división\(\mid\) en el conjunto de enteros positivos\(\N_+\) y dejar\(A = \{2, 3, 4, 6, 12\}\). Encuentra cada uno de los siguientes que existen:
- El conjunto de elementos mínimos de\(A\)
- El conjunto de elementos máximos de\(A\)
- \(\min(A)\)
- \(\max(A)\)
- El conjunto de límites inferiores de\(A\)
- El conjunto de límites superiores de\(A\)
- \(\inf(A)\)
- \(\sup(A)\).
Contestar
- \(\{2, 3\}\)
- \(\{12\}\)
- No existe
- \(12\)
- \(\{1\}\)
- \(\{12, 24, 36, \ldots\}\)
- \(1\)
- \(12\)
Vamos\( S = \{a, b, c\} \).
- Dar\( \mathscr{P}(S) \) en forma de lista.
- Describir la gráfica de Hasse de\( (\mathscr{P}(S), \subseteq) \)
Contestar
- \( \mathscr{P}(S) = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, S\} \)
- Para\( A \in \mathscr{P}(S) \) y\( x \in S \setminus A \), hay un borde dirigido de\( A \) a\( A \cup \{x\} \)
Tenga en cuenta que la gráfica de Hasse\( \supseteq \) se ve igual que la gráfica de\( \subseteq \), a excepción de las etiquetas en los vértices. Esta simetría se debe a la relación de complemento.
Vamos\( S = \{a, b, c, d\} \).
- Dar\( \mathscr{P}(S) \) en forma de lista.
- Describir la gráfica de Hasse de\( (\mathscr{P}(S), \subseteq) \)
Contestar
- \( \mathscr{P}(S) = \{\emptyset, \{a\}, \{b\}, \{c\}, \{d\}, \{a, b\}, \{a, c\}, \{a, d\}, \{b, c\}, \{b, d\}, \{c, d\}, \{a, b, c\}, \{a, b, d\}, \{a, c, d\}, \{b, c, d\}, S\} \)
- Para\( A \in \mathscr{P}(S) \) y\( x \in S \setminus A \), hay un borde dirigido de\( A \) a\( A \cup \{x\} \)
Obsérvese nuevamente que la gráfica de Hasse de se\( \supseteq \) ve igual que la gráfica de\( \subseteq \), a excepción de las etiquetas en los vértices. Esta simetría se debe a que la relación de complemento.
Supongamos que\( A \) y\( B \) son subconjuntos de un conjunto universal\( S \). Let\( \mathscr{A} \) denotar la colección de los 16 subconjuntos de los\( S \) que se pueden construir a partir\( A \) y\( B \) usando las operaciones de conjunto. Demostrar que\( (\mathscr{A}, \subseteq) \) es isomórfico al conjunto parcialmente ordenado en el ejercicio anterior. Use la aplicación Diagrama Venn para ayudar.
Prueba
Vamos\( a = A \cap B \),\( b = A \cap B^c \),\( c = A^c \cap B \),\( d = A^c \cap B^c \). Nuestra suposición básica es que\( A \) y\( B \) están en posición general
, por lo que\( a, \, b, \, c, \, d \) son distintas y no vacías. Tenga en cuenta también que\( \{a, b, c, d\} \) las particiones\( S \). Ahora, mapee cada subconjunto\( \mathscr{S} \) de\( \{a, b, c, d\} \) a\( \bigcup \mathscr{S} \). Esta función es un isomorfismo de\( \mathscr{S} \) a\( \mathscr{A} \). Es decir, para\( \mathscr{S} \) y\( \mathscr{T} \) subconjuntos de\( \{a, b, c, d\} \),\( \mathscr{S} \subseteq \mathscr{T} \) si y solo si\( \bigcup \mathscr{S} \subseteq \bigcup \mathscr{T} \).


