2.3: Medidas de probabilidad
- Page ID
- 152168
Esta sección contiene el ingrediente final y más importante en el modelo básico de un experimento aleatorio. Si eres un nuevo estudiante de probabilidad, omita los detalles técnicos.
Definiciones e interpretaciones
Supongamos que tenemos un experimento aleatorio con espacio muestral\( (S, \mathscr S) \), así que ese\( S \) es el conjunto de resultados del experimento y\( \mathscr S \) es la colección de eventos. Cuando ejecutamos el experimento, un evento dado ocurre\( A \) o no ocurre, dependiendo de si el resultado del experimento está en\( A \) o no. Intuitivamente, la probabilidad de un evento es una medida de la probabilidad de que ocurra el evento cuando ejecutamos el experimento. Matemáticamente, la probabilidad es una función en la colección de eventos que satisface ciertos axiomas.
Definición
Una medida de probabilidad (o distribución de probabilidad)\(\P\) en el espacio muestral\( (S, \mathscr S) \) es una función de valor real definida en la colección de eventos\( \mathscr S \) que satisface los siguientes axiomas:
- \(\P(A) \ge 0\)para cada evento\(A\).
- \(\P(S) = 1\).
- Si\(\{A_i: i \in I\}\) es una colección disjunta contable, por pares, de eventos, entonces\[\P\left(\bigcup_{i \in I} A_i\right) = \sum_{i \in I}\P(A_i)\]
Detalles
Recordemos que\( \mathscr S \) se requiere que la colección de eventos sea un\( \sigma \) álgebra, lo que garantiza que la unión de los eventos en (c) es en sí misma un evento. Una medida de probabilidad es un caso especial de una medida positiva.
El axioma (c) se conoce como aditividad contable, y establece que la probabilidad de una unión de una colección finita o contablemente infinita de eventos disjuntos es la suma de las probabilidades correspondientes. A los axiomas se les conoce como los axiomas de Kolmogorov, en honor a Andrei Kolmogorov quien fue el primero en formalizar la teoría de la probabilidad de manera axiomática. De manera más informal, decimos que\( \P \) es una medida de probabilidad (o distribución) sobre\( S \),\( \mathscr S \) generalmente se entiende la colección de eventos.
Los axiomas (a) y (b) son realmente solo una cuestión de convención; elegimos medir la probabilidad de un evento con un número entre 0 y 1 (en contraposición, digamos, a un número entre\(-5\) y\(7\)). El axioma (c) sin embargo, es fundamental e ineludible. Se requiere para probabilidad precisamente por la misma razón que se requiere para otras medidas del tamaño
de un conjunto, como cardinalidad para conjuntos finitos, longitud para subconjuntos de\(\R\), área para subconjuntos de\(\R^2\), y volumen para subconjuntos de\(\R^3\). En todos estos casos, el tamaño de un conjunto que está compuesto por contablemente muchas piezas disjuntas es la suma de los tamaños de las piezas.
Por otro lado, la aditividad incontable (la extensión del axioma (c) a un conjunto de índices incontables\(I\)) no es razonable para la probabilidad, tal como lo es para otras medidas. Por ejemplo, un intervalo de longitud positiva en\(\R\) es una unión de incontables muchos puntos, cada uno de los cuales tiene longitud 0.
Ahora hemos definido los tres ingredientes esenciales para el modelo de un experimento aleatorio:
Un espacio de probabilidad\( (S, \mathscr S, \P) \) consiste en
- Un conjunto de resultados\(S\)
- Una colección de eventos\(\mathscr{S}\)
- Una medida de probabilidad\(\P\) en el espacio muestral\( (S, \mathscr S) \)
Detalles
Nuevamente, la colección de eventos\( \mathscr S \) es un\( \sigma \) álgebra, de manera que el espacio muestral\( (S, \mathscr S) \) es un espacio medible. El espacio de probabilidad\( (S, \mathscr S, \P) \) es un caso especial de un espacio de medida positiva.
La Ley de los Grandes Números
Intuitivamente, se supone que la probabilidad de un evento mide la frecuencia relativa a largo plazo del evento; de hecho, este concepto fue tomado como la definición de probabilidad por Richard Von Mises. Aquí están las definiciones relevantes:
Supongamos que el experimento se repite indefinidamente, y eso\( A \) es un evento. Para\( n \in \N_+ \),
- Vamos a\( N_n(A) \) denotar el número de veces que\( A \) ocurrió. Esta es la frecuencia de\( A \) en las primeras\( n \) carreras.
- Vamos\( P_n(A) = N_n(A) / n \). Esta es la frecuencia relativa o probabilidad empírica de\( A \) en las primeras\( n \) corridas.
Tenga en cuenta que repetir el experimento original de forma indefinida crea un nuevo experimento compuesto, y eso\( N_n(A) \) y\( P_n(A) \) son variables aleatorias para el nuevo experimento. En particular, los valores de estas variables son inciertos hasta que el experimento es\( n \) tiempos de ejecución. La idea básica es que si hemos elegido la medida de probabilidad correcta para el experimento, entonces en cierto sentido esperamos que la frecuencia relativa de un evento converja con la probabilidad del evento. Es decir,\[P_n(A) \to \P(A) \text{ as } n \to \infty, \quad A \in \mathscr S\] independientemente de la incertidumbre de las frecuencias relativas de la izquierda. El enunciado preciso de esto es la ley de los grandes números o la ley de los promedios, uno de los teoremas fundamentales en la probabilidad. Para enfatizar el punto, señalar que en general habrá muchas posibles medidas de probabilidad para un experimento, en el sentido de los axiomas. Sin embargo, solo la medida de probabilidad que modela correctamente el experimento satisfará la ley de grandes números.
Dados los datos de las\( n \) series del experimento, la función de probabilidad empírica\(P_n\) es una medida de probabilidad en\( S \).
Prueba
Si ejecutamos los\( n \) tiempos del experimento, generamos\( n \) puntos en\( S \) (aunque por supuesto, algunos de estos puntos pueden ser los mismos). La función\( A \mapsto N_n(A) \) para\( A \subseteq S \) es simplemente contar la medida correspondiente a los\( n \) puntos. Claramente\( P_n(A) \ge 0 \) para un evento\( A \) y\( P_n(S) = n / n = 1 \). La aditividad contable se mantiene por la regla de suma para la medida de conteo.
La distribución de una variable aleatoria
Supongamos ahora que\(X\) es una variable aleatoria para el experimento, tomando valores en un conjunto\(T\). Recordemos que matemáticamente,\( X \) es una función desde\( S \) dentro\( T \), y\( \{X \in B\}\) denota el evento\(\{s \in S: X(s) \in B\} \) para\( B \subseteq T \). Intuitivamente,\( X \) es una variable de interés para el experimento, y cada declaración significativa sobre\( X \) define un evento.
La función\(B \mapsto \P(X \in B)\) para\( B \subseteq T \) define una medida de probabilidad en\(T\).
Prueba
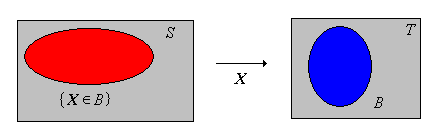.png)
La medida de probabilidad en (5) se llama la distribución de probabilidad de\(X\), por lo que tenemos todos los ingredientes para un nuevo espacio de probabilidad.
Una variable aleatoria\(X\) con valores en\( T \) define un nuevo espacio de probabilidad:
- \(T\)es el conjunto de resultados.
- Los subconjuntos de\( T \) son los eventos.
- La distribución de probabilidad de\(X\) es la medida de probabilidad en\( T \).
Este espacio de probabilidad corresponde al nuevo experimento aleatorio en el que se encuentra el resultado\( X \). Además, recordemos que el resultado del experimento en sí puede pensarse como una variable aleatoria. En concreto, si\(T = S\) dejamos que\(X\) sea la función de identidad encendida\(S\), así que\( X(s) = s \) para\( s \in S \). Entonces\(X\) es una variable aleatoria con valores en\( S \) y\(\P(X \in A) = \P(A)\) para cada evento\( A \). Así, cada medida de probabilidad puede considerarse como la distribución de una variable aleatoria.
Construcciones
Medidas
¿Cómo podemos construir medidas de probabilidad? Como se señaló brevemente anteriormente, existen otras medidas del tamaño
de los conjuntos; en muchos casos, estas se pueden convertir en medidas de probabilidad. Primero, una medida positiva\(\mu\) en el espacio muestral\((S, \mathscr S)\) es una función de valor real definida en\(\mathscr{S}\) que satisface los axiomas (a) y (c) en (1), y luego\( (S, \mathscr S, \mu) \) es un espacio de medida. En general,\(\mu(A)\) se permite que sea infinito. Sin embargo, si\(\mu(S)\) es positivo y finito (por lo que\( \mu \) es una medida positiva finita), entonces se\(\mu\) puede volver a escalar fácilmente en una medida de probabilidad.
Si\(\mu\) es una medida positiva\(S\) con\(0 \lt \mu(S) \lt \infty\) entonces\(\P\) se define a continuación es una medida de probabilidad. \[\P(A) = \frac{\mu(A)}{\mu(S)}, \quad A \in \mathscr S\]
Prueba
- \(\P(A) \ge 0\)desde\(\mu(A) \ge 0\) y\(0 \lt \mu(S) \lt \infty\).
- \(\P(S) = \mu(S) \big/ \mu(S) = 1\)
- Si\(\{A_i: i \in I\}\) es una colección contable de eventos disjuntos entonces\[ \P\left(\bigcup_{i \in I} A_i \right) = \frac{1}{\mu(S)} \mu\left(\bigcup_{i \in I} A_i \right) = \frac{1}{\mu(S)} \sum_{i \in I} \mu(A_i) = \sum_{i \in I} \frac{\mu(A_i)}{\mu(S)} = \sum_{i \in I} \P(A_i) \]
En este contexto,\(\mu(S)\) se llama la constante normalizadora. En las dos subsecciones siguientes, consideramos algunos casos especiales muy importantes.
Distribuciones Discretas
En esta discusión, asumimos que el espacio muestral\((S, \mathscr S)\) es discreto. Recordemos que esto significa que el conjunto de resultados\(S\) es contable y que\(\mathscr S = \mathscr P(S)\) es la colección de todos los subconjuntos de\(S\), de manera que cada subconjunto es un evento. La medida estándar en un espacio discreto es la medida de conteo\(\#\), por lo que ese\(\#(A)\) es el número de elementos en\(A\) para\(A \subseteq S\). Cuando\( S \) es finita, la medida de probabilidad correspondiente a la medida de conteo construida anteriormente es particularmente importante en experimentos combinatorios y de muestreo.
Supongamos que\(S\) es un conjunto finito, no vacío. La distribución uniforme discreta en\(S\) viene dada por\[\P(A) = \frac{\#(A)}{\#(S)}, \quad A \subseteq S\]
El modelo subyacente es arbitrado como el modelo de probabilidad clásico, porque históricamente los primeros problemas de probabilidad (que involucran monedas y dados) se ajustan a este modelo.
En el caso discreto general, si\(\P\) es una medida de probabilidad on\(S\), entonces dado que\( S \) es contable, se deduce de la aditividad contable que\(\P\) está completamente determinada por sus valores en los eventos singleton. Específicamente, si definimos\(f(x) = \P\left(\{x\}\right)\) para\(x \in S\), entonces\(\P(A) = \sum_{x \in A} f(x)\) para cada\(A \subseteq S\). Por axioma (a),\(f(x) \ge 0\) para\(x \in S\) y por axioma (b),\(\sum_{x \in S} f(x) = 1\). Por el contrario, podemos dar una construcción general para definir una medida de probabilidad en un espacio discreto.
Supongamos que\( g: S \to [0, \infty) \). Entonces\(\mu\) definido por\( \mu(A) = \sum_{x \in A} g(x) \) for\( A \subseteq S \) es una medida positiva sobre\(S\). Si\(0 \lt \mu(S) \lt \infty\) entonces\(\P\) se define de la siguiente manera es una medida de probabilidad en\(S\). \[ \P(A) = \frac{\mu(A)}{\mu(S)} = \frac{\sum_{x \in A} g(x)}{\sum_{x \in S} g(x)}, \quad A \subseteq S\]
Prueba
Trivialmente\(\mu(A) \ge 0\) para\( A \subseteq S \) ya no\(g\) es negativo. La propiedad de aditividad contable se mantiene ya que los términos en una suma de números no negativos se pueden reordenar de ninguna manera sin alterar la suma. Por lo tanto, dejar\(\{A_i: i \in I\}\) ser una colección contable de subconjuntos disjuntos de\( S \), y let\(A = \bigcup_{i \in I} A_i\) entonces\[ \mu(A) = \sum_{x \in A} g(x) = \sum_{i \in I} \sum_{x \in A_i} g(x) = \sum_{i \in I} \mu(A_i) \] Si\( 0 \lt \mu(S) \lt \infty \) entonces\( \P \) es una medida de probabilidad escalando el resultado anterior.
En el contexto de nuestras observaciones anteriores,\(f(x) = g(x) \big/ \mu(S) = g(x) \big/ \sum_{y \in S} g(y)\) para\( x \in S \). Se dice que las distribuciones de este tipo son discretas. Las distribuciones discretas se estudian en detalle en el capítulo sobre Distribuciones.
Si\(S\) es finito y\(g\) es una función constante, entonces la medida de probabilidad\(\P\) asociada con\( g \) es la distribución uniforme discreta on\(S\).
Prueba
Supongamos que\(g(x) = c\) para\(x \in S\) donde\(c \gt 0\). Entonces\(\mu(A) = c \#(A) \) y por lo tanto\(\P(A) = \mu(A) \big/ \mu(S) = \#(A) \big/ \#(S)\) para\( A \subseteq S \).
Distribuciones continuas
Las distribuciones de probabilidad que construiremos a continuación son distribuciones continuas\( n \in \N_+ \) y requieren algún cálculo.\( \R^n \)
Para\(n \in \N_+\), la medida estándar\( \lambda_n \) on\( \R^n \) viene dada por\[\lambda_n(A) = \int_A 1 \, dx, \quad A \subseteq \R^n\] En particular,\( \lambda_1(A) \) es la longitud de (A\ subseteq\ R\),\( lambda_2(A) \) es el área de\( A \subseteq \R^2 \), y\( \lambda_3(A) \) es el volumen de\( A \subseteq \R^3 \).
Detalles
Técnicamente,\( \lambda_n \) es Lebesgue medida en los subconjuntos medibles de\( \R^n \), llamado así por Henri Lebesgue. La representación anterior en términos de la integral ordinaria de Riemann de cálculo es válida para los subconjuntos que suelen ocurrir en las aplicaciones. Como es habitual, se supone que todos\( \R^n \) los subconjuntos de la discusión a continuación son adecuados.
Cuando\(n \gt 3\), a veces\(\lambda_n(A)\) se llama el volumen\(n\) -dimensional de\(A \subseteq \R_n\). La medida de probabilidad asociada\( \lambda_n \) a un conjunto con volumen positivo, finito\( n \) dimensional es particularmente importante.
Supongamos que\(S \subseteq \R_n\) con\(0 \lt \lambda_n(S) \lt \infty\). La distribución uniforme continua en\( S \) se define por\[\P(A) = \frac{\lambda_n(A)}{\lambda_n(S)}, \quad A \subseteq S\]
Obsérvese que la distribución uniforme continua es análoga a la distribución uniforme discreta definida en (8), pero con la medida de Lebesgue\( \lambda_n \) reemplazando la medida de conteo\( \# \). Podemos generalizar esta construcción para producir muchas otras distribuciones.
Supongamos otra vez eso\( S \subseteq \R^n\) y aquello\( g: S \to [0, \infty) \). Entonces\( \mu \) definido por\( \mu(A) = \int_A g(x) \, dx \) for\( A \subseteq S \) es una medida positiva sobre\( S \). Si\(0 \lt \mu(S) \lt \infty\), entonces\( \P \) se define de la siguiente manera es una medida de probabilidad en\( S \). \[\P(A) = \frac{\mu(A)}{\mu(S)} = \frac{\int_A g(x) \, dx}{\int_S g(x) \, dx}, \quad A \in \mathscr S\]
Prueba
Técnicamente, la integral en la definición de\(\mu(A)\) es la integral de Lebesgue, pero esta integral concuerda con la integral ordinaria de Riemann de cálculo cuando\(g\) y\(A\) son suficientemente agradables. Se supone que la función\(g\) es medible y es la función de densidad de\(\mu\) con respecto a\(\lambda_n\). Aparte de los tecnicismos, la prueba es sencilla:
- \( \mu(A) \ge 0 \)porque\( A \subseteq S \) ya no\( g \) es negativo.
- Si\(\{A_i: i \in I\}\) se trata de una colección disjunta contable de subconjuntos de\(S\) y\(A = \bigcup_{i \in I} A_i\), entonces, por una propiedad básica de la integral,\[\mu(A) = \int_A g(x) \, dx = \sum_{i \in I} \int_{A_i} g(x) \, dx = \sum_{i \in I} \mu(A_i)\]
Si\( 0 \lt \mu(S) \lt \infty \) entonces\( \P \) es una medida de probabilidad\( S \) por el resultado de escalado anterior.
Se dice que las distribuciones de este tipo son continuas. Las distribuciones continuas se estudian en detalle en el capítulo sobre Distribuciones. Obsérvese que la distribución continua anterior es análoga a la distribución discreta en (9), pero con integrales reemplazando sumas. La teoría general de la integración nos permite unificar estos dos casos especiales, y muchos otros además.
Reglas de Probabilidad
Reglas Básicas
Supongamos nuevamente que tenemos un experimento aleatorio modelado por un espacio de probabilidad\( (S, \mathscr S, \P) \), de modo que ese\(S\) es el conjunto de resultados,\( \mathscr S \) la colección de eventos y\( \P \) la medida de probabilidad. En los siguientes teoremas,\(A\) y\(B\) son eventos. Los resultados siguen fácilmente desde los axiomas de probabilidad en (1), así que asegúrate de probar las pruebas tú mismo antes de leer las del texto.
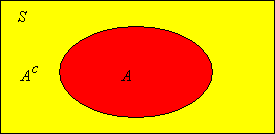
\(\P(A^c) = 1 - \P(A)\). Esto se conoce como la regla del complemento.
Prueba
\(\P(\emptyset) = 0\).
Prueba
Esto se desprende de la regla del complemento a la que se aplica\(A = S\).
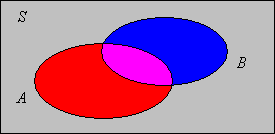
\(\P(B \setminus A) = \P(B) - \P(A \cap B)\). Esto se conoce como la regla de la diferencia.
Prueba
Si\(A \subseteq B\) entonces\(\P(B \setminus A) = \P(B) - \P(A)\).
Prueba
Este resultado es un corolario de la regla de diferencia. Tenga en cuenta que\(A \cap B = A\).
Recordemos que si\( A \subseteq B \) a veces escribimos\( B - A \) para la diferencia establecida, en lugar de\( B \setminus A \). Con esta notación, la regla de diferencia tiene la forma agradable\( \P(B - A) = \P(B) - \P(A) \).
Si\(A \subseteq B\) entonces\(\P(A) \le \P(B)\).
Prueba
Este resultado es un corolario del resultado anterior. Tenga en cuenta eso\( \P(B \setminus A) \ge 0 \) y por lo tanto\( \P(B) - \P(A) \ge 0 \).
Así,\(\P\) es una función creciente, relativa al orden parcial del subconjunto en la colección de eventos\( \mathscr S \), y el orden ordinario en\(\R\). En particular, se deduce que\(\P(A) \le 1\) para cualquier acontecimiento\(A\).
Supongamos que\(A \subseteq B\).
- Si\(\P(B) = 0\) entonces\(\P(A) = 0\).
- Si\(\P(A) = 1\) entonces\(\P(B) = 1\).
Prueba
Esto se deduce inmediatamente de la propiedad creciente en el último teorema.
Las desigualdades de Boole y Bonferroni
El siguiente resultado se conoce como la desigualdad de Boole, que lleva el nombre de George Boole. La desigualdad da un simple límite superior sobre la probabilidad de una unión.
Si\(\{A_i: i \in I\}\) es una colección contable de eventos entonces\[\P\left( \bigcup_{i \in I} A_i \right) \le \sum_{i \in I} \P(A_i)\]
Prueba
Intuitivamente, la desigualdad de Boole se mantiene porque partes del sindicato se han medido más de una vez en la suma de las probabilidades de la derecha. Por supuesto, la suma de las probabilidades puede ser mayor a 1, en cuyo caso la desigualdad de Boole no ayuda. El siguiente resultado es una simple consecuencia de la desigualdad de Boole.
Si\(\{A_i: i \in I\}\) es una colección contable de eventos con\(\P(A_i) = 0\) para cada uno\(i \in I\), entonces\[\P\left( \bigcup_{i \in I} A_i \right) = 0\]
Se dice que un evento\(A\) con\(\P(A) = 0\) es nulo. Así, una unión contable de eventos nulos sigue siendo un evento nulo.
El siguiente resultado se conoce como la desigualdad de Bonferroni, que lleva el nombre de Carlo Bonferroni. La desigualdad da un límite inferior simple para la probabilidad de una intersección.
Si\(\{A_i: i \in I\}\) es una colección contable de eventos entonces\[\P\left( \bigcap_{i \in I} A_i \right) \ge 1 - \sum_{i \in I}\left[1 - \P(A_i)\right]\]
Prueba
Por la ley de De Morgan,\( \left(\bigcap_{i \in I} A_i\right)^c = \bigcup_{i \in I} A_i^c \). De ahí que por la desigualdad de Boole,\[ \P\left[\left(\bigcap_{i \in I} A_i\right)^c\right] \le \sum_{i \in I} \P(A_i^c) = \sum_{i \in I} \left[1 - \P(A_i)\right] \] Usar la regla del complemento vuelve a dar la desigualdad de Bonferroni.
Por supuesto, el límite inferior en la desigualdad de Bonferroni puede ser menor o igual a 0, en cuyo caso no ayuda. El siguiente resultado es una simple consecuencia de la desigualdad de Bonferroni.
Si\(\{A_i: i \in I\}\) es una colección contable de eventos con\(\P(A_i) = 1\) para cada uno\(i \in I\), entonces\[\P\left( \bigcap_{i \in I} A_i \right) = 1\]
Un evento\(A\) con a veces\(\P(A) = 1\) se llama casi seguro o casi seguro. Así, una intersección contable de eventos casi seguros sigue siendo casi segura.
Supongamos que\(A\) y\(B\) son eventos en un experimento.
- Si\(\P(A) = 0\), entonces\(\P(A \cup B) = \P(B)\).
- Si\(\P(A) = 1\), entonces\(\P(A \cap B) = \P(B)\).
Prueba
- Usando la creciente propiedad y la desigualdad de Boole que tenemos\( \P(B) \le \P(A \cup B) \le \P(A) + \P(B) = \P(B) \)
- Usando la creciente propiedad y la desigualdad de Bonferonni tenemos\( \P(B) = \P(A) + \P(B) - 1 \le \P(A \cap B) \le P(B) \)
La regla de partición
Supongamos que\(\{A_i: i \in I\}\) es una colección contable de eventos que particionan\(S\). Recordemos que esto significa que los hechos son disjuntos y su unión lo es\(S\). Para cualquier evento\(B\),\[\P(B) = \sum_{i \in I} \P(A_i \cap B)\]
Prueba
Naturalmente, este resultado es útil cuando se conocen las probabilidades de las intersecciones. Las particiones suelen surgir en relación con una variable aleatoria. Supongamos que\(X\) es una variable aleatoria que toma valores en un conjunto contable\(T\), y que\(B\) es un evento. Entonces\[\P(B) = \sum_{x \in T} \P(X = x, B)\] En esta fórmula, tenga en cuenta que la coma actúa como el símbolo de intersección en la fórmula anterior.
La regla de inclusión-exclusión
Las fórmulas de inclusión-exclusión proporcionan un método para calcular la probabilidad de una unión de eventos en términos de las probabilidades de las diversas intersecciones de los eventos. La fórmula es útil porque a menudo las probabilidades de las intersecciones son más fáciles de calcular. Curiosamente, sin embargo, la misma fórmula funciona para computar la probabilidad de una intersección de eventos en términos de las probabilidades de las diversas uniones de los eventos. Esta versión rara vez se afirma, porque simplemente no es tan útil. Empezamos con dos eventos.
Si\( A, \, B \) son eventos que n\(\P(A \cup B) = \P(A) + \P(B) - \P(A \cap B)\).
Prueba
.png)
Aquí está el resultado complementario para la intersección en términos de uniones:
Si\( A, \, B \) son eventos entonces\(\P(A \cap B) = \P(A) + \P(B) - \P(A \cup B)\).
Prueba
Esto se deduce inmediatamente de la fórmula anterior estar reordenando los términos
A continuación consideramos tres eventos.
Si\( A, \, B, \, C \) son eventos entonces\(\P(A \cup B \cup C) = \P(A) + \P(B) + \P(C) - \P(A \cap B) - \P(A \cap C) - \P(B \cap C) + \P(A \cap B \cap C)\).
Prueba Analítica
Primero tenga en cuenta que\( A \cup B \cup C = (A \cup B) \cup [C \setminus (A \cup B)] \). El evento entre paréntesis y el evento entre corchetes son disjuntos. Así, usando el axioma de aditividad y la regla de diferencia,\[ \P(A \cup B \cup C) = \P(A \cup B) + \P(C) - \P\left[C \cap (A \cup B)\right] = \P(A \cup B) + \P(C) - \P\left[(C \cap A) \cup (C \cap B)\right] \] Usando la regla de inclusión-exclusión para dos eventos (dos veces) tenemos\[ \P(A \cup B \cup C) = \P(A) + \P(B) - \P(A \cap B) + \P(C) - \left[\P(C \cap A) + \P(C \cap B) - \P(A \cap B \cap C)\right] \]
Comprobante por contabilidad
Aquí está el resultado complementario para la probabilidad de una intersección en términos de las probabilidades de los sindicatos:
Si\( A, \, B, \, C \) son eventos entonces\(\P(A \cap B \cap C) = \P(A) + \P(B) + \P(C) - \P(A \cup B) - \P(A \cup C) - \P(B \cup C) + \P(A \cup B \cup C)\).
Prueba
Esto se deduce de resolver for\( \P(A \cap B \cap C) \) en el resultado anterior, y luego usar el resultado para dos eventos en\( \P(A \cap B) \),\( \P(B \cap C) \), y\( \P(A \cap C) \).
Las fórmulas de inclusión-exclusión para dos y tres eventos pueden generalizarse a\(n\) eventos. Para lo que resta de esta discusión, supongamos que\( \{A_i: i \in I\} \) es una colección de eventos donde\( I \) se establece un índice con\( \#(I) = n \).
La fórmula general de inclusión-exclusión para la probabilidad de una unión. \[\P\left( \bigcup_{i \in I} A_i \right) = \sum_{k = 1}^n (-1)^{k - 1} \sum_{J \subseteq I, \; \#(J) = k} \P\left( \bigcap_{j \in J} A_j \right)\]
Prueba por inducción
La prueba es por inducción en\(n\). Ya hemos establecido la fórmula para\( n = 2 \) y\( n = 3 \). Así, supongamos que la fórmula de inclusión-exclusión se mantiene para un dado\( n \), y supongamos que\( (A_1, A_2, \ldots, A_{n+1}) \) es una secuencia de\( n + 1 \) eventos. Entonces\[ \bigcup_{i=1}^{n + 1} A_i = \left(\bigcup_{i=1}^n A_i \right) \cup \left[ A_{n+1} \setminus \left(\bigcup_{i=1}^n A_i\right) \right] \] como antes, el evento entre paréntesis y el evento entre corchetes son disjuntos. Así, usando el axioma de aditividad, la regla de diferencia, y la regla distributiva que tenemos\[ \P\left(\bigcup_{i=1}^{n+1} A_i\right) = \P\left(\bigcup_{i=1}^n A_i\right) + \P(A_{n+1}) - \P\left(\bigcup_{i=1}^n (A_{n+1} \cap A_i) \right) \] Por la hipótesis de inducción, la fórmula inclusión-exclusión se mantiene para cada unión de\( n \) eventos a la derecha. Aplicar la fórmula y simplificar da la fórmula de inclusión-exclusión para\( n + 1 \) eventos.
Comprobante por contabilidad
Esta es la versión general del mismo argumento que usamos anteriormente para 3 eventos. \( \bigcup_{i \in I} A_i \)es la unión de los eventos disjuntos de la forma\( \left(\bigcap_{i \in K} A_i\right) \cap \left(\bigcap_{i \in K^c} A_i\right)\) donde\( K \) es un subconjunto no vacío del conjunto de índices\( I \). En la fórmula de inclusión-exclusión, el evento correspondiente a un dado\( K \) se mide en\( \P\left(\bigcap_{j \in J} A_j\right) \) para cada no vacío\( J \subseteq K \). Supongamos que\( \#(K) = k \). Contabilizando los signos positivos y negativos, la medición neta es\( \sum_{j=1}^k (-1)^{j-1} \binom{k}{j} = 1 \).
Aquí está el resultado complementario para la probabilidad de una intersección en términos de las probabilidades de las diversas uniones:
La fórmula general de inclusión-exclusión para la probabilidad de una intersección. \[\P\left( \bigcap_{i \in I} A_i \right) = \sum_{k = 1}^n (-1)^{k - 1} \sum_{J \subseteq I, \; \#(J) = k} \P\left( \bigcup_{j \in J} A_j \right)\]
No vale la pena recordar en detalle las fórmulas generales de inclusión-exclusión, sino solo en patrón. Para la probabilidad de una unión, comenzamos con la suma de las probabilidades de los eventos, luego restamos las probabilidades de todas las intersecciones emparejadas, luego sumamos las probabilidades de las intersecciones de tercer orden, y así sucesivamente, alternando signos, hasta llegar a la probabilidad de la intersección de todas las los eventos.
Las desigualdades generales de Bonferroni (para una unión) establecen que si se trunca suma a la derecha en la fórmula general de inclusión-exclusión, entonces la suma truncada es un límite superior o un límite inferior para la probabilidad de la izquierda, dependiendo de si el último término tiene un signo positivo o negativo. Aquí está el resultado declarado explícitamente:
Supongamos que\( m \in \{1, 2, \ldots, n - 1\} \). Entonces
- \(\P\left( \bigcup_{i \in I} A_i \right) \le \sum_{k = 1}^m (-1)^{k - 1} \sum_{J \subseteq I, \; \#(J) = k} \P\left( \bigcap_{j \in J} A_j \right)\)si\( m \) es impar.
- \(\P\left( \bigcup_{i \in I} A_i \right) \ge \sum_{k = 1}^m (-1)^{k - 1} \sum_{J \subseteq I, \; \#(J) = k} \P\left( \bigcap_{j \in J} A_j \right)\)si\( m \) es evento.
Prueba
Let\( P_k = \sum_{J \subseteq I, \; \#(J) = k} \P\left( \bigcap_{j \in J} A_j \right) \), el valor absoluto del término\( k \) th en la fórmula inclusión-exclusión. El resultado sigue ya que la fórmula de inclusión-exclusión es una serie alterna, y\( P_k \) está disminuyendo en\( k \).
Se pueden construir pruebas más elegantes de la fórmula de inclusión-exclusión y las desigualdades Bonferroni utilizando el valor esperado.
Tenga en cuenta que existe un término de probabilidad en las fórmulas de inclusión-exclusión para cada subconjunto no vacío\( J \) del conjunto de índices\( I \), ya sea con un signo positivo o negativo, y por lo tanto existen\( 2^n - 1 \) dichos términos. Estas probabilidades son suficientes para calcular la probabilidad de cualquier evento que pueda construirse a partir de los eventos dados, no solo de la unión o de la intersección.
La probabilidad de cualquier evento que se pueda construir a partir de\( \{A_i: i \in I\} \) puede calcularse a partir de cualquiera de las siguientes colecciones de\( 2^n - 1 \) probabilidades:
- \( \P\left(\bigcap_{j \in J} A_j\right) \)donde\( J \) es un subconjunto no vacío de\( I \).
- \( \P\left(\bigcup_{j \in J} A_j\right) \)donde\( J \) es un subconjunto no vacío de\( I \).
Obrar
Si regresas y miras tus pruebas de las reglas de probabilidad anteriores, verás que se mantienen para cualquier medida finita\(\mu\), no solo probabilidad. El único cambio es que el número 1 es reemplazado por\(\mu(S)\). En particular, la regla de inclusión-exclusión es tan importante en la combinatoria (el estudio de la medida de conteo) como en la probabilidad.
Ejemplos y Aplicaciones
Reglas de Probabilidad
Supongamos que\(A\) y\(B\) son eventos en un experimento con\(\P(A) = \frac{1}{3}\),\(\P(B) = \frac{1}{4}\),\(\P(A \cap B) = \frac{1}{10}\). Expresa cada uno de los siguientes eventos en el lenguaje del experimento y encuentra su probabilidad:
- \(A \setminus B\)
- \(A \cup B\)
- \(A^c \cup B^c\)
- \(A^c \cap B^c\)
- \(A \cup B^c\)
Contestar
- \(A\)ocurre pero no\(B\). \(\frac{7}{30}\)
- \(A\)u\(B\) ocurre. \(\frac{29}{60}\)
- Uno de los eventos no ocurre. \(\frac{9}{10}\)
- Ninguno de los eventos ocurre. \(\frac{31}{60}\)
- O\(A\) ocurre o\(B\) no ocurre. \(\frac{17}{20}\)
Supongamos que\(A\)\(B\),, y\(C\) son eventos en un experimento con\(\P(A) = 0.3\)\(\P(B) = 0.2\),,\(\P(C) = 0.4\),\(\P(A \cap B) = 0.04\),\(\P(A \cap C) = 0.1\),\(\P(B \cap C) = 0.1\),\(\P(A \cap B \cap C) = 0.01\). Exprese cada uno de los siguientes eventos en notación de conjuntos y encuentre su probabilidad:
- Al menos uno de los tres eventos ocurre.
- Ninguno de los tres eventos ocurre.
- Exactamente uno de los tres eventos ocurre.
- Exactamente dos de los tres eventos ocurren.
Contestar
- \(\P(A \cup B \cup C) = 0.67\)
- \(\P[(A \cup B \cup C)^c] = 0.37\)
- \(\P[(A \cap B^c \cap C^c) \cup (A^c \cap B \cap C^c) \cup (A^c \cap B^c \cap C)] = 0.45\)
- \(\P[(A \cap B \cap C^c) \cup (A \cap B^c \cap C) \cup (A^c \cap B \cap C)] = 0.21\)
Supongamos que\(A\) y\(B\) son eventos en un experimento con\(\P(A \setminus B) = \frac{1}{6}\),\(\P(B \setminus A) = \frac{1}{4}\), y\(\P(A \cap B) = \frac{1}{12}\). Encuentra la probabilidad de cada uno de los siguientes eventos:
- \(A\)
- \(B\)
- \(A \cup B\)
- \(A^c \cup B^c\)
- \(A^c \cap B^c\)
Contestar
- \(\frac{1}{4}\)
- \(\frac{1}{3}\)
- \(\frac{1}{2}\)
- \(\frac{11}{12}\)
- \(\frac{1}{2}\)
Supongamos que\(A\) y\(B\) son eventos en un experimento con\(\P(A) = \frac{2}{5}\),\(\P(A \cup B) = \frac{7}{10}\), y\(\P(A \cap B) = \frac{1}{6}\). Encuentra la probabilidad de cada uno de los siguientes eventos:
- \(B\)
- \(A \setminus B\)
- \(B \setminus A\)
- \(A^c \cup B^c\)
- \(A^c \cap B^c\)
Contestar
- \(\frac{7}{15}\)
- \(\frac{7}{30}\)
- \(\frac{3}{10}\)
- \(\frac{5}{6}\)
- \(\frac{3}{10}\)
Supongamos que\(A\)\(B\),, y\(C\) son eventos en un experimento con\(\P(A) = \frac{1}{3}\),\(\P(B) = \frac{1}{4}\),\(\P(C) = \frac{1}{5}\).
- Utilice la desigualdad de Boole para encontrar un límite superior para\(\P(A \cup B \cup C)\).
- Utilice la desigualdad de Bonferronis para encontrar un límite inferior para\(\P(A \cap B \cap C)\).
Contestar
- \(\frac{47}{60}\)
- \(-\frac{83}{60}\), no servicial.
Abra el experimento de probabilidad simple.
- Tenga en cuenta los 16 eventos que se pueden construir a partir\( A \) y\( B \) usando las operaciones establecidas de unión, intersección y complemento.
- Dado\( \P(A) \),\( \P(B) \), y\( \P(A \cap B) \) en la tabla, utilizar las reglas de probabilidad para verificar las probabilidades de los demás eventos.
- Ejecutar el experimento 1000 veces y comparar las frecuencias relativas de los eventos con las probabilidades de los eventos.
Supongamos que\(A\)\(B\),, y\(C\) son eventos en un experimento aleatorio con\( \P(A) = 1/4 \)\( \P(B) = 1/3 \),\( \P(C) = 1/6 \),\( \P(A \cap B) = 1/18 \),\( \P(A \cap C) = 1/16 \),\( \P(B \cap C) = 1/12 \), y\( \P(A \cap B \cap C) = 1/24 \). Encuentra las probabilidades de los distintos sindicatos:
- \( A \cup B \)
- \( A \cup C \)
- \( B \cup C \)
- \( A \cup B \cup C \)
Contestar
- \( 19/36 \)
- \( 17/48 \)
- \( 5/12 \)
- \( 85/144 \)
Supongamos que\(A\)\(B\),, y\(C \) son eventos en un experimento aleatorio con\( \P(A) = 1/4 \)\( \P(B) = 1/4 \),\( \P(C) = 5/16 \),\( \P(A \cup B) = 7/16 \),\( \P(A \cup C) = 23/48 \),\( \P(B \cup C) = 11/24 \), y\( \P(A \cup B \cup C) = 7/12 \). Encuentra las probabilidades de las distintas intersecciones:
- \( A \cap B \)
- \( A \cap C \)
- \( B \cap C \)
- \( A \cap B \cap C \)
Contestar
- \( 1/16 \)
- \( 1/12 \)
- \( 5/48 \)
- \( 1/48 \)
Supongamos que\(A\)\(B\),, y\(C\) son eventos en un experimento aleatorio. Dar explícitamente todas las desigualdades Bonferroni para\( \P(A \cup B \cup C) \)
Prueba
- \( \P(A \cup B \cup C) \le \P(A) + \P(B) + \P(C) \)
- \( \P(A \cup B \cup C) \ge \P(A) + \P(B) + \P(C) - \P(A \cap B) - \P(A \cap C) - \P(B \cap C) \)
- \( \P(A \cup B \cup C) = \P(A) + \P(B) + \P(C) - \P(A \cap B) - \P(A \cap C) - \P(B \cap C) + \P(A \cap B \cap C)\)
Monedas
Considera el experimento aleatorio de lanzar una moneda\(n\) veces y registrar la secuencia de partituras\(\bs{X} = (X_1, X_2, \ldots, X_n)\) (donde 1 denota cabezas y 0 denota colas). Este experimento es un ejemplo genérico de ensayos de\(n\) Bernoulli, llamado así por Jacob Bernoulli. Tenga en cuenta que el conjunto de resultados es\(S = \{0, 1\}^n\), el conjunto de cadenas de bits de longitud\(n\). Si la moneda es justa, entonces presumiblemente, por el significado mismo de la palabra, no tenemos ninguna razón para preferir un punto en\(S\) lugar de otro. Así, como suposición de modelación, parece razonable dar\(S\) la distribución uniforme de probabilidad en la que todos los resultados son igualmente probables.
Supongamos que una moneda justa se lanza 3 veces y se registra la secuencia de puntuaciones de monedas. Que\(A\) sea el evento de que la primera moneda sea cabezas y\(B\) el evento de que haya exactamente 2 cabezas. Dé cada uno de los siguientes eventos en forma de lista y luego calcule la probabilidad del evento:
- \(A\)
- \(B\)
- \(A \cap B\)
- \(A \cup B\)
- \(A^c \cup B^c\)
- \(A^c \cap B^c\)
- \(A \cup B^c\)
Contestar
- \(\{100, 101, 110, 111\}\),\(\frac{1}{2}\)
- \(\{110, 101, 011\}\),\(\frac{3}{8}\)
- \(\{110, 101\}\),\(\frac{1}{4}\)
- \(\{100, 101, 110, 111, 011\}\),\(\frac{5}{8}\)
- \(\{000, 001, 010, 100, 011, 111\}\),\(\frac{3}{4}\)
- \(\{000, 001, 010\}\),\(\frac{3}{8}\)
- \(\{100, 101, 110, 111, 000, 010, 001\}\),\(\frac{7}{8}\)
En el experimento Coin, selecciona 3 monedas. Ejecutar el experimento 1000 veces, actualizándose después de cada ejecución, y computar la probabilidad empírica de cada evento en el ejercicio anterior.
Supongamos que una moneda justa es arrojada 4 veces y se registra la secuencia de puntuaciones. Vamos a\(Y\) denotar el número de cabezas. Dar el evento\(\{Y = k\}\) (como un subconjunto del espacio de muestra) en forma de lista, para cada uno\(k \in \{0, 1, 2, 3, 4\}\), y luego dar la probabilidad del evento.
Contestar
- \(\{Y = 0\} = \{0000\}\),\(\P(Y = 0) = \frac{1}{16}\)
- \(\{Y = 1\} = \{1000, 0100, 0010, 0001\}\),\(\P(Y = 1) = \frac{4}{16}\)
- \(\{Y = 2\} = \{1100, 1010, 1001, 0110, 0101, 0011\}\),\(\P(Y = 2) = \frac{6}{16}\)
- \(\{Y = 3\} = \{1110, 1101, 1011, 0111\}\),\(\P(Y = 3) = \frac{4}{16}\)
- \(\{Y = 4\} = \{1111\}\),\(\P(Y = 4) = \frac{1}{16}\)
Supongamos que una moneda justa es arrojada\(n\) veces y se registra la secuencia de puntuaciones. Vamos a\(Y\) denotar el número de cabezas.
\[\P(Y = k) = \binom{n}{k} \left( \frac{1}{2} \right)^n, \quad k \in \{0, 1, \ldots, n\}\]Prueba
El número de cadenas de bits de longitud\(n\) es\(2^n\), y dado que la moneda es justa, estas son igualmente probables. El número de cadenas de bits de longitud\(n\) con exactamente\(k\) 1's es\(\binom{n}{k}\). De ahí que la probabilidad de que 1 ocurra exactamente\(k\) veces es\(\binom{n}{k} \big/ 2^n\).
La distribución de\(Y\) en el último ejercicio es un caso especial de la distribución binomial. La distribución binomial se estudia con más detalle en el capítulo de Ensayos de Bernoulli.
Dados
Considere el experimento de lanzar\(n\) distintos, dados\(k\) de lados (con caras numeradas del 1 al\(k\)) y registrar la secuencia de partituras\(\bs{X} = (X_1, X_2, \ldots, X_n)\). Podemos registrar el resultado como una secuencia debido a la suposición de que los dados son distintos; se puede pensar en los dados como etiquetados de alguna manera del 1 al\(n\), o tal vez con diferentes colores. El caso especial\(k = 6\) corresponde a dados estándar. En general, señalar que el conjunto de resultados es\(S = \{1, 2, \ldots, k\}^n\). Si los dados son justos, entonces otra vez, por el significado mismo de la palabra, no tenemos ninguna razón para preferir un punto a otro, por lo que como suposición de modelado parece razonable dar\(S\) la distribución uniforme de probabilidad.\( S \)
Supongamos que se lanzan dos dados justos y estándar y se registra la secuencia de puntuaciones. Dejar\(A\) denotar el evento de que la puntuación del primer dado es menor que 3 y\(B\) el evento de que la suma de las puntuaciones de dados es 6. Dar cada uno de los siguientes eventos en forma de lista y luego encontrar la probabilidad del evento.
- \(A\)
- \(B\)
- \(A \cap B\)
- \(A \cup B\)
- \(B \setminus A\)
Contestar
- \(\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)\}\),\(\frac{12}{36}\)
- \(\{(1,5),(5,1),(2,4),(4,2),(3,3)\}\),\(\frac{5}{36}\)
- \(\{(1,5), (2,4)\}\),\(\frac{2}{36}\)
- \(\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(5,1),(4,2),(3,3)\}\),\(\frac{15}{36}\)
- \(\{(5,1), (4,2), (3,3)\}\),\(\frac{3}{36}\)
En el experimento de dados, set\(n = 2\). Ejecutar el experimento 100 veces y calcular la probabilidad empírica de cada evento en el ejercicio anterior.
Considera de nuevo el experimento de dados con dados\(n = 2\) justos. Dejar\( S \) denotar el conjunto de resultados,\(Y\) la suma de las puntuaciones,\(U\) la puntuación mínima y\(V\) la puntuación máxima.
- Expresar\(Y\) como una función\( S \) y dar el conjunto de valores.
- Encuentra\(\P(Y = y)\) para cada uno\(y\) en el conjunto en la parte (a).
- Expresar\(U\) como una función\( S \) y dar el conjunto de valores.
- Encuentra\(\P(U = u)\) para cada uno\(u\) en el conjunto en la parte (c).
- Expresar\(V\) como una función\( S \) y dar el conjunto de valores.
- Encuentra\(\P(V = v)\) para cada uno\(v\) en el conjunto en la parte (e).
- Encuentra el conjunto de valores de\((U, V)\).
- Encuentra\(\P(U = u, V = v)\) para cada uno\((u, v)\) en el conjunto en la parte (g).
Contestar
Tenga en cuenta que\( S = \{1, 2, 3, 4, 5, 6\}^2 \).
- \(Y(x_1, x_2) = x_1 + x_2\)para\( (x_1, x_2) \in S \). El conjunto de valores es\(\{2, 3, \ldots, 12\}\)
-
\(y\) 2 3 4 5 6 7 8 9 10 11 12 \(\P(Y = y)\) \(\frac{1}{36}\) \(\frac{2}{36}\) \(\frac{3}{36}\) \(\frac{4}{36}\) \(\frac{5}{36}\) \(\frac{6}{36}\) \(\frac{5}{36}\) \(\frac{4}{36}\) \(\frac{3}{36}\) \(\frac{2}{36}\) \(\frac{1}{36}\) - \(U(x_1, x_2) = \min\{x_1, x_2\}\)para\( (x_1, x_2) \in S \). El conjunto de valores es\(\{1, 2, 3, 4, 5, 6\}\)
-
\(u\) 1 2 3 4 5 6 \(\P(U = u)\) \(\frac{11}{36}\) \(\frac{9}{36}\) \(\frac{7}{36}\) \(\frac{5}{36}\) \(\frac{3}{36}\) \(\frac{1}{36}\) - \(V(x_1, x_2) = \max\{x_1, x_2\}\)para\( (x_1, x_2) \in S \). El conjunto de valores es\(\{1, 2, 3, 4, 5, 6\}\)
-
\(v\) 1 2 3 4 5 6 \(\P(V = v)\) \(\frac{1}{36}\) \(\frac{3}{36}\) \(\frac{5}{36}\) \(\frac{7}{36}\) \(\frac{9}{36}\) \(\frac{11}{36}\) - \(\left\{(u, v) \in S: u \le v\right\}\)
- \(\P(U = u, V = v) = \begin{cases} \frac{2}{36}, & u \lt v \\ \frac{1}{36}, & u = v \end{cases}\)
En el ejercicio anterior, tenga en cuenta que\((U, V)\) podría servir como vector de resultado para el experimento de rodar dos dados estándar y justos si no nos molestamos en distinguir los dados (para que así podamos registrar primero la puntuación más pequeña y luego la puntuación más grande). Tenga en cuenta que este vector aleatorio no tiene una distribución uniforme. Por otro lado, podríamos haber optado al principio por solo registrar el conjunto desordenado de partituras y, como suposición de modelación, impuso la distribución uniforme sobre el conjunto de resultados correspondiente. Ambos modelos no pueden tener razón, entonces, ¿qué modelo (si alguno) describe los dados reales en el mundo real? Resulta que para los dados reales (justos), la secuencia ordenada de partituras se distribuye uniformemente, por lo que los dados reales se comportan como objetos distintos, ya sea que puedas diferenciarlos o no. En la historia temprana de probabilidad, los apostadores a veces obtuvieron respuestas equivocadas para eventos relacionados con dados porque aplicaron erróneamente la distribución uniforme al conjunto de puntajes desordenados. Es una moraleja importante. Si vamos a imponer la distribución uniforme en un espacio de muestra, debemos asegurarnos de que es el espacio de muestra correcto.
Un par de dados justos y estándar se lanzan repetidamente hasta que la suma de los puntajes sea 5 o 7. Vamos a\(A\) denotar el evento de que la suma de los puntajes en el último tiro es de 5 en lugar de 7. Eventos de este tipo son importantes en el juego de dados.
- Supongamos que grabamos el par de puntajes en cada tirada. Dar el conjunto de resultados\(S\) y expresar\(A\) como un subconjunto de\(S\).
- Calcula la probabilidad de\(A\) en el ajuste de la parte (a).
- Ahora supongamos que solo grabamos el par de anotaciones en el último lanzamiento. Dar el conjunto de resultados\(T\) y expresar\(A\) como un subconjunto de\(T\).
- Calcula la probabilidad de\(A\) en el ajuste de partes (c).
Contestar
Dejar\(D_5 = \{(1,4), (2,3), (3,2), (4,1)\}\)\(D_7 = \{(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\}\),\(D = D_5 \cup D_7\),\(C = \{1, 2, 3, 4, 5, 6\}^2 \setminus D\)
- \(S = D \cup (C \times D) \cup (C^2 \times D) \cup \cdots\),\(A = D_5 \cup (C \times D_5) \cup (C^2 \times D_5) \cup \cdots\)
- \(\frac{2}{5}\)
- \(T = D\),\(A = D_5\)
- \(\frac{2}{5}\)
El problema anterior muestra la importancia de definir adecuadamente el conjunto de resultados. A veces, una elección inteligente de este conjunto (y suposiciones de modelado apropiadas) puede convertir un problema difícil en uno fácil.
Modelos de Muestreo
Recordemos que muchos experimentos aleatorios pueden considerarse como experimentos de muestreo. Para el modelo general de muestreo finito, comenzamos con una población\(D\) con objetos\(m\) (distintos). Seleccionamos una muestra de\(n\) objetos de la población, de manera que el espacio muestral\(S\) sea el conjunto de posibles muestras. Si seleccionamos una muestra al azar entonces el resultado\(\bs{X}\) (la muestra aleatoria) se distribuye uniformemente en\(S\):\[\P(\bs{X} \in A) = \frac{\#(A)}{\#(S)}, \quad A \subseteq S\] Recordemos de la sección de Estructuras Combinatorias que existen cuatro tipos comunes de muestreo de una población finita, con base en los criterios de orden y reemplazo.
- Si el muestreo es con reemplazo y con respecto al orden, entonces el conjunto de muestras es el poder cartesiano\(D^n\). El número de muestras es\(m^n\).
- Si el muestreo es sin reemplazo y con respecto al orden, entonces el conjunto de muestras es el conjunto de todas las permutaciones de tamaño\(n\) de\(D\). El número de muestras es\(m^{(n)} = m (m - 1) \cdots (m - n + 1)\).
- Si el muestreo es sin reemplazo y sin tener en cuenta el orden, entonces el conjunto de muestras es el conjunto de todas las combinaciones (o subconjuntos) de tamaño\(n\) de\(D\). El número de muestras es\(\binom{m}{n} = m^{(n)} / n!\).
- Si el muestreo es con reemplazo y sin importar el orden, entonces el conjunto de muestras es el conjunto de todos los multiconjuntos de tamaño\(n\) de\(D\). El número de muestras es\(\binom{m + n - 1}{n}\).
Si tomamos muestras con reemplazo, el tamaño de la muestra\(n\) puede ser cualquier entero positivo. Si tomamos muestras sin reemplazo, el tamaño de la muestra no puede exceder el tamaño de la población, por lo que debemos tener\(n \in \{1, 2, \ldots, m\}\).
Los experimentos básicos de monedas y dados son ejemplos de muestreo con reemplazo. Si tiramos una moneda justa\(n\) veces y registramos la secuencia de puntuaciones\(\bs{X}\) (donde como de costumbre, 0 denota colas y 1 denota cabezas), entonces\(\bs{X}\) es una muestra aleatoria de tamaño\(n\) elegida con orden y con reemplazo de la población\(\{0, 1\}\). Así,\(\bs{X}\) se distribuye uniformemente sobre\(\{0, 1\}^n\). Si lanzamos dados justos estándar\(n\) (distintos) y registramos la secuencia de puntuaciones, entonces generamos una muestra aleatoria\(\bs{X}\) de tamaño\(n\) con orden y con reemplazo de la población\(\{1, 2, 3, 4, 5, 6\}\). Así,\(\bs{X}\) se distribuye uniformemente sobre\(\{1, 2, 3, 4, 5, 6\}^n\). De un resultado análogo se sostendría para dados justos,\(k\) -lados.
Supongamos que el muestreo es sin reemplazo (el caso más común). Si registramos la muestra ordenada\(\bs{X} = (X_1, X_2, \ldots, X_n)\), entonces la muestra desordenada\(\bs{W} = \{X_1, X_2, \ldots\}\) es una variable aleatoria (es decir, una función de\(\bs{X}\)). Por otro lado, si solo registramos la muestra desordenada\(\bs{W}\) en primer lugar, entonces no podemos recuperar la muestra pedida.
Supongamos que\(\bs{X}\) es una muestra aleatoria de tamaño\(n\) elegida con orden y sin reemplazo de\(D\), de manera que\(\bs{X}\) se distribuye uniformemente en el espacio de permutaciones de tamaño\(n\) desde\(D\). Entonces\(\bs{W}\), la muestra desordenada, se distribuye uniformemente en el espacio de combinaciones de tamaño\(n\) desde\(D\). Así, también\(\bs{W}\) es una muestra aleatoria.
Prueba
Dejar\(\bs{w}\) ser una combinación de tamaño\(n\) de\(D\). Luego hay\(n!\) permutaciones de los elementos en\(\bs{w}\). Si\(A\) denota este conjunto de permutaciones, entonces\(\P(\bs{W} = \bs{w}) = \P(\bs{X} \in A) = n! \big/ m^{(n)} = 1 \big/ \binom{m}{n}\).
El resultado en el último ejercicio no se sostiene si el muestreo es con reemplazo (recordar el ejercicio anterior y la discusión que sigue). Al muestrear con reemplazo, no existe una relación simple entre el número de muestras ordenadas y el número de muestras desordenadas.
Muestreo de una población dicotómica
Supongamos nuevamente que tenemos una población\(D\) con objetos\(m\) (distintos), pero supongamos ahora que cada objeto es uno de dos tipos, ya sea tipo 1 o tipo 0. Se dice que tales poblaciones son dicotómicas. Aquí hay algunos ejemplos específicos:
- La población está compuesta por personas, cada una de ellas masculinas o femeninas.
- La población está formada por votantes, cada uno demócrata o republicano.
- La población consiste en dispositivos, cada uno bien o defectuoso.
- La población consiste en bolas, cada una roja o verde.
Supongamos que la población\(D\) tiene objetos\(r\) tipo 1 y por lo tanto\(m - r\) escribe 0 objetos. Por supuesto, debemos tener\(r \in \{0, 1, \ldots, m\}\). Ahora supongamos que seleccionamos una muestra de tamaño\(n\) al azar de la población. Tenga en cuenta que este modelo tiene tres parámetros: el tamaño de la población\(m\), el número de objetos tipo 1 en la población\(r\) y el tamaño de la muestra\(n\). Dejar\(Y\) denotar el número de objetos tipo 1 en la muestra.
Si el muestreo es sin reemplazo entonces\[\P(Y = y) = \frac{\binom{r}{y} \binom{m - r}{n - y}}{\binom{m}{n}}, \quad y \in \{0, 1, \ldots, n\}\]
Prueba
Recordemos que la muestra desordenada se distribuye uniformemente sobre el conjunto de combinaciones de tamaño\(n\) elegidas de la población. Hay\(\binom{m}{n}\) tales muestras. Por el principio de multiplicación, el número de muestras con exactamente\(y\) tipo 1 objetos y\(n - y\) tipo 0 objetos es\(\binom{r}{y} \binom{m - r}{n - y}\).
En el ejercicio anterior, la variable aleatoria\(Y\) tiene la distribución hipergeométrica con parámetros\(m\),\(r\), y\(n\). La distribución hipergeométrica se estudia con más detalle en el capítulo sobre Modelos de Muestreo Findite.
Si el muestreo es con reemplazo entonces\[\P(Y = y) = \binom{n}{y} \frac{r^y (m - r)^{n-y}}{m^n} = \binom{n}{y} \left( \frac{r}{m}\right)^y \left( 1 - \frac{r}{m} \right)^{n - y}, \quad y \in \{0, 1, \ldots, n\}\]
Prueba
Recordemos que la muestra ordenada se distribuye uniformemente sobre el conjunto\(D^n\) y hay\(m^n\) elementos en este conjunto. Para contar el número de muestras con exactamente los objetos\(y\) tipo 1, utilizamos un procedimiento de tres pasos: primero, seleccionar las coordenadas para los objetos tipo 1; hay\(\binom{n}{y}\) opciones. A continuación, seleccione los objetos\(y\) tipo 1 para estas coordenadas; hay\(r^y\) opciones. Finalmente seleccione los objetos\(n - y\) tipo 0 para las coordenadas restantes de la muestra; hay\((m - r)^{n - y}\) opciones. El resultado ahora se desprende del principio de multiplicación.
En el último ejercicio, la variable aleatoria\(Y\) tiene la distribución binomial con parámetros\(n\) y\(p = \frac{r}{m}\). La distribución binomial se estudia con más detalle en el capítulo de Ensayos de Bernoulli.
Supongamos que un grupo de votantes está formado por 40 demócratas y 30 republicanos. Se elige al azar una muestra de 10 votantes. Encuentra la probabilidad de que la muestra contenga al menos 4 demócratas y al menos 4 republicanos, cada uno de los siguientes casos:
- El muestreo es sin reemplazo.
- El muestreo es con reemplazo.
Contestar
- \(\frac{1\,391\,351\,589}{2\,176\,695\,188} \approx 0.6382\)
- \(\frac{24\,509\,952}{40\,353\,607} \approx 0.6074\)
Busque otras situaciones de muestreo especializadas en los ejercicios a continuación.
Modelos Urna
Dibujar bolas de una urna es una metáfora estándar en probabilidad para el muestreo de una población finita.
Considera una urna con 30 bolas; 10 son rojas y 20 son verdes. Se elige una muestra de 5 bolas al azar, sin reemplazo. Dejar\(Y\) denotar el número de bolas rojas en la muestra. Calcular explícitamente\(\P(Y = y)\) para cada uno\(y \in \{0, 1, 2, 3, 4, 5\}\).
responder
| \(y\) | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| \(\P(Y = y)\) | \(\frac{2584}{23751}\) | \(\frac{8075}{23751}\) | \(\frac{8550}{23751}\) | \(\frac{3800}{23751}\) | \(\frac{700}{23751/}\) | \(\frac{42}{23751}\) |
En la simulación del experimento de bola y urna, seleccione 30 bolas con 10 rojas y 20 verdes, tamaño de muestra 5 y muestreo sin reemplazo. Ejecuta el experimento 1000 veces y compara las probabilidades empíricas con las probabilidades verdaderas que calculaste en el ejercicio anterior.
Considera nuevamente una urna con 30 bolas; 10 son rojas y 20 son verdes. Se elige una muestra de 5 bolas al azar, con reemplazo. Dejar\(Y\) denotar el número de bolas rojas en la muestra. Calcular explícitamente\(\P(Y = y)\) para cada uno\(y \in \{0, 1, 2, 3, 4, 5\}\).
Contestar
| \(y\) | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| \(\P(Y = y)\) | \(\frac{32}{243}\) | \(\frac{80}{243}\) | \(\frac{80}{243}\) | \(\frac{40}{243}\) | \(\frac{10}{243}\) | \(\frac{1}{243}\) |
En la simulación del experimento de bola y urna, seleccione 30 bolas con 10 rojas y 20 verdes, tamaño de muestra 5 y muestreo con reemplazo. Ejecuta el experimento 1000 veces y compara las probabilidades empíricas con las probabilidades verdaderas que calculaste en el ejercicio anterior.
Una urna contiene 15 bolas: 6 son rojas, 5 son verdes y 4 son azules. Se eligen tres bolas al azar, sin reemplazo.
- Encuentra la probabilidad de que las bolas elegidas sean todas del mismo color.
- Encuentra la probabilidad de que las bolas elegidas sean todas de diferentes colores.
Contestar
- \(\frac{34}{455}\)
- \(\frac{120}{455}\)
Supongamos nuevamente que una urna contiene 15 bolas: 6 son rojas, 5 son verdes y 4 son azules. Se eligen tres bolas al azar, con reemplazo.
- Encuentra la probabilidad de que las bolas elegidas sean todas del mismo color.
- Encuentra la probabilidad de que las bolas elegidas sean todas de diferentes colores.
Contestar
- \(\frac{405}{3375}\)
- \(\frac{720}{3375}\)
Tarjetas
Recordemos que una baraja de cartas estándar puede ser modelada por el conjunto de productos\[D = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, j, q, k\} \times \{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\}\] donde la primera coordenada codifica la denominación o tipo (as, 2—10, jota, reina, rey) y donde la segunda coordenada codifica el palo (palos, diamantes, corazones, espadas). A veces representamos una carta como una cuerda en lugar de una pareja ordenada (por ejemplo,\(q \heartsuit\) para la reina de corazones).
Los juegos de cartas implican elegir una muestra aleatoria sin reemplazo de la baraja\(D\), que juega el papel de la población. Así, el experimento básico de cartas consiste en repartir\(n\) cartas de un mazo estándar sin reemplazo; en este contexto especial, la muestra de cartas a menudo se conoce como una mano. Al igual que en el modelo de muestreo general, si registramos la mano ordenada\(\bs{X} = (X_1, X_2, \ldots, X_n)\), entonces la mano desordenada\(\bs{W} = \{X_1, X_2, \ldots, X_n\}\) es una variable aleatoria (es decir, una función de\(\bs{X}\)). Por otro lado, si acabamos de registrar la mano desordenada\(\bs{W}\) en primer lugar, entonces no podemos recuperar la mano ordenada. Por último, recordemos que\(n = 5\) es el experimento del póker y\(n = 13\) es el experimento del puente. El juego de póquer se trata con más detalle en el capítulo de Juegos de azar. Por cierto, se necesitan alrededor de 7 barajadas de riffle estándar para aleatorizar una baraja de cartas.
Supongamos que se reparten 2 cartas de una baraja bien barajada y se registra la secuencia de cartas. Para\(i \in \{1, 2\}\), vamos a\(H_i\) denotar el evento de que la tarjeta\(i\) es un corazón. Encuentra la probabilidad de cada uno de los siguientes eventos.
- \(H_1\)
- \(H_1 \cap H_2\)
- \(H_2 \setminus H_1\)
- \(H_2\)
- \(H_1 \setminus H_2\)
- \(H_1 \cup H_2\)
Contestar
- \(\frac{1}{4}\)
- \(\frac{1}{17}\)
- \(\frac{13}{68}\)
- \(\frac{1}{4}\)
- \(\frac{13}{68}\)
- \(\frac{15}{34}\)
Piensa en los resultados del ejercicio anterior, y supongamos que seguimos repartir cartas. Tenga en cuenta que al calcular la probabilidad de\(H_i\), podría reducir conceptualmente el experimento a repartir una sola carta. Tenga en cuenta también que las probabilidades no dependen del orden en que se reparten las cartas. Por ejemplo, la probabilidad de que un evento involucre las cartas 1ª, 2ª y 3ª es la misma que la probabilidad de que el evento correspondiente involucre las cartas 25, 17 y 40. Técnicamente, las tarjetas son intercambiables. Aquí hay otra forma de pensar en este concepto: Supongamos que las cartas se reparten sobre una mesa en algún patrón, pero no se le permite ver el proceso. Entonces ningún experimento que puedas idear te dará ninguna información sobre el orden en el que se repartieron las cartas.
En el experimento de cartas, set\(n = 2\). Ejecutar el experimento 100 veces y calcular la probabilidad empírica de cada evento en el ejercicio anterior
En el experimento de poker, encuentra la probabilidad de cada uno de los siguientes eventos:
- La mano es una casa llena (3 tarjetas de un tipo y 2 tarjetas de otro tipo).
- La mano tiene cuatro de un tipo (4 cartas de un tipo y 1 de otro tipo).
- Las cartas están todas en el mismo palo (por lo tanto, la mano está a ras o a ras recta).
Contestar
- \(\frac{3744}{2\,598\,960} \approx 0.001441\)
- \(\frac{624}{2\,598\,960} \approx 0.000240\)
- \(\frac{5148}{2\,598\,960} \approx 0.001981\)
Ejecuta el experimento de poker 10000 veces, actualizando cada 10 carreras. Calcular la probabilidad empírica de cada evento en el problema anterior.
Encuentra la probabilidad de que una mano de puente no contenga tarjetas de honor, es decir, ni cartas de denominación 10, jota, reina, rey o as. Tal mano se llama Yarborough, en honor al segundo conde de Yarborough.
Contestar
\(\frac{347\,373\,600}{635\,013\,559\,600} \approx 0.000547\)
Encuentra la probabilidad de que una mano de puente contenga
- Exactamente 4 corazones.
- Exactamente 4 corazones y 3 espadas.
- Exactamente 4 corazones, 3 picas y 2 palos.
Contestar
- \(\frac{151\,519\,319\,380}{635\,013\,559\,600} \approx 0.2386\)
- \(\frac{47\,079\,732\,700}{635\,013\,559\,600} \approx 0.0741\)
- \(\frac{11\,404\,407\,300}{635\,013\,559\,600} \approx 0.0179\)
Se dice que una mano de cartas que no contiene cartas en un palo en particular es nula en ese palo. Utilice la regla de inclusión-exclusión para encontrar la probabilidad de cada uno de los siguientes eventos:
- Una mano de póquer es nula en al menos un palo.
- Una mano de puente es nula en al menos un palo.
Contestar
- \(\frac{1\,913\,496}{2\,598\,960} \approx 0.7363\)
- \(\frac{32\,427\,298\,180}{635\,013\,559\,600} \approx 0.051\)
Cumpleaños
El siguiente problema se conoce como el problema del cumpleaños, y es famoso porque los resultados son bastante sorprendentes al principio.
Supongamos que\(n\) las personas son seleccionadas y se registran sus cumpleaños (ignoraremos los años bisiestos). Dejar\(A\) denotar el evento de que los cumpleaños son distintos, de modo que ese\(A^c\) es el evento de que hay al menos una duplicación en los cumpleaños.
- Definir un espacio muestral apropiado y una medida de probabilidad. Exponga las suposiciones que está haciendo.
- Encuentra\(P(A)\) y\(\P(A^c)\) en términos del parámetro\(n\).
- Computar explícitamente\(P(A)\) y\(P(A^c)\) para\(n \in \{10, 20, 30, 40, 50\}\)
Contestar
- El conjunto de resultados es\(S = D^n\) donde\(D\) está el conjunto de días del año. Suponemos que los resultados son igualmente probables, por lo que\(S\) tiene la distribución uniforme.
- \(\#(A) = 365^{(n)}\), así\(\P(A) = 365^{(n)} / 365^n\) y\(\P(A^c) = 1 - 365^{(n)} / 365^n\)
-
\(n\) \(\P(A)\) \(\P(A^c)\) 10 0.883 0.117 20 0.589 0.411 30 0.294 0.706 40 0.109 0.891 50 0.006 0.994
El pequeño valor de\(\P(A)\) para tamaños de muestra relativamente pequeños\(n\) es llamativo, pero se debe matemáticamente al hecho de que\(365^n\) crece mucho más rápido que a\(365^{(n)}\) medida que\(n\) aumenta. El problema del cumpleaños se trata con más generalidad en el capítulo sobre Modelos de Muestreo Finito.
Supongamos que se seleccionan 4 personas y se registran sus meses de nacimiento. Asumiendo una distribución uniforme apropiada, encuentra la probabilidad de que los meses sean distintos.
Contestar
\(\frac{11880}{20736} \approx 0.573\)
Distribuciones Uniformes Continua
Recordemos que en el experimento de monedas de Buffon, una moneda con radio\(r \le \frac{1}{2}\) es arrojada aleatoriamente
sobre un piso con baldosas cuadradas de longitud lateral 1, y se registran las coordenadas\((X, Y)\) del centro de la moneda, relativas a los ejes a través del centro del cuadrado en el que aterriza la moneda (con los ejes paralelo a los lados de la plaza, por supuesto). Dejar\(A\) denotar el evento de que la moneda no toque los lados de la plaza.
- Definir\(S\) matemáticamente el conjunto de resultados y bosquejar\(S\).
- Argumentan que\((X, Y)\) se distribuye uniformemente en\(S\).
- Expresar\(A\) en términos de las variables de resultado\((X, Y)\) y boceto\(A\).
- Encuentra\(\P(A)\).
- Encuentra\(\P(A^c)\).
Contestar
- \(S = \left[-\frac{1}{2}, \frac{1}{2}\right]^2\)
- Dado que la moneda se lanza al
azar
, no se\(S\) debe preferir ninguna región de sobre ninguna otra. - \(\left\{r - \frac{1}{2} \lt X \lt \frac{1}{2} - r, r - \frac{1}{2} \lt Y \lt \frac{1}{2} - r\right\}\)
- \(\P(A) = (1 - 2 \, r)^2\)
- \(\P(A^c) = 1 - (1 - 2 \, r)^2\)
En el experimento de monedas de Buffon, set\(r = 0.2\). Ejecutar el experimento 100 veces y calcular la probabilidad empírica de cada evento en el ejercicio anterior.
\((X, Y)\)Se elige un punto al azar en la región circular\(S \subset \R^2\) del radio 1, centrado en el origen. Vamos a\(A\) denotar el evento de que el punto está en la región cuadrada inscrita centrada en el origen, con lados paralelos a los ejes de coordenadas, y vamos a\(B\) denotar el evento de que el punto está en el cuadrado inscrito con vértices\((\pm 1, 0)\),\((0, \pm 1)\). Esboce cada uno de los siguientes eventos como un subconjunto de\(S\), y encuentre la probabilidad del evento.
- \(A\)
- \(B\)
- \(A \cap B^c\)
- \(B \cap A^c\)
- \(A \cap B\)
- \(A \cup B\)
Contestar
- \(2 / \pi\)
- \(2 / \pi\)
- \((6 - 4 \sqrt{2}) \big/ \pi\)
- \((6 - 4 \sqrt{2}) \big/ \pi\)
- \(4(\sqrt{2} - 1) \big/ \pi\)
- \(4(2 - \sqrt{2}) \big/ \pi\)
Supongamos que\((X, Y)\) se elige un punto al azar en la región circular\(S \subseteq \R^2\) del radio 12, centrado en el origen. Dejar\(R\) denotar la distancia desde el origen hasta el punto. Esboce cada uno de los siguientes eventos como un subconjunto de\(S\), y calcule la probabilidad del evento. ¿Se distribuye\(R\) uniformemente en el intervalo\([0, 12]\)?
- \(\{R \le 3\}\)
- \(\{3 \lt R \le 6\}\)
- \(\{6 \lt R \le 9\}\)
- \(\{9 \lt R\le 12\}\)
Contestar
No, no\(R\) se distribuye uniformemente en\([0, 12]\).
- \(\frac{1}{16}\)
- \(\frac{3}{16}\)
- \(\frac{5}{16}\)
- \(\frac{7}{16}\)
En el experimento de probabilidad simple, los puntos se generan de acuerdo con la distribución uniforme en un rectángulo. Mueva y cambie el tamaño de los eventos\( A \)\( B \) y anote cómo cambian las probabilidades de los diversos eventos. Cree cada una de las siguientes configuraciones. En cada caso, ejecute el experimento 1000 veces y compare las frecuencias relativas de los eventos con las probabilidades de los eventos.
- \( A \)y\( B \) en posición general
- \( A \)y\( B \) disjuntos
- \( A \subseteq B \)
- \( B \subseteq A \)
Genética
Por favor refiérase a la discusión de genética en la sección de experimentos aleatorios si necesita revisar algunas de las definiciones de esta subsección.
Recordemos primero que el tipo de sangre ABO en humanos está determinado por tres alelos:\(a\),\(b\), y\(o\). Además,\(a\)\(b\) son codominantes y\(o\) recesivos. Supongamos que la distribución de probabilidad para el conjunto de genotipos sanguíneos en una determinada población se da en la siguiente tabla:
| Genotipo | \(aa\) | \(ab\) | \(ao\) | \(bb\) | \(bo\) | \(oo\) |
|---|---|---|---|---|---|---|
| Probabilidad | 0.050 | 0.038 | 0.310 | 0.007 | 0.116 | 0.479 |
Se elige al azar a una persona de la población. Dejar\(A\),\(B\),\(AB\), y\(O\) ser los eventos que la persona es tipo\(A\), tipo\(B\)\(AB\), tipo y tipo\(O\) respectivamente. \(H\)Sea el evento de que la persona sea homocigótica y\(D\) el evento de que la persona tenga un\(o\) alelo. Encuentra la probabilidad de los siguientes eventos:
- \(A\)
- \(B\)
- \(AB\)
- \(O\)
- \(H\)
- \(D\)
- \(H \cup D\)
- \(D^c\)
Contestar
- 0.360
- 0.123
- 0.038
- 0.479
- 0.536
- 0.905
- 0.962
- 0.095
Supongamos a continuación que el color de la vaina en cierto tipo de planta de guisante está determinado por un gen con dos alelos:\(g\) para el verde y\(y\) para el amarillo, y que\(g\) es dominante.
\(G\)Sea el evento de que una planta infantil tenga vainas verdes. Encuentra\(\P(G)\) en cada uno de los siguientes casos:
- Al menos uno de los padres es tipo\(gg\).
- Ambos padres son tipo\(yy\).
- Ambos padres son tipo\(gy\).
- Uno de los padres es tipo\(yy\) y el otro es tipo\(gy\).
Contestar
- \(1\)
- \(0\)
- \(\frac{3}{4}\)
- \(\frac{1}{2}\)
A continuación, considere un trastorno hereditario vinculado al sexo en humanos (como el daltonismo o la hemofilia). Dejar\(h\) denotar el alelo sano y\(d\) el alelo defectuoso para el gen vinculado al trastorno. Recordemos que\(d\) es recesivo para las mujeres.
\(B\)Sea el evento de que un hijo tenga el trastorno,\(C\) el evento de que una hija sea portadora sana, y\(D\) el evento de que una hija tenga la enfermedad. Encuentre\(\P(B)\),\(\P(C)\) y\(\P(D)\) en cada uno de los siguientes casos:
- La madre y el padre son normales.
- La madre es una portadora sana y el padre es normal.
- La madre es normal y el padre tiene el trastorno.
- La madre es una portadora sana y el padre tiene el trastorno.
- La madre tiene el trastorno y el padre es normal.
- Tanto la madre como el padre tienen el trastorno.
Contestar
- \(0\),\(0\),\(0\)
- \(1/2\), 0,\(1/2\)
- \(0\),\(1/2\),\(0\)
- \(1/2\),\(1/2\),\(1/2\)
- \(1\),\(1/2\),\(0\)
- \(1\),\(0\),\(1\)
De este ejercicio, señalar que la transmisión del trastorno a una hija sólo puede ocurrir si la madre es al menos portadora y el padre tiene el trastorno. En poblaciones grandes ordinarias, esta es una intersección inusual de eventos y, por lo tanto, los trastornos hereditarios vinculados al sexo suelen ser mucho menos comunes en mujeres que en hombres. En resumen, las mujeres están protegidas por el cromosoma X extra.
Emisiones radiactivas
Supongamos que\(T\) denota el tiempo entre emisiones (en milisegundos) para un determinado tipo de material radiactivo, y que\(T\) tiene la siguiente distribución de probabilidad, definida para medible\(A \subseteq [0, \infty)\) por\[\P(T \in A) = \int_A e^{-t} \, dt\]
- Demuestre que esto realmente define una distribución de probabilidad.
- Encuentra\(\P(T \gt 3)\).
- Encuentra\(\P(2 \lt T \lt 4)\).
Contestar
- Tenga en cuenta que\( \int_0^\infty e^{-t} \, dt = 1 \)
- \(e^{-3}\)
- \(e^{-2} - e^{-4}\)
Supongamos que\(N\) denota el número de emisiones en un intervalo de un milisegundo para un determinado tipo de material radiactivo, y que\(N\) tiene la siguiente distribución de probabilidad:\[\P(N \in A) = \sum_{n \in A} \frac{e^{-1}}{n!}, \quad A \subseteq \N\]
- Demuestre que esto realmente define una distribución de probabilidad.
- Encuentra\(\P(N \ge 3)\).
- Encuentra\(\P(2 \le N \le 4)\).
Contestar
- Tenga en cuenta que\( \sum_{n=0}^\infty \frac{e^{-1}}{n!} = 1 \)
- \(1 - \frac{5}{2} e^{-1}\)
- \(\frac{17}{24} e^{-1}\)
La distribución de probabilidad que gobierna el tiempo entre emisiones es un caso especial de la distribución exponencial, mientras que la distribución de probabilidad que gobierna el número de emisiones es un caso especial de la distribución de Poisson, llamada así por Simeón Poisson. La distribución exponencial y la distribución de Poisson se estudian con más detalle en el capítulo sobre el proceso de Poisson.
Coincidencia
Supongamos que a una secretaria de mente ausente prepara 4 cartas y sobres coincidentes para enviar a 4 personas diferentes, pero luego mete las letras en los sobres al azar. Encuentra la probabilidad del evento de\(A\) que al menos una letra esté en el sobre adecuado.
Solución
Obsérvese primero que el conjunto de resultados se\( S \) puede tomar como el conjunto de permutaciones de\(\{1, 2, 3, 4\}\). For\(\bs{x} \in S\),\(x_i\) es el número del sobre que contiene la letra\(i\) th. Claramente se\(S\) debe dar la distribución uniforme de probabilidad. A continuación, tenga en cuenta que\(A = A_1 \cup A_2 \cup A_3 \cup A_4\) dónde\(A_i\) está el evento de que la letra\(i\) th se inserta en el\(i\) th sobre. El uso de la regla de inclusión-exclusión da\(\P(A) = \frac{5}{8}\).
Este ejercicio es un ejemplo del problema de emparejamiento, originalmente formulado y estudiado por Pierre Remond Montmort. Un análisis completo del problema de emparejamiento se da en el capítulo sobre Modelos de Muestreo Finito.
En la simulación del experimento de emparejamiento seleccionar\(n = 4\). Ejecute el experimento 1000 veces y calcule la frecuencia relativa del evento en el que se produzca al menos una coincidencia.
Ejercicios de Análisis de Datos
Para el conjunto de datos de M&M, vamos a\(R\) denotar el evento de que una bolsa tenga al menos 10 caramelos rojos,\(T\) el evento de que una bolsa tenga al menos 57 caramelos en total, y\(W\) el evento de que una bolsa pese al menos 50 gramos. Encuentra la probabilidad empírica de los siguientes eventos:
- \(R\)
- \(T\)
- \(W\)
- \(R \cap T\)
- \(T \setminus W\)
Contestar
- \(\frac{13}{30}\)
- \(\frac{19}{30}\)
- \(\frac{9}{30}\)
- \(\frac{9}{30}\)
- \(\frac{11}{30}\)
Para los datos de cigarra, vamos a\(W\) denotar el evento de que una cigarra pesa al menos 0.20 gramos,\(F\) el evento de que una cigarra es hembra, y\(T\) el evento de que una cigarra es tipo tredecula. Encuentra la probabilidad empírica de cada uno de los siguientes:
- \(W\)
- \(F\)
- \(T\)
- \(W \cap F\)
- \(F \cup T \cup W\)
Contestar
- \(\frac{37}{104}\)
- \(\frac{59}{104}\)
- \(\frac{44}{104}\)
- \(\frac{34}{104}\)
- \(\frac{85}{104}\)


