3.2: Distribuciones continuas
- Page ID
- 151647
En la sección anterior, consideramos distribuciones discretas. En esta sección, estudiamos un tipo complementario de distribución. Como de costumbre, si eres un nuevo estudiante de probabilidad, es posible que quieras saltarte los detalles técnicos.
Teoría Básica
Definiciones y Propiedades Básicas
Como es habitual, nuestro punto de partida es un experimento aleatorio modelado por un espacio de probabilidad\((S, \mathscr S, \P)\). Entonces, para revisar,\(S\) es el conjunto de resultados,\(\mathscr S\) la recolección de eventos, y\(\P\) la medida de probabilidad en el espacio muestral\((S, \mathscr S)\). Utilizamos los términos medida de probabilidad y distribución de probabilidad como sinónimos en este texto. Además, dado que usamos una definición general de variable aleatoria, cada medida de probabilidad puede pensarse como la distribución de probabilidad de una variable aleatoria, por lo que siempre podemos tomar este punto de vista si queremos. De hecho, la mayoría de las medidas de probabilidad tienen naturalmente variables aleatorias asociadas a ellas.
En esta sección, suponemos que\(S \subseteq \R^n\) para algunos\(n \in \N_+\).
Detalles
Técnicamente,\( S \) es un subconjunto medible de\( \R^n \) y\( \mathscr S \) es el\( \sigma \) -álgebra subconjuntos medibles de\( S \). Típicamente en aplicaciones,\( S \) se define por un número finito de desigualdades que involucran la función elemental.
Aquí está nuestra primera definición fundamental.
La medida de probabilidad\( \P \) es continua si es\(\P(\{x\}) = 0\) para todos\(x \in S\).
El hecho de que a cada punto se le asigne probabilidad 0 puede parecer imposible o paradójico al principio, pero pronto veremos analogías muy familiares.
Si\(\P\) es una distribución continua entonces\(\P(C) = 0\) para cada contable\(C \subseteq S\).
Prueba
Dado que\(C\) es contable, se deduce del axioma de la aditividad de probabilidad que
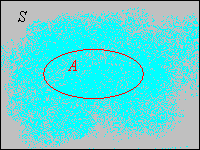
\[ \P(C) = \sum_{x \in C} \P(\{x\}) = 0 \]Así, las distribuciones continuas están en completo contraste con las distribuciones discretas, para lo cual toda la masa de probabilidad se concentra en los puntos en un conjunto discreto. Para una distribución continua, la masa de probabilidad se extiende continuamente\(S\) en algún sentido. En la imagen de abajo, el sombreado azul claro pretende sugerir una distribución continua de la probabilidad.

Típicamente,\( S \) es una región de\( \R^n \) definida por desigualdades que involucran funciones elementales, por ejemplo, un intervalo en\(\R\), una región circular en\(\R^2\), y una región cónica en\(\R^3\). Supongamos que\(\P\) es una medida de probabilidad continua en\(S\). El hecho de que cada punto en\( S \) tenga probabilidad 0 es conceptualmente el mismo que el hecho de que un intervalo de\(\R\) puede tener longitud positiva aunque esté compuesto por puntos cada uno de los cuales tiene 0 longitud. De igual manera, una región de\(\R^2\) puede tener área positiva aunque esté compuesta por puntos (o curvas) cada uno de los cuales tiene área 0. En el caso unidimensional, se utilizan distribuciones continuas para modelar variables aleatorias que toman valores en intervalos de\( \R \), variables que pueden, en principio, medirse con cualquier grado de precisión. Tales variables abundan en aplicaciones e incluyen
- longitud, área, volumen y distancia
- tiempo
- masa y peso
- carga, voltaje y corriente
- resistencia, capacitancia e inductancia
- velocidad y aceleración
- energía, fuerza y trabajo
Por lo general, una distribución continua suele ser descrita por cierto tipo de función.
Supongamos nuevamente que\(\P\) es una distribución continua en\(S\). Una función\(f: S \to [0, \infty)\) es una función de densidad de probabilidad para\(\P\) if\[\P(A) = \int_A f(x) \, dx, \quad A \in \mathscr S\]
Detalles
Técnicamente,\( f \) debe ser medible y es una función de densidad de probabilidad\( \P \) con respecto a la medida de Lebesgue, la medida estándar en\( \R^n \). Además, la integral es la integral de Lebesgue, pero la integral ordinaria de Riemann de cálculo es suficiente para los conjuntos que ocurren en aplicaciones típicas.
Entonces, la distribución de probabilidad\(\P\) está completamente determinada por la función de densidad de probabilidad\(f\). Como caso especial, tenga en cuenta que\(\int_S f(x) \, dx = \P(S) = 1\). Por el contrario, una función no negativa on\(S\) con esta propiedad define una medida de probabilidad.
Una función\(f: S \to [0, \infty)\) que satisface\(\int_S f(x) \, dx = 1\) es una función de densidad de probabilidad en\(S\) y luego\(\P\) se define de la siguiente manera es una medida de probabilidad continua en\(S\):\[\P(A) = \int_A f(x) \, dx, \quad A \in \mathscr S\]
Prueba
Tenga en cuenta que siempre podemos extender\(f\) a una función de densidad de probabilidad en un subconjunto de\(\R^n\) que contiene\(S\), o a todos\(\R^n\), definiendo\(f(x) = 0\) for\(x \notin S\). Esta extensión a veces simplifica la notación. Dicho de otra manera, podemos ser un poco descuidados sobre el conjunto de valores
de la variable aleatoria. Entonces por ejemplo si\(a, \, b \in \R\) con\(a \lt b\) y\(X\) tiene una distribución continua en el intervalo\([a, b]\), entonces también podríamos decir que\(X\) tiene una distribución continua en\((a, b)\) o\([a, b)\), o\((a, b]\).
Los puntos\( x \in S \) que maximizan la función de densidad de probabilidad\( f \) son importantes, al igual que en el caso discreto.
Supongamos que\(\P\) es una distribución continua\(S\) con función de densidad de probabilidad\(f\). Un elemento\(x \in S\) que maximiza\(f\) es un modo de distribución.
Si solo hay un modo, a veces se usa como medida del centro de la distribución.
Probablemente haya notado que las funciones de densidad de probabilidad para distribuciones continuas son análogas a las funciones de densidad de probabilidad para distribuciones discretas, con integrales que reemplazan sumas. Sin embargo, existen diferencias esenciales. Primero, cada distribución discreta tiene una función de densidad de probabilidad única\(f\) dada por\(f(x) = \P(\{x\})\) for\(x \in S\). Para una distribución continua, no se garantiza la existencia de una función de densidad de probabilidad. La sección avanzada sobre funciones de continuidad absoluta y densidad tiene varios ejemplos de distribución continua que no tienen funciones de densidad, y da condiciones que son necesarias y suficientes para la existencia de una función de densidad de probabilidad. Aunque\(f\) exista una función de densidad de probabilidad, nunca es única. Tenga en cuenta que los valores de\(f\) en un conjunto finito (o incluso contablemente infinito) de puntos podrían cambiarse a otros valores no negativos y la nueva función seguiría siendo una función de densidad de probabilidad para la misma distribución. El hecho crítico es que sólo las integrales de\(f\) son importantes. Segundo, los valores del PDF\(f\) para una distribución discreta son probabilidades, y en particular\(f(x) \le 1\) para\(x \in S\). Para una distribución continua los valores no son probabilidades y de hecho es posible que\(f(x) \gt 1\) para algunos o incluso para todos\(x \in S\). Además,\(f\) puede ser sin límites en\(S\). En la interpretación típica del cálculo,\(f(x)\) realmente es densidad de probabilidad en\(x\). Es decir,\(f(x) \, dx\) es aproximadamente la probabilidad de una pequeña
región de tamaño\(dx\) aproximadamente\(x\).
Construcción de funciones de densidad de probabilidad
Al igual que en el caso discreto, una función no negativa en a menudo se\( S \) puede escalar para producir una función de densidad de probabilidad producir.
Supongamos eso\(g: S \to [0, \infty)\) y let\[c = \int_S g(x) \, dx\]\(0 \lt c \lt \infty\) If entonces\(f\) definido por\(f(x) = \frac{1}{c} g(x)\) for\(x \in S\) define una función de densidad de probabilidad para una distribución continua en\(S\).
Prueba
Técnicamente, la función\( g \) es medible. Aparte de tecnicismos, la prueba es trivial. Claramente\( f(x) \ge 0 \) para\( x \in S \) y\[ \int_S f(x) \, dx = \frac{1}{c} \int_S g(x) \, dx = \frac{c}{c} = 1 \]
Tenga en cuenta nuevamente que\(f\) es solo una versión a escala de\(g\). Por lo que este resultado se puede utilizar para construir funciones de densidad de probabilidad con las propiedades deseadas (dominio, forma, simetría, etc.). A la constante\(c\) se le llama a veces la constante normalizadora de\(g\).
Densidades Condicionales
Supongamos ahora que\(X\) es una variable aleatoria definida en un espacio de probabilidad\( (\Omega, \mathscr F, \P) \) y que\( X \) tiene una distribución continua encendida\(S\). Una función de densidad de probabilidad para\(X\) se basa en la medida de probabilidad subyacente en el espacio muestral\((\Omega, \mathscr F)\). Esta medida podría ser una medida de probabilidad condicional, condicionada a un evento dado\(E \in \mathscr F\) con\(\P(E) \gt 0\). Suponiendo que existe la función de densidad de probabilidad condicional, la notación habitual es\[f(x \mid E), \quad x \in S\] Note, sin embargo, que a excepción de la notación, no hay conceptos nuevos involucrados. La propiedad definitoria es\[\int_A f(x \mid E) \, dx = \P(X \in A \mid E), \quad A \in \mathscr S\] y todos los resultados que se mantienen para funciones de densidad de probabilidad en general se mantienen para funciones de densidad de probabilidad condicional. El evento\( E \) podría ser un evento descrito en términos de la\( X \) propia variable aleatoria:
Supongamos que\( X \) tiene una distribución continua\(S\) con función de densidad de probabilidad\( f \) y que\(B \in \mathscr S\) con\(\P(X \in B) \gt 0\). La función de densidad de probabilidad condicional de\(X\) dado\(X \in B\) es la función on\(B\) dada por\[f(x \mid X \in B) = \frac{f(x)}{\P(X \in B)}, \quad x \in B \]
Prueba
Para\(A \in \mathscr S\) con\(A \subseteq B\),\[ \int_A \frac{f(x)}{\P(X \in B)} \, dx = \frac{1}{\P(X \in B)} \int_A f(x) \, dx = \frac{\P(X \in A)}{\P(X \in B)} = \P(X \in A \mid X \in B) \]
Por supuesto,\( \P(X \in B) = \int_B f(x) \, dx \) y por lo tanto es la constante normaliziang para la restricción de\( f \) a\( B \), como en (8)
Ejemplos y Aplicaciones
Como siempre, prueba los problemas tú mismo antes de mirar las respuestas.
La distribución exponencial
Dejar\(f\) ser la función definida por\(f(t) = r e^{-r t}\) for\(t \in [0, \infty) \), donde\(r \in (0, \infty)\) es un parámetro.
- Mostrar que\( f \) es una función de densidad de probabilidad.
- Dibujar un boceto cuidadoso de la gráfica de\( f \), y exponer las características cualitativas importantes.
Prueba
- Tenga en cuenta que\( f(t) \gt 0 \) para\( t \ge 0 \). También\( \int_0^\infty e^{-r t} \, dt = \frac{1}{r} \) lo\( f \) es un PDF.
- \( f \)es decreciente y cóncava hacia arriba por lo que el modo es 0. \( f(x) \to 0 \)como\( x \to \infty \).
La distribución definida por la función de densidad de probabilidad en el ejercicio anterior se denomina distribución exponencial con parámetro de tasa\(r\). Esta distribución se utiliza frecuentemente para modelar tiempos aleatorios, bajo ciertos supuestos. Específicamente, en el modelo de Poisson de puntos aleatorios en el tiempo, los tiempos entre llegadas sucesivas tienen distribuciones exponenciales independientes, y el parámetro\(r\) es la tasa promedio de llegadas. La distribución exponencial se estudia en detalle en el capítulo sobre Procesos de Poisson.
La vida útil\(T\) de un determinado dispositivo (en unidades de 1000 horas) tiene la distribución exponencial con parámetro\(r = \frac{1}{2}\). Encuentra
- \(\P(T \gt 2)\)
- \(\P(T \gt 3 \mid T \gt 1)\)
Contestar
- \(e^{-1} \approx 0.3679\)
- \(e^{-1} \approx 0.3679\)
En el experimento gamma, configurado\( n =1 \) para obtener la distribución exponencial. Varíe el parámetro de tasa\( r \) y anote la forma de la función de densidad de probabilidad. Para varios valores de\(r\), ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
Un ángulo aleatorio
En el problema de Bertrand, un cierto ángulo aleatorio\(\Theta\) tiene la función de densidad de probabilidad\(f\) dada por\(f(\theta) = \sin \theta\) for\(\theta \in \left[0, \frac{\pi}{2}\right]\).
- Mostrar que\(f\) es una función de densidad de probabilidad.
- Dibuje un boceto cuidadoso de la gráfica\(f\) y exponga las características cualitativas importantes.
- Encontrar\(\P\left(\Theta \lt \frac{\pi}{4}\right)\).
Contestar
- Tenga en cuenta que\( \sin \theta \ge 0 \) para\( 0 \le \theta \le \frac{\pi}{2} \) y\( \int_0^{\pi/2} \sin \theta \, d\theta = 1 \).
- \( f \)está aumentando y cóncavo hacia abajo por lo que el modo es\(\frac{\pi}{2}\).
- \(1 - \frac{1}{\sqrt{2}} \approx 0.2929\)
El problema de Bertand lleva el nombre de Joseph Louis Bertrand y se estudia con más detalle en el capítulo sobre Modelos Geométricos.
En el experimento de Bertrand, seleccione el modelo con distancia uniforme. Ejecutar la simulación 1000 veces y calcular la probabilidad empírica del evento\(\left\{\Theta \lt \frac{\pi}{4}\right\}\). Comparar con la probabilidad verdadera en el ejercicio anterior.
Distribuciones Gamma
Dejar\(g_n\) ser la función definida por\(g_n(t) = e^{-t} \frac{t^n}{n!}\) para\(t \in [0, \infty)\) donde\(n \in \N\) es un parámetro.
- Mostrar que\(g_n\) es una función de densidad de probabilidad para cada uno\(n \in \N\).
- Dibujar un boceto cuidadoso de la gráfica de\(g_n\), y exponer las características cualitativas importantes.
Prueba
- Tenga en cuenta que\( g_n(t) \ge 0 \) para\( t \ge 0 \). También,\( g_0 \) es la función de densidad de probabilidad de la distribución exponencial con el parámetro 1. Para\( n \in \N_+ \), integración por partes con\( u = t^n / n! \) y\( dv = e^{-t} dt \) da\( \int_0^\infty g_n(t) \, dt = \int_0^\infty g_{n-1}(t) \, dt \). De ahí que se deduce por inducción que\( g_n \) es un PDF para cada uno\( n \in \N_+ \).
- \( g_0 \)es decreciente y cóncavo hacia abajo, con modo\( t = 0 \). Para\( n \gt 0 \),\( g_n \) aumenta y luego disminuye, con modo\( t = n \). \( g_1 \)es cóncava hacia abajo y luego hacia arriba, con punto de inflexión en\( t = 2 \). Porque\( n \gt 1 \),\( g_n \) es cóncava hacia arriba, luego hacia abajo, luego hacia arriba nuevamente, con puntos de inflexión en\( n \pm \sqrt{n} \). Para todos\( n \in \N \),\( g_n(t) \to 0 \) como\( t \to \infty \).
Curiosamente, mostramos en la última sección sobre distribuciones discretas, que\(f_t(n) = g_n(t)\) es una función de densidad de probabilidad\(\N\) para cada una\(t \ge 0\) (es la distribución de Poisson con parámetro\(t\)). La distribución definida por la función de densidad de probabilidad\(g_n\) pertenece a la familia de distribuciones Erlang, llamada así por Agner Erlang;\( n + 1 \) se conoce como el parámetro shape. La distribución de Erlang se estudia con más detalle en el capítulo sobre el Proceso de Poisson. A su vez, la distribución Erlang pertenece a la familia más general de distribuciones gamma. La distribución gamma se estudia con más detalle en el capítulo sobre Distribuciones Especiales.
En el experimento gamma, mantenga el parámetro de tasa por defecto\(r = 1\). Variar el parámetro shape y anotar la forma y ubicación de la función de densidad de probabilidad. Para varios valores del parámetro shape, ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
Supongamos que la vida útil de un dispositivo\(T\) (en unidades de 1000 horas) tiene la distribución gamma anterior con\(n = 2\). Encuentra cada uno de los siguientes:
- \(\P(T \gt 3)\).
- \( \P(T \le 2) \)
- \( \P(1 \le T \le 4) \)
Contestar
- \(\frac{17}{2} e^{-3} \approx 0.4232\)
- \( 1 - 5 e^{-2} \approx 0.3233 \)
- \( \frac{5}{2} e^{-1} - 13 e^{-4} \approx 0.6816 \)
Distribuciones Beta
Dejar\(f\) ser la función definida por\(f(x) = 6 x (1 - x)\) for\(x \in [0, 1]\).
- Mostrar que\( f \) es una función de densidad de probabilidad.
- Dibujar un boceto cuidadoso de la gráfica de\(f\), y exponer las características cualitativas importantes.
Contestar
- Tenga en cuenta que\( f(x) \ge 0 \) para\( x \in [0, 1] \). También\( \int_0^1 x (1 - x) \, dx = \frac{1}{6} \), también lo\( f \) es un PDF
- \( f \)aumenta y luego disminuye, con el modo en\(x = \frac{1}{2} \). \( f \)es cóncavo hacia abajo. \( f \)es simétrico sobre\( x = \frac{1}{2} \) (de hecho, la gráfica es una parábola).
Dejar\(f\) ser la función definida por\(f(x) = 12 x^2 (1 - x)\) for\(x \in [0, 1]\).
- Mostrar que\( f \) es una función de densidad de probabilidad.
- Dibuja un boceto cuidadoso de la gráfica\(f\), y exponer las características cualitativas importantes.
Contestar
- Tenga en cuenta que\( f(x) \ge 0 \) para\( 0 \le x \le 1 \). También\( \int_0^1 x^2 (1 - x) \, dx = \frac{1}{12} \), también lo\( f \) es un PDF.
- \( f \)aumenta y luego disminuye, con el modo en\(x = \frac{2}{3}\). \( f \)es cóncava hacia arriba y luego hacia abajo, con punto de inflexión en\(x = \frac{1}{3}\).
Las distribuciones definidas en los dos últimos ejercicios son ejemplos de distribuciones beta. Estas distribuciones son ampliamente utilizadas para modelar proporciones y probabilidades aleatorias, y cantidades físicas que toman valores en intervalos acotados (que, después de un cambio de unidades, pueden tomarse como\( [0, 1] \)). Las distribuciones beta se estudian en detalle en el capítulo sobre Distribuciones especiales.
En el simulador de distribución especial, seleccione la distribución beta. Para los siguientes valores de parámetros, anote la forma de la función de densidad de probabilidad. Ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
Supongamos que\( P \) es una proporción aleatoria. Encuentra\( \P\left(\frac{1}{4} \le P \le \frac{3}{4}\right) \) en cada uno de los siguientes casos:
- \( P \)tiene la primera distribución beta anterior.
- \( P \)tiene la segunda distribución beta anterior.
Contestar
- \(\frac{11}{16}\)
- \(\frac{11}{16}\)
Dejar\( f \) ser la función definida por\[f(x) = \frac{1}{\pi \sqrt{x (1 - x)}}, \quad x \in (0, 1)\]
- Mostrar que\( f \) es una función de densidad de probabilidad.
- Dibujar un boceto cuidadoso de la gráfica de\(f\), y exponer las características cualitativas importantes.
Contestar
- Tenga en cuenta que\( f(x) \gt 0 \) para\( 0 \lt x \lt 1 \). Usando la\( u = \sqrt{x} \) sustitución dada\[ \int_0^1 \frac{1}{\sqrt{x (1 - x)}} \, dx = \int_0^1 \frac{2}{\sqrt{1 - u^2}} \, du = 2 \arcsin u \biggm|_0^1 = \pi \] Así\( f \) es un PDF.
- \( f \)es simétrico sobre\( x = \frac{1}{2} \). \( f \)disminuye y luego aumenta, con mínimo en\( x = \frac{1}{2} \). \( f(x) \to \infty \)como\( x \downarrow 0 \) y como\( x \uparrow 1 \) así la distribución no tiene modo. \( f \)es cóncavo hacia arriba.
La distribución definida en el último ejercicio también es miembro de la familia beta de distribuciones. Pero también se le conoce como la distribución (estándar) del arcoseno, debido a la función arcoseno que surge en la prueba de que\( f \) es una función de densidad de probabilidad. La distribución del arcoseno tiene aplicaciones a un proceso aleatorio muy importante conocido como movimiento browniano, llamado así por el botánico escocés Robert Brown. Las distribuciones de Arcsine se estudian en mayor generalidad en el capítulo sobre Distribuciones Especiales.
En el simulador de distribución especial, seleccione la distribución de arcoseno (continua) y mantenga los valores de los parámetros predeterminados. Ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
Supongamos que\( X_t \) representa el cambio en el precio de una acción en el momento\( t \), relativo al valor en un tiempo de referencia inicial 0. Tratamos\( t \) como una variable continua medida en semanas. Let\( T = \max\left\{t \in [0, 1]: X_t = 0\right\} \), la última vez durante la primera semana que el precio de las acciones se mantuvo sin cambios sobre su valor inicial. Bajo ciertas condiciones ideales,\( T \) tendrá la distribución del arcoseno. Encuentra cada uno de los siguientes:
- \( \P\left(T \lt \frac{1}{4}\right)\)
- \( \P\left(T \ge \frac{1}{2}\right) \)
- \( \P\left(T \le \frac{3}{4}\right) \)
Contestar
- \( \frac{1}{3} \)
- \( \frac{1}{2} \)
- \( \frac{2}{3} \)
Abra el experimento de movimiento browniano y seleccione la última variable cero. Ejecuta el experimento en modo de un solo paso varias veces. El proceso aleatorio que observas modela el precio de la acción en el ejercicio anterior. Ahora ejecuta el experimento 1000 veces y calcula la probabilidad empírica de cada evento en el ejercicio anterior.
La distribución de Pareto
Dejar\(g\) ser la función definida por\(g(x) = 1 /x^b\) for\(x \in [1, \infty)\), donde\(b \in (0, \infty)\) es un parámetro.
- Dibuja un boceto cuidadoso de la gráfica\(g\), y exponer las características cualitativas importantes.
- Encuentra los valores de\( b \) para los cuales existe una función de densidad de probabilidad\( f \) (8) proporcional a\(g\). Identificar el modo.
Contestar
- \( g \)es decreciente y cóncava hacia arriba, con\( g(x) \to 0 \) as\( x \to \infty \).
- Tenga en cuenta que si\( b \ne 1 \)\[\int_1^\infty x^{-b} \, dx = \frac{x^{1 - b}}{1 - b} \biggm|_1^\infty = \begin{cases} \infty, & 0 \lt b \lt 1 \\ \frac{1}{b - 1}, & 1 \lt b \lt \infty \end{cases} \] Cuando\( b = 1 \) tenemos\( \int_1^\infty x^{-1} \, dx = \ln x \biggm|_1^\infty = \infty \). Así, cuando\( 0 \lt b \le 1 \), no hay PDF proporcional a\( g \). Cuando\( b \gt 1 \), el PDF proporcional a\( g \) es\( f(x) = \frac{b - 1}{x^b} \) para\( x \in [1, \infty) \). El modo es 1.
Tenga en cuenta que las características cualitativas de\( g \) son las mismas, independientemente del valor del parámetro\( b \gt 0 \), pero solo cuando se\( b \gt 1 \)\( g \) puede normalizar en una función de densidad de probabilidad. En este caso, la distribución se conoce como la distribución de Pareto, llamada así por Vilfredo Pareto. El parámetro\(a = b - 1\), de modo que\(a \gt 0\), se conoce como el parámetro shape. Así, la distribución de Pareto con parámetro de forma\(a\) tiene función de densidad de probabilidad\[f(x) = \frac{a}{x^{a+1}}, \quad x \in [1, \infty)\] La distribución de Pareto es ampliamente utilizada para modelar ciertas variables económicas y se estudia en detalle en el capítulo sobre Distribuciones Especiales.
En el simulador de distribución especial, seleccione la distribución de Pareto. Deje el parámetro scale fijo, pero varíe el parámetro shape, y anote la forma de la función de densidad de probabilidad. Para varios valores del parámetro shape, ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
Supongamos que el ingreso\(X\) (en unidades apropiadas) de una persona seleccionada aleatoriamente de una población tiene la distribución de Pareto con parámetro shape\(a = 2\). Encuentra cada uno de los siguientes:
- \(\P(X \gt 2)\)
- \( \P(X \le 4) \)
- \( \P(3 \le X \le 5) \)
Contestar
- \(\frac{1}{4}\)
- \( \frac{15}{16} \)
- \( \frac{16}{225} \)
La distribución de Cauchy
Dejar\( f \) ser la función definida por\[f(x) = \frac{1}{\pi (x^2 + 1)}, \quad x \in \R\]
- Mostrar que\( f \) es una función de densidad de probabilidad.
- Dibuja un boceto cuidadoso de la gráfica\(f\), y exponer las características cualitativas importantes.
Contestar
- Tenga en cuenta que\( f(x) \gt 0 \) para\( x \in \R \). También\[ \int_{-\infty}^\infty \frac{1}{1 + x^2} \, dx = \arctan x \biggm|_{-\infty}^\infty = \pi \] y por lo tanto\( f \) es un PDF.
- \( f \)aumenta y luego disminuye, con modo\(x = 0\). \( f \)es cóncava hacia arriba, luego hacia abajo, luego hacia arriba nuevamente, con puntos de inflexión en\(x = \pm \frac{1}{\sqrt{3}}\). \( f \)es simétrico sobre\( x = 0 \).
La distribución construida en el ejercicio anterior se conoce como la distribución (estándar) de Cauchy, llamada así por Augustin Cauchy También podría llamarse la distribución arcangente, debido a la aparición de la función arcangente en la prueba de que\( f \) es una probabilidad función de densidad. Al respecto, anotar la similitud con la distribución del arcoseno anterior. La distribución de Cauchy se estudia con más generalidad en el capítulo sobre Distribuciones Especiales. Obsérvese también que la distribución de Cauchy se obtiene normalizando la función\(x \mapsto \frac{1}{1 + x^2}\); la gráfica de esta función es conocida como la bruja de Agnesi, en honor a Maria Agnesi.
En el simulador de distribución especial, seleccione la distribución de Cauchy con los valores de parámetros predeterminados. Ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
Una fuente de luz está a 1 metro de distancia de la posición 0 en una pared recta infinita. El ángulo\( \Theta \) que hace el haz de luz con la perpendicular a la pared se elige aleatoriamente del intervalo\( \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \). La posición\( X = \tan(\Theta) \) del haz de luz en la pared tiene la distribución estándar de Cauchy. Encuentra cada uno de los siguientes:
- \( \P(-1 \lt X \lt 1) \).
- \( \P\left(X \ge \frac{1}{\sqrt{3}}\right)\)
- \( \P(X \le \sqrt{3}) \)
Contestar
- \( \frac{1}{2} \)
- \( \frac{1}{3} \)
- \(\frac{2}{3}\)
El experimento de Cauchy (con los valores de los parámetros predeterminados) es una simulación del experimento en el último ejercicio.
- Ejecuta el experimento varias veces en modo de un solo paso.
- Ejecute el experimento 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
- Utilizando los datos de (b), computar la frecuencia relativa de cada evento en el ejercicio anterior, y comparar con la probabilidad verdadera.
La distribución normal estándar
Dejar\(\phi\) ser la función definida por\(\phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-z^2/2}\) for\(z \in \R\).
- Mostrar que\( \phi \) es una función de densidad de probabilidad.
- Dibuja un boceto cuidadoso de la gráfica\(\phi\), y exponer las características cualitativas importantes.
Prueba
- Tenga en cuenta que\( \phi(z) \gt 0 \) para\( z \in \R \). Vamos\(c = \int_{-\infty}^\infty e^{-z^2 / 2} \, dz\). Después\[ c^2 = \int_{-\infty}^\infty e^{-x^2/2} \, dx \int_{-\infty}^\infty e^{-y^2/2} \, dy = \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-(x^2 + y^2) / 2} \, dx \, dy \] Cambiar a coordenadas polares:\(x = r \cos \theta\),\(y = r \sin \theta\) dónde\(r \in [0, \infty)\) y\(\theta \in [0, 2 \pi)\). Entonces\(x^2 + y^2 = r^2\) y\(dx \, dy = r \, dr \, d\theta\). De ahí que\[ c^2 = \int_0^{2 \pi} \int_0^\infty r e^{-r^2 / 2} \, dr \, d\theta \] usando la simple sustitución\(u = r^2\), la integral interna es\(\int_0^\infty e^{-u} du = 1\). Entonces la integral externa es\(\int_0^{2\pi} 1 \, d\theta = 2 \pi\). De ahí\( c = \sqrt{2 \pi} \) y así\( f \) es un PDF.
- Tenga en cuenta que\( \phi \) es simétrico alrededor de 0. \( \phi \)aumenta y luego disminuye, con modo\( z = 0 \). \( \phi \)es cóncava hacia arriba, luego hacia abajo, luego hacia arriba nuevamente, con puntos de inflexión en\(z = \pm 1 \). \( \phi(z) \to 0 \)como\( z \to \infty \) y como\( z \to -\infty \).
La distribución definida en el último ejercicio es la distribución normal estándar, quizás la distribución más importante en probabilidad y estadística. Su importancia proviene en gran parte del teorema del límite central, uno de los teoremas fundamentales en probabilidad. En particular, las distribuciones normales son ampliamente utilizadas para modelar mediciones físicas que están sujetas a pequeños errores aleatorios. La familia de distribuciones normales se estudia en mayor generalidad en el capítulo sobre Distribuciones Especiales.
En el simulador de distribución especial, seleccione la distribución normal y mantenga los valores de los parámetros predeterminados. Ejecute la simulación 1000 veces y compare la función de densidad empírica y la función de densidad de probabilidad.
La función\(z \mapsto e^{-z^2 / 2}\) es un ejemplo notorio de una función integrable que no tiene una antiderivada que pueda expresarse en forma cerrada en términos de otras funciones elementales. (Por eso tuvimos que recurrir al truco de coordenadas polares para mostrar que\(\phi\) es una función de densidad de probabilidad). Por lo que las probabilidades que involucran la distribución normal generalmente se calculan utilizando software matemático o estadístico.
Supongamos que el error\( Z \) en la longitud de una determinada pieza mecanizada (en milímetros) tiene la distribución normal estándar. Utilice software matemático para aproximar cada uno de los siguientes:
- \( \P(-1 \le Z \le 1) \)
- \( \P(Z \gt 2) \)
- \( \P(Z \lt -3) \)
Contestar
- 0.6827
- 0.0228
- 0.0013
La distribución extrema del valor
Dejar\(f\) ser la función definida por\(f(x) = e^{-x} e^{-e^{-x}}\) for\(x \in \R\).
- Mostrar que\(f\) es una función de densidad de probabilidad.
- Dibujar un boceto cuidadoso de la gráfica de\(f\), y exponer las características cualitativas importantes.
- Encontrar\(\P(X \gt 0)\), donde\(X\) tiene función de densidad de probabilidad\(f\).
Contestar
- Tenga en cuenta que\( f(x) \gt 0 \) para\( x \in \R \). Usando la sustitución\( u = e^{-x} \),\[ \int_{-\infty}^\infty e^{-x} e^{-e^{-x}} \, dx = \int_0^\infty e^{-u} \, du = 1 \] (tenga en cuenta que el integrando en la última integral es el PDF exponencial con el parámetro 1.
- \( f \)aumenta y luego disminuye, con modo\(x = 0\). \( f \)es cóncava hacia arriba, luego hacia abajo, luego hacia arriba nuevamente, con puntos de inflexión en\(x = \pm \ln\left[\left(3 + \sqrt{5}\right)\middle/2\right] \). Tenga en cuenta sin embargo que no\( f \) es simétrico alrededor de 0. \( f(x) \to 0 \)como\( x \to \infty \) y como\( x \to -\infty \).
- \(1 - e^{-1} \approx 0.6321\)
La distribución en el último ejercicio es la distribución de valor extremo tipo 1 (estándar), también conocida como la distribución de Gumbel en honor a Emil Gumbel. Las distribuciones de valores extremos se estudian en mayor generalidad en el capítulo sobre Distribuciones Especiales.
En el simulador de distribución especial, seleccione la distribución de valor extremo. Mantenga los valores de los parámetros predeterminados y anote la forma y ubicación de la función de densidad de probabilidad. Ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
La distribución logística
Dejar\( f \) ser la función definida por\[f(x) = \frac{e^x}{(1 + e^x)^2}, \quad x \in \R\]
- Mostrar que\(f\) es una función de densidad de probabilidad.
- Dibuja un boceto cuidadoso de la gráfica\(f\), y exponer las características cualitativas importantes.
- Encontrar\(\P(X \gt 1)\), donde\(X\) tiene función de densidad de probabilidad\(f\).
Contestar
- Tenga en cuenta que\( f(x) \gt 0 \) para\( x \in \R \). La sustitución\( u = e^x \) da\[ \int_{-\infty}^\infty f(x) \, dx = \int_0^\infty \frac{1}{(1 + u)^2} \, du = 1 \]
- \( f \)es simétrico alrededor de 0. \( f \)aumenta y luego disminuye con el modo\(x = 0\). \( f \)es cóncava hacia arriba, luego hacia abajo, luego hacia arriba nuevamente, con puntos de inflexión en\(x = \pm \ln\left(2 + \sqrt{3}\right)\). \( f(x) \to 0 \)como\( x \to \infty \) y como\( x \to -\infty \).
- \(\frac{1}{1 + e} \approx 0.2689\)
La distribución en el último ejercicio es la distribución logística (estándar). Las distribuciones logísticas se estudian en mayor generalidad en el capítulo sobre Distribuciones Especiales.
En el simulador de distribución especial, seleccione la distribución logística. Mantenga los valores de los parámetros predeterminados y anote la forma y ubicación de la función de densidad de probabilidad. Ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
Distribuciones Weibull
Dejar\(f\) ser la función definida por\(f(t) = 2 t e^{-t^2}\) for\( t \in [0, \infty) \).
- Mostrar que\(f\) es una función de densidad de probabilidad.
- Dibuja un boceto cuidadoso de la gráfica\(f\), y exponer las características cualitativas importantes.
Contestar
- Tenga en cuenta que\( f(t) \ge 0 \) para\( t \ge 0 \). La sustitución\( u = t^2 \) da\( \int_0^\infty f(t) \, dt = \int_0^\infty e^{-u} \, du = 1 \).
- \( f \)aumenta y luego disminuye, con modo\(t = 1/\sqrt{2} \). \( f \)es cóncava hacia abajo y luego hacia arriba, con punto de inflexión en\(t = \sqrt{3/2}\). \( f(t) \to 0 \)como\( t \to \infty \).
Dejar\(f\) ser la función definida por\(f(t) = 3 t^2 e^{-t^3}\) for\(t \ge 0\).
- Mostrar que\(f\) es una función de densidad de probabilidad.
- Dibuja un boceto cuidadoso de la gráfica\(f\), y exponer las características cualitativas importantes.
Contestar
- Tenga en cuenta que\( f(t) \ge 0 \) para\( t \ge 0 \). La sustitución\( u = t^3 \) da\[ \int_0^\infty f(t) \, dt = \int_0^\infty e^{-u} \, du = 1 \]
- \( f \)aumenta y luego disminuye, con modo\(t = \left(\frac{2}{3}\right)^{1/3}\). \( f \)es cóncava hacia arriba, luego hacia abajo, luego hacia arriba nuevamente, con puntos de inflexión en\( t = \left(1 \pm \frac{1}{3}\sqrt{7}\right)^{1/3} \). \( f(t) \to 0 \)como\( t \to \infty \).
Las distribuciones en los dos últimos ejercicios son ejemplos de distribuciones de Weibull, nombre para Waloddi Weibull. Las distribuciones Weibull se estudian en mayor generalidad en el capítulo sobre Distribuciones Especiales. A menudo se utilizan para modelar tiempos de falla aleatorios de dispositivos (en unidades apropiadamente escaladas).
En el simulador de distribución especial, seleccione la distribución de Weibull. Para cada uno de los siguientes valores del parámetro shape\(k\), anote la forma y ubicación de la función de densidad de probabilidad. Ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
Supongamos que\( T \) es el tiempo de falla de un dispositivo (en unidades de 1000 horas). Encuentra\( \P\left(T \gt \frac{1}{2}\right) \) en cada uno de los siguientes casos:
- \( T \)tiene la primera distribución de Weibull arriba.
- \( T \)tiene la segunda distribución de Weibull arriba.
Contestar
- \(e^{-1/4} \approx 0.7788\)
- \(e^{-1/8} \approx 0.8825\)
Ejemplos adicionales
Dejar\(f\) ser la función definida por\(f(x) = -\ln x\) for\(x \in (0, 1]\).
- Mostrar que\(f\) es una función de densidad de probabilidad.
- Dibujar un boceto cuidadoso de la gráfica de\(f\), y exponer las características cualitativas importantes.
- Encuentre\(\P\left(\frac{1}{3} \le X \le \frac{1}{2}\right)\) dónde\(X\) tiene la función de densidad de probabilidad en (a).
Contestar
- Tenga en cuenta que\( -\ln x \ge 0 \) para\(0 \lt x \le 1\). Integración por partes con\( u = -\ln x \) y\( dv = dx \) da\[ \int_0^1 -\ln x \, dx = -x \ln x \biggm|_0^1 + \int_0^1 1 \, dx = 1 \]
- \( f \)es decreciente y cóncava hacia arriba, con\( f(x) \to \infty \) as\( x \downarrow 0 \), por lo que no hay modo.
- \(\frac{1}{2} \ln 2 - \frac{1}{3} \ln 3 + \frac{1}{6} \approx 0.147\)
Dejar\(f\) ser la función definida por\(f(x) = 2 e^{-x} (1 - e^{-x})\) for\(x \in [0, \infty)\).
- Mostrar que\( f \) es una función de densidad de probabilidad.
- Dibuja un boceto cuidadoso de la gráfica de\(f\), y dar las características cualitativas importantes.
- Encuentre\(\P(X \ge 1)\) dónde\(X\) tiene la función de densidad de probabilidad en (a).
Contestar
- Tenga en cuenta que\( f(x) \gt 0 \) para\( 0 \lt x \lt \infty. \). También\( \int_0^\infty \left(e^{-x} - e^{-2 x}\right) \, dx = \frac{1}{2} \), también lo\( f \) es un PDF.
- \( f \)aumenta y luego disminuye, con modo\( x = \ln(2) \). \( f \)es cóncava hacia abajo y luego hacia arriba, con un punto de inflexión en\( x = \ln(4) \). \( f(x) \to 0 \)como\( x \to \infty \).
- \(2 e^{-1} - e^{-2} \approx 0.6004 \)
Los siguientes problemas tratan con vectores aleatorios bidimensionales y tridimensionales que tienen distribuciones continuas. La idea de normalizar una función para formar una función de densidad de probabilidad es importante para algunos de los problemas. La relación entre la distribución de un vector y la distribución de sus componentes se discutirá más adelante, en la sección sobre distribuciones conjuntas.
Dejar\(f\) ser la función definida por\(f(x, y) = x + y\) for\(0 \le x \le 1\),\(0 \le y \le 1\).
- Mostrar que\(f\) es una función de densidad de probabilidad, e identificar el modo.
- Encuentre\(\P(Y \ge X)\) dónde\((X, Y)\) tiene la función de densidad de probabilidad en (a).
- Encuentra la densidad condicional de\((X, Y)\) dado\(\left\{X \lt \frac{1}{2}, Y \lt \frac{1}{2}\right\}\).
Contestar
- modo\( (1, 1) \)
- \(\frac{1}{2}\)
- \(f\left(x, y \bigm| X \lt \frac{1}{2}, Y \lt \frac{1}{2}\right) = 8 (x + y)\)para\(0 \lt x \lt \frac{1}{2}\),\(0 \lt y \lt \frac{1}{2}\)
Dejar\(g\) ser la función definida por\(g(x, y) = x + y\) for\(0 \le x \le y \le 1\).
- Encuentra la función de densidad de probabilidad\(f\) que es proporcional a\(g\).
- Encuentre\(\P(Y \ge 2 X)\) dónde\((X, Y)\) tiene la función de densidad de probabilidad en (a).
Contestar
- \(f(x,y) = 2(x + y)\),\(0 \le x \le y \le 1\)
- \(\frac{5}{12}\)
Dejar\(g\) ser la función definida por\(g(x, y) = x^2 y\) for\(0 \le x \le 1\),\(0 \le y \le 1\).
- Encuentra la función de densidad de probabilidad\(f\) que es proporcional a\(g\).
- Encuentre\(\P(Y \ge X)\) dónde\((X, Y)\) tiene la función de densidad de probabilidad en (a).
Contestar
- \(f(x,y) = 6 x^2 y\)para\(0 \le x \le 1\),\(0 \le y \le 1\)
- \(\frac{2}{5}\)
Dejar\(g\) ser la función definida por\(g(x, y) = x^2 y\) for\(0 \le x \le y \le 1\).
- Encuentra la función de densidad de probabilidad\(f\) que es proporcional a\(g\).
- Encuentre\(P(Y \ge 2 X)\) dónde\((X, Y)\) tiene la función de densidad de probabilidad en (a).
Contestar
- \(f(x,y) = 15 x^2 y\)para\(0 \le x \le y \le 1\)
- \(\frac{1}{8}\)
Dejar\(g\) ser la función definida por\(g(x, y, z) = x + 2 y + 3 z\) for\(0 \le x \le 1\),\(0 \le y \le 1\),\(0 \le z \le 1\).
- Encuentra la función de densidad de probabilidad\(f\) que es proporcional a\(g\).
- Encuentre\(\P(X \le Y \le Z)\) dónde\((X, Y, Z)\) tiene la función de densidad de probabilidad en (a).
Contestar
- \(f(x, y, z) = \frac{1}{3}(x + 2 y + 3 z)\)para\(0 \le x \le 1\),\(0 \le y \le 1\),\(0 \le z \le 1\)
- \(\frac{7}{36}\)
Dejar\(g\) ser la función definida por\(g(x, y) = e^{-x} e^{-y}\) for\(0 \le x \le y \lt \infty\).
- Encuentra la función de densidad de probabilidad\(f\) que es proporcional a\( g \).
- Encuentre\(\P(X + Y \lt 1)\) dónde\((X, Y)\) tiene la función de densidad de probabilidad en (a).
Contestar
- \(f(x,y) = 2 e^{-x} e^{-y}\),\(0 \lt x \lt y \lt \infty\)
- \(1 - 2 e^{-1} \approx 0.2642\)
Distribuciones uniformes continuas
Nuestra próxima discusión se centrará en una importante clase de distribuciones continuas que se definen puramente en términos de geometría. Necesitamos una definición preliminar.
Para\(n \in \N_+\), la medida estándar\(\lambda_n\) en\(\R^n\) viene dada por\[\lambda_n(A) = \int_A 1 \, dx, \quad A \subseteq \R^n\] En particular,\(\lambda_1(A)\) es la longitud de\(A \subseteq \R\),\(\lambda_2(A)\) es el área de\(A \subseteq \R^2\), y\(\lambda_3(A)\) es el volumen de\(A \subseteq \R^3\).
Detalles
Técnicamente,\( \lambda_n \) es Lebesgue medida en el\( \sigma \) -álgebra de subconjuntos medibles de\( \R^n \). El nombre es en honor a Henri Lebesgue. La representación anterior en términos de la integral estándar de Riemann de cálculo funciona para los conjuntos que ocurren en aplicaciones típicas. Para lo que resta de esta discusión, asumimos que todos los subconjuntos de los\( \R^n \) que se mencionan son mensurables
Tenga en cuenta que si\(n \gt 1\), la integral anterior es una integral múltiple. Generalmente,\(\lambda_n(A)\) se conoce como el volumen\(n\) -dimensional de\(A \in \subseteq \R^n\).
Supongamos que\(S \subseteq \R^n\) para algunos\( n \in \N_+ \) con\(0 \lt \lambda_n(S) \lt \infty\).
- la función\(f\) definida por\(f(x) = 1 \big/ \lambda_n(S)\) for\(x \in S\) es una función de densidad de probabilidad en\(S\).
- La medida de probabilidad asociada con\( f \) está dada por\(\P(A) = \lambda_n(A) \big/ \lambda_n(S) \) for\(A \subseteq S\), y se conoce como la distribución uniforme en\( S \).
Prueba
La prueba es simple: Claramente\( f(x) \gt 0 \) para\( x \in S \) y\[ \int_A f(x) \, dx = \frac{1}{\lambda_n(S)} \int_A 1 \, dx = \frac{\lambda_n(A)}{\lambda_n(S)}, \quad A \subseteq S \] En particular, cuando\( A = S \) tenemos\( \int_S f(x) \, dx = 1 \).
Tenga en cuenta que la probabilidad asignada a un conjunto\(A \subseteq \R^n\) es proporcional al tamaño de\(A\), medida por\(\lambda_n\). Obsérvese también que tanto en los casos discretos como continuos, la distribución uniforme en un conjunto\(S\) tiene una función de densidad de probabilidad constante encendida\(S\). La distribución uniforme en un conjunto\( S \) gobierna un punto\( X \) elegido al azar
de\( S \), y en el caso continuo, tales distribuciones juegan un papel fundamental en diversos Modelos Geométricos. Las distribuciones uniformes se estudian en mayor generalidad en el capítulo sobre Distribuciones Especiales.
El caso especial más importante es la distribución uniforme en un intervalo\([a, b]\) donde\(a, b \in \R\) y\(a \lt b\). En este caso, la función de densidad de probabilidad es\[f(x) = \frac{1}{b - a}, \quad a \le x \le b\] Esta distribución modela un punto elegido al azar
del intervalo. En particular, la distribución uniforme en\([0, 1]\) se conoce como la distribución uniforme estándar, y es muy importante por su simplicidad y el hecho de que puede transformarse en una variedad de otras distribuciones de probabilidad en\(\R\). Casi todos los lenguajes informáticos cuentan con procedimientos para simular variables independientes y uniformes estándar, las cuales se denominan números aleatorios en este contexto.
Las distribuciones condicionales correspondientes a una distribución uniforme también son uniformes.
Supongamos que\(R \subseteq S \subseteq \R^n\) para algunos\( n \in \N_+ \), y eso\(\lambda_n(R) \gt 0\) y\(\lambda_n(S) \lt \infty\). Si la distribución uniforme\(\P\) está\(S\) encendida, entonces la distribución condicional dada\(R\) es uniforme on\(R\).
Prueba
La prueba es muy sencilla: Por\(A \subseteq R\),
\[ \P(A \mid R) = \frac{\P(A \cap R)}{\P(R)} = \frac{\P(A)}{\P(R)} = \frac{\lambda_n(A) \big/ \lambda_n(S)}{\lambda_n(R) \big/ \lambda_n(S)} = \frac{\lambda_n(A)}{\lambda_n(R)} \]El último teorema tiene implicaciones importantes para las simulaciones. Si podemos simular una variable aleatoria que se distribuye uniformemente en un conjunto, podemos simular una variable aleatoria que se distribuye uniformemente en un subconjunto.
Supongamos otra vez eso\(R \subseteq S \subseteq \R^n\) para algunos\( n \in \N_+ \), y eso\(\lambda_n(R) \gt 0\) y\(\lambda_n(S) \lt \infty\). Supongamos además que\(\bs X = (X_1, X_2, \ldots)\) es una secuencia de variables aleatorias independientes, cada una distribuida uniformemente en\(S\). Vamos\(N = \min\{k \in \N_+: X_k \in R\}\). Entonces
- \(N\)tiene la distribución geométrica en el parámetro\(\N_+\) con éxito\(p = \lambda_n(R) \big/ \lambda_n(S)\).
- \(X_N\)se distribuye uniformemente en\(R\).
Prueba
- Dado que las variables se distribuyen de forma unificada en\(S\),\(\P(X_k \in \R) = \lambda_n(R) / \lambda_n(S)\) para cada una\(k \in \N_+\). Dado que las variables son independientes, cada punto está en\(R\) o no de forma independiente. De ahí\(N\) que el índice del primer punto en caer\(R\), tenga la distribución geométrica encendida\(\N_+\) con probabilidad de éxito\(p = \lambda_n(R) / \lambda_n(S)\). Es decir,\(\P(N = k) = (1 - p)^{k-1} p\) para\(k \in \N_+\).
- Tenga en cuenta que\(p \in (0, 1]\), así\(\P(N \in \N_+) = 1\) y por lo tanto\(X_N\) está bien definido. Sabemos por nuestro trabajo sobre independencia y probabilidad condicional que la distribución de\(X_N\) es la misma que la distribución condicional de\(X\) dado\(X \in R\), que por el teorema anterior, se distribuye uniformemente sobre\(R\).
Supongamos en particular que\(S\) es un producto cartesiano de intervalos\(n\) acotados. Resulta bastante fácil simular una secuencia de variables aleatorias independientes\(\bs X = (X_1, X_2, \ldots)\) cada una de las cuales se distribuye uniformemente en\(S\). Así, el último teorema da un algoritmo para simular una variable aleatoria que se distribuye uniformemente sobre una región de forma irregular\(R \subseteq S\) (suponiendo que tenemos un algoritmo para reconocer cuándo\(x \in \R^n\) cae un punto\(R\)). Este método de simulación se conoce como el método de rechazo, y como veremos en secciones posteriores, es más importante que pueda aparecer primero.
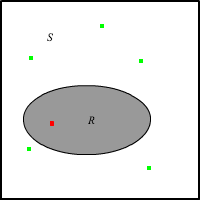
En el experimento de probabilidad simple, los puntos aleatorios se distribuyen uniformemente en la región rectangular\( S \). Mueva y redimensione los eventos\( A \)\( B \) y anote cómo\( B \) cambian las probabilidades de los 16 eventos que se pueden construir a partir de\( A \) los cuales se pueden construir. Ejecutar el experimento 1000 veces y anotar la concordancia entre las frecuencias relativas de los eventos y las probabilidades de los eventos.
Supongamos que\( (X, Y) \) se distribuye uniformemente sobre la región circular de radio 5, centrada en el origen. Podemos pensar en la posición de\( (X, Y) \) un dardo lanzado al azar
a un objetivo. Dejar\( R = \sqrt{X^2 + Y^2} \), la distancia desde el centro a\( (X, Y) \).
- Dar la función de densidad de probabilidad de\( (X, Y) \).
- Encuentra\( \P(n \le R \le n + 1 \) para\( n \in \{0, 1, 2, 3, 4\} \).
Contestar
- \( f(x, y) = \frac{1}{25 \pi} \)para\( \left\{(x, y) \in \R^2: x^2 + y^2 \le 25\right\} \)
- \( \P(n \le R \le n + 1) = \frac{2 n + 1}{25} \)para\( n \in \{0, 1, 2, 3, 4\} \)
Supongamos que\((X, Y, Z)\) se distribuye uniformemente sobre el cubo\(S = [0, 1]^3\). Encuentra\(\P(X \lt Y \lt Z)\) de dos maneras:
- Usando la función de densidad de probabilidad.
- Usando un argumento combinatorio.
Contestar
- \( \P(X \lt Y \lt Z) = \int_0^1 \int_0^z \int_0^y 1 \, dx \, dy \, dz = \frac{1}{6} \)
- Cada uno de los 6 ordenamientos estrictos de\( (X, Y, Z) \) son igualmente probables, por lo que\( \P(X \lt Y \lt Z) = \frac{1}{6} \)
El tiempo\(T\) (en minutos) requerido para realizar un determinado trabajo se distribuye uniformemente a lo largo del intervalo\([15, 60]\).
- Encuentra la probabilidad de que el trabajo requiera más de 30 minutos
- Dado que el trabajo no está terminado después de 30 minutos, encuentre la probabilidad de que el trabajo requiera más de 15 minutos adicionales.
Contestar
- \(\frac{2}{3}\)
- \(\frac{1}{6}\)
Ejercicios de Análisis de Datos
Si\(D\) es un conjunto de datos de una variable\(X\) con una distribución continua, entonces se puede calcular una función de densidad empírica particionando el rango de datos en subconjuntos de tamaño pequeño, y luego calculando la densidad de probabilidad de puntos en cada subconjunto. Las funciones de densidad de probabilidad empírica se estudian con más detalle en el capítulo sobre Muestras Aleatorias.
Para los datos de la cigarra,\(BW\) denota el peso corporal (en gramos), la longitud\(BL\) corporal (en milímetros) y el\(G\) género (0 para la hembra y 1 para el masculino). Construir una función de densidad empírica para cada una de las siguientes y mostrar cada una como un gráfico de barras:
- \(BW\)
- \(BL\)
- \(BW\)dado\(G = 0\)
Contestar
-
BW \((0, 0.1]\) \((0.1, 0.2]\) \((0.2, 0.3]\) \((0.3, 0.4]\) Densidad 0.8654 5.8654 3.0769 0.1923 -
BL \((15, 29]\) \((20, 25]\) \((25, 30]\) \((30, 35]\) Densidad 0.0058 0.1577 0.0346 0.0019 -
BW \((0, 0.1]\) \((0.1, 0.2]\) \((0.2, 0.3]\) \((0.3, 0.4]\) Densidad dada\(G = 0\) 0.3390 4.4068 5.0847 0.1695


