3.4: Distribuciones conjuntas
- Page ID
- 151578
El propósito de esta sección es estudiar cómo se relaciona la distribución de un par de variables aleatorias con las distribuciones de las variables individualmente. Si eres un nuevo estudiante de probabilidad es posible que quieras saltarte los detalles técnicos.
Teoría Básica
Distribuciones Articuladas y Marginales
Como es habitual, comenzamos con un experimento aleatorio modelado por un espacio de probabilidad\((\Omega, \mathscr F, \P)\). Entonces, para revisar,\(\Omega\) es el conjunto de resultados,\(\mathscr F\) es la colección de eventos, y\(\P\) es la medida de probabilidad en el espacio muestral\((\Omega, \mathscr F)\). Supongamos ahora que\(X\) y\(Y\) son variables aleatorias para el experimento, y que\(X\) toma valores in\(S\) while\(Y\) toma valores adentro\(T\). Podemos pensar en una variable aleatoria tomando valores en el conjunto de productos\(S \times T\).\((X, Y)\) El propósito de esta sección es estudiar cómo la distribución de\((X, Y)\) se relaciona con las distribuciones de\(X\) e\(Y\) individualmente.
Recordemos que
- La distribución de\((X, Y)\) es la medida de probabilidad\(S \times T\) dada por\(\P\left[(X, Y) \in C\right] \) for\(C \subseteq S \times T\).
- La distribución de\(X\) es la medida de probabilidad\(S\) dada por\(\P(X \in A) \) for\( A \subseteq S \).
- La distribución de\( Y \) es la medida de probabilidad\(T\) dada por\(\P(Y \in B) \) for\( B \subseteq T \).
En este contexto, la distribución de\((X, Y)\) se denomina distribución conjunta, mientras que las distribuciones de\(X\) y de se\(Y\) denominan distribuciones marginales.
Detalles
Los conjuntos\(S\) y\(T\) vienen con\(\sigma\) -álgebras de subconjuntos admisibles\(\mathscr S\) y\(\mathscr T\), respectivamente, así como la colección de eventos\(\mathscr F\) es un\(\sigma\) -álgebra. Al conjunto de productos cartesianos\(S \times T\) se le da el producto\(\sigma\) -álgebra\(\mathscr S \otimes \mathscr T\) generado por los productos\(A \times B\) donde\(A \in \mathscr S\) y\(B \in \mathscr T\). Las variables aleatorias\(X\) y\(Y\) son medibles, lo que asegura que también\((X, Y)\) es una variable aleatoria (es decir, medible). Además, la distribución de\((X, Y)\) está determinada de manera única por las probabilidades de la forma\(\P[(X, Y) \in A \times B] = \P(X \in A, Y \in B)\) donde\(A \in \mathscr S\) y\(B \in \mathscr T\). Como es habitual los espacios\( (S, \mathscr S) \) y\( (T, \mathscr T) \) cada uno caen dentro de las dos clases que hemos estudiado en los apartados anteriores:
- Discreto: el conjunto es contable y el\( \sigma \) -álgebra consiste en todos los subconjuntos.
- Euclidiana: el conjunto es un subconjunto medible de\( \R^n \) para algunos\( n \in \N_+ \) y el\( \sigma \) álgebra consiste en los subconjuntos medibles.
El primer punto simple pero muy importante, es que las distribuciones marginales se pueden obtener de la distribución conjunta.
Tenga en cuenta que
- \(\P(X \in A) = \P\left[(X, Y) \in A \times T\right]\)para\(A \subseteq S\)
- \(\P(Y \in B) = \P\left[(X, Y) \in S \times B\right]\)para\(B \subseteq T\)
Lo contrario no se sostiene en general. La distribución conjunta contiene mucha más información que las distribuciones marginales por separado. No obstante, lo contrario sí se sostiene si\(X\) y\(Y\) son independientes, como mostraremos a continuación.
Densidades articulares y marginales
Recordemos que las distribuciones de probabilidad a menudo se describen en términos de funciones de densidad de probabilidad. Nuestro objetivo es estudiar cómo las funciones de densidad de probabilidad de\( X \) e\( Y \) individualmente se relacionan con la función de densidad de probabilidad de\( (X, Y) \). Pero primero tenemos que asegurarnos de entender nuestro punto de partida.
Suponemos que\( (X, Y) \) tiene función de densidad\( f: S \times T \to (0, \infty) \) en el siguiente sentido:
- Si\( X \) y\( Y \) tienen distribuciones discretas en los conjuntos contables\( S \) y\( T \) respectivamente, entonces\( f \) se define por\[f(x, y) = \P(X = x, Y = y), \quad (x, y) \in S \times T\]
- Si\( X \) y\( Y \) tienen distribuciones continuas en\( S \subseteq \R^j \) y\( T \subseteq \R^k \) respectivamente, entonces\( f \) se define por la condición\[\P[(X, Y) \in C] = \int_C f(x, y) \, d(x, y), \quad C \subseteq S \times T\]
- En el caso mixto donde\( X \) tiene una distribución discreta en el conjunto contable\( S \) y\( Y \) tiene una distribución continua encendida\( T \subseteq R^k \), entonces\( f \) se define por la condición\[ \P(X = x, Y \in B) = \int_B f(x, y) \, dy, \quad x \in S, \; B \subseteq T \]
- En el caso mixto donde\( X \) tiene una distribución continua\( S \subseteq \R^j \) encendida y\( Y \) tiene una distribución discreta en el conjunto contable\( T \), entonces\( f \) se define por la condición\[ \P(X \in A, Y = y) = \int_A f(x, y), \, dx, \quad A \subseteq S, \; y \in T\]
Detalles
- En este caso,\( (X, Y) \) tiene una distribución discreta en el conjunto contable\( S \times T \) y\( f \) es la función de densidad con respecto a contar la medida\( \# \) en\( S \times T \).
- En este caso,\( (X, Y) \) tiene una distribución continua encendida\( S \times T \subseteq \R^{j+k} \) y\( f \) es la función de densidad con respecto a la medida de Lebesgue\( \lambda_{j+k} \) on\( S \times T \). La medida de Lebesgue, llamada así por Henri Lebesgue es la medida estándar en espacios euclidianos.
- En este caso, en\( (X, Y) \) realidad tiene una distribución continua:\[ \P[(X, Y) = (x, y) = \P(X = x, Y = y) \le \P(Y = y) = 0, \quad (x, y) \in S \times T \] La función\( f \) es la función de densidad con respecto a la medida del producto formada a partir de la medida de conteo\( \# \) en\( S \) y la medida de Lebesgue\( \lambda_k \) en\( T \).
- Este caso es igual que (c) pero con los roles de\( S \) y\( T \) revertidos. Una vez más,\( (X, Y) \) tiene una distribución continua y\( f \) es la función de densidad con respecto a la medida del producto en\( S \times T \) formado por Lebesgue medida\( \lambda_j \) en\( S \) y contando medida\( \# \) en\( T \).
En los casos (b), (c) y (d), no se garantiza la existencia de una función de densidad de probabilidad, sino que es una suposición que estamos haciendo. Los cuatro casos (y muchos otros) se pueden unificar bajo las teorías generales de medida e integración.
Primero veremos cómo obtener la función de densidad de probabilidad de una variable cuando la otra tiene una distribución discreta.
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) como se describió anteriormente.
- Si\( Y \) tiene una distribución discreta en el conjunto contable\( T \), entonces\( X \) tiene la función de densidad de probabilidad\( g \) dada por\(g(x) = \sum_{y \in T} f(x, y)\) for\(x \in S\)
- Si\( X \) tiene una distribución discreta en el conjunto contable\( S \), entonces\( Y \) tiene la función de densidad de probabilidad\( h \) dada por\(h(y) = \sum_{x \in S} f(x, y), \quad y \in T\)
Prueba
Los dos resultados son simétricos, por lo que probaremos (a). La herramienta principal es la propiedad de aditividad contable de probabilidad. Supongamos primero que\( X \) también tiene una distribución discreta en el conjunto contable\( S \). Entonces para\( x \in S \),\[ g(x) = \P(X = x) = \P(X = x, Y \in T) = \sum_{y \in T} \P(X = x, Y = y) = \sum_{y \in T} f(x, y) \] Supongamos siguiente que\( X \) tiene una distribución continua encendida\( S \subseteq \R^j \). Entonces para\( A \subseteq \R^j \),\[ \P(X \in A) = \P(X \in A, Y \in T) = \sum_{y \in T} \P(X \in A, Y = y) = \sum_{y \in T} \int_A f(x, y) \, dx = \int_A \sum_{y \in T} f(x, y), \, dx \] Se permite el intercambio de suma e integral ya que no\( f \) es negativo. Por el significado del término,\( X \) tiene función de densidad de probabilidad\( g \) dada por\( g(x) = \sum_{y \in T} f(x, y) \) for\( x \in S \)
A continuación veremos cómo obtener la función de densidad de probabilidad de una variable cuando la otra tiene una distribución continua.
Supongamos nuevamente que\((X, Y)\) tiene función de densidad de probabilidad\(f\) como se describió anteriormente.
- Si\( Y \) tiene una distribución continua en\( T \subseteq \R^k \) entonces\( X \) tiene la función de densidad de probabilidad\( g \) dada por\(g(x) = \int_T f(x, y) \, dy, \quad x \in S\)
- Si\( X \) tiene una distribución continua en\( S \subseteq \R^k \) entonces\( Y \) tiene la función de densidad de probabilidad\( h \) dada por\(h(y) = \int_S f(x, y) \, dx, \quad y \in T\)
Prueba
Nuevamente, los resultados son simétricos, por lo que mostramos (a). Supongamos primero que\( X \) tiene una distribución discreta en el conjunto contable\( S \). Entonces para\( x \in S \)\[ g(x) = \P(X = x) = \P(X = x, Y \in T) = \int_T f(x, y) \, dy \] Siguiente supongamos que\( X \) tiene una distribución continua encendida\( S \subseteq \R^j \). Entonces para\( A \subseteq S \),\[ \P(X \in A) = \P(X \in A, Y \in T) = \P\left[(X, Y) \in A \times T\right] = \int_{A \times T} f(x, y) \, d(x, y) = \int_A \int_T f(x, y) \, dy \] De ahí por el significado mismo del término,\( X \) tiene función de densidad de probabilidad\( g \) dada por\( g(x) = \int_T f(x, y) \, dy \) for\( x \in S \). Escribir la doble integral como una integral iterada es un caso especial del teorema de Fubini, llamado así por Guido Fubini.
En el contexto de los dos teoremas anteriores,\(f\) se llama la función conjunta de densidad de probabilidad de\((X, Y)\), mientras\(g\) y\(h\) se denominan las funciones de densidad marginal de\(X\) y de\(Y\), respectivamente. Algunos de los ejercicios computacionales a continuación dejarán claro el término marginal.
Independencia
Cuando las variables son independientes, las distribuciones marginales determinan la distribución conjunta.
Si\(X\) y\(Y\) son independientes, entonces la distribución\(X\) y la distribución de\(Y\) determinan la distribución de\((X, Y)\).
Prueba
Si\(X\) y\(Y\) son independientes entonces,\[\P\left[(X, Y) \in A \times B\right] = \P(X \in A, Y \in B) = \P(X \in A) \P(Y \in B) \quad A \in \mathscr S, \, B \in \mathscr T \] y como se señala en los detalles para (1), esto determina completamente la distribución\((X, Y)\) en\(S \times T\).
Cuando las variables son independientes, la densidad de juntas es el producto de las densidades marginales.
Supongamos que\(X\) y\(Y\) son independientes y tienen función de densidad de probabilidad\( g \) y\( h \) respectivamente. Entonces\((X, Y)\) tiene la función de densidad de probabilidad\(f\) dada por\[f(x, y) = g(x) h(y), \quad (x, y) \in S \times T\]
Prueba
La herramienta principal es el hecho de que un evento definido en términos de\( X \) es independiente de un evento definido en términos de\( Y \).
- Supongamos que\( X \) y\( Y \) tienen distribuciones discretas en los conjuntos contables\( S \) y\( T \) respectivamente. Entonces para\( (x, y) \in S \times T \),\[ \P\left[(X, Y) = (x, y)\right] = \P(X = x, Y = y) = \P(X = x) \P(Y = y) = g(x) h(y) \]
- Supongamos que a continuación eso\( X \) y\( Y \) tener distribuciones continuas sobre\( S \subseteq \R^j \) y\( T \subseteq \R^k \) respectivamente. Entonces para\( A \subseteq S \) y\( B \subseteq T \). \[ \P\left[(X, Y) \in A \times B\right] = \P(X \in A, Y \in B) = \P(X \in A) \P(Y \in B) = \int_A g(x) \, dx \, \int_B h(y) \, dy = \int_{A \times B} g(x) h(y) \, d(x, y) \]Como se señala en los detalles para (1), una medida de probabilidad on\( S \times T \) está completamente determinada por sus valores en conjuntos de productos, por lo que se deduce que\(\P\left[(X, Y) \in C\right] = \int_C f(x, y) \, d(x, y)\) para general\(C \subseteq S \times T\). De ahí\( (X, Y) \) que tenga PDF\( f \).
- Supongamos siguiente que\( X \) tiene una distribución discreta en el conjunto contable\( S \) y que\( Y \) tiene una distribución continua encendida\( T \subseteq \R^k \). Si\( x \in S \) y\( B \subseteq T \),\[ \P(X = x, Y \in B) = \P(X = x) \P(Y \in B) = g(x) \int_B h(y) \, dy = \int_B g(x) h(y) \, dy \] así de nuevo se deduce que\( (X, Y) \) tiene PDF\( f \). El caso en el\( X \) que tiene una distribución continua\( S \subseteq \R^j \)\( Y \) encendida y tiene una distribución discreta en el conjunto contable\( T \) es análogo.
El siguiente resultado da una conversa al último resultado. Si los factores de densidad de probabilidad conjunta en una función de\(x\) solo y una función de\(y\) solo, entonces\(X\) y\(Y\) son independientes, y casi podemos identificar las funciones de densidad de probabilidad individuales solo a partir del factoring.
Teorema de Factoring. Supongamos que\((X, Y)\) tiene función\(f\) de densidad de probabilidad de la forma\[f(x, y) = u(x) v(y), \quad (x, y) \in S \times T\] donde\(u: S \to [0, \infty)\) y\(v: T \to [0, \infty)\). Entonces\(X\) y\(Y\) son independientes, y existe una constante positiva\(c\) tal que\(X\) y\(Y\) tienen funciones de densidad de probabilidad\(g\) y\(h\), respectivamente, dadas por\ begin {align} g (x) = & c\, u (x),\ quad x\ in S\\ h (y) = &\ frac {1} {c} v (y),\ quad y\ en T\ final {align}
Prueba
Obsérvese que las pruebas en los diversos casos son esencialmente las mismas, salvo las sumas en el caso discreto y las integrales en el caso continuo.
- Supongamos que\( X \) y\( Y \) tienen distribuciones discretas en los conjuntos contables\( S \) y\( T \), respectivamente, para que\( (X, Y) \) tenga una distribución discreta encendida\( S \times T \). En este caso, la suposición es\[\P(X = x, Y = y) = u(x) v(y), \quad (x, y) \in S \times T\] Sumar\(y \in T\) en la ecuación mostrada da\(g(x) = \P(X = x) = c u(x)\) para\(x \in S\) dónde\(c = \sum_{y \in T} v(y)\). Del mismo modo, sumar\(x \in S\) en la ecuación mostrada da\(h(y) = \P(Y = y) = k v(y)\) para\(y \in T\) dónde\(k = \sum_{x \in S} u(y)\). Sumando\((x, y) \in S \times T\) en la ecuación mostrada da\(1 = c k\) así\(k = 1 / c\). Por último, sustituyendo da\(\P(X = x, Y = y) = \P(X = x) \P(Y = y)\) por\((x, y) \in S \times T\) así\(X\) y\(Y\) son independientes.
- Supongamos que a continuación eso\( X \) y\( Y \) tener distribuciones continuas sobre\( S \subseteq \R^j \) y\( T \subseteq \R^k \) respectivamente. Para\( A \subseteq S \) y\( B \subseteq T \),\[ \P(X \in A, Y \in B) = \P\left[(X, Y) \in A \times B\right] = \int_{A \times B} f(x, y) \, d(x, y) = \int_A u(x) \, dx \, \int_B v(y) dy \] Dejar\( B = T \) entrar la ecuación mostrada da\( \P(X \in A) = \int_A c \, u(x) \, dx \) para\( A \subseteq S \), donde\( c = \int_T v(y) \, dy \). Por definición,\( X \) tiene PDF\( g = c \, u \). A continuación, dejando\( A = S \) entrar la ecuación mostrada da\( \P(Y \in B) = \int_B k \, v(y) \, dy \) para\( B \subseteq T \), dónde\( k = \int_S u(x) \, dx \). Así,\( Y \) tiene PDF\( g = k \, v \). A continuación, dejar\( A = S \) y\( B = T \) en la ecuación mostrada da\( 1 = c \, k \), entonces\( k = 1 / c \). Ahora tenga en cuenta que la ecuación mostrada se mantiene con\( u \) reemplazada por\( g \) y\( v \) reemplazada por\( h \), y esto a su vez da\( \P(X \in A, Y \in B) = \P(X \in A) \P(Y \in B) \), así\( X \) y\( Y \) son independientes.
- Supongamos siguiente que\( X \) tiene una distribución discreta en el conjunto contable\( S \) y que\( Y \) tiene una distribución continua en\( T \subseteq \R^k \). Para\( x \in S \) y\( B \subseteq T \),\[ \P(X = x, Y \in B) = \int_B f(x, y) \, dy = u(x) \int_B v(y) \, dy \] Dejar\( B = T \) entrar la ecuación mostrada da\( \P(X \in x) = c \, u(x) \) para\( x \in S \), donde\( c = \int_T v(y) \, dy \). Así lo\( X \) ha hecho PDF\( g = c \, u \). A continuación, sumar\( x \in S \) en la ecuación mostrada da\( \P(Y \in B) = k \int_B \, v(y) \, dy \) para\( B \subseteq T \), dónde\( k = \sum_{x \in S} u(x) \). Así,\( Y \) tiene PDF\( g = k \, v \). A continuación, sumar\( x \in S \) y dejar\( B = T \) entrar la ecuación mostrada da\( 1 = c \, k \), entonces\( k = 1 / c \). Ahora tenga en cuenta que la ecuación mostrada se mantiene con\( u \) reemplazada por\( g \) y\( v \) reemplazada por\( h \), y esto a su vez da\( \P(X = x, Y \in B) = \P(X = x) \P(Y \in B) \), así\( X \) y\( Y \) son independientes. El caso donde donde\( X \) tiene una distribución continua\( S \subseteq \R^j \) encendida y\( Y \) tiene una distribución discreta en el conjunto contable\( T \) es análogo.
Los dos últimos resultados se extienden a más de dos variables aleatorias, porque\(X\) y\(Y\) ellos mismos pueden ser vectores aleatorios. Aquí está la declaración explícita:
Supongamos que\(X_i\) es una variable aleatoria tomando valores en un conjunto\(R_i\) con función de densidad de probabilidad\(g_i\) para\(i \in \{1, 2, \ldots, n\}\), y que las variables aleatorias son independientes. Entonces el vector aleatorio\(\bs X = (X_1, X_2, \ldots, X_n)\) que toma valores\(S = R_1 \times R_2 \times \cdots \times R_n\) tiene la función de densidad de probabilidad\(f\) dada por\[f(x_1, x_2, \ldots, x_n) = g_1(x_1) g_2(x_2) \cdots g_n(x_n), \quad (x_1, x_2, \ldots, x_n) \in S\]
El caso especial donde las distribuciones son todas iguales es particularmente importante.
Supongamos que\(\bs X = (X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias independientes, cada una tomando valores en un conjunto\(R\) y con función de densidad de probabilidad común\(g\). Entonces la función\(f\) de densidad de probabilidad de\(\bs X\) on\(S = R^n\) viene dada por\[f(x_1, x_2, \ldots, x_n) = g(x_1) g(x_2) \cdots g(x_n), \quad (x_1, x_2, \ldots, x_n) \in S\]
En jerga de probabilidad,\(\bs X\) es una secuencia de variables independientes, distribuidas idénticamente, una frase que aparece tan a menudo que a menudo se abrevia como IID. En la jerga estadística,\(\bs X\) es una muestra aleatoria de tamaño\(n\) de la distribución común. Como se desprende de la terminología especial, esta situación es muy impotante en ambas ramas de la matemática. En estadística, la función conjunta de densidad de probabilidad\(f\) juega un papel importante en procedimientos como la máxima verosimilitud y la identificación de mejores estimadores uniformemente.
Recordemos que la independencia (mutua) de las variables aleatorias es una propiedad muy fuerte. Si una colección de variables aleatorias es independiente, entonces cualquier subcolección también es independiente. Las nuevas variables aleatorias formadas a partir de subcolecciones disjuntas son independientes. Para un ejemplo sencillo, supongamos que\(X\),\(Y\), y\(Z\) son variables aleatorias independientes de valor real. Entonces
- \(\sin(X)\),\(\cos(Y)\), y\(e^Z\) son independientes.
- \((X, Y)\)y\(Z\) son independientes.
- \(X^2 + Y^2\)y\(\arctan(Z)\) son independientes.
- \(X\)y\(Z\) son independientes.
- \(Y\)y\(Z\) son independientes.
En particular, señalar que el enunciado 2 de la lista anterior es mucho más fuerte que la conjunción de los enunciados 4 y 5. Reexpresado, si\(X\) y\(Z\) son dependientes, entonces\((X, Y)\) y también\(Z\) son dependientes.
Ejemplos y Aplicaciones
Dados
Recordemos que una matriz estándar es una matriz ordinaria de seis caras, con caras numeradas del 1 al 6. Las respuestas en el siguiente par de ejercicios dan la distribución conjunta en el cuerpo de una tabla, con las distribuciones marginales literalmente en los magines. Tales tablas son la razón del término distribución marginal.
Supongamos que se lanzan dos dados estándar y justos y se\((X_1, X_2)\) registra la secuencia de puntuaciones. Nuestra suposición ususal es que las variables\(X_1\) y\(X_2\) son independientes. Dejar\(Y = X_1 + X_2\) y\(Z = X_1 - X_2\) denotar la suma y diferencia de los puntajes, respectivamente.
- Encuentra la función de densidad de probabilidad de\((Y, Z)\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- Encuentra la función de densidad de probabilidad de\(Z\).
- ¿Son\(Y\) e\(Z\) independientes?
Contestar
Dejar\(f\) denotar el PDF de\((Y, Z)\),\(g\) el PDF de\(Y\) y\(h\) el PDF de\(Z\). Los PDF se dan en la siguiente tabla. Variables aleatorias\(Y\) y\(Z\) son dependientes
| \(f(y, z)\) | \(y = 2\) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 11 | 12 | \(h(z)\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(z = -5\) | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) |
| \(-4\) | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | \(\frac{2}{36}\) |
| \(-3\) | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | \(\frac{3}{36}\) |
| \(-2\) | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | \(\frac{4}{36}\) |
| \(-1\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{5}{36}\) |
| 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | \(\frac{6}{36}\) |
| 1 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{5}{36}\) |
| 2 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | \(\frac{4}{36}\) |
| 3 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | \(\frac{3}{36}\) |
| 4 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | \(\frac{2}{36}\) |
| 5 | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) |
| \(g(y)\) | \(\frac{1}{36}\) | \(\frac{2}{36}\) | \(\frac{3}{36}\) | \(\frac{4}{36}\) | \(\frac{5}{36}\) | \(\frac{6}{36}\) | \(\frac{5}{36}\) | \(\frac{4}{36}\) | \(\frac{3}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 1 |
Supongamos que se lanzan dos dados estándar y justos y se\((X_1, X_2)\) registra la secuencia de puntuaciones. Dejar\(U = \min\{X_1, X_2\}\) y\(V = \max\{X_1, X_2\}\) denotar las puntuaciones mínimas y máximas, respectivamente.
- Encuentra la función de densidad de probabilidad de\((U, V)\).
- Encuentra la función de densidad de probabilidad de\(U\).
- Encuentra la función de densidad de probabilidad de\(V\).
- ¿Son\(U\) e\(V\) independientes?
Contestar
Dejar\(f\) denotar el PDF de\((U, V)\),\(g\) el PDF de\(U\), y\(h\) el PDF de\(V\). Los PDF se dan en la siguiente tabla. Variables aleatorias\(U\) y\(V\) son dependientes.
| \(f(u, v)\) | \(u = 1\) | 2 | 3 | 4 | 5 | 6 | \(h(v)\) |
|---|---|---|---|---|---|---|---|
| \(v = 1\) | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | 0 | \(\frac{1}{36}\) |
| 2 | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 0 | 0 | 0 | 0 | \(\frac{3}{36}\) |
| 3 | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 0 | 0 | 0 | \(\frac{5}{36}\) |
| 4 | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 0 | 0 | \(\frac{7}{36}\) |
| 5 | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | 0 | \(\frac{9}{36}\) |
| 6 | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) | \(\frac{11}{36}\) |
| \(g(u)\) | \(\frac{11}{36}\) | \(\frac{9}{36}\) | \(\frac{7}{36}\) | \(\frac{5}{36}\) | \(\frac{3}{36}\) | \(\frac{1}{36}\) | 1 |
Los dos ejercicios anteriores muestran claramente cuán poca información se da con las distribuciones marginales en comparación con la distribución conjunta. Solo con los PDF marginales, ni siquiera se pudo determinar el conjunto de soporte de la distribución conjunta, y mucho menos los valores del PDF conjunto.
Distribuciones Continuas Simples
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = x + y\) for\(0 \le x \le 1\),\(0 \le y \le 1\).
- Encuentra la función de densidad de probabilidad de\(X\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(X\)tiene PDF\(g\) dado por\(g(x) = x + \frac{1}{2}\) para\(0 \le x \le 1\)
- \(Y\)tiene PDF\(h\) dado por\(h(y) = y + \frac{1}{2}\) para\(0 \le y \le 1\)
- \(X\)y\(Y\) son dependientes.
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = 2 ( x + y)\) for\(0 \le x \le y \le 1\).
- Encuentra la función de densidad de probabilidad de\(X\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(X\)tiene PDF\(g\) dado por\(g(x) = (1 + 3 x)(1 - x)\) for\(0 \le x \le 1\).
- \(Y\)tiene PDF\(h\) dado por\(h(h) = 3 y^2\) for\(0 \le y \le 1\).
- \(X\)y\(Y\) son dependientes.
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = 6 x^2 y\) for\(0 \le x \le 1\),\(0 \le y \le 1\).
- Encuentra la función de densidad de probabilidad de\(X\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(X\)tiene PDF\(g\) dado por\(g(x) = 3 x^2\) for\(0 \le x \le 1\).
- \(Y\)tiene PDF\(h\) dado por\(h(y) = 2 y\) for\(0 \le y \le 1\).
- \(X\)y\(Y\) son independientes.
El último ejercicio es una buena ilustración del teorema de factorización. Sin ningún trabajo en absoluto, podemos decir que el PDF de\(X\) es proporcional a\(x \mapsto x^2\) sobre el intervalo\([0, 1]\), el PDF de\(Y\) es proporcional a\(y \mapsto y\) en el intervalo\([0, 1]\), y eso\(X\) y\(Y\) son independientes. Lo único poco claro es cómo los constantes 6 factores.
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = 15 x^2 y\) for\(0 \le x \le y \le 1\).
- Encuentra la función de densidad de probabilidad de\(X\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(X\)tiene PDF\(g\) dado por\(g(x) = \frac{15}{2} x^2 \left(1 - x^2\right)\) for\(0 \le x \le 1\).
- \(Y\)tiene PDF\(h\) dado por\(h(y) = 5 y^4\) for\(0 \le y \le 1\).
- \(X\)y\(Y\) son dependientes.
Obsérvese que en el último ejercicio, no se aplica el teorema de factorización. Las variables aleatorias\(X\) y\(Y\) cada una toman valores en\([0, 1]\), pero los factores PDF conjuntos solo en parte de\([0, 1]^2\).
Supongamos que\((X, Y, Z)\) tiene función de densidad de probabilidad\(f\) dada\(f(x, y, x) = 2 (x + y) z\) para\(0 \le x \le 1\),\(0 \le y \le 1\),\(0 \le z \le 1\).
- Encuentra la función de densidad de probabilidad de cada par de variables.
- Encuentra la función de densidad de probabilidad de cada variable.
- Determinar las relaciones de dependencia entre las variables.
Prueba
- \((X, Y)\)tiene PDF\(f_{1,2}\) dado por\(f_{1,2}(x,y) = x + y\) for\(0 \le x \le 1\),\(0 \le y \le 1\).
- \((X, Z)\)tiene PDF\(f_{1,3}\) dado por\(f_{1,3}(x,z) = 2 z \left(x + \frac{1}{2}\right)\) for\(0 \le x \le 1\),\(0 \le z \le 1\).
- \((Y, Z)\)tenía PDF\(f_{2,3}\) dado por\(f_{2,3}(y,z) = 2 z \left(y + \frac{1}{2}\right)\) para\(0 \le y \le 1\),\(0 \le z \le 1\).
- \(X\)tiene PDF\(f_1\) dado por\(f_1(x) = x + \frac{1}{2}\) for\(0 \le x \le 1\).
- \(Y\)tiene PDF\(f_2\) dado por\(f_2(y) = y + \frac{1}{2}\) for\(0 \le y \le 1\).
- \(Z\)tiene PDF\(f_3\) dado por\(f_3(z) = 2 z\) for\(0 \le z \le 1\).
- \(Z\)y\((X, Y)\) son independientes;\(X\) y\(Y\) son dependientes.
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada por\(f(x, y) = 2 e^{-x} e^{-y}\) for\(0 \le x \le y \lt \infty\).
- Encuentra la función de densidad de probabilidad de\(X\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(X\)tiene PDF\(g\) dado por\(g(x) = 2 e^{-2 x}\) for\(0 \le x \lt \infty\).
- \(Y\)tiene PDF\(h\) dado por\(h(y) = 2 \left(e^{-y} - e^{-2y}\right)\) for\(0 \le y \lt \infty\).
- \(X\)y\(Y\) son dependientes.
En el ejercicio anterior,\( X \) tiene una distribución exponencial con el parámetro de tasa 2. Recordemos que las distribuciones exponenciales son ampliamente utilizadas para modelar tiempos aleatorios, particularmente en el contexto del modelo de Poisson.
Supongamos que\(X\) y\(Y\) son independientes, y que\(X\) tiene función de densidad de probabilidad\(g\) dada por\(g(x) = 6 x (1 - x)\) for\(0 \le x \le 1\), y que\(Y\) tiene función de densidad de probabilidad\(h\) dada por\(h(y) = 12 y^2 (1 - y)\) for\(0 \le y \le 1\).
- Encuentra la función de densidad de probabilidad de\((X, Y)\).
- Encuentra\(\P(X + Y \le 1)\).
Contestar
- \((X, Y)\)tiene PDF\(f\) dado por\(f(x, y) = 72 x (1 - x) y^2 (1 - y)\) for\(0 \le x \le 1\),\(0 \le y \le 1\).
- \(\P(X + Y \le 1) = \frac{13}{35}\)
En el ejercicio anterior,\( X \) y\( Y \) cuentan con distribuciones beta, las cuales son ampliamente utilizadas para modelar probabilidades y proporciones aleatorias. Las distribuciones beta se estudian con más detalle en el capítulo sobre Distribuciones especiales.
Supongamos que\(\Theta\) y\(\Phi\) son ángulos aleatorios independientes, con función de densidad de probabilidad común\(g\) dada por\(g(t) = \sin(t)\) for\(0 \le t \le \frac{\pi}{2}\).
- Encuentra la función de densidad de probabilidad de\((\Theta, \Phi)\).
- Encuentra\(\P(\Theta \le \Phi)\).
Contestar
- \((\Theta, \Phi)\)tiene PDF\(f\) dado por\(f(\theta, \phi) = \sin(\theta) \sin(\phi)\) for\(0 \le \theta \le \frac{\pi}{2}\),\(0 \le \phi \le \frac{\pi}{2}\).
- \(\P(\Theta \le \Phi) = \frac{1}{2}\)
La distribución común\( X \) y\( Y \) en el ejercicio anterior gobierna un ángulo aleatorio en el problema de Bertrand.
Supongamos que\(X\) y\(Y\) son independientes, y que\(X\) tiene función de densidad de probabilidad\(g\) dada por\(g(x) = \frac{2}{x^3}\) for\(1 \le x \lt \infty\), y que\(Y\) tiene función de densidad de probabilidad\(h\) dada por\(h(y) = \frac{3}{y^4}\) for\(1 \le y \lt\infty\).
- Encuentra la función de densidad de probabilidad de\((X, Y)\).
- Encuentra\(\P(X \le Y)\).
Contestar
- \((X, Y)\)tiene PDF\(f\) dado por\(f(x, y) = \frac{6}{x^3 y^4}\) for\(1 \le x \lt \infty\),\(1 \le y \lt \infty\).
- \(\P(X \le Y) = \frac{2}{5}\)
Ambos\(X\) y\(Y\) en el ejercicio anterior tienen distribuciones de Pareto, llamadas así por Vilfredo Pareto. Recordemos que las distribuciones de Pareto se utilizan para modelar ciertas variables económicas y se estudian con más detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(g\) dada por\(g(x, y) = 15 x^2 y\) for\(0 \le x \le y \le 1\), y que\(Z\) tiene función de densidad de probabilidad\(h\) dada por\(h(z) = 4 z^3\) for\(0 \le z \le 1\), y que\((X, Y)\) y\(Z\) son independientes.
- Encuentra la función de densidad de probabilidad de\((X, Y, Z)\).
- Encuentra la función de densidad de probabilidad de\((X, Z)\).
- Encuentra la función de densidad de probabilidad de\((Y, Z)\).
- Encuentra\(\P(Z \le X Y)\).
Contestar
- \((X, Y, Z)\)tiene PDF\(f\) dado por\(f(x, y, z) = 60 x^2 y z^3\) for\(0 \le x \le y \le 1\),\(0 \le z \le 1\).
- \((X, Z)\)tiene PDF\(f_{1,3}\) dado por\(f_{1,3}(x, z) = 30 x^2 \left(1 - x^2\right) z^3\) for\(0 \le x \le 1\),\(0 \le z \le 1\).
- \((Y, Z)\)tiene PDF\(f_{2,3}\) dado por\(f_{2,3}(y, z) = 20 y^4 z^3\) for\(0 \le y \le 1\),\(0 \le z \le 1\).
- \(\P(Z \le X Y) = \frac{15}{92}\)
Distribuciones Uniformes Multivariadas
Las distribuciones uniformes multivariadas dan una interpretación geométrica de algunos de los conceptos de esta sección.
Recordemos primero que para\( n \in \N_+ \), la medida estándar en\(\R^n\) es\[\lambda_n(A) = \int_A 1 dx, \quad A \subseteq \R^n\] En particular,\(\lambda_1(A)\) es la longitud de\(A \subseteq \R\),\(\lambda_2(A)\) es el área de\(A \subseteq \R^2\), y\(\lambda_3(A)\) es el volumen de\(A \subseteq \R^3\).
Detalles
Técnicamente\(\lambda_n\) es Lebesgue medida en los subconjuntos medibles de\(\R^n\). La representación integral es válida para los tipos de conjuntos que ocurren en las aplicaciones. En la discusión a continuación, se supone que todos los subconjuntos son medibles.
Supongamos ahora que\(X\) toma valores\(\R^j\),\(Y\) toma valores en\(\R^k\), y que\((X, Y)\) se distribuye uniformemente en un conjunto\(R \subseteq \R^{j+k}\). Entonces\(0 \lt \lambda_{j+k}(R) \lt \infty \) y la función conjunta de densidad de probabilidad\( f \) de\((X, Y)\) está dada por\( f(x, y) = 1 \big/ \lambda_{j+k}(R) \) for\( (x, y) \in R \). Recordemos que las distribuciones uniformes siempre tienen funciones de densidad constante. Ahora dejemos\(S\) y\(T\) sean las proyecciones de\(R\) onto\(\R^j\) y\(\R^k\) respectivamente, definidas de la siguiente manera:\[ S = \left\{x \in \R^j: (x, y) \in R \text{ for some } y \in \R^k\right\}, \; T = \left\{y \in \R^k: (x, y) \in R \text{ for some } x \in \R^j\right\}\] Obsérvese eso\(R \subseteq S \times T\). A continuación denotamos las secciones transversales en\(x \in S\) y en\(y \in T\), respectivamente, por\[T_x = \{t \in T: (x, t) \in R\}, \; S_y = \{s \in S: (s, y) \in R\}\]
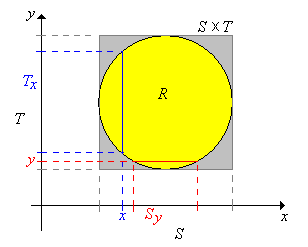
\(X\)toma valores\(S\) y\( Y \) toma valores en\( T \). Las funciones de densidad de probabilidad\(g\) y\( h \) de\(X\) y\( Y \) son proporcionales a las medidas transversales:
- \( g(x) = \lambda_k\left(T_x\right) \big/ \lambda_{j+k}(R) \)para\( x \in S \)
- \( h(y) = \lambda_j\left(S_y\right) \big/ \lambda_{j+k}(R) \)para\( y \in T \)
Prueba
De nuestra teoría general,\( X \) tiene PDF\( g \) dado por\[ g(x) = \int_{T_x} f(x, y) \, dy = \int_{T_x} \frac{1}{\lambda_{j+k}(R)} \, dy = \frac{\lambda_k\left(T_x\right)}{\lambda_{j+k}(R)}, \quad x \in S \] Técnicamente, es posible que\(\lambda_k(T_x) = \infty\) para algunos\(x \in S\), pero el conjunto de tales\(x\) tenga medida 0. Es decir,\(\lambda_j\{x \in S: \lambda_k(T_x) = \infty\} = 0\). El resultado para\( Y \) es análogo.
En particular, señalar del teorema anterior que\(X\) y no\(Y\) son independientes ni uniformemente distribuidos en general. Sin embargo, estas propiedades se mantienen si\(R\) es un conjunto de productos cartesianos.
Supongamos que\(R = S \times T\).
- \(X\)se distribuye uniformemente en\(S\).
- \(Y\)se distribuye uniformemente en\(T\).
- \(X\)y\(Y\) son independientes.
Prueba
En este caso,\( T_x = T \) y\( S_y = S \) para cada\( x \in S \) y\( y \in T \). También,\( \lambda_{j+k}(R) = \lambda_j(S) \lambda_k(T) \), así para\( x \in S \) y\( y \in T \),\( f(x, y) = 1 \big/ [\lambda_j(S) \lambda_k(T)] \),\( g(x) = 1 \big/ \lambda_j(S) \),\( h(y) = 1 \big/ \lambda_k(T) \).
En cada uno de los siguientes casos, encontrar las funciones de densidad probabilit conjunta y marginal, y determinar si\(X\) y\(Y\) son independientes.
- \((X, Y)\)se distribuye uniformemente en el cuadrado\(R = [-6, 6]^2\).
- \((X, Y)\)se distribuye uniformemente en el triángulo\(R = \{(x, y): -6 \le y \le x \le 6\}\).
- \((X, Y)\)se distribuye uniformemente en el círculo\(R = \left\{(x, y): x^2 + y^2 \le 36\right\}\).
Contestar
A continuación,\(f\) se encuentra el PDF de\((X, Y)\),\(g\) el PDF de\(X\), y\(h\) el PDF de\(Y\).
-
- \(f(x, y) = \frac{1}{144}\)para\(-6 \le x \le 6\),\(-6 \le y \le 6\)
- \(g(x) = \frac{1}{12}\)para\(-6 \le x \le 6\)
- \(h(y) = \frac{1}{12}\)para\(-6 \le y \le 6\)
- \(X\)y\(Y\) son independientes.
-
- \(f(x, y) = \frac{1}{72}\)para\(-6 \le y \le x \le 6\)
- \(g(x) = \frac{1}{72}(x + 6)\)para\(-6 \le x \le 6\)
- \(h(y) = \frac{1}{72}(y + 6)\)para\(-6 \le y \le 6\)
- \(X\)y\(Y\) son dependientes.
-
- \(f(x, y) = \frac{1}{36 \pi}\)para\(x^2 + y^2 \le 36\)
- \(g(x) = \frac{1}{18 \pi} \sqrt{36 - x^2}\)para\(-6 \le x \le 6\)
- \(h(y) = \frac{1}{18 \pi} \sqrt{36 - y^2}\)para\(-6 \le y \le 6\)
- \(X\)y\(Y\) son dependientes.
En el experimento uniforme bivariado, ejecute la simulación 1000 veces para cada uno de los siguientes casos. Observe los puntos en la gráfica de dispersión y las gráficas de las distribuciones marginales. Interpreta lo que ves en el contexto de la discusión anterior.
- cuadrado
- triángulo
- círculo
Supongamos que\((X, Y, Z)\) se distribuye uniformemente sobre el cubo\([0, 1]^3\).
- Dar la función de densidad de probabilidad conjunta de\((X, Y, Z)\).
- Encuentra la función de densidad de probabilidad de cada par de variables.
- Encuentra la función de densidad de probabilidad de cada variable
- Determinar las relaciones de dependencia entre las variables.
Contestar
- \((X, Y, Z)\)tiene PDF\(f\) dado por\(f(x, y, z) = 1\) for\(0 \le x \le 1\),\(0 \le y \le 1\),\(0 \le z \le 1\) (la distribución uniforme en\([0, 1]^3\))
- \((X, Y)\),\((X, Z)\), y\((Y, Z)\) tener PDF común\(g\) dado por\(g(u, v) = 1\) for\(0 \le u \le 1\),\(0 \le v \le 1\) (la distribución uniforme en\([0, 1]^2\))
- \(X\),\(Y\), y\(Z\) tener PDF común\(h\) dado por\(h(u) = 1\) for\(0 \le u \le 1\) (la distribución uniforme en\([0, 1]\))
- \(X\),\(Y\),\(Z\) son independientes.
Supongamos que\((X, Y, Z)\) se distribuye uniformemente en\(\{(x, y, z): 0 \le x \le y \le z \le 1\}\).
- Dar la función de densidad articular de\((X, Y, Z)\).
- Encuentra la función de densidad de probabilidad de cada par de variables.
- Encuentra la función de densidad de probabilidad de cada variable
- Determinar las relaciones de dependencia entre las variables.
Contestar
- \((X, Y, Z)\)tiene PDF\(f\) dado por\(f(x, y, z) = 6\) para\(0 \le x \le y \le z \le 1\)
-
- \((X, Y)\)tiene PDF\(f_{1,2}\) dado por\(f_{1,2}(x, y) = 6 (1 - y)\) para\(0 \le x \le y \le 1\)
- \((X, Z)\)tiene PDF\(f_{1,3}\) dado por\(f_{1,3}(x, z) = 6 (z - x)\) para\(0 \le x \le z \le 1\)
- \((Y, Z)\)tiene PDF\(f_{2,3}\) dado por\(f_{2,3}(y, z) = 6 y\) para\(0 \le y \le z \le 1\)
-
- \(X\)tiene PDF\(f_1\) dado por\(f_1(x) = 3 (1 - x)^2\) para\(0 \le x \le 1\)
- \(Y\)tiene PDF\(f_2\) dado por\(f_2(y) = 6 y (1 - y)\) para\(0 \le y \le 1\)
- \(Z\)tiene PDF\(f_3\) dado por\(f_3(z) = 3 z^2\) para\(0 \le z \le 1\)
- Cada par de variables es dependiente.
El Método de Rechazo
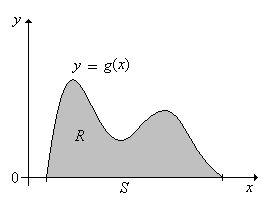
El siguiente resultado muestra cómo se puede obtener una distribución continua arbitraria a partir de una distribución uniforme. Este resultado es útil para simular ciertas distribuciones continuas, como veremos. Para configurar la notación básica, supongamos que\(g\) es una función de densidad de probabilidad para una distribución continua en\(S \subseteq \R^n\). Let\[R = \{(x, y): x \in S \text{ and } 0 \le y \le g(x)\} \subseteq \R^{n+1} \]
Si\((X, Y)\) se distribuye uniformemente en\(R\), entonces\(X\) tiene la función de densidad de probabilidad\(g\).
Prueba
Tenga en cuenta que ya\(g\) es una función de densidad de probabilidad en\(S\). \[ \lambda_{n+1}(R) = \int_R 1 \, d(x, y) = \int_S \int_0^{g(x)} 1 \, dy \, dx = \int_S g(x) \, dx = 1 \]De ahí que la función\( f \) de densidad de probabilidad de\((X, Y)\) viene dada por\(f(x, y) = 1\) for\((x, y) \in R\). Así, la función de densidad de probabilidad de\(X\) es\(x \mapsto \int_0^{g(x)} 1 \, dy = g(x)\) para\( x \in S \).
Una imagen en el caso\(n = 1\) se da a continuación:
El siguiente resultado da el método de rechazo para simular una variable aleatoria con la función de densidad de probabilidad\(g\).
Supongamos ahora que\( R \subseteq T \) donde\( T \subseteq \R_{n+1} \) con\( \lambda_{n+1}(T) \lt \infty \) y que\(\left((X_1, Y_1), (X_2, Y_2), \ldots\right)\) es una secuencia de variables aleatorias independientes con\( X_k \in \R^n \),\( Y_k \in \R \), y\( \left(X_k, Y_k\right) \) uniformemente distribuidas en\( T \) para cada una\( k \in \N_+ \). Let\[N = \min\left\{k \in \N_+: \left(X_k, Y_k\right) \in R\right\} = \min\left\{k \in \N_+: X_k \in S, \; 0 \le Y_k \le g\left(X_k\right)\right\}\]
- \( N \)tiene la distribución geométrica en el parámetro\(\N_+\) con éxito\( p = 1 / \lambda_{n+1}(T) \).
- \(\left(X_N, Y_N\right)\)se distribuye uniformemente en\(R\).
- \(X_N\)tiene función de densidad de probabilidad\(g\).
Prueba
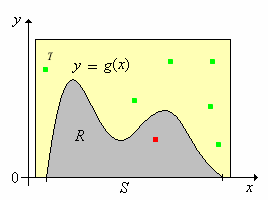
El punto del teorema es que si podemos simular una secuencia de variables independientes que se distribuyen uniformemente en\( T \), entonces podemos simular una variable aleatoria con la función de densidad de probabilidad dada\( g \). Supongamos en particular que\( R \) está delimitado como un subconjunto de\( \R^{n+1} \), lo que significaría que el dominio\( S \) está limitado como un subconjunto de\( \R^n \) y que la función de densidad de probabilidad\( g \) está limitada en\( S \). En este caso, podemos encontrar\( T \) que es el producto cartesiano de intervalos\( n + 1 \) acotados con\( R \subseteq T \). Resulta muy fácil simular una secuencia de variables independientes, cada una distribuida uniformemente en dicho conjunto de productos, por lo que el método de rechazo siempre funciona en este caso. Como puedes adivinar, el método de rechazo funciona mejor si el tamaño de\( T \), es decir\( \lambda_{n+1}(T) \), es pequeño, de modo que el parámetro de éxito\( p \) es grande.
La app método de rechazo simula una serie de distribuciones continuas a través del método de rechazo. Para cada una de las siguientes distribuciones, varíe los parámetros y anote la forma y ubicación de la función de densidad de probabilidad. Después, ejecute el experimento 1000 veces y observe los resultados.
- La distribución beta
- La distribución del semicírculo
- La distribución del triángulo
- La distribución de energía U
La distribución hipergeométrica multivariada
Supongamos que una población consiste en\(m\) objetos, y que cada objeto es uno de cuatro tipos. Hay objetos\(a\) tipo 1,\(b\) tipo 2 objetos,\(c\) tipo 3 objetos y\(m - a - b - c\) tipo 0 objetos. Muestreamos\(n\) objetos de la población al azar, y sin reemplazo. Los parámetros\(m\)\(a\),\(b\),\(c\), y\(n\) son enteros no negativos con\(a + b + c \le m\) y\(n \le m\). Denote el número de objetos tipo 1, 2 y 3 en la muestra por\(X\)\(Y\), y\(Z\), respectivamente. De ahí que el número de objetos tipo 0 en la muestra sea\(n - X - Y - Z\). En los problemas a continuación, las variables\(x\)\(y\),, y\(z\) toman valores\(\N\).
\((X, Y, Z)\)tiene una distribución hipergeométrica (multivariada) con función de densidad de probabilidad\(f\) dada por\[f(x, y, z) = \frac{\binom{a}{x} \binom{b}{y} \binom{c}{z} \binom{m - a - b - c}{n - x - y - z}}{\binom{m}{n}}, \quad x + y + z \le n\]
Prueba
A partir de la teoría básica de la combinatoria, el numerador es el número de formas de seleccionar una muestra desordenada\( n \) de tamaño de la población con\( x \) objetos de tipo 1,\( y \) objetos de tipo 2,\( z \) objetos de tipo 3 y\( n - x - y - z \) objetos de tipo 0. El denominador es el número total de formas de seleccionar la muestra desordenada.
\((X, Y)\)también tiene una distribución hipergeométrica (multivariada), con la función de densidad de probabilidad\(g\) dada por\[g(x, y) = \frac{\binom{a}{x} \binom{b}{y} \binom{m - a - b}{n - x - y}}{\binom{m}{n}}, \quad x + y \le n\]
Prueba
Este resultado podría obtenerse sumando el PDF conjunto\( z \) para fijo\( (x, y) \). Sin embargo, hay un argumento combinatorio mucho más agradable. Tenga en cuenta que estamos seleccionando una muestra aleatoria\(n\) de tamaño de una población de\(m\) objetos, con\(a\) objetos de tipo 1,\(b\) objetos de tipo 2 y\(m - a - b\) objetos de otro tipo.
\(X\)tiene una distribución hipergeométrica ordinaria, con la función de densidad de probabilidad\(h\) dada por\[h(x) = \frac{\binom{a}{x} \binom{m - a}{n - x}}{\binom{m}{n}}, \quad x \le n\]
Prueba
Nuevamente, el resultado podría obtenerse sumando el PDF conjunto para\( (X, Y, Z) \) más\( (y, z) \) para fijo\( x \), o sumando el PDF conjunto para\( (X, Y) \) más\( y \) para fijo\( x \). Pero como antes, hay un argumento combinatorio mucho más elegante. Tenga en cuenta que estamos seleccionando una muestra aleatoria de tamaño\(n\) de una población de\(m\) objetos de tamaño, con\(a\) objetos de tipo 1 y\(m - a\) objetos de otro tipo.
Estos resultados generalizan de manera directa a una población con cualquier número de tipos. En resumen, si un vector aleatorio tiene una distribución hipergeométrica, entonces cualquier subvector también tiene una distribución hipergeométrica. En otras palabras, todas las distribuciones marginales de una distribución hipergeométrica son en sí mismas hipergeométricas. Tenga en cuenta sin embargo, que no es buena idea memorizar explícitamente las fórmulas anteriores. Es mejor solo anotar los patrones y recordar el significado combinatorio del coeficiente binomial. La distribución hipergeométrica y la distribución hipergeométrica multivariada se estudian con más detalle en el capítulo Modelos de Muestreo Finito.
Supongamos que una población de votantes está formada por 50 demócratas, 40 republicanos y 30 independientes. Se elige al azar una muestra de 10 electores de la población (sin reemplazo, por supuesto). Vamos a\(X\) denotar el número de demócratas en la muestra y\(Y\) el número de republicanos en la muestra. Encuentre la función de densidad de probabilidad de cada uno de los siguientes:
- \((X, Y)\)
- \(X\)
- \(Y\)
Contestar
En las fórmulas para los PDF a continuación, las variables\(x\) y\(y\) son enteros no negativos.
- \((X, Y)\)tiene PDF\(f\) dado por\(f(x, y) = \frac{1}{\binom{120}{10}} \binom{50}{x} \binom{40}{y} \binom{30}{10 - x - y}\) para\(x + y \le 10\)
- \(X\)tiene PDF\(g\) dado por\(g(x) = \frac{1}{\binom{120}{10}} \binom{50}{x} \binom{70}{10 - x}\) para\(x \le 10\)
- \(Y\)tiene PDF\(h\) dado por\(h(y) = \frac{1}{\binom{120}{10}} \binom{40}{y} \binom{80}{10 - y}\) para\(y \le 10\)
Supongamos que el Club de Matemáticas de Enormous State University (ESU) cuenta con 50 estudiantes de primer año, 40 estudiantes de segundo año, 30 juniors y 20 seniors. Una muestra de 10 miembros del club se elige al azar para servir en el comité\(\pi\) del día. Que\(X\) denote el número de estudiantes de primer año en\(Y\) el comité, el número de estudiantes de segundo año, y\(Z\) el número de juniors.
- Encuentra la función de densidad de probabilidad de\((X, Y, Z)\)
- Encuentra la función de densidad de probabilidad de cada par de variables.
- Encuentra la función de densidad de probabilidad de cada variable individual.
Contestar
En las fórmulas para los PDF a continuación, las variables\(x\),\(y\), y\(z\) son números enteros no negativos.
- \((X, Y, Z)\)tiene PDF\(f\) dado por\(f(x, y, z) = \frac{1}{\binom{140}{10}} \binom{50}{x} \binom{40}{y} \binom{30}{z} \binom{20}{10 - x - y - z}\) for\(x + y + z \le 10\).
-
- \((X, Y)\)tiene PDF\(f_{1,2}\) dado por\(f_{1,2}(x, y) = \frac{1}{\binom{140}{10}} \binom{50}{x} \binom{40}{y} \binom{50}{10 - x - y}\) for\(x + y \le 10\).
- \((X, Z)\)tiene PDF\(f_{1,3}\) dado por\(f_{1,3}(y, z) = \frac{1}{\binom{140}{10}} \binom{50}{x} \binom{30}{z} \binom{60}{10 - x - z}\) for\(x + z \le 10\).
- \((Y, Z)\)tiene PDF\(f_{2,3}\) dado por\(f_{2,3}(y, z) = \frac{1}{\binom{140}{10}} \binom{40}{y} \binom{30}{z} \binom{70}{10 - y - z}\) for\(y + z \le 10\).
-
- \(X\)tiene PDF\(f_1\) dado por\(f_1(x) = \frac{1}{\binom{120}{10}} \binom{50}{x} \binom{90}{10 - x}\) for\(x \le 10\).
- \(Y\)tiene PDF\(f_2\) dado por\(f_2(y) = \frac{1}{\binom{120}{10}} \binom{40}{y} \binom{100}{10 - y}\) for\(y \le 10\).
- \(Z\)tiene PDF\(f_3\) dado por\(f_3(z) = \frac{1}{\binom{120}{10}} \binom{30}{z} \binom{110}{10 - z}\) para\(z \le 10\)
Ensayos Multinomiales
Supongamos que tenemos una secuencia de ensayos\(n\) independientes, cada uno con 4 posibles resultados. En cada ensayo, el resultado 1 ocurre con probabilidad\(p\), el resultado 2 con probabilidad\(q\), el resultado 3 con probabilidad\(r\) y el resultado 0 ocurre con probabilidad\(1 - p - q - r\). Los parámetros\(p\),\(q\), y\(r\) son números no negativos con\(p + q + r \le 1\), y\(n \in \N_+\). Denotar el número de veces que el resultado 1, el resultado 2 y el resultado 3 ocurrieron en los\(n\) ensayos por\(X\)\(Y\), y\(Z\) respectivamente. Por supuesto, el número de veces que ocurre el resultado 0 es\(n - X - Y - Z\). En los problemas a continuación, las variables\(x\)\(y\),, y\(z\) toman valores\(\N\).
\((X, Y, Z)\)tiene una distribución multinomial con función de densidad de probabilidad\(f\) dada por\[f(x, y, z) = \binom{n}{x, \, y, \, z} p^x q^y r^z (1 - p - q - r)^{n - x - y - z}, \quad x + y + z \le n\]
Prueba
El coeficiente multinomial es el número de secuencias de longitud\( n \) con 1\( x \) tiempos ocurridos, 2\( y \) tiempos ocurridos, 3\( z \) tiempos ocurridos y 0\( n - x - y - z \) veces ocurridos. El resultado sigue entonces por la independencia.
\((X, Y)\)también tiene una distribución multinomial con la función de densidad de probabilidad\(g\) dada por\[g(x, y) = \binom{n}{x, \, y} p^x q^y (1 - p - q)^{n - x - y}, \quad x + y \le n\]
Prueba
Este resultado podría obtenerse del PDF conjunto anterior, sumando\( z \) para fijo\( (x, y) \). Sin embargo hay un argumento directo mucho mejor. Tenga en cuenta que tenemos ensayos\(n\) independientes, y en cada ensayo, el resultado 1 ocurre con probabilidad\(p\), el resultado 2 con probabilidad\(q\) y algún otro resultado con probabilidad\(1 - p - q\).
\(X\)tiene una distribución binomial, con la función de densidad de probabilidad\(h\) dada por\[h(x) = \binom{n}{x} p^x (1 - p)^{n - x}, \quad x \le n\]
Prueba
Nuevamente, el resultado podría obtenerse sumando el PDF conjunto para\( (X, Y, Z) \) más\( (y, z) \) para fijo\( x \) o sumando el PDF conjunto para\( (X, Y) \) más\( y \) para fijo\( x \). Pero como antes, hay un argumento directo mucho mejor. Tenga en cuenta que tenemos ensayos\(n\) independientes, y en cada ensayo, el resultado 1 ocurre con probabilidad\(p\) y algún otro resultado con probabilidad\(1 - p\).
Estos resultados se generalizan de una manera completamente sencilla a ensayos multinomiales con cualquier número de resultados de ensayos. En resumen, si un vector aleatorio tiene una distribución multinomial, entonces cualquier subvector también tiene una distribución multinomial. En otros términos, todas las distribuciones marginales de una distribución multinomial son en sí mismas multinomiales. La distribución binomial y la distribución multinomial se estudian con más detalle en el capítulo de Ensayos de Bernoulli.
Supongamos que un sistema consta de 10 componentes que operan de forma independiente. Cada componente está trabajando con probabilidad\(\frac{1}{2}\), inactivo con probabilidad\(\frac{1}{3}\), o falló con probabilidad\(\frac{1}{6}\). Dejar\(X\) denotar el número de componentes de trabajo y\(Y\) el número de componentes inactivos. Dar la función de densidad de probabilidad de cada uno de los siguientes:
- \((X, Y)\)
- \(X\)
- \(Y\)
Contestar
En las fórmulas siguientes, las variables\(x\) y\(y\) son enteros no negativos.
- \((X, Y)\)tiene PDF\(f\) dado por\(f(x, y) = \binom{10}{x, \; y} \left(\frac{1}{2}\right)^x \left(\frac{1}{3}\right)^y \left(\frac{1}{6}\right)^{10 - x - y}\) for\(x + y \le 10\).
- \(X\)tiene PDF\(g\) dado por\(g(x) = \binom{10}{x} \left(\frac{1}{2}\right)^{10}\) for\(x \le 10\).
- \(Y\)tiene PDF\(h\) dado por\(h(y) = \binom{10}{y} \left(\frac{1}{3}\right)^y \left(\frac{2}{3}\right)^{10 - y}\) for\(y \le 10\).
Supongamos que en un dado torcido, de cuatro lados, la cara\(i\) ocurre con probabilidad\(\frac{i}{10}\) para\(i \in \{1, 2, 3, 4\}\). El dado se lanza 12 veces; vamos a\(X\) denotar el número de veces que se produce la puntuación 1,\(Y\) el número de veces que se produce la puntuación 2, y\(Z\) el número de veces que se produce la puntuación 3.
- Encuentra la función de densidad de probabilidad de\((X, Y, Z)\)
- Encuentra la función de densidad de probabilidad de cada par de variables.
- Encuentra la función de densidad de probabilidad de cada variable individual.
Contestar
En las fórmulas para los PDF a continuación, las variables\(x\),\(y\) y\(z\) son números enteros no negativos.
- \((X, Y, Z)\)tiene PDF\(f given by \(f(x, y, z) = \binom{12}{x, \, y, \, z} \left(\frac{1}{10}\right)^x \left(\frac{2}{10}\right)^y \left(\frac{3}{10}\right)^z \left(\frac{4}{10}\right)^{12 - x - y - z}\),\(x + y + z \le 12\)
-
- \((X, Y)\)tiene PDF\(f_{1,2}\) dado por\(f_{1,2}(x, y) = \binom{12}{x, \; y} \left(\frac{1}{10}\right)^{x} \left(\frac{2}{10}\right)^y \left(\frac{7}{10}\right)^{12 - x - y}\) for\(x + y \le 12\).
- \((X, Z)\)tiene PDF\(f_{1,3}\) dado por\(f_{1,3}(x, z) = \binom{12}{x, \; z} \left(\frac{1}{10}\right)^{x} \left(\frac{3}{10}\right)^z \left(\frac{6}{10}\right)^{12 - x - z}\) for\(x + z \le 12\).
- \((Y, Z)\)tiene PDF\(f_{2,3}\) dado por\(f_{2,3}(y, z) = \binom{12}{y, \; z} \left(\frac{2}{10}\right)^{y} \left(\frac{3}{10}\right)^z \left(\frac{5}{10}\right)^{12 - y - z}\) for\(y + z \le 12\).
-
- \(X\)tiene PDF\(f_1\) dado por\(f_1(x) = \binom{12}{x} \left(\frac{1}{10}\right)^x \left(\frac{9}{10}\right)^{12 - x}\) for\(x \le 12\).
- \(Y\)tiene PDF\(f_2\) dado por\(f_2(y) = \binom{12}{y} \left(\frac{2}{10}\right)^y \left(\frac{8}{10}\right)^{12 - y}\) for\(y \le 12\).
- \(Z\)tiene PDF\(f_3\) dado por\(f_3(z) = \binom{12}{z} \left(\frac{3}{10}\right)^z \left(\frac{7}{10}\right)^{12 - z}\) for\(z \le 12\).
Distribuciones normales bivariadas
Supongamos que\((X, Y)\) tiene probabilidad la función de densidad\(f\) dada a continuación:\[f(x, y) = \frac{1}{12 \pi} \exp\left[-\left(\frac{x^2}{8} + \frac{y^2}{18}\right)\right], \quad (x, y) \in \R^2\]
- Encuentra la función de densidad de probabilidad de\(X\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(X\)tiene PDF\(g\) dado por\(g(x) = \frac{1}{2 \sqrt{2 \pi}} e^{-x^2 / 8}\) for\(x \in \R\).
- \(Y\)tiene PDF\(h\) dado por\(h(y) = \frac{1}{3 \sqrt{2 \pi}} e^{-y^2 /18}\) for\(y \in \R\).
- \(X\)y\(Y\) son independientes.
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f\) dada a continuación:
\[f(x, y) = \frac{1}{\sqrt{3} \pi} \exp\left[-\frac{2}{3}\left(x^2 - x y + y^2\right)\right], \quad(x, y) \in \R^2\]- Encuentra la función de densidad de\(X\).
- Encuentra la función de densidad de\(Y\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(X\)tiene PDF\(g\) dado por\(g(x) = \frac{1}{\sqrt{2 \pi}} e^{-x^2 / 2}\) for\(x \in \R\).
- \(Y\)tiene PDF\(h\) dado por\(h(y) = \frac{1}{\sqrt{2 \pi}} e^{-y^2 / 2}\) for\(y \in \R\).
- \(X\)y\(Y\) son dependientes.
Las distribuciones conjuntas en los dos últimos ejercicios son ejemplos de distribuciones normales bivariadas. Las distribuciones normales son ampliamente utilizadas para modelar mediciones físicas sujetas a pequeños errores aleatorios. En ambos ejercicios, las distribuciones marginales de\( X \) y\( Y \) también tienen distribuciones normales, y esto resulta ser cierto en general. La distribución normal multivariada se estudia con más detalle en el capítulo sobre Distribuciones Especiales.
Distribuciones Exponenciales
Recordemos que la distribución exponencial tiene función de densidad de probabilidad\[f(x) = r e^{-r t}, \quad x \in [0, \infty)\] donde\(r \in (0, \infty)\) está el parámetro de tasa. La distribución exponencial es ampliamente utilizada para modelar tiempos aleatorios, y se estudia con más detalle en el capítulo sobre el Proceso de Poisson.
Supongamos\(X\) y\(Y\) tienen distribuciones exponenciales con parámetros\(a \in (0, \infty)\) y\(b \in (0, \infty)\), respectivamente, y son independientes. Entonces\(\P(X \lt Y) = \frac{a}{a + b}\).
Supongamos\(X\)\(Y\),, y\(Z\) tienen distribuciones exponenciales con parámetros\(a \in (0, \infty)\),\(b \in (0, \infty)\), y\(c \in (0, \infty)\), respectivamente, y son independientes. Entonces
- \(\P(X \lt Y \lt Z) = \frac{a}{a + b + c} \frac{b}{b + c}\)
- \(\P(X \lt Y, X \lt Z) = \frac{a}{a + b + c}\)
Si\(X\),\(Y\), y\(Z\) son las vidas de los dispositivos que actúan de manera independiente, entonces los resultados en los dos ejercicios anteriores dan probabilidades de diversas órdenes de falla. Los resultados de este tipo también son muy importantes en el estudio de los procesos de Markov en tiempo continuo. Continuaremos esta discusión en la sección sobre transformaciones de variables aleatorias.
Coordenadas Mixtas
Supongamos que\(X\) toma valores en el conjunto finito\(\{1, 2, 3\}\),\(Y\) toma valores en el intervalo\([0, 3]\), y que\((X, Y)\) tiene la función de densidad de probabilidad\(f\) dada por\[f(x, y) = \begin{cases} \frac{1}{3}, & \quad x = 1, \; 0 \le y \le 1 \\ \frac{1}{6}, & \quad x = 2, \; 0 \le y \le 2 \\ \frac{1}{9}, & \quad x = 3, \; 0 \le y \le 3 \end{cases}\]
- Encuentra la función de densidad de probabilidad de\(X\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(X\)tiene PDF\(g\) dado por\(g(x) = \frac{1}{3}\) for\(x \in \{1, 2, 3\}\) (la distribución uniforme en\(\{1, 2, 3\}\)).
- \(Y\)tiene PDF\(h\) dado por\(h(y) = \begin{cases} \frac{11}{18}, & 0 \lt y \lt 1 \\ \frac{5}{18}, & 1 \lt y \lt 2 \\ \frac{2}{18}, & 2 \lt y \lt 3 \end{cases}\).
- \(X\)y\(Y\) son dependientes.
Supongamos que\(P\) toma valores en el intervalo\([0, 1]\),\(X\) toma valores en el conjunto finito\(\{0, 1, 2, 3\}\), y que\((P, X)\) tiene la función de densidad de probabilidad\(f\) dada por\[f(p, x) = 6 \binom{3}{x} p^{x + 1} (1 - p)^{4 - x}, \quad (p, x) \in [0, 1] \times \{0, 1, 2, 3\}\]
- Encuentra la función de densidad de probabilidad de\(P\).
- Encuentra la función de densidad de probabilidad de\(X\).
- ¿Son\(P\) e\(X\) independientes?
Contestar
- \(P\)tiene PDF\(g\) dado por\(g(p) = 6 p (1 - p)\) for\(0 \le p \le 1\).
- \(X\)tiene PDF\(h\) dado por\( h(0) = h(3) = \frac{1}{5} \),\( h(1) = \frac{3}{10} \)
- \(P\)y\(X\) son dependientes.
Como veremos en la sección sobre distribuciones condicionales, la distribución en el último ejercicio modela el siguiente experimento:\(P\) se selecciona una probabilidad aleatoria, y luego una moneda con esta probabilidad de cabezas se arroja 3 veces;\(X\) es el número de cabezas. Tenga en cuenta que\( P \) tiene una distribución beta.
Muestras Aleatorias
Recordemos que la distribución de Bernoulli con parámetro\(p \in [0, 1]\) tiene función de densidad de probabilidad\(g\) dada por\(g(x) = p^x (1 - p)^{1 - x}\) for\(x \in \{0, 1\}\). Dejar\(\bs X = (X_1, X_2, \ldots, X_n)\) ser una muestra aleatoria de tamaño\(n \in \N_+\) a partir de la distribución. Dar la densidad de probabilidad funcion\(\bs X\) de forma simplificada.
Contestar
\(\bs X\)tiene PDF\(f\) dado por\(f(x_1, x_2, \ldots, x_n) = p^y (1 - p)^{n-y}\) for\((x_1, x_2, \ldots, x_n) \in \{0, 1\}^n\), donde\(y = x_1 + x_2 + \cdots + x_n\)
La distribución de Bernoulli es el nombre de Jacob Bernoulli, y gobierna un indicador varible aleatorio. De ahí\(\bs X\) que si es una muestra aleatoria de tamaño\(n\) de la distribución entonces\(\bs X\) es una secuencia de ensayos de\(n\) Bernoulli. Un capítulo aparte estudia con más detalle los ensayos de Bernoulli.
Recordemos que la distribución geométrica on\(\N_+\) con parámetro\(p \in (0, 1)\) tiene función de densidad de probabilidad\(g\) dada por\(g(x) = p (1 - p)^{x - 1}\) for\(x \in \N_+\). Dejar\(\bs X = (X_1, X_2, \ldots, X_n)\) ser una muestra aleatoria de tamaño\(n \in \N_+\) a partir de la distribución. Dar la función de densidad de probabilidad\(\bs X\) de forma simplificada.
Contestar
\(\bs X\)tiene pdf\(f\) dado por\(f(x_1, x_2, \ldots, x_n) = p^n (1 - p)^{y-n}\) for\((x_1, x_2, \ldots, x_n) \in \N_+^n\), donde\(y = x_1 + x_2 + \cdots + x_n\).
La distribución geométrica gobierna el número de prueba del primer éxito en una secuencia de ensayos de Bernoulli. De ahí que las variables en la muestra aleatoria puedan interpretarse como el número de ensayos entre éxitos sucesivos.
Recordemos que la distribución de Poisson con parámetro\(a \in (0, \infty)\) tiene la función de densidad de probabilidad\(g\) dada por\(g(x) = e^{-a} \frac{a^x}{x!}\) for\(x \in \N\). Dejar\(\bs X = (X_1, X_2, \ldots, X_n)\) ser una muestra aleatoria de tamaño\(n \in \N_+\) a partir de la distribución. Dar la densidad de probabilidad funcion\(\bs X\) de forma simplificada.
Contestar
\(\bs X\)tiene PDF\(f\) dado por\(f(x_1, x_2, \ldots, x_n) = \frac{1}{x_1! x_2! \cdots x_n!} e^{-n a} a^y\) for\((x_1, x_2, \ldots, x_n) \in \N^n\), donde\(y = x_1 + x_2 + \cdots + x_n\).
La distribución de Poisson lleva el nombre de Simeon Poisson, y gobierna el número de puntos aleatorios en una región de tiempo o espacio en circunstancias apropiadas. El parámetro\( a \) es proporcional al tamaño de la región. La distribución de Poisson se estudia con más detalle en el capítulo sobre el proceso de Poisson.
Recordemos nuevamente que la distribución exponencial con parámetro de tasa\(r \in (0, \infty)\) tiene función de densidad de probabilidad\(g\) dada por\(g(x) = r e^{-r x}\) for\(x \in (0, \infty)\). Dejar\(\bs X = (X_1, X_2, \ldots, X_n)\) ser una muestra aleatoria de tamaño\(n \in \N_+\) a partir de la distribución. Dar la densidad de probabilidad funcion\(\bs X\) de forma simplificada.
Contestar
\(\bs X\)tiene PDF\(f\) dado por\(f(x_1, x_2, \ldots, x_n) = r^n e^{-r y}\) for\((x_1, x_2, \ldots, x_n) \in [0, \infty)^n\), donde\(y = x_1 + x_2 + \cdots + x_n\).
La distribución exponencial rige los tiempos de falla y otros tipos o tiempos de llegada en las circunstancias apropiadas. La distribución exponencial se estudia con más detalle en el capítulo sobre el proceso de Poisson. Las variables en la muestra aleatoria pueden interpretarse como los tiempos entre llegadas sucesivas en el proceso de Poisson.
Recordemos que la distribución normal estándar tiene función de densidad de probabilidad\(\phi\) dada por\(\phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-z^2 / 2}\) for\(z \in \R\). Dejar\(\bs Z = (Z_1, Z_2, \ldots, Z_n)\) ser una muestra aleatoria de tamaño\(n \in \N_+\) a partir de la distribución. Dar la densidad de probabilidad funcion\(\bs Z\) de forma simplificada.
Contestar
\(\bs Z\)tiene PDF\(f\) dado por\(f(z_1, z_2, \ldots, z_n) = \frac{1}{(2 \pi)^{n/2}} e^{-\frac{1}{2} w^2}\) for\((z_1, z_2, \ldots, z_n) \in \R^n\), donde\(w^2 = z_1^2 + z_2^2 + \cdots + z_n^2\).
La distribución normal estándar gobierna las cantidades físicas, adecuadamente escaladas y centradas, sujetas a pequeños errores aleatorios. La distribución normal se estudia en mayor generalidad en el capítulo sobre las Distribuciones Especiales.
Ejercicios de Análisis de Datos
Para los datos de cigarra,\(G\) denota género y\(S\) denota tipo de especie.
- Encuentra la densidad empírica de\((G, S)\).
- Encuentra la densidad empírica de\(G\).
- Encuentra la densidad empírica de\(S\).
- ¿Crees eso\(S\) y\(G\) eres independiente?
Contestar
Las densidades empíricas articulares y marginales se dan en la siguiente tabla. El género y las especies son probablemente dependientes (comparar la densidad articular con el producto de las densidades marginales).
| \(f(i, j)\) | \(i = 0\) | 1 | \(h(j)\) |
|---|---|---|---|
| \(j = 0\) | \(\frac{16}{104}\) | \(\frac{28}{104}\) | \(\frac{44}{104}\) |
| 1 | \(\frac{3}{104}\) | \(\frac{3}{104}\) | \(\frac{6}{104}\) |
| 2 | \(\frac{40}{104}\) | \(\frac{14}{104}\) | \(\frac{56}{104}\) |
| \(g(i)\) | \(\frac{59}{104}\) | \(\frac{45}{104}\) | 1 |
Para los datos de cigarra, vamos a\(W\) denotar peso corporal (en gramos) y longitud\(L\) corporal (en milímetros).
- Construir una densidad empírica para\((W, L)\).
- Encuentra la densidad empírica correspondiente para\(W\).
- Encuentra la densidad empírica correspondiente para\(L\).
- ¿Crees eso\(W\) y\(L\) eres independiente?
Contestar
Las densidades empíricas articulares y marginales, basadas en particiones simples de los rangos de peso corporal y longitud corporal, se dan en la siguiente tabla. El peso corporal y la longitud corporal son casi con certeza dependientes.
| Densidad\((W, L)\) | \(w \in (0, 0.1]\) | \((0.1, 0.2]\) | \((0.2, 0.3]\) | \((0.3, 0.4]\) | Densidad\(L\) |
|---|---|---|---|---|---|
| \(l \in (15, 20]\) | 0 | 0.0385 | 0.0192 | 0 | 0.0058 |
| \((20, 25]\) | 0.1731 | 0.9808 | 0.4231 | 0 | 0.1577 |
| \((25, 30]\) | 0 | 0.1538 | 0.1731 | 0.0192 | 0.0346 |
| \((30, 35]\) | 0 | 0 | 0 | 0.0192 | 0.0019 |
| Densidad\(W\) | 0.8654 | 5.8654 | 3.0769 | 0.1923 |
Para los datos de cigarra, vamos a\(G\) denotar género y peso\(W\) corporal (en gramos).
- Constructo y densidad empírica para\((W, G)\).
- Encuentra la densidad empírica para\(G\).
- Encuentra la densidad empírica para\(W\).
- ¿Crees eso\(G\) y\(W\) eres independiente?
Responder
Las densidades empíricas articulares y marginales, basadas en una simple partición del rango de peso corporal, se dan en la siguiente tabla. El peso corporal y el género son casi con certeza dependientes.
| Densidad\((W, G)\) | \(w \in (0, 0.1]\) | \((0.1, 0.2]\) | \((0.2, 0.3]\) | \((0.3, 0.4]\) | Densidad\(G\) |
|---|---|---|---|---|---|
| \(g = 0\) | 0.1923 | 2.5000 | 2.8846 | 0.0962 | 0.5673 |
| 1 | 0.6731 | 3.3654 | 0.1923 | 0.0962 | 0.4327 |
| Densidad\(W\) | 0.8654 | 5.8654 | 3.0769 | 0.1923 |


