3.7: Transformaciones de variables aleatorias
- Page ID
- 151561
En esta sección se estudia cómo cambia la distribución de una variable aleatoria cuando la variable se transfomora de manera determinista. Si eres un nuevo estudiante de probabilidad, debes saltarte los detalles técnicos.
Teoría Básica
EL PROBLEMA
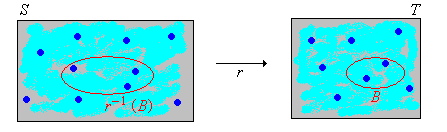
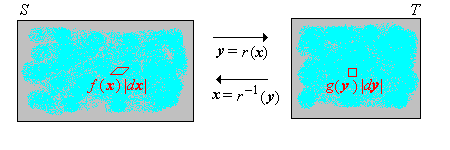
Como es habitual, comenzamos con un experimento aleatorio modelado por un espacio de probabilidad\((\Omega, \mathscr F, \P)\). Entonces, para revisar,\(\Omega\) es el conjunto de resultados,\(\mathscr F\) es la colección de eventos, y\(\P\) es la medida de probabilidad en el espacio muestral\( (\Omega, \mathscr F) \). Supongamos ahora que tenemos una variable aleatoria\(X\) para el experimento, tomando valores en un conjunto\(S\), y una función\(r\) de\( S \) en otro conjunto\( T \). Entonces\(Y = r(X)\) es una nueva variable aleatoria tomando valores en\(T\). Si\(X\) se conoce la distribución de, ¿cómo encontramos la distribución de\(Y\)? Esta es una pregunta muy básica e importante, y en un sentido superficial, la solución es fácil. Pero primero recordemos que para\( B \subseteq T \),\(r^{-1}(B) = \{x \in S: r(x) \in B\}\) es la imagen inversa de\(B\) bajo\(r\).
\(\P(Y \in B) = \P\left[X \in r^{-1}(B)\right]\)para\(B \subseteq T\).
Prueba
Sin embargo, frecuentemente la distribución de\(X\) se conoce ya sea a través de su función de distribución\(F\) o su función de densidad de probabilidad\(f\), y de manera similar nos gustaría encontrar la función de distribución o la función de densidad de probabilidad de\(Y\). Este es un problema difícil en general, porque como veremos, incluso transformaciones simples de variables con distribuciones simples pueden conducir a variables con distribuciones complejas. Vamos a resolver el problema en diversos casos especiales.
Variables transformadas con distribuciones discretas
Cuando la variable transformada\(Y\) tiene una distribución discreta, la función de densidad de probabilidad de\(Y\) puede calcularse usando reglas básicas de probabilidad.
Supongamos que\(X\) tiene una distribución discreta en un conjunto contable\(S\), con función de densidad de probabilidad\(f\). Luego\(Y\) tiene una distribución discreta con función de densidad de probabilidad\(g\) dada por\[ g(y) = \sum_{x \in r^{-1}\{y\}} f(x), \quad y \in T \]
Prueba
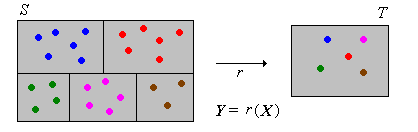
Supongamos que\(X\) tiene una distribución continua en un subconjunto\(S \subseteq \R^n\) con función de densidad de probabilidad\(f\), y que\(T\) es contable. Luego\(Y\) tiene una distribución discreta con función de densidad de probabilidad\(g\) dada por\[ g(y) = \int_{r^{-1}\{y\}} f(x) \, dx, \quad y \in T \]
Prueba
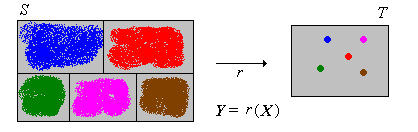
Entonces el principal problema suele ser computar las imágenes inversas\(r^{-1}\{y\}\) para\(y \in T\). No vale la pena memorizar explícitamente las fórmulas anteriores en los casos discretos y continuos; generalmente es mejor trabajar cada problema desde cero. El paso principal es escribir el evento\(\{Y = y\}\) en términos de\(X\), y luego encontrar la probabilidad de este evento usando la función de densidad de probabilidad de\( X \).
Variables transformadas con distribuciones continuas
Supongamos que\(X\) tiene una distribución continua en un subconjunto\(S \subseteq \R^n\) y que\(Y = r(X)\) tiene una distribución continua en un subconjunto\(T \subseteq \R^m\). Supongamos también que\(X\) tiene una función de densidad de probabilidad conocida\(f\). En muchos casos, la función de densidad de probabilidad de se\(Y\) puede encontrar primero encontrando la función de distribución de\(Y\) (usando reglas básicas de probabilidad) y luego calculando las derivadas apropiadas de la función de distribución. Este método general se denomina, apropiadamente, como el método de función de distribución.
Supongamos que\(Y\) es real valorado. La función\(G\) de distribución de\(Y\) viene dada por
\[ G(y) = \int_{r^{-1}(-\infty, y]} f(x) \, dx, \quad y \in \R \]Prueba
Nuevamente, esto se desprende de la definición de\(f\) como PDF de\(X\). Para\( y \in \R \),\[ G(y) = \P(Y \le y) = \P\left[r(X) \in (-\infty, y]\right] = \P\left[X \in r^{-1}(-\infty, y]\right] = \int_{r^{-1}(-\infty, y]} f(x) \, dx \]
Como en el caso discreto, la fórmula en (4) no ayuda mucho, y suele ser mejor trabajar cada problema desde cero. El paso principal es escribir el evento\(\{Y \le y\}\) en términos de\(X\), y luego encontrar la probabilidad de este evento usando la función de densidad de probabilidad de\( X \).
La fórmula del cambio de variables
Cuando la transformación\(r\) es uno a uno y suave, hay una fórmula para la función de densidad de probabilidad de\(Y\) directamente en términos de la función de densidad de probabilidad de\(X\). Esto se conoce como fórmula de cambio de variables. Tenga en cuenta que dado que\(r\) es uno a uno, tiene una función inversa\(r^{-1}\).
Exploraremos primero el caso unidimensional, donde los conceptos y fórmulas son más simples. Así, supongamos que la variable aleatoria\(X\) tiene una distribución continua en un intervalo\(S \subseteq \R\), con función de distribución\(F\) y función de densidad de probabilidad\(f\). Supongamos que\(Y = r(X)\) donde\(r\) es una función diferenciable de\(S\) sobre un intervalo\(T\). Como de costumbre, vamos a dejar\(G\) denotar la función de distribución de\(Y\) y\(g\) la función de densidad de probabilidad de\(Y\).
Supongamos que\(r\) está aumentando estrictamente en\(S\). Para\(y \in T\),
- \(G(y) = F\left[r^{-1}(y)\right]\)
- \(g(y) = f\left[r^{-1}(y)\right] \frac{d}{dy} r^{-1}(y)\)
Prueba
- \( G(y) = \P(Y \le y) = \P[r(X) \le y] = \P\left[X \le r^{-1}(y)\right] = F\left[r^{-1}(y)\right] \)para\( y \in T \). Tenga en cuenta que la incalidad se conserva ya que\( r \) va en aumento.
- Esto se desprende de la parte (a) tomando derivados con respecto\( y \) y utilizando la regla de la cadena. Recordemos eso\( F^\prime = f \).
Supongamos que\(r\) es estrictamente decreciente en\(S\). Para\(y \in T\),
- \(G(y) = 1 - F\left[r^{-1}(y)\right]\)
- \(g(y) = -f\left[r^{-1}(y)\right] \frac{d}{dy} r^{-1}(y)\)
Prueba
- \( G(y) = \P(Y \le y) = \P[r(X) \le y] = \P\left[X \ge r^{-1}(y)\right] = 1 - F\left[r^{-1}(y)\right] \)para\( y \in T \). Tenga en cuenta que la incalidad se invierte ya que\( r \) es decreciente.
- Esto se desprende de la parte (a) tomando derivados con respecto\( y \) y utilizando la regla de la cadena. Recordemos de nuevo eso\( F^\prime = f \).
Las fórmulas para las funciones de densidad de probabilidad en el caso creciente y el caso decreciente se pueden combinar:
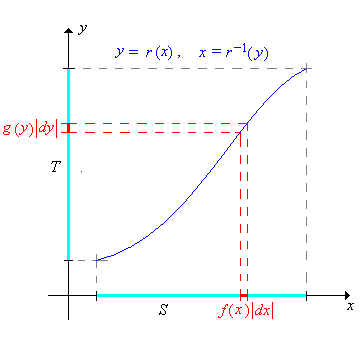
Si\(r\) es estrictamente creciente o estrictamente decreciente\(S\) entonces la función\(g\) de densidad de probabilidad de\(Y\) viene dada por\[ g(y) = f\left[ r^{-1}(y) \right] \left| \frac{d}{dy} r^{-1}(y) \right| \]
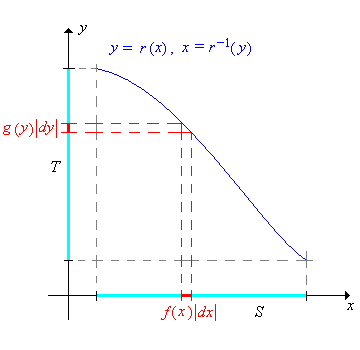
Dejando\(x = r^{-1}(y)\), el cambio de variables de fórmula se puede escribir de manera más compacta como\[ g(y) = f(x) \left| \frac{dx}{dy} \right| \] Aunque sucinta y fácil de recordar, la fórmula es un poco menos clara. Debe entenderse que a la\(x\) derecha debe escribirse en términos de\(y\) vía la función inversa. Las siguientes imágenes dan una interpretación gráfica de la fórmula en los dos casos donde\(r\) está aumentando y donde\(r\) está disminuyendo.
La generalización de este resultado de\( \R \) a\( \R^n \) es básicamente un teorema en el cálculo multivariado. Primero necesitamos alguna notación. Supongamos que\( r \) es una función diferenciable uno a uno de\( S \subseteq \R^n \) hacia\( T \subseteq \R^n \). La primera derivada de la función inversa\(\bs x = r^{-1}(\bs y)\) es la\(n \times n\) matriz de primeras derivadas parciales:\[ \left( \frac{d \bs x}{d \bs y} \right)_{i j} = \frac{\partial x_i}{\partial y_j} \] El jacobiano (nombrado en honor a Karl Gustav Jacobi) de la función inversa es el determinante de la primera matriz derivada\[ \det \left( \frac{d \bs x}{d \bs y} \right) \] Con este compacto notación, la fórmula de cambio multivariado de variables es fácil de declarar.
Supongamos que\(\bs X\) es una variable aleatoria que toma valores\(S \subseteq \R^n\), y que\(\bs X\) tiene una distribución continua con función de densidad de probabilidad\(f\). Supongamos también\( Y = r(X) \) dónde\( r \) es una función diferenciable de\( S \) hacia\( T \subseteq \R^n \). Entonces la función de densidad de probabilidad\(g\) de\(\bs Y\) viene dada por\[ g(\bs y) = f(\bs x) \left| \det \left( \frac{d \bs x}{d \bs y} \right) \right|, \quad y \in T \]
Prueba
El resultado se desprende de la fórmula de cambio multivariado de variables en cálculo. Si\(B \subseteq T\) entonces\[\P(\bs Y \in B) = \P[r(\bs X) \in B] = \P[\bs X \in r^{-1}(B)] = \int_{r^{-1}(B)} f(\bs x) \, d\bs x\] Usando el cambio de variables\(\bs x = r^{-1}(\bs y)\),\(d\bs x = \left|\det \left( \frac{d \bs x}{d \bs y} \right)\right|\, d\bs y\) tenemos\[\P(\bs Y \in B) = \int_B f[r^{-1}(\bs y)] \left|\det \left( \frac{d \bs x}{d \bs y} \right)\right|\, d \bs y\] Así se deduce que\(g\) se define en el teorema es un PDF para\(\bs Y\).
El jacobiano es el factor de escala infinitesimal que describe cómo cambia el volumen\(n\) -dimensional bajo la transformación.
Transformaciones especiales
Transformaciones Lineales
Las transformaciones lineales (o transformaciones más afines técnicamente) se encuentran entre las transformaciones más comunes e importantes. Además, este tipo de transformación conduce a aplicaciones simples del cambio de teoremas de variables. Supongamos primero que\(X\) es una variable aleatoria que toma valores en un intervalo\(S \subseteq \R\) y que\(X\) tiene una distribución continua\(S\) con función de densidad de probabilidad\(f\). Dejemos\(Y = a + b \, X\) dónde\(a \in \R\) y\(b \in \R \setminus\{0\}\). Tenga en cuenta que\(Y\) toma valores en\(T = \{y = a + b x: x \in S\}\), que también es un intervalo.
\(Y\)tiene función de densidad de probabilidad\( g \) dada por\[ g(y) = \frac{1}{\left|b\right|} f\left(\frac{y - a}{b}\right), \quad y \in T \]
Prueba
La transformación es\( y = a + b \, x \). De ahí que la transformación inversa sea\( x = (y - a) / b \) y\( dx / dy = 1 / b \). El resultado ahora se desprende del teorema del cambio de variables.
Cuando\(b \gt 0\) (que suele ser el caso en las aplicaciones), esta transformación se conoce como transformación a escala de ubicación;\(a\) es el parámetro de ubicación y\(b\) es el parámetro de escala. Las transformaciones de escala surgen naturalmente cuando se cambian las unidades físicas (de pies a metros, por ejemplo). Las transformaciones de ubicación surgen naturalmente cuando se cambia el punto de referencia físico (midiendo el tiempo relativo a las 9:00 AM en lugar de las 8:00 AM, por ejemplo). El cambio de medición de temperatura de Fahrenheit a Celsius es una transformación de ubicación y escala. Las transformaciones a escala de ubicación se estudian con más detalle en el capítulo sobre Distribuciones Especiales.
La versión multivariada de este resultado tiene una forma simple y elegante cuando la transformación lineal se expresa en forma matriz-vector. Por lo tanto, supongamos que\(\bs X\) es una variable aleatoria que toma valores\(S \subseteq \R^n\) y que\(\bs X\) tiene una distribución continua\(S\) con función de densidad de probabilidad\(f\). Vamos\(\bs Y = \bs a + \bs B \bs X\) donde\(\bs a \in \R^n\) y\(\bs B\) es una\(n \times n\) matriz invertible. Tenga en cuenta que\(\bs Y\) toma valores en\(T = \{\bs a + \bs B \bs x: \bs x \in S\} \subseteq \R^n\).
\(\bs Y\)tiene función de densidad de probabilidad\(g\) dada por\[ g(\bs y) = \frac{1}{\left| \det(\bs B)\right|} f\left[ B^{-1}(\bs y - \bs a) \right], \quad \bs y \in T \]
Prueba
La transformación\(\bs y = \bs a + \bs B \bs x\) mapea\(\R^n\) uno a uno y hacia\(\R^n\). La transformación inversa es\(\bs x = \bs B^{-1}(\bs y - \bs a)\). El jacobiano de la transformación inversa es la función constante\(\det (\bs B^{-1}) = 1 / \det(\bs B)\). El resultado ahora se desprende del teorema del cambio multivariado de variables.
Sumas y convolución
La simple adición de variables aleatorias es quizás la más importante de todas las transformaciones. Supongamos que\(X\) y\(Y\) son variables aleatorias en un espacio de probabilidad, tomando valores en\( R \subseteq \R\) y\( S \subseteq \R \), respectivamente, de modo que\( (X, Y) \) toma valores en un subconjunto de\( R \times S \). Nuestro objetivo es encontrar la distribución de\(Z = X + Y\). Tenga en cuenta que\( Z \) toma valores en\( T = \{z \in \R: z = x + y \text{ for some } x \in R, y \in S\} \). Para\( z \in T \), vamos\( D_z = \{x \in R: z - x \in S\} \).
Supongamos que función de densidad de\((X, Y)\) probabilidad\(f\).
- Si\( (X, Y) \) tiene una distribución discreta, entonces\(Z = X + Y\) tiene una distribución discreta con la función de densidad de probabilidad\(u\) dada por\[ u(z) = \sum_{x \in D_z} f(x, z - x), \quad z \in T \]
- Si\( (X, Y) \) tiene una distribución continua entonces\(Z = X + Y\) tiene una distribución continua con la función de densidad de probabilidad\(u\) dada por\[ u(z) = \int_{D_z} f(x, z - x) \, dx, \quad z \in T \]
Prueba
- \( \P(Z = z) = \P\left(X = x, Y = z - x \text{ for some } x \in D_z\right) = \sum_{x \in D_z} f(x, z - x) \)
- Para\( A \subseteq T \), vamos\( C = \{(u, v) \in R \times S: u + v \in A\} \). Entonces\[ \P(Z \in A) = \P(X + Y \in A) = \int_C f(u, v) \, d(u, v) \] Ahora usa el cambio de variables\( x = u, \; z = u + v \). Entonces la transformación inversa es\( u = x, \; v = z - x \) y el jacobiano es 1. Utilizando el teorema de cambio de variables (8) tenemos\[ \P(Z \in A) = \int_{D_z \times A} f(x, z - x) \, d(x, z) = \int_A \int_{D_z} f(x, z - x) \, dx \, dz \] Se deduce que\( Z \) tiene función de densidad de probabilidad\( z \mapsto \int_{D_z} f(x, z - x) \, dx \).
En el caso discreto,\( R \) y\( S \) son contables, por lo que también\( T \) es contable como es\( D_z \) para cada uno\( z \in T \). En el caso continuo,\( R \) y\( S \) suelen ser intervalos, por lo que también\( T \) es un intervalo como es\( D_z \) para\( z \in T \). En ambos casos, determinar\( D_z \) suele ser el paso más difícil. Con mucho, el caso especial más importante ocurre cuando\(X\) y\(Y\) son independientes.
Supongamos que\(X\) y\(Y\) son independientes y tienen funciones de densidad de probabilidad\(g\) y\(h\) respectivamente.
- Si\( X \) y\( Y \) tienen distribuciones discretas, entonces\( Z = X + Y \) tiene una distribución discreta con función de densidad de probabilidad\( g * h \) dada por\[ (g * h)(z) = \sum_{x \in D_z} g(x) h(z - x), \quad z \in T \]
- Si\( X \) y\( Y \) tienen distribuciones continuas entonces\( Z = X + Y \) tiene una distribución continua con la función de densidad de probabilidad\( g * h \) dada por\[ (g * h)(z) = \int_{D_z} g(x) h(z - x) \, dx, \quad z \in T \]
En ambos casos, la función de densidad de probabilidad\(g * h\) se denomina convolución de\(g\) y\(h\).
Prueba
Ambos resultados se deduce del resultado anterior ya que\( f(x, y) = g(x) h(y) \) es la función de densidad de probabilidad de\( (X, Y) \).
Como antes, determinar este conjunto\( D_z \) es a menudo el paso más desafiante para encontrar la función de densidad de probabilidad de\(Z\). Sin embargo, hay un caso en el que los cálculos simplifican significativamente.
Supongamos de nuevo que\( X \) y\( Y \) son variables aleatorias independientes con funciones de densidad de probabilidad\( g \) y\( h \), respectivamente.
- En el caso discreto, suponga\( X \) y\( Y \) toma valores\( \N \). Entonces\( Z \) tiene la función de densidad de probabilidad\[ (g * h)(z) = \sum_{x = 0}^z g(x) h(z - x), \quad z \in \N \]
- En el caso continuo, supongamos eso\( X \) y\( Y \) tomar valores adentro\( [0, \infty) \). Entonces\( Z \) y tiene función de densidad de probabilidad\[ (g * h)(z) = \int_0^z g(x) h(z - x) \, dx, \quad z \in [0, \infty) \]
Prueba
- En este caso,\( D_z = \{0, 1, \ldots, z\} \) para\( z \in \N \).
- En este caso,\( D_z = [0, z] \) para\( z \in [0, \infty) \).
La convolución es una operación matemática muy importante que ocurre en áreas de las matemáticas fuera de la probabilidad, y por lo tanto involucra funciones que no son necesariamente funciones de densidad de probabilidad. El siguiente resultado da algunas propiedades simples de convolución.
Convolución (ya sea discreta o continua) satisface las siguientes propiedades, donde\(f\),\(g\), y\(h\) son funciones de densidad de probabilidad del mismo tipo.
- \(f * g = g * f\)(la propiedad conmutativa)
- \((f * g) * h = f * (g * h)\)(la propiedad asociativa)
Prueba
Una prueba analítica es posible, basada en la definición de convolución, pero una prueba probabilística, basada en sumas de variables aleatorias independientes es mucho mejor. Así, supongamos que\( X \),\( Y \), y\( Z \) son variables aleatorias independientes con PDFs\( f \)\( g \),, y\( h \), respectivamente.
- La propiedad conmutativa de convolución se desprende de la propiedad conmutativa de adición:\( X + Y = Y + X \).
- La propiedad asociativa de convolución se desprende de la propiedad asociada de adición:\( (X + Y) + Z = X + (Y + Z) \).
Así, en la parte (b) podemos escribir\(f * g * h\) sin ambigüedades. Por supuesto, la constante 0 es la identidad aditiva así\( X + 0 = 0 + X = 0 \) para cada variable aleatoria\( X \). Además, una constante es independiente de cualquier otra variable aleatoria. De ello se deduce que la función\( \delta \) de densidad de probabilidad de 0 (dada por\( \delta(0) = 1 \)) es la identidad con respecto a la convolución (al menos para PDFs discretos). Es decir,\( f * \delta = \delta * f = f \). El siguiente resultado es un simple corolario del teorema de la convolución, pero es lo suficientemente importante como para ser destacado.
Supongamos que\(\bs X = (X_1, X_2, \ldots)\) es una secuencia de variables aleatorias independientes e idénticamente distribuidas de valor real, con función de densidad de probabilidad común\(f\). Entonces\(Y_n = X_1 + X_2 + \cdots + X_n\) tiene la función de densidad de probabilidad\(f^{*n} = f * f * \cdots * f \), el poder de convolución\(n\) -fold de\(f\), para\(n \in \N\).
En términos estadísticos,\( \bs X \) corresponde al muestreo de la distribución común.Por convención,\( Y_0 = 0 \), así que naturalmente tomamos\( f^{*0} = \delta \). Cuando se escala y se centra apropiadamente, la distribución de\(Y_n\) converge a la distribución normal estándar como\(n \to \infty\). La afirmación precisa de este resultado es el teorema del límite central, uno de los teoremas fundamentales de la probabilidad. El teorema del límite central se estudia en detalle en el capítulo sobre Muestras Aleatorias. Claramente el poder de convolución satisface la ley de los exponentes:\( f^{*n} * f^{*m} = f^{*(n + m)} \) para\( m, \; n \in \N \).
La convolución puede generalizarse a sumas de variables independientes que no son del mismo tipo, pero esta generalización se suele hacer en términos de funciones de distribución en lugar de funciones de densidad de probabilidad.
Productos y cocientes
Si bien no son tan importantes como las sumas, los productos y cocientes de las variables aleatorias de valor real también ocurren con frecuencia. Limitaremos nuestra discusión a distribuciones continuas.
Supongamos que\( (X, Y) \) tiene una distribución continua\( \R^2 \) con función de densidad de probabilidad\( f \).
- Variable aleatoria\( V = X Y \) tiene función de densidad de probabilidad\[ v \mapsto \int_{-\infty}^\infty f(x, v / x) \frac{1}{|x|} dx \]
- Variable aleatoria\( W = Y / X \) tiene función de densidad de probabilidad\[ w \mapsto \int_{-\infty}^\infty f(x, w x) |x| dx \]
Prueba
Introducimos la variable auxiliar\( U = X \) para que tengamos transformaciones bivariadas y podamos usar nuestra fórmula de cambio de variables.
- Tenemos la transformación\( u = x \),\( v = x y\) y así la transformación inversa es\( x = u \),\( y = v / u\). De ahí\[ \frac{\partial(x, y)}{\partial(u, v)} = \left[\begin{matrix} 1 & 0 \\ -v/u^2 & 1/u\end{matrix} \right] \] y así lo es el jacobiano\( 1/u \). Utilizando el teorema del cambio de variables, el PDF conjunto de\( (U, V) \) es\( (u, v) \mapsto f(u, v / u)|1 /|u| \). De ahí que el PDF de\( V \) es\[ v \mapsto \int_{-\infty}^\infty f(u, v / u) \frac{1}{|u|} du \]
- Tenemos la transformación\( u = x \),\( w = y / x \) y así la transformación inversa es\( x = u \),\( y = u w \). De ahí\[ \frac{\partial(x, y)}{\partial(u, w)} = \left[\begin{matrix} 1 & 0 \\ w & u\end{matrix} \right] \] y así lo es el jacobiano\( u \). Usando la fórmula de cambio de variables, el PDF conjunto de\( (U, W) \) es\( (u, w) \mapsto f(u, u w) |u| \). De ahí que el PDF de W sea\[ w \mapsto \int_{-\infty}^\infty f(u, u w) |u| du \]
Si\( (X, Y) \) toma valores en un subconjunto\( D \subseteq \R^2 \), entonces para un dado\( v \in \R \), la integral en (a) ha terminado\( \{x \in \R: (x, v / x) \in D\} \), y para un dado\( w \in \R \), la integral en (b) ha terminado\( \{x \in \R: (x, w x) \in D\} \). Como es habitual, el caso especial más importante de este resultado es cuándo\( X \) y\( Y \) son independientes.
Supongamos que\( X \) y\( Y \) son variables aleatorias independientes con distribuciones continuas al\( \R \) tener funciones de densidad de probabilidad\( g \) y\( h \), respectivamente.
- Variable aleatoria\( V = X Y \) tiene función de densidad de probabilidad\[ v \mapsto \int_{-\infty}^\infty g(x) h(v / x) \frac{1}{|x|} dx \]
- Variable aleatoria\( W = Y / X \) tiene función de densidad de probabilidad\[ w \mapsto \int_{-\infty}^\infty g(x) h(w x) |x| dx \]
Prueba
Estos resultados siguen inmediatamente del teorema anterior, ya que\( f(x, y) = g(x) h(y) \) para\( (x, y) \in \R^2 \).
Si\( X \) toma valores\( S \subseteq \R \) y\( Y \) toma valores en\( T \subseteq \R \), entonces para un dado\( v \in \R \), la integral en (a) ha terminado\( \{x \in S: v / x \in T\} \), y para un dado\( w \in \R \), la integral en (b) ha terminado\( \{x \in S: w x \in T\} \). Al igual que con la convolución, determinar el dominio de la integración suele ser el paso más desafiante.
Mínimo y Máximo
Supongamos que\((X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias independientes de valor real. Las transformaciones mínimas y máximas\[U = \min\{X_1, X_2, \ldots, X_n\}, \quad V = \max\{X_1, X_2, \ldots, X_n\} \] son muy importantes en una serie de aplicaciones. Por ejemplo, recordemos que en el modelo estándar de confiabilidad estructural, un sistema consiste en\(n\) componentes que operan de manera independiente. Supongamos que\(X_i\) representa la vida útil del componente\(i \in \{1, 2, \ldots, n\}\). Entonces\(U\) es la vida útil del sistema en serie que opera si y solo si cada componente está operando. Del mismo modo,\(V\) es la vida útil del sistema paralelo el que opera si y solo si al menos un componente está operando.
Un caso especial particularmente importante ocurre cuando las variables aleatorias se distribuyen de manera idéntica, además de ser independientes. En este caso, la secuencia de variables es una muestra aleatoria de tamaño\(n\) de la distribución común. Las variables mínima y máxima son los ejemplos extremos de las estadísticas de orden. Las estadísticas de orden se estudian en detalle en el capítulo sobre Muestras Aleatorias.
Supongamos que\((X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias indendientes de valor real y que\(X_i\) tiene función de distribución\(F_i\) para\(i \in \{1, 2, \ldots, n\}\).
- \(V = \max\{X_1, X_2, \ldots, X_n\}\)tiene función de distribución\(H\) dada por\(H(x) = F_1(x) F_2(x) \cdots F_n(x)\) for\(x \in \R\).
- \(U = \min\{X_1, X_2, \ldots, X_n\}\)tiene función de distribución\(G\) dada por\(G(x) = 1 - \left[1 - F_1(x)\right] \left[1 - F_2(x)\right] \cdots \left[1 - F_n(x)\right]\) for\(x \in \R\).
Prueba
- Tenga en cuenta que ya que\( V \) es el máximo de las variables,\(\{V \le x\} = \{X_1 \le x, X_2 \le x, \ldots, X_n \le x\}\). De ahí que por independencia,\[H(x) = \P(V \le x) = \P(X_1 \le x) \P(X_2 \le x) \cdots \P(X_n \le x) = F_1(x) F_2(x) \cdots F_n(x), \quad x \in \R\]
- Tenga en cuenta que\( U \) ya que como mínimo de las variables,\(\{U \gt x\} = \{X_1 \gt x, X_2 \gt x, \ldots, X_n \gt x\}\). De ahí que por independencia,\ comience {alinear*} G (x) & =\ P (U\ le x) = 1 -\ P (U\ gt x) = 1 -\ P (X_1\ gt x)\ P (X_2\ gt x)\ cdots P (x_n\ gt x)\\ & = 1 - [1 - F_1 (x)] [1 - F_2 (x)]\ cdots [1 - F_n (x)],\ quad x\ in\ R\ final {alinear*}
De la parte (a), tenga en cuenta que el producto de las funciones de\(n\) distribución es otra función de distribución. De la parte (b), el producto de las funciones de distribución de\(n\) cola derecha es una función de distribución de cola derecha. En el ajuste de confiabilidad, donde las variables aleatorias no son negativas, la última declaración significa que el producto de las funciones de\(n\) confiabilidad es otra función de confiabilidad. Si\(X_i\) tiene una distribución continua con función de densidad de probabilidad\(f_i\) para cada uno\(i \in \{1, 2, \ldots, n\}\), entonces\(U\) y\(V\) también tienen distribuciones continuas, y sus funciones de densidad de probabilidad se pueden obtener diferenciando las funciones de distribución en las partes (a) y (b) de último teorema. Los cálculos son sencillos usando la regla del producto para derivados, pero los resultados son un poco desordenados.
Las fórmulas en el último teorema son particularmente agradables cuando las variables aleatorias están distribuidas de manera idéntica, además de ser independientes
Supongamos que\((X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias independientes de valor real, con función de distribución común\(F\).
- \(V = \max\{X_1, X_2, \ldots, X_n\}\)tiene función de distribución\(H\) dada por\(H(x) = F^n(x)\) for\(x \in \R\).
- \(U = \min\{X_1, X_2, \ldots, X_n\}\)tiene función de distribución\(G\) dada por\(G(x) = 1 - \left[1 - F(x)\right]^n\) for\(x \in \R\).
En particular, se deduce que una potencia entera positiva de una función de distribución es una función de distribución. De manera más general, es fácil ver que cada potencia positiva de una función de distribución es una función de distribución. ¿Cómo podríamos construir una potencia no entera de una función de distribución de manera probabilística?
Supongamos que\((X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias independientes de valor real, con una distribución continua común que tiene función de densidad de probabilidad\(f\).
- \(V = \max\{X_1, X_2, \ldots, X_n\}\)tiene función de densidad de probabilidad\(h\) dada por\(h(x) = n F^{n-1}(x) f(x)\) for\(x \in \R\).
- \(U = \min\{X_1, X_2, \ldots, X_n\}\)tiene función de densidad de probabilidad\(g\) dada por\(g(x) = n\left[1 - F(x)\right]^{n-1} f(x)\) for\(x \in \R\).
Sistemas de coordenadas
Para nuestra próxima discusión, consideraremos transformaciones que corresponden a sistemas de coordenadas comunes basados en distancia-ángulo: coordenadas polares en el plano y coordenadas cilíndricas y esféricas en el espacio tridimensional. Primero, para\( (x, y) \in \R^2 \), vamos a\( (r, \theta) \) denotar las coordenadas polares estándar correspondientes a las coordenadas cartesianas\((x, y)\), de manera que esa\( r \in [0, \infty) \) es la distancia radial y\( \theta \in [0, 2 \pi) \) es el ángulo polar.
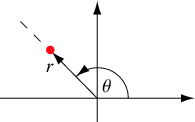
Lo mejor es dar la transformación inversa:\( x = r \cos \theta \),\( y = r \sin \theta \). Como todos sabemos por el cálculo, el jacobiano de la transformación es\( r \). De ahí que el siguiente resultado sea una consecuencia inmediata de nuestro teorema de cambio de variables:
Supongamos que\( (X, Y) \) tiene una distribución continua\( \R^2 \) con función de densidad de probabilidad\( f \), y que\( (R, \Theta) \) son las coordenadas polares de\( (X, Y) \). Entonces\( (R, \Theta) \) tiene la función de densidad de probabilidad\( g \) dada por\[ g(r, \theta) = f(r \cos \theta , r \sin \theta ) r, \quad (r, \theta) \in [0, \infty) \times [0, 2 \pi) \]
A continuación, para\( (x, y, z) \in \R^3 \), vamos a\( (r, \theta, z) \) denotar las coordenadas cilíndricas estándar, de manera que\( (r, \theta) \) son las coordenadas polares estándar de\( (x, y) \) como arriba, y la coordenada\( z \) se deja sin cambios. Dado nuestro resultado anterior, el de coordenadas cilíndricas no debería ser ninguna sorpresa.
Supongamos que\( (X, Y, Z) \) tiene una distribución continua\( \R^3 \) con función de densidad de probabilidad\( f \), y que\( (R, \Theta, Z) \) son las coordenadas cilíndricas de\( (X, Y, Z) \). Entonces\( (R, \Theta, Z) \) tiene la función de densidad de probabilidad\( g \) dada por\[ g(r, \theta, z) = f(r \cos \theta , r \sin \theta , z) r, \quad (r, \theta, z) \in [0, \infty) \times [0, 2 \pi) \times \R \]
Finalmente, para\( (x, y, z) \in \R^3 \), vamos a\( (r, \theta, \phi) \) denotar las coordenadas esféricas estándar correspondientes a las coordenadas cartesianas\((x, y, z)\), de manera que esa\( r \in [0, \infty) \) es la distancia radial,\( \theta \in [0, 2 \pi) \) es el ángulo azimutal, y\( \phi \in [0, \pi] \) es el ángulo polar. (A pesar de nuestro uso de la palabra estándar, diferentes notaciones y convenciones se utilizan en diferentes temas.)
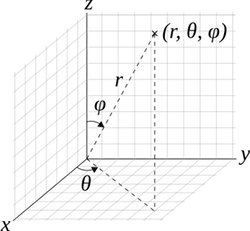
Una vez más, lo mejor es dar la transformación inversa:\( x = r \sin \phi \cos \theta \),\( y = r \sin \phi \sin \theta \),\( z = r \cos \phi \). Como recordamos del cálculo, el valor absoluto del jacobiano es\( r^2 \sin \phi \). De ahí que el siguiente resultado sea una consecuencia inmediata del cambio de teorema de variables (8):
Supongamos que\( (X, Y, Z) \) tiene una distribución continua\( \R^3 \) con función de densidad de probabilidad\( f \), y que\( (R, \Theta, \Phi) \) son las coordenadas esféricas de\( (X, Y, Z) \). Entonces\( (R, \Theta, \Phi) \) tiene la función de densidad de probabilidad\( g \) dada por\[ g(r, \theta, \phi) = f(r \sin \phi \cos \theta , r \sin \phi \sin \theta , r \cos \phi) r^2 \sin \phi, \quad (r, \theta, \phi) \in [0, \infty) \times [0, 2 \pi) \times [0, \pi] \]
Signo y Valor Absoluto
Nuestra siguiente discusión se refiere al signo y valor absoluto de una variable aleatoria de valor real.
Supongamos que\(X\) tiene una distribución continua\(\R\) con función de distribución\(F\) y función de densidad de probabilidad\(f\).
- \(\left|X\right|\)tiene función de distribución\(G\) dada por\(G(y) = F(y) - F(-y)\) for\(y \in [0, \infty)\).
- \(\left|X\right|\)tiene función de densidad de probabilidad\(g\) dada por\(g(y) = f(y) + f(-y)\) for\(y \in [0, \infty)\).
Prueba
- \( \P\left(\left|X\right| \le y\right) = \P(-y \le X \le y) = F(y) - F(-y) \)para\( y \in [0, \infty) \).
- Esto se desprende de la parte (a) tomando derivados con respecto a\( y \).
Recordemos que la función sign on\( \R \) (que no debe confundirse, por supuesto, con la función sinusoidal) se define de la siguiente manera:
\[ \sgn(x) = \begin{cases} -1, & x \lt 0 \\ 0, & x = 0 \\ 1, & x \gt 0 \end{cases} \]
Supongamos nuevamente que\( X \) tiene una distribución continua\( \R \) encendida con función de distribución\( F \) y función de densidad de probabilidad\( f \), y supongamos además que la distribución de\( X \) es simétrica alrededor de 0. Entonces
- \(\left|X\right|\)tiene función de distribución\(G\) dada por\(G(y) = 2 F(y) - 1\) for\(y \in [0, \infty)\).
- \(\left|X\right|\)tiene función de densidad de probabilidad\(g\) dada por\(g(y) = 2 f(y)\) for\(y \in [0, \infty)\).
- \(\sgn(X)\)se distribuye uniformemente en\(\{-1, 1\}\).
- \(\left|X\right|\)y\(\sgn(X)\) son independientes.
Prueba
- Esto se desprende del teorema anterior, ya que\( F(-y) = 1 - F(y) \) para\( y \gt 0 \) por simetría.
- Esto se desprende de la parte (a) tomando derivados.
- Tenga en cuenta eso\( \P\left[\sgn(X) = 1\right] = \P(X \gt 0) = \frac{1}{2} \) y así\( \P\left[\sgn(X) = -1\right] = \frac{1}{2} \) también.
- Si\( A \subseteq (0, \infty) \) entonces\[ \P\left[\left|X\right| \in A, \sgn(X) = 1\right] = \P(X \in A) = \int_A f(x) \, dx = \frac{1}{2} \int_A 2 \, f(x) \, dx = \P[\sgn(X) = 1] \P\left(\left|X\right| \in A\right) \]
Ejemplos y Aplicaciones
Esta subsección contiene ejercicios computacionales, muchos de los cuales involucran familias paramétricas especiales de distribuciones. Siempre es interesante cuando una variable aleatoria de una familia paramétrica puede transformarse en una variable de otra familia. También es interesante cuando una familia paramétrica es cerrada o invariante bajo alguna transformación en las variables de la familia. A menudo, tales propiedades son las que hacen que las familias paramétricas sean especiales en primer lugar. Tenga en cuenta estas propiedades cuando ocurran.
Dados
Recordemos que una matriz estándar es una matriz ordinaria de 6 caras, con caras etiquetadas de 1 a 6 (generalmente en forma de puntos). Un dado justo es aquel en el que las caras son igualmente probables. Un troquel plano ace-seis es un dado estándar en el que las caras 1 y 6 ocurren con probabilidad\(\frac{1}{4}\) cada una y las otras caras con probabilidad\(\frac{1}{8}\) cada una.
Supongamos que se tiran dos dados de seis caras y\((X_1, X_2)\) se registra la secuencia de puntuaciones. Encuentra la función de densidad de probabilidad de\(Y = X_1 + X_2\), la suma de las puntuaciones, en cada uno de los siguientes casos:
- Ambos dados son estándar y justos.
- Ambos dados son ace-seis planos.
- El primer dado es estándar y justo, y el segundo es ace-seis plano
- Los dados son los dos justos, pero el primer dado tiene caras etiquetadas con 1, 2, 2, 3, 3, 4 y el segundo dado tiene caras etiquetadas con 1, 3, 4, 5, 6, 8.
Contestar
Vamos a\(Y = X_1 + X_2\) denotar la suma de los puntajes.
-
\(y\) 2 3 4 5 6 7 8 9 10 11 12 \(\P(Y = y)\) \(\frac{1}{36}\) \(\frac{2}{36}\) \(\frac{3}{36}\) \(\frac{4}{36}\) \(\frac{5}{36}\) \(\frac{6}{36}\) \(\frac{5}{36}\) \(\frac{4}{36}\) \(\frac{3}{36}\) \(\frac{2}{36}\) \(\frac{1}{36}\) -
\(y\) 2 3 4 5 6 7 8 9 10 11 12 \(\P(Y = y)\) \(\frac{1}{16}\) \(\frac{1}{16}\) \(\frac{5}{64}\) \(\frac{3}{32}\) \(\frac{7}{64}\) \(\frac{3}{16}\) \(\frac{7}{64}\) \(\frac{3}{32}\) \(\frac{3}{32}\) \(\frac{1}{16}\) \(\frac{1}{16}\) -
\(y\) 2 3 4 5 6 7 8 9 10 11 12 \(\P(Y = y)\) \(\frac{2}{48}\) \(\frac{3}{48}\) \(\frac{4}{48}\) \(\frac{5}{48}\) \(\frac{6}{48}\) \(\frac{8}{48}\) \(\frac{6}{48}\) \(\frac{5}{48}\) \(\frac{4}{48}\) \(\frac{3}{48}\) \(\frac{2}{48}\) - La distribución es la misma que para dos dados estándar y justos en (a).
En el experimento de dados, seleccione dos dados y seleccione la variable aleatoria sum. Ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad para cada uno de los siguientes casos:
- dados justos
- dados planos ace-six
Supongamos que los dados\(n\) estándar, justos son rodados. Encuentre la función de densidad de probabilidad de las siguientes variables:
- la puntuación mínima
- la puntuación máxima.
Contestar
Dejar\(U\) denotar la puntuación mínima y\(V\) la puntuación máxima.
- \(f(u) = \left(1 - \frac{u-1}{6}\right)^n - \left(1 - \frac{u}{6}\right)^n, \quad u \in \{1, 2, 3, 4, 5, 6\}\)
- \(g(v) = \left(\frac{v}{6}\right)^n - \left(\frac{v - 1}{6}\right)^n, \quad v \in \{1, 2, 3, 4, 5, 6\}\)
En el experimento de dados, seleccione dados justos y seleccione cada una de las siguientes variables aleatorias. \(n\)Varía con la barra de desplazamiento y anote la forma de la función de densidad. Con\(n = 4\), ejecute la simulación 1000 veces y anote la concordancia entre la función de densidad empírica y la función de densidad de probabilidad.
- puntaje mínimo
- puntaje máximo.
Distribuciones Uniformes
Recordemos que para\( n \in \N_+ \), la medida estándar del tamaño de un conjunto\( A \subseteq \R^n \) es\[ \lambda_n(A) = \int_A 1 \, dx \] En particular,\( \lambda_1(A) \) es la longitud de\(A\) for\( A \subseteq \R \),\( \lambda_2(A) \) es el área de\(A\) for\( A \subseteq \R^2 \), y\( \lambda_3(A) \) es el volumen de\(A\) for\( A \subseteq \R^3 \). Consulte los detalles técnicos en (1) para obtener información más avanzada.
Ahora bien, si\( S \subseteq \R^n \) con\( 0 \lt \lambda_n(S) \lt \infty \), recordemos que la distribución uniforme on\( S \) es la distribución continua con función de densidad de probabilidad constante\(f\) definida por\( f(x) = 1 \big/ \lambda_n(S) \) for\( x \in S \). Las distribuciones uniformes se estudian con más detalle en el capítulo sobre Distribuciones Especiales.
Vamos\(Y = X^2\). Encuentre la función de densidad de probabilidad\(Y\) y dibuje el gráfico en cada uno de los siguientes casos:
- \(X\)se distribuye uniformemente en el intervalo\([0, 4]\).
- \(X\)se distribuye uniformemente en el intervalo\([-2, 2]\).
- \(X\)se distribuye uniformemente en el intervalo\([-1, 3]\).
Contestar
- \(g(y) = \frac{1}{8 \sqrt{y}}, \quad 0 \lt y \lt 16\)
- \(g(y) = \frac{1}{4 \sqrt{y}}, \quad 0 \lt y \lt 4\)
- \(g(y) = \begin{cases} \frac{1}{4 \sqrt{y}}, & 0 \lt y \lt 1 \\ \frac{1}{8 \sqrt{y}}, & 1 \lt y \lt 9 \end{cases}\)
Comparar las distribuciones en el último ejercicio. En la parte (c), señalar que incluso una simple transformación de una distribución simple puede producir una distribución complicada. En este caso particular, la complejidad es causada por el hecho de que\(x \mapsto x^2\) es uno a uno en parte del dominio\(\{0\} \cup (1, 3]\) y dos a uno en la otra parte\([-1, 1] \setminus \{0\}\).
Por otro lado, la distribución uniforme se conserva bajo una transformación lineal de la variable aleatoria.
Supongamos que\(\bs X\) tiene la distribución uniforme continua encendida\(S \subseteq \R^n\). Let\(\bs Y = \bs a + \bs B \bs X\), donde\(\bs a \in \R^n\) y\(\bs B\) es una\(n \times n\) matriz invertible. Entonces\(\bs Y\) se distribuye uniformemente en\(T = \{\bs a + \bs B \bs x: \bs x \in S\}\).
Prueba
Esto se desprende directamente del resultado general sobre las transformaciones lineales en (10). Tenga en cuenta que el PDF\( g \) de\( \bs Y \) es constante encendido\( T \).
Para los siguientes tres ejercicios, recordemos que la distribución uniforme estándar es la distribución uniforme en el intervalo\( [0, 1] \).
Supongamos que\(X\) y\(Y\) son independientes y que cada uno tiene la distribución uniforme estándar. Vamos\(U = X + Y\),\(V = X - Y\),\( W = X Y \),\( Z = Y / X \). Encuentra la función de densidad de probabilidad de cada uno de los siguientes:
- \((U, V)\)
- \(U\)
- \(V\)
- \( W \)
- \( Z \)
Contestar
- \(g(u, v) = \frac{1}{2}\)para\((u, v) \) en la región cuadrada\( T \subset \R^2 \) con vértices\(\{(0,0), (1,1), (2,0), (1,-1)\}\). Así\((U, V)\) se distribuye uniformemente en\( T \).
- \(g_1(u) = \begin{cases} u, & 0 \lt u \lt 1 \\ 2 - u, & 1 \lt u \lt 2 \end{cases}\)
- \(g_2(v) = \begin{cases} 1 - v, & 0 \lt v \lt 1 \\ 1 + v, & -1 \lt v \lt 0 \end{cases}\)
- \( h_1(w) = -\ln w \)para\( 0 \lt w \le 1 \)
- \( h_2(z) = \begin{cases} \frac{1}{2} & 0 \le z \le 1 \\ \frac{1}{2 z^2}, & 1 \le z \lt \infty \end{cases} \)
Supongamos que\(X\)\(Y\),, y\(Z\) son independientes, y que cada uno tiene la distribución uniforme estándar. Encuentra la función de densidad de probabilidad de\((U, V, W) = (X + Y, Y + Z, X + Z)\).
Contestar
\(g(u, v, w) = \frac{1}{2}\)para\((u, v, w)\) en la región rectangular\(T \subset \R^3\) con vértices\(\{(0,0,0), (1,0,1), (1,1,0), (0,1,1), (2,1,1), (1,1,2), (1,2,1), (2,2,2)\}\). Así\((U, V, W)\) se distribuye uniformemente en\(T\).
Supongamos que\((X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias independientes, cada una con la distribución uniforme estándar. Encuentre la función de distribución y la función de densidad de probabilidad de las siguientes variables.
- \(U = \min\{X_1, X_2 \ldots, X_n\}\)
- \(V = \max\{X_1, X_2, \ldots, X_n\}\)
Contestar
- \(G(t) = 1 - (1 - t)^n\)y\(g(t) = n(1 - t)^{n-1}\), tanto para\(t \in [0, 1]\)
- \(H(t) = t^n\)y\(h(t) = n t^{n-1}\), tanto para\(t \in [0, 1]\)
Ambas distribuciones en el último ejercicio son distribuciones beta. De manera más general, todas las estadísticas de orden de una muestra aleatoria de variables uniformes estándar tienen distribuciones beta, una de las razones de la importancia de esta familia de distribuciones. Las distribuciones beta se estudian con más detalle en el capítulo sobre Distribuciones especiales.
En el experimento estadístico de orden, seleccione la distribución uniforme.
- Set\(k = 1\) (esto da el mínimo\(U\)). Varíe\(n\) con la barra de desplazamiento y anote la forma de la función de densidad de probabilidad. Con\(n = 5\), ejecute la simulación 1000 veces y anote la concordancia entre la función de densidad empírica y la función de densidad de probabilidad verdadera.
- Varíe\(n\) con la barra de desplazamiento, establezca\(k = n\) cada vez (esto da el máximo\(V\)) y anote la forma de la función de densidad de probabilidad. Con\(n = 5\) ejecutar la simulación 1000 veces y comparar la función de densidad empírica y la función de densidad de probabilidad.
Dejar\(f\) denotar la función de densidad de probabilidad de la distribución uniforme estándar.
- Compute\(f^{*2}\)
- Compute\(f^{*3}\)
- Gráfica\( f \)\( f^{*2} \),, y\( f^{*3} \) en el mismo conjunto de ejes.
Contestar
- \(f^{*2}(z) = \begin{cases} z, & 0 \lt z \lt 1 \\ 2 - z, & 1 \lt z \lt 2 \end{cases}\)
- \(f^{*3}(z) = \begin{cases} \frac{1}{2} z^2, & 0 \lt z \lt 1 \\ 1 - \frac{1}{2}(z - 1)^2 - \frac{1}{2}(2 - z)^2, & 1 \lt z \lt 2 \\ \frac{1}{2} (3 - z)^2, & 2 \lt z \lt 3 \end{cases}\)
En el último ejercicio, se puede ver el comportamiento predicho por el teorema del límite central comenzando a emerger. Recordemos que si\((X_1, X_2, X_3)\) es una secuencia de variables aleatorias independientes, cada una con la distribución uniforme estándar, entonces\(f\)\(f^{*2}\),, y\(f^{*3}\) son las funciones de densidad de probabilidad de\(X_1\)\(X_1 + X_2\), y\(X_1 + X_2 + X_3\), respectivamente. De manera más general, si\((X_1, X_2, \ldots, X_n)\) es una secuencia de variables aleatorias independientes, cada una con la distribución uniforme estándar, entonces la distribución de\(\sum_{i=1}^n X_i\) (que tiene función de densidad de probabilidad\(f^{*n}\)) se conoce como la distribución Irwin-Hall con parámetro\(n\). Las distribuciones Irwin-Hall se estudian con más detalle en el capítulo sobre Distribuciones Especiales.
Abra el Simulador de Distribución Especial y seleccione la distribución Irwin-Hall. Varíe el parámetro\(n\) de 1 a 3 y anote la forma de la función de densidad de probabilidad. (Estas son las funciones de densidad en el ejercicio anterior). Para cada valor de\(n\), ejecute la simulación 1000 veces y compare la función de densidad empricial y la función de densidad de probabilidad.
Simulaciones
Un hecho notable es que la distribución uniforme estándar se puede transformar en casi cualquier otra distribución en\(\R\). Esto es particularmente importante para las simulaciones, ya que muchos lenguajes informáticos cuentan con un algoritmo para generar números aleatorios, que son simulaciones de variables independientes, cada una con la distribución uniforme estándar. Por el contrario, cualquier distribución continua soportada en un intervalo de\(\R\) puede transformarse en la distribución uniforme estándar.
Supongamos primero que\(F\) es una función de distribución para una distribución on\(\R\) (que puede ser discreta, continua o mixta), y dejar\(F^{-1}\) denotar la función quantile.
Supongamos que\(U\) tiene la distribución uniforme estándar. Entonces\(X = F^{-1}(U)\) tiene función de distribución\(F\).
Prueba
La propiedad crítica satisfecha por la función quantile (independientemente del tipo de distribución) es\( F^{-1}(p) \le x \) si y solo si\( p \le F(x) \) for\( p \in (0, 1) \) y\( x \in \R \). De ahí para\(x \in \R\),\(\P(X \le x) = \P\left[F^{-1}(U) \le x\right] = \P[U \le F(x)] = F(x)\).
Suponiendo que podemos calcular\(F^{-1}\), el ejercicio anterior muestra cómo podemos simular una distribución con función de distribución\(F\). Para replantear el resultado, podemos simular una variable con función\(F\) de distribución simplemente calculando un cuantil aleatorio. La mayoría de las aplicaciones de este proyecto utilizan este método de simulación. La primera imagen de abajo muestra la gráfica de la función de distribución de una distribución mixta bastante complicada, representada en azul sobre el eje horizontal. En la segunda imagen, observe cómo la distribución uniforme en\([0, 1]\), representada por la línea roja gruesa, se transforma, a través de la función cuantil, en la distribución dada.
.png)
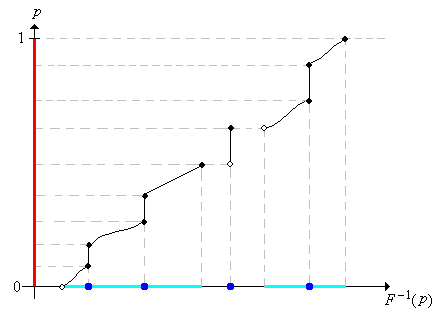
Hay una inversa parcial al resultado anterior, para distribuciones continuas.
Supongamos que\(X\) tiene una distribución continua en un intervalo\(S \subseteq \R\) Entonces\(U = F(X)\) tiene la distribución uniforme estándar.
Prueba
Para\( u \in (0, 1) \) recordar eso\( F^{-1}(u) \) es un cuantil de orden\( u \). Ya que\( X \) tiene una distribución continua,\[ \P(U \ge u) = \P[F(X) \ge u] = \P[X \ge F^{-1}(u)] = 1 - F[F^{-1}(u)] = 1 - u \] por lo tanto\( U \) se distribuye uniformemente en\( (0, 1) \).
Mostrar cómo simular la distribución uniforme en el intervalo\([a, b]\) con un número aleatorio. Usando su calculadora, simule 5 valores a partir de la distribución uniforme en el intervalo\([2, 10]\).
Contestar
\(X = a + U(b - a)\)donde\(U\) es un número aleatorio.
Distribuciones Beta
Supongamos que\(X\) tiene la función de densidad de probabilidad\(f\) dada por\(f(x) = 3 x^2\) for\(0 \le x \le 1\). Encuentre la función de densidad de probabilidad de cada uno de los siguientes:
- \(U = X^2\)
- \(V = \sqrt{X}\)
- \(W = \frac{1}{X}\)
Prueba
- \( g(u) = \frac{3}{2} u^{1/2} \), para\(0 \lt u \le 1\)
- \( h(v) = 6 v^5 \)para\( 0 \le v \le 1 \)
- \( k(w) = \frac{3}{w^4} \)para\( 1 \le w \lt \infty \)
Variables aleatorias\(X\)\(U\), y\(V\) en el ejercicio anterior tienen distribuciones beta, la misma familia de distribuciones que vimos en el ejercicio anterior para el mínimo y máximo de variables uniformes estándar independientes. En general, las distribuciones beta son ampliamente utilizadas para modelar proporciones y probabilidades aleatorias, así como cantidades físicas que toman valores en intervalos delimitados cerrados (que después de un cambio de unidades se puede tomar como ser\( [0, 1] \)). Por otro lado,\(W\) tiene una distribución de Pareto, llamada así por Vilfredo Pareto. La familia de distribuciones beta y la familia de distribuciones de Pareto se estudian con más detalle en el capítulo sobre Distribuciones especiales.
Supongamos que el radio\(R\) de una esfera tiene una función de densidad de probabilidad de distribución beta\(f\) dada por\(f(r) = 12 r^2 (1 - r)\) for\(0 \le r \le 1\). Encuentre la función de densidad de probabilidad de cada uno de los siguientes:
- La circunferencia\(C = 2 \pi R\)
- La superficie\(A = 4 \pi R^2\)
- El volumen\(V = \frac{4}{3} \pi R^3\)
Contestar
- \(g(c) = \frac{3}{4 \pi^4} c^2 (2 \pi - c)\)para\( 0 \le c \le 2 \pi\)
- \(h(a) = \frac{3}{8 \pi^2} \sqrt{a}\left(2 \sqrt{\pi} - \sqrt{a}\right)\)para\( 0 \le a \le 4 \pi\)
- \(k(v) = \frac{3}{\pi} \left[1 - \left(\frac{3}{4 \pi}\right)^{1/3} v^{1/3} \right]\)para\( 0 \le v \le \frac{4}{3} \pi\)
Supongamos que las calificaciones en una prueba son descritas por la variable aleatoria\( Y = 100 X \) donde\( X \) tiene la distribución beta con función de densidad de probabilidad\( f \) dada por\( f(x) = 12 x (1 - x)^2 \) for\( 0 \le x \le 1 \). Las calificaciones son generalmente bajas, por lo que el profesor decide curvar
las calificaciones usando la transformación\( Z = 10 \sqrt{Y} = 100 \sqrt{X}\). Encuentra la función de densidad de probabilidad de
- \( Y \)
- \( Z \)
Contestar
- \( g(y) = \frac{3}{25} \left(\frac{y}{100}\right)\left(1 - \frac{y}{100}\right)^2 \)para\( 0 \le y \le 100 \).
- \( h(z) = \frac{3}{1250} z \left(\frac{z^2}{10\,000}\right)\left(1 - \frac{z^2}{10\,000}\right)^2 \)para\( 0 \le z \le 100 \)
Juicios de Bernoulli
Recordemos que una secuencia de ensayos de Bernoulli es una secuencia\((X_1, X_2, \ldots)\) de variables aleatorias indicadoras independientes, distribuidas idénticamente. En la terminología habitual de la teoría de la confiabilidad,\(X_i = 0\) significa fracaso en juicio\(i\), mientras que\(X_i = 1\) significa éxito en el juicio\(i\). El parámetro básico del proceso es la probabilidad de éxito\(p = \P(X_i = 1)\), entonces\(p \in [0, 1]\). El proceso aleatorio lleva el nombre de Jacob Bernoulli y se estudia en detalle en el capítulo sobre los ensayos de Bernoulli.
Para\(i \in \N_+\), la función\(f\) de densidad de probabilidad de la variable de ensayo\(X_i\) es\(f(x) = p^x (1 - p)^{1 - x}\) para\(x \in \{0, 1\}\).
Prueba
Por definición,\( f(0) = 1 - p \) y\( f(1) = p \). Estos se pueden combinar de manera sucinta con la fórmula\( f(x) = p^x (1 - p)^{1 - x} \) para\( x \in \{0, 1\} \).
Ahora vamos a\(Y_n\) denotar el número de éxitos en los primeros\(n\) ensayos,\(Y_n = \sum_{i=1}^n X_i\) para que para\(n \in \N\).
\(Y_n\)tiene la función de densidad de probabilidad\(f_n\) dada por\[ f_n(y) = \binom{n}{y} p^y (1 - p)^{n - y}, \quad y \in \{0, 1, \ldots, n\}\]
Prueba
Ya hemos visto esta derivación antes. El número de cadenas de bits de longitud\( n \) con 1 ocurriendo exactamente\( y \) veces es\( \binom{n}{y} \) para\(y \in \{0, 1, \ldots, n\}\). Según los supuestos de los ensayos de Bernoulli, la probabilidad de cada cadena de bits es\( p^n (1 - p)^{n-y} \).
La distribución de\( Y_n \) es la distribución binomial con parámetros\(n\) y\(p\). La distribución binomial es estudiada con más detalle en el capítulo sobre los ensayos de Bernoulli
Para\( m, \, n \in \N \)
- \(f_n = f^{*n}\).
- \(f_m * f_n = f_{m + n}\).
Prueba
La parte (a) puede probarse directamente a partir de la definición de convolución, pero el resultado también se deriva simplemente del hecho de que\( Y_n = X_1 + X_2 + \cdots + X_n \).
De la parte (b) se deduce que si\(Y\) y\(Z\) son variables independientes, y que\(Y\) tiene la distribución binomial con parámetros\(n \in \N\) y\(p \in [0, 1]\) mientras\(Z\) tiene la distribución binomial con parámetro\(m \in \N\) y\(p\), entonces\(Y + Z\) tiene el binomio distribución con parámetro\(m + n\) y\(p\).
Encontrar la función de densidad de probabilidad de la diferencia entre el número de éxitos y el número de fracasos en ensayos de\(n \in \N\) Bernoulli con parámetro de éxito\(p \in [0, 1]\)
Contestar
\(f(k) = \binom{n}{(n+k)/2} p^{(n+k)/2} (1 - p)^{(n-k)/2}\)para\(k \in \{-n, 2 - n, \ldots, n - 2, n\}\)
La distribución de Poisson
Recordemos que la distribución de Poisson con parámetro\(t \in (0, \infty)\) tiene función de densidad de probabilidad\(f\) dada por\[ f_t(n) = e^{-t} \frac{t^n}{n!}, \quad n \in \N \] Esta distribución recibe el nombre de Simeon Poisson y es ampliamente utilizada para modelar el número de puntos aleatorios en una región de tiempo o espacio; el parámetro\(t\) es proporcional al tamaño de la regción. La distribución de Poisson se estudia en detalle en el capítulo sobre El proceso de Poisson.
Si\( a, \, b \in (0, \infty) \) entonces\(f_a * f_b = f_{a+b}\).
Prueba
Vamos\( z \in \N \). Usando la definición de convolución y el teorema binomial tenemos\ begin {align} (f_a * f_b) (z) & =\ sum_ {x = 0} ^z f_a (x) f_b (z - x) =\ sum_ {x = 0} ^z e^ {-a}\ frac {a^x} {x!} e^ {-b}\ frac {b^ {z - x}} {(z - x)!} = e^ {- (a + b)}\ frac {1} {z!} \ sum_ {x=0} ^z\ frac {z!} {x! (z - x)!} a^ {x} b^ {z - x}\\ & = e^ {- (a+b)}\ frac {1} {z!} \ sum_ {x=0} ^z\ binom {z} {x} a^x b^ {n-x} = e^ {- (a + b)}\ frac {(a + b) ^z} {z!} = f_ {a+b} (z)\ end {align}
El último resultado significa que si\(X\) y\(Y\) son variables independientes, y\(X\) tiene la distribución de Poisson con parámetro\(a \gt 0\) mientras que\(Y\) tiene la distribución de Poisson con parámetro\(b \gt 0\), entonces\(X + Y\) tiene la distribución de Poisson con parámetro\(a + b\). En términos del modelo de Poisson,\( X \) podría representar el número de puntos en una región\( A \) y\( Y \) el número de puntos en una región\( B \) (de los tamaños apropiados para que los parámetros sean\( a \) y\( b \) respectivamente). La independencia\( X \) y\( Y \) corresponde a las regiones\( A \) y\( B \) siendo disjuntas. Entonces\( X + Y \) es el número de puntos en\( A \cup B \).
La distribución exponencial
Recordemos que la distribución exponencial con parámetro de tasa\(r \in (0, \infty)\) tiene función de densidad de probabilidad\(f\) dada por\(f(t) = r e^{-r t}\) for\(t \in [0, \infty)\). Esta distribución se utiliza a menudo para modelar tiempos aleatorios como tiempos de falla y vida útil. En particular, los tiempos entre llegadas en el modelo de Poisson de puntos aleatorios en el tiempo tienen distribuciones exponenciales independientes, distribuidas idénticamente. La distribución exponencial se estudia con más detalle en el capítulo sobre Procesos de Poisson.
Mostrar cómo simular, con un número aleatorio, la distribución exponencial con parámetro de tasa\(r\). Usando tu calculadora, simula 5 valores a partir de la distribución exponencial con parámetro\(r = 3\).
Contestar
\(X = -\frac{1}{r} \ln(1 - U)\)donde\(U\) es un número aleatorio. Dado que también\(1 - U\) es un número aleatorio, una solución más sencilla es\(X = -\frac{1}{r} \ln U\).
Para el siguiente ejercicio, recuerde que las funciones de piso y techo\(\R\) están definidas por\[ \lfloor x \rfloor = \max\{n \in \Z: n \le x\}, \; \lceil x \rceil = \min\{n \in \Z: n \ge x\}, \quad x \in \R\]
Supongamos que\(T\) tiene la distribución exponencial con parámetro rate\(r \in (0, \infty)\). Encuentra la función de densidad de probabilidad de cada una de las siguientes variables aleatorias:
- \(Y = \lfloor T \rfloor\)
- \(Z = \lceil T \rceil\)
Contestar
- \(\P(Y = n) = e^{-r n} \left(1 - e^{-r}\right)\)para\(n \in \N\)
- \(\P(Z = n) = e^{-r(n-1)} \left(1 - e^{-r}\right)\)para\(n \in \N\)
Tenga en cuenta que las distribuciones en el ejercicio anterior son distribuciones geométricas sobre\(\N\) y sobre\(\N_+\), respectivamente. En muchos aspectos, la distribución geométrica es una versión discreta de la distribución exponencial.
Supongamos que\(T\) tiene la distribución exponencial con parámetro rate\(r \in (0, \infty)\). Encuentra la función de densidad de probabilidad de cada una de las siguientes variables aleatorias:
- \(X = T^2\)
- \(Y = e^{T}\)
- \(Z = \ln T\)
Contestar
- \(g(x) = r e^{-r \sqrt{x}} \big/ 2 \sqrt{x}\)para\(0 \lt x \lt \infty\)
- \(h(y) = r y^{-(r+1)} \)para\( 1 \lt y \lt \infty\)
- \(k(z) = r \exp\left(-r e^z\right) e^z\)para\(z \in \R\)
En el ejercicio anterior,\(Y\) tiene una distribución de Pareto mientras que\(Z\) tiene una distribución de valor extrema. Ambos se estudian con más detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\(X\) y\(Y\) son variables aleatorias independientes, teniendo cada una la distribución exponencial con el parámetro 1. Vamos\(Z = \frac{Y}{X}\).
- Encuentra la función de distribución de\(Z\).
- Encuentra la función de densidad de probabilidad de\(Z\).
Contestar
- \(G(z) = 1 - \frac{1}{1 + z}, \quad 0 \lt z \lt \infty\)
- \(g(z) = \frac{1}{(1 + z)^2}, \quad 0 \lt z \lt \infty\)
Supongamos que\(X\) tiene la distribución exponencial con parámetro rate\(a \gt 0\),\(Y\) tiene la distribución exponencial con parámetro rate\(b \gt 0\), y eso\(X\) y\(Y\) son independientes. Encuentra la función de densidad de probabilidad de\(Z = X + Y\) en cada uno de los siguientes casos.
- \(a = b\)
- \(a \ne b\)
Contestar
- \(h(z) = a^2 z e^{-a z}\)para\(0 \lt z \lt \infty\)
- \(h(z) = \frac{a b}{b - a} \left(e^{-a z} - e^{-b z}\right)\)para\(0 \lt z \lt \infty\)
Supongamos que\((T_1, T_2, \ldots, T_n)\) es una secuencia de variables aleatorias independientes, y que\(T_i\) tiene la distribución exponencial con parámetro rate\(r_i \gt 0\) para cada una\(i \in \{1, 2, \ldots, n\}\).
- Encuentra la función de densidad de probabilidad de\(U = \min\{T_1, T_2, \ldots, T_n\}\).
- Encuentra la función de distribución de\(V = \max\{T_1, T_2, \ldots, T_n\}\).
- Encuentra la función de densidad de probabilidad de\(V\) en el caso especial que\(r_i = r\) para cada uno\(i \in \{1, 2, \ldots, n\}\).
Contestar
- \(g(t) = a e^{-a t}\)para\(0 \le t \lt \infty\) donde\(a = r_1 + r_2 + \cdots + r_n\)
- \(H(t) = \left(1 - e^{-r_1 t}\right) \left(1 - e^{-r_2 t}\right) \cdots \left(1 - e^{-r_n t}\right)\)para\(0 \le t \lt \infty\)
- \(h(t) = n r e^{-r t} \left(1 - e^{-r t}\right)^{n-1}\)para\(0 \le t \lt \infty\)
Tenga en cuenta que el mínimo\(U\) en la parte (a) tiene la distribución exponencial con parámetro\(r_1 + r_2 + \cdots + r_n\). En particular, supongamos que un sistema en serie tiene componentes independientes, cada uno con una vida útil distribuida exponencialmente. Entonces la vida útil del sistema también se distribuye exponencialmente, y la tasa de fallas del sistema es la suma de las tasas de fallas de los componentes.
En el experimento estadístico de orden, seleccione la distribución exponencial.
- Set\(k = 1\) (esto da el mínimo\(U\)). Varíe\(n\) con la barra de desplazamiento y anote la forma de la función de densidad de probabilidad. Con\(n = 5\), ejecute la simulación 1000 veces y compare la función de densidad empírica y la función de densidad de probabilidad.
- Varíe\(n\) con la barra de desplazamiento y establezca\(k = n\) cada vez (esto da el máximo\(V\)). Observe la forma de la función de densidad. Con\(n = 5\), ejecute la simulación 1000 veces y compare la función de densidad empírica y la función de densidad de probabilidad.
Supongamos nuevamente que\((T_1, T_2, \ldots, T_n)\) es una secuencia de variables aleatorias independientes, y que\(T_i\) tiene la distribución exponencial con parámetro de tasa\(r_i \gt 0\) para cada una\(i \in \{1, 2, \ldots, n\}\). Entonces\[ \P\left(T_i \lt T_j \text{ for all } j \ne i\right) = \frac{r_i}{\sum_{j=1}^n r_j} \]
Prueba
Cuando\(n = 2\), el resultado se mostró en la sección sobre distribuciones conjuntas. Volviendo al caso de general\(n\), tenga en cuenta que\(T_i \lt T_j\) para todos\(j \ne i\) si y solo si\(T_i \lt \min\left\{T_j: j \ne i\right\}\). Obsérvese que el mínimo a la derecha es independiente\(T_i\) y por el resultado anterior, tiene una distribución exponencial con parámetro\(\sum_{j \ne i} r_j\).
El resultado en el ejercicio anterior es muy importante en la teoría de las cadenas de Markov en el tiempo continuo. Si tenemos un montón de despertadores independientes, con tiempos de alarma distribuidos exponencialmente, entonces la probabilidad de que el reloj\(i\) sea el primero en sonar es\(r_i \big/ \sum_{j = 1}^n r_j\).
La distribución Gamma
Recordemos que la distribución gamma (estándar) con parámetro shape\(n \in \N_+\) tiene función de densidad de probabilidad\[ g_n(t) = e^{-t} \frac{t^{n-1}}{(n - 1)!}, \quad 0 \le t \lt \infty \] Con un parámetro de forma entero positivo, como tenemos aquí, también se le conoce como la distribución Erlang, llamada así por Agner Erlang. Esta distribución es ampliamente utilizada para modelar tiempos aleatorios bajo ciertos supuestos básicos. En particular, los tiempos de llegada\( n \) th en el modelo de Poisson de puntos aleatorios en el tiempo tiene la distribución gamma con parámetro\( n \). La distribución de Erlang se estudia con más detalle en el capítulo sobre el Proceso de Poisson, y en mayor generalidad, la distribución gamma se estudia en el capítulo sobre Distribuciones Especiales.
Vamos\( g = g_1 \), y señalar que esta es la función de densidad de probabilidad de la distribución exponencial con el parámetro 1, que fue el tema de nuestra última discusión.
Si\( m, \, n \in \N_+ \) entonces
- \( g_n = g^{*n} \)
- \( g_m * g_n = g_{m+n} \)
Prueba
Parte (a) sostener trivialmente cuando\( n = 1 \). También, para\( t \in [0, \infty) \),\[ g_n * g(t) = \int_0^t g_n(s) g(t - s) \, ds = \int_0^t e^{-s} \frac{s^{n-1}}{(n - 1)!} e^{t-s} \, ds = e^{-t} \int_0^t \frac{s^{n-1}}{(n - 1)!} \, ds = e^{-t} \frac{t^n}{n!} = g_{n+1}(t) \] la Parte b) se desprende de (a).
Parte (b) significa que si\(X\) tiene la distribución gamma con el parámetro shape\(m\) y\(Y\) tiene la distribución gamma con el parámetro shape\(n\), y si\(X\) y\(Y\) son independientes, entonces\(X + Y\) tiene la distribución gamma con el parámetro shape\(m + n\). En el contexto del modelo de Poisson, la parte (a) significa que el\( n \) th tiempo de llegada es la suma de los tiempos interllegados\( n \) independientes, los cuales tienen una distribución exponencial común.
Supongamos que\(T\) tiene la distribución gamma con el parámetro shape\(n \in \N_+\). Encuentra la función de densidad de probabilidad de\(X = \ln T\).
Contestar
\(h(x) = \frac{1}{(n-1)!} \exp\left(-e^x\right) e^{n x}\)para\(x \in \R\)
La distribución de Pareto
Recordemos que la distribución de Pareto con parámetro de forma\(a \in (0, \infty)\) tiene función de densidad de probabilidad\(f\) dada por\[ f(x) = \frac{a}{x^{a+1}}, \quad 1 \le x \lt \infty\] Miembros de esta familia ya han surgido en varios de los ejercicios anteriores. La distribución de Pareto, llamada así por Vilfredo Pareto, es una distribución de cola pesada a menudo utilizada para modelar ingresos y otras variables financieras. La distribución de Pareto se estudia con más detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\(X\) tiene la distribución de Pareto con parámetro shape\(a\). Encuentra la función de densidad de probabilidad de cada una de las siguientes variables aleatorias:
- \(U = X^2\)
- \(V = \frac{1}{X}\)
- \(Y = \ln X\)
Contestar
- \(g(u) = \frac{a / 2}{u^{a / 2 + 1}}\)para\( 1 \le u \lt \infty\)
- \(h(v) = a v^{a-1}\)para\( 0 \lt v \lt 1\)
- \(k(y) = a e^{-a y}\)para\( 0 \le y \lt \infty\)
En el ejercicio anterior,\(V\) también tiene una distribución de Pareto pero con parámetro\(\frac{a}{2}\);\(Y\) tiene la distribución beta con parámetros\(a\) y\(b = 1\); y\(Z\) tiene la distribución exponencial con parámetro de tasa\(a\).
Mostrar cómo simular, con un número aleatorio, la distribución de Pareto con parámetro shape\(a\). Usando su calculadora, simule 5 valores de la distribución de Pareto con el parámetro shape\(a = 2\).
Contestar
Usando el método de cuantil aleatorio,\(X = \frac{1}{(1 - U)^{1/a}}\) donde\(U\) es un número aleatorio. Más simplemente,\(X = \frac{1}{U^{1/a}}\), ya que también\(1 - U\) es un número aleatorio.
La distribución normal
Recordemos que la distribución normal estándar tiene función de densidad de probabilidad\(\phi\) dada por\[ \phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} z^2}, \quad z \in \R\]
Supongamos que\(Z\) tiene la distribución normal estándar, y eso\(\mu \in (-\infty, \infty)\) y\(\sigma \in (0, \infty)\).
- Encuentra la función de densidad de probabilidad\( f \) de\(X = \mu + \sigma Z\)
- Esbozar la gráfica de\( f \), señalando las características cualitativas importantes.
Contestar
- \(f(x) = \frac{1}{\sqrt{2 \pi} \sigma} \exp\left[-\frac{1}{2} \left(\frac{x - \mu}{\sigma}\right)^2\right]\)para\( x \in \R\)
- \( f \)es simétrico sobre\( x = \mu \). \( f \)aumenta y luego disminuye, con modo\( x = \mu \). \( f \)es cóncava hacia arriba, luego hacia abajo, luego hacia arriba nuevamente, con puntos de inflexión en\( x = \mu \pm \sigma \). \( f(x) \to 0 \)como\( x \to \infty \) y como\( x \to -\infty \)
La variable aleatoria\(X\) tiene la distribución normal con parámetro de ubicación\(\mu\) y parámetro de escala\(\sigma\). La distribución normal es quizás la distribución más importante en probabilidad y estadística matemática, principalmente por el teorema del límite central, uno de los teoremas fundamentales. Es ampliamente utilizado para modelar medidas físicas de todo tipo que están sujetas a pequeños errores aleatorios. La distribución normal se estudia en detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\(Z\) tiene la distribución normal estándar. Encuentre la función de densidad de probabilidad\(Z^2\) y dibuje el gráfico.
Contestar
\(g(v) = \frac{1}{\sqrt{2 \pi v}} e^{-\frac{1}{2} v}\)para\( 0 \lt v \lt \infty\)
La variable aleatoria\(V\) tiene la distribución chi-cuadrada con 1 grado de libertad. Las distribuciones de chi-cuadrado se estudian en detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\( X \) y\( Y \) son variables aleatorias independientes, cada una con la distribución normal estándar, y dejan\( (R, \Theta) \) ser las coordenadas polares estándar\( (X, Y) \). Encuentra la función de densidad de probabilidad de
- \( (R, \Theta) \)
- \( R \)
- \( \Theta \)
Contestar
Tenga en cuenta que el PDF conjunto de\( (X, Y) \) es\[ f(x, y) = \phi(x) \phi(y) = \frac{1}{2 \pi} e^{-\frac{1}{2}\left(x^2 + y^2\right)}, \quad (x, y) \in \R^2 \] A partir del resultado por encima de las coordenadas polares, el PDF de\( (R, \Theta) \) es\[ g(r, \theta) = f(r \cos \theta , r \sin \theta) r = \frac{1}{2 \pi} r e^{-\frac{1}{2} r^2}, \quad (r, \theta) \in [0, \infty) \times [0, 2 \pi) \] A partir del teorema de factorización para PDFs conjuntos, se deduce que\( R \) tiene función de densidad de probabilidad\( h(r) = r e^{-\frac{1}{2} r^2} \) para\( 0 \le r \lt \infty \),\( \Theta \) es uniformemente distribuidos en\( [0, 2 \pi) \), y eso\( R \) y\( \Theta \) son independientes.
La distribución de\( R \) es la distribución (estándar) de Rayleigh, y lleva el nombre de John William Strutt, Lord Rayleigh. La distribución de Rayleigh se estudia con más detalle en el capítulo sobre Distribuciones Especiales.
La distribución normal estándar no tiene una función de cuantil de forma simple y cerrada, por lo que el método de simulación de cuantil aleatorio no funciona bien. Sin embargo, el último ejercicio señala el camino hacia un método alternativo de simulación.
Mostrar cómo simular un par de variables normales estándar independientes con un par de números aleatorios. Usando su calculadora, simule 6 valores de la distribución normal estándar.
Contestar
La distribución de Rayleigh en el último ejercicio tiene CDF\( H(r) = 1 - e^{-\frac{1}{2} r^2} \) para\( 0 \le r \lt \infty \), y por lo tanto función de cuantle\( H^{-1}(p) = \sqrt{-2 \ln(1 - p)} \) para\( 0 \le p \lt 1 \). Así podemos simular el radio polar\( R \) con un número aleatorio\( U \) por\( R = \sqrt{-2 \ln(1 - U)} \), o un poco más simplemente por\(R = \sqrt{-2 \ln U}\), ya que también\(1 - U\) es un número aleatorio. Podemos simular el ángulo polar\( \Theta \) con un número aleatorio\( V \) por\( \Theta = 2 \pi V \). Entonces, un par de variables normales estándar independientes pueden ser simuladas por\( X = R \cos \Theta \),\( Y = R \sin \Theta \).
La distribución de Cauchy
Supongamos que\(X\) y\(Y\) son variables aleatorias independientes, cada una con la distribución normal estándar. Encuentra la función de densidad de probabilidad de\(T = X / Y\).
Contestar
Como de costumbre, vamos a\( \phi \) denotar el PDF normal estándar,\( \phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-z^2/2}\) para que para\( z \in \R \). Usando el teorema sobre el cociente anterior, el PDF\( f \) de\( T \) se da por\[f(t) = \int_{-\infty}^\infty \phi(x) \phi(t x) |x| dx = \frac{1}{2 \pi} \int_{-\infty}^\infty e^{-(1 + t^2) x^2/2} |x| dx, \quad t \in \R\] Usando simetría y una simple sustitución,\[ f(t) = \frac{1}{\pi} \int_0^\infty x e^{-(1 + t^2) x^2/2} dx = \frac{1}{\pi (1 + t^2)}, \quad t \in \R \]
La variable aleatoria\(T\) tiene la distribución (estándar) de Cauchy, llamada así por Augustin Cauchy. La distribución de Cauchy se estudia en detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que una fuente de luz está a 1 unidad de distancia de la posición 0 en una pared recta infinita. Hacemos brillar la luz en la pared un ángulo\( \Theta \) con respecto a la perpendicular, donde\( \Theta \) se distribuye uniformemente sobre\( \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) \). Encuentra la función de densidad de probabilidad de la posición del haz de luz\( X = \tan \Theta \) en la pared.
Contestar
El PDF de\( \Theta \) es\( f(\theta) = \frac{1}{\pi} \) para\( -\frac{\pi}{2} \le \theta \le \frac{\pi}{2} \). La transformación es\( x = \tan \theta \) así la transformación inversa es\( \theta = \arctan x \). Recordemos que\( \frac{d\theta}{dx} = \frac{1}{1 + x^2} \), así por el cambio de variables fórmula,\( X \) tiene PDF\(g\) dado por\[ g(x) = \frac{1}{\pi \left(1 + x^2\right)}, \quad x \in \R \]
Así,\( X \) también tiene la distribución estándar de Cauchy. Claramente podemos simular un valor de la distribución de Cauchy por\( X = \tan\left(-\frac{\pi}{2} + \pi U\right) \) donde\( U \) es un número aleatorio. Este es el método del cuantil aleatorio.
Abrir el experimento de Cauchy, que es una simulación del problema de la luz en el ejercicio anterior. Mantenga los valores de los parámetros predeterminados y ejecute el experimento en modo de un solo paso varias veces. Luego ejecute el experimento 1000 veces y compare la función de densidad empírica y la función de densidad de probabilidad.


