5.40: La distribución Zeta
- Page ID
- 151669
La distribución zeta se utiliza para modelar el tamaño o rangos de ciertos tipos de objetos elegidos aleatoriamente de ciertos tipos de poblaciones. Los ejemplos típicos incluyen la frecuencia de ocurrencia de una palabra elegida aleatoriamente de un texto, o el rango poblacional de una ciudad elegida aleatoriamente de un país. La distribución zeta también es conocida como la distribución Zipf, en honor al lingüista estadounidense George Zipf.
Teoría Básica
La función Zeta
La función zeta de Riemann\(\zeta\), que lleva el nombre de Bernhard Riemann, se define de la siguiente manera:\[ \zeta(a) = \sum_{n=1}^\infty \frac{1}{n^a}, \quad a \in (1, \infty) \]
Tal vez recuerde del cálculo que la serie en la función zeta converge para\(a \gt 1\) y diverge para\(a \le 1\).
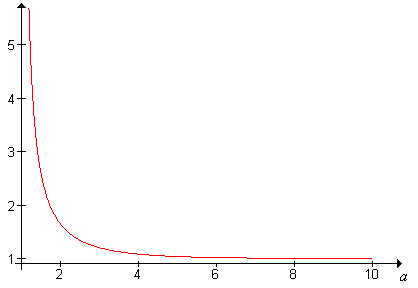
La función zeta satisface las siguientes propiedades:
- \(\zeta\)es decreciente.
- \(\zeta\)es cóncavo hacia arriba.
- \(\zeta(a) \downarrow 1\)como\(a \uparrow \infty\)
- \(\zeta(a) \uparrow \infty\)como\(a \downarrow 1\)
La función zeta es trascendental, y la mayoría de sus valores deben ser aproximados. Sin embargo, se\(\zeta(a)\) puede dar explícitamente para valores enteros pares de\(a\); en particular,\(\zeta(2) = \frac{\pi^2}{6}\) y\(\zeta(4) = \frac{\pi^4}{90}\).
La función de densidad de probabilidad
La distribución zeta con parámetro shape\( a \in (1, \infty) \) es una distribución discreta\( \N_+ \) con función de densidad de probabilidad\( f \) dada por. \[ f(n) = \frac{1}{\zeta(a) n^a}, \quad n \in \N_+ \]
- \( f \)está disminuyendo con el modo\( n = 1 \).
- Cuando se alisa,\( f \) es cóncava hacia arriba.
Prueba
Claramente\( f \) es un PDF válido, ya que por definición,\( \zeta(a) \) es la constante normalizadora para la función\( n \mapsto \frac{1}{n^a} \) on\( \N_+ \). La parte (a) es clara. Para la parte (b), tenga en cuenta que la función\( x \mapsto x^{-a} \) on\( [1, \infty) \) tiene una segunda derivada positiva.
Abra el simulador de distribución especial y seleccione la distribución zeta. Variar el parámetro shape y anotar la forma de la función de densidad de probabilidad. Para los valores seleccionados del parámetro, ejecute la simulación 1000 veces y compare la función de densidad empírica con la función de densidad de probabilidad.
La función de distribución y la función cuantil no tienen formas simples cerradas, excepto en términos de otras funciones especiales.
Abra la calculadora de distribución especial y seleccione la distribución zeta. Varíe el parámetro y anote la forma de las funciones de distribución y densidad de probabilidad. Para los valores seleccionados del parámetro, compute la mediana y el primer y tercer cuartiles.
Momentos
Supongamos que\( N \) tiene la distribución zeta con parámetro shape\( a \in (1, \infty) \). Los momentos de se\( X \) pueden expresar fácilmente en términos de la función zeta.
Si\( k \ge a - 1 \),\( \E(X) = \infty \). Si\( k \lt a - 1 \),\[\E\left(N^k\right) = \frac{\zeta(a - k)}{\zeta(a)}\]
Prueba
Tenga en cuenta que\[ \E\left(N^k\right) = \sum_{n=1}^\infty n^k \frac{1}{\zeta(a) n^a} = \frac{1}{\zeta(a)} \sum_{n=1}^\infty \frac{1}{n^{a - k}}\] Si\( a - k \le 1 \), la última suma diverge a\( \infty \). Si\( a - k \gt 1 \), la suma converge a\( \zeta(a - k) \)
La media y varianza de\(N\) son las siguientes:
- Si\( a \gt 2 \),\[\E(N) = \frac{\zeta(a - 1)}{\zeta(a)}\]
- Si\( a \gt 3 \),\[\var(N) = \frac{\zeta(a - 2)}{\zeta(a)} - \left(\frac{\zeta(a - 1)}{\zeta(a)}\right)^2\]
Abra el simulador de distribución especial y seleccione la distribución zeta. Varíe el parámetro y anote la forma y ubicación de la barra de desviación\( \pm \) estándar media. Para los valores seleccionados del parámetro, ejecute la simulación 1000 veces y compare la media empírica y la desviación estándar con la media de distribución y la desviación estándar.
La asimetría y curtosis de\(N\) son las siguientes:
- Si\( a \gt 4 \),\[ \skw(N) = \frac{\zeta(a - 3) \zeta^2(a) - 3 \zeta(a - 1) \zeta(a - 2) \zeta(a) + 2 \zeta^3(a - 1)}{[\zeta(a - 2) \zeta(a) - \zeta^2(a - 1)]^{3/2}} \]
- Si\( a \gt 5 \),\[ \kur(N) = \frac{\zeta(a - 4) \zeta^3(a) - 4 \zeta(a - 1) \zeta(a - 3) \zeta^2(a) + 6 \zeta^2(a - 1) \zeta(a - 2) \zeta(a) - 3 \zeta^4(a - 1)}{\left[\zeta(a - 2) \zeta(a) - \zeta^2(a - 1)\right]^2} \]
Prueba
Estos resultados se derivan del resultado del momento general anterior y las fórmulas computacionales estándar para asimetría y curtosis.
La función generadora de probabilidad de se\( N \) puede expresar en términos de la función polilogaritmo\( \Li \) que se introdujo en la sección sobre la distribución exponencial-logarítmica. Recordemos que el polilogaritmo de orden\( s \in \R \) está definido por\[ \Li_s(x) = \sum_{k=1}^\infty \frac{x^k}{k^s}, \quad x \in (-1, 1) \]
\( N \)tiene la función de generación de probabilidad\( P \) dada por\[ P(t) = \E\left(t^N\right) = \frac{\Li_a(t)}{\zeta(a)}, \quad t \in (-1, 1) \]
Prueba
Tenga en cuenta que\[ \E\left(t^N\right) = \sum_{n=1}^\infty t^n \frac{1}{n^a \zeta(a)} = \frac{1}{\zeta(a)} \sum_{n=1}^\infty \frac{t^n}{n^a} \] La última suma es\( \Li_a(t) \).
Distribuciones Relacionadas
En un sentido algebraico, la distribución zeta es una versión discreta de la distribución de Pareto. Recordemos que si\( a \gt 1 \), la distribución de Pareto con parámetro shape\( a - 1 \) es una distribución continua\( [1, \infty) \) con función de densidad de probabilidad\[ f(x) = \frac{a - 1}{x^a}, \quad x \in [1, \infty) \]
Naturalmente, los límites de la distribución zeta con respecto al parámetro shape\( a \) son de interés.
La distribución zeta con parámetro shape\( a \in (1, \infty) \) converge a masa puntual en 1 as\( a \to \infty \).
Prueba
Para el PDF\( f \) anterior, tenga en cuenta que\( f(1) = \zeta(a) \to 1 \) como\( a \to \infty \) y para\( n \in \{2, 3, \ldots\} \),\( f(n) = 1 \big/ n^a \zeta(a) \to 0 \) como\( a \to \infty \)
Finalmente, la distribución zeta es un miembro de la familia de distribuciones exponenciales generales.
Supongamos que\(N\) tiene la distribución zeta con parámetro\(a\). Entonces la distribución es una familia exponencial de un parámetro con parámetro natural\(a\) y estadística natural\(-\ln N\).
Prueba
Esto se desprende de la definición de la distribución exponencial general, ya que el PDF zeta se puede escribir en la forma\[ f(n) = \frac{1}{\zeta(a)} \exp(-a \ln n), \quad n \in \N_+ \]
Ejercicios Computacionales
Vamos a\(N\) denotar la frecuencia de ocurrencia de una palabra elegida al azar a partir de un cierto texto, y supongamos que\(X\) tiene la distribución zeta con parámetro\(a = 2\). Encuentra\(\P(N \gt 4)\).
Contestar
\(\P(N \gt 4) = 1 - \frac{49}{6 \pi^2} \approx 0.1725\)
Supongamos que\(N\) tiene la distribución zeta con parámetro\(a = 6\). Aproximar cada uno de los siguientes:
- \(\E(N)\)
- \(\var(N)\)
- \( \skw(N) \)
- \( \kur(N) \)
Contestar
- \(\E(N) \approx 1.109\)
- \(\var(N) \approx 0.025\)
- \( \skw(N) \approx 11.700 \)
- \( \kur(N) \approx 309.19 \)


