8.2: Estimación del modelo normal

Última actualización
Guardar como PDF

Page ID: 151951

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\R}{\mathbb{R}}$$\newcommand{\N}{\mathbb{N}}$$\newcommand{\Z}{\mathbb{Z}}$$\newcommand{\P}{\mathbb{P}}$$\newcommand{\E}{\mathbb{E}}$$\newcommand{\var}{\text{var}}$$\newcommand{\sd}{\text{sd}}$$\newcommand{\bs}{\boldsymbol}$

Teoría Básica

El modelo normal

La distribución normal es quizás la distribución más importante en el estudio de la estadística matemática, en parte por el teorema del límite central. Como consecuencia de este teorema, una cantidad medida que está sujeta a numerosos errores pequeños y aleatorios tendrá, al menos aproximadamente, una distribución normal. Tales variables son ubicuas en experimentos estadísticos, en sujetos que varían desde las ciencias físicas y biológicas hasta las ciencias sociales.

Entonces en esta sección, asumimos que$\bs{X} = (X_1, X_2, \ldots, X_n)$ es una muestra aleatoria de la distribución normal con media$\mu$ y desviación estándar$\sigma$. Nuestro objetivo es construir intervalos de confianza para$\mu$ e$\sigma$ individualmente, y luego más generalmente, conjuntos de confianza para$ (\mu, \sigma) $. Estos se encuentran entre los casos especiales más importantes de estimación de conjuntos. Una sección paralela sobre Pruebas en el Modelo Normal se encuentra en el capítulo sobre Pruebas de Hipótesis. Primero necesitamos revisar algunos hechos básicos que serán críticos para nuestro análisis.

Recordemos que la media muestral$ M $ y la varianza muestral$ S^2 $ son\[ M = \frac{1}{n} \sum_{i=1}^n X_i, \quad S^2 = \frac{1}{n - 1} \sum_{i=1}^n (X_i - M)^2\]

De nuestro estudio de estimación puntual, recordemos que$ M $ es un estimador imparcial y consistente de$ \mu $ while$ S^2 $ es un estimador imparcial y consistente de$ \sigma^2 $. A partir de estas estadísticas básicas podemos construir las variables pivotes que serán utilizadas para construir nuestras estimaciones de intervalos. Los siguientes resultados se establecieron en el apartado de Propiedades Especiales de la Distribución Normal.

Definir\[ Z = \frac{M - \mu}{\sigma \big/ \sqrt{n}}, \quad T = \frac{M - \mu}{S \big/ \sqrt{n}}, \quad V = \frac{n - 1}{\sigma^2} S^2 \]

$ Z $tiene la distribución normal estándar.
$ T $tiene la$ t $ distribución estudiantil con$ n - 1 $ grados de libertad.
$ V $tiene la distribución chi-cuadrada con$ n - 1 $ grados de libertad.
$ Z $y$ V $ son independientes.

De ello se deduce que cada una de estas variables aleatorias es una variable pivote para$ (\mu, \sigma) $ ya que las distribuciones no dependen de los parámetros, sino que las propias variables dependen funcionalmente de uno o ambos parámetros. Las variables de pivote$ Z $ y se$ T $ utilizarán para construir estimaciones de intervalo de$ \mu $ while se$ V $ utilizarán para construir estimaciones de intervalo de$ \sigma^2 $. Para construir nuestras estimaciones, necesitaremos cuantiles de estas distribuciones estándar. Los cuantiles se pueden calcular utilizando la calculadora de distribución especial o a partir de la mayoría de los paquetes de software matemáticos y estadísticos. Aquí está la notación que usaremos:

Dejar$ p \in (0, 1) $ y$ k \in \N_+ $.

$ z(p) $denota el cuantil de orden$ p $ para la distribución normal estándar.
$t_k(p)$denota el cuantil de orden$ p $ para la$ t $ distribución estudiantil con$ k $ grados de libertad.
$ \chi^2_k(p) $denota el cuantil de orden$ p $ para la distribución de chi-cuadrado con$ k $ grados de libertad

Dado que las$ t $ distribuciones estándar normales y estudiantiles son simétricas alrededor de 0, se deduce que$ z(1 - p) = -z(p) $ y$ t_k(1 - p) = -t_k(p) $ para$ p \in (0, 1) $ y$ k \in \N_+ $. Por otro lado, la distribución chi-cuadrada no es simétrica.

Intervalos de confianza para$ \mu $$ \sigma $ con

Para nuestra primera discusión, asumimos que la media de distribución$ \mu $ es desconocida pero$ \sigma $ se conoce la desviación estándar. Esto no siempre es una suposición artificial. A menudo hay situaciones en las que$ \sigma $ es estable a lo largo del tiempo, y por lo tanto se conoce al menos aproximadamente, mientras que$ \mu $ los cambios se deben a diferentes tratamientos. Se dan ejemplos en los ejercicios computacionales a continuación. La variable pivote$ Z $ conduce a intervalos de confianza para$ \mu $.

Para$ \alpha \in (0, 1) $,

$ \left[M - z\left(1 - \frac{\alpha}{2}\right) \frac{\sigma}{\sqrt{n}}, M + z\left(1 - \frac{\alpha}{2}\right) \frac{\sigma}{\sqrt{n}}\right] $es un intervalo de$ 1 - \alpha $ confianza para$ \mu $.
$ M - z(1 - \alpha) \frac{\sigma}{\sqrt{n}} $es un límite inferior de$ 1 - \alpha $ confianza para$ \mu $
$ M + z(1 - \alpha) \frac{\sigma}{\sqrt{n}} $es un límite superior de$ 1 - \alpha $ confianza para$ \mu $

Prueba

Dado que$ Z = \frac{M - \mu}{\sigma / \sqrt{n}} $ tiene la distribución normal estándar, cada uno de los siguientes eventos tiene probabilidad$ 1 - \alpha $ por definición de los cuantiles:

$ \left\{-z\left(1 - \frac{\alpha}{2}\right) \le \frac{M - \mu}{\sigma / \sqrt{n}} \le z\left(1 - \frac{\alpha}{2}\right)\right\} $
$ \left\{\frac{M - \mu}{\sigma / \sqrt{n}} \ge z(1 - \alpha)\right\} $
$ \left\{\frac{M - \mu}{\sigma / \sqrt{n}} \le -z(1 - \alpha)\right\} $

En cada caso, resolver la desigualdad para$ \mu $ da el resultado.

Estas son las estimaciones de intervalos estándar para$ \mu $ cuando$ \sigma $ se conoce. El intervalo de confianza de dos lados en (a) es simétrico con respecto a la media de la muestra$ M $, y como muestra la prueba, corresponde a igual probabilidad$ \frac{\alpha}{2} $ en cada cola de la distribución de la variable pivote$ Z $. Pero claro, este no es el único intervalo de$ 1 - \alpha $ confianza de dos lados; podemos dividir la probabilidad de$ \alpha $ todos modos que queramos entre las colas izquierda y derecha de la distribución de$ Z $.

Para cada$\alpha, \, p \in (0, 1)$, un intervalo de$1 - \alpha$ confianza para$\mu$\[ \left[M - z(1 - p \alpha) \frac{\sigma}{\sqrt{n}}, M - z(\alpha - p \alpha) \frac{\sigma}{\sqrt{n}} \right] \]

$ p = \frac{1}{2} $da el intervalo de confianza simétrico, igual a la cola.
$ p \to 0 $da el intervalo con el límite superior de confianza.
$ p \to 1 $da el intervalo con el límite inferior de confianza.

Prueba

A partir de la distribución normal de$ M $ y la definición de la función cuantil,\[ \P \left[ z(\alpha - p \, \alpha) \lt \frac{M - \mu}{\sigma / \sqrt{n}} \lt z(1 - p \alpha) \right] = 1 - \alpha \] El resultado sigue entonces resolviendo para$\mu$ en la desigualdad.

En cuanto a la distribución de la variable pivote$ Z $, como muestra la prueba, el intervalo de confianza de dos lados anterior corresponde a$ p \alpha $ en la cola derecha y$ (1 - p) \alpha $ en la cola izquierda. A continuación, estudiemos la duración de este intervalo de confianza.

Para$ \alpha, \, p \in (0, 1) $, la longitud (determinista) del intervalo de$ 1 - \alpha $ confianza de dos lados anterior es\[L = \frac{\left[z(1 - p \alpha) - z(\alpha - p \alpha)\right] \sigma}{\sqrt{n}} \]

$L$es una función decreciente de$\alpha$, y$L \downarrow 0$ como$\alpha \uparrow 1$ y$L \uparrow \infty$ como$\alpha \downarrow 0$.
$L$es una función decreciente de$n$, y$L \downarrow 0$ como$n \uparrow \infty$.
$L$es una función creciente de$\sigma$, y$L \downarrow 0$ como$\sigma \downarrow 0$ y$L \uparrow \infty$ como$\sigma \uparrow \infty$.
En función de$ p $,$L$ disminuye y luego aumenta, con mínimo en el punto de simetría$p = \frac{1}{2}$.

El último resultado muestra nuevamente que existe una compensación entre el nivel de confianza y la duración del intervalo de confianza. Si$n$ y$p$ son fijos, podemos disminuir$L$, y de ahí apretar nuestra estimación, sólo a costa de disminuir nuestra confianza en la estimación. Por el contrario, podemos aumentar nuestra confianza en la estimación sólo a expensas de aumentar la longitud del intervalo. En términos de$p$, el mejor de los intervalos de$1 - \alpha$ confianza de dos lados (y el que casi siempre se usa) es simétrico, intervalo de cola igual con$ p = \frac{1}{2} $:

Utilice el experimento de estimación de medias para explorar el procedimiento. Seleccione la distribución normal y seleccione pivote normal. Utilice varios valores de parámetros, niveles de confianza, tamaños de muestra y tipos de intervalos. Para cada configuración, ejecute el experimento 1000 veces. A medida que se ejecuta la simulación, tenga en cuenta que el intervalo de confianza captura con éxito la media si y solo si el valor de la variable pivote está entre los cuantiles. Anote el tamaño y ubicación de los intervalos de confianza y compare la proporción de intervalos exitosos con el nivel de confianza teórico.

Para los intervalos de confianza estándar, vamos a$d$ denotar la distancia entre la media de la muestra$M$ y un punto final. Es decir,\[ d = z_\alpha \frac{\sigma}{\sqrt{n}} \] donde$z_\alpha = z(1 - \alpha /2 )$ para el intervalo de dos lados y$z_\alpha = z(1 - \alpha)$ para el intervalo de confianza superior o inferior. El número$ d $ es el margen de error de la estimación.

Tenga en cuenta que$d$ es determinista, y la longitud del intervalo estándar de dos lados es$L = 2 d$. En muchos casos, el primer paso en el diseño del experimento es determinar el tamaño de muestra necesario para estimar$\mu$ con un margen de error dado y un nivel de confianza dado.

El tamaño muestral necesario para estimar$\mu$ con confianza$1 - \alpha$ y margen de error$d$ es\[ n = \left \lceil \frac{z_\alpha^2 \sigma^2}{d^2} \right\rceil \]

Prueba

Esto sigue resolviendo for$ n $ en la definición$ d $ anterior, y luego redondeando hasta el siguiente entero.

Tenga en cuenta que$n$ varía directamente con$z_\alpha^2$ y con$\sigma^2$ e inversamente con$d^2$. Este último hecho implica una ley de rentabilidad decreciente en la reducción del margen de error. Por ejemplo, si queremos reducir un determinado margen de error por un factor de$\frac{1}{2}$, debemos aumentar el tamaño de la muestra en un factor de 4.

Intervalos de confianza para$ \mu $ con$ \sigma $ desconocido

Para nuestra siguiente discusión, asumimos que la media de distribución$ \mu $ y la desviación estándar$ \sigma $ son desconocidas, la situación habitual. En este caso, podemos usar la variable$ T $ pivote, en lugar de la variable$ Z $ pivote, para construir intervalos de confianza para$ \mu $.

Para$ \alpha \in (0, 1) $,

$ \left[M - t_{n-1}\left(1 - \frac{\alpha}{2}\right) \frac{S}{\sqrt{n}}, M + t_{n-1}\left(1 - \frac{\alpha}{2}\right) \frac{S}{\sqrt{n}}\right] $es un intervalo de$ 1 - \alpha $ confianza para$ \mu $.
$ M - t_{n-1}(1 - \alpha) \frac{S}{\sqrt{n}} $es un límite$ 1 - \alpha $ inferior para$ \mu $
$ M + t_{n-1}(1 - \alpha) \frac{S}{\sqrt{n}} $es un límite$ 1 - \alpha $ superior para$ \mu $

Prueba

Ya que$ T = \frac{M - \mu}{S / \sqrt{n}} $ tiene la$ t $ distribución con$ n - 1 $ grados de libertad, cada uno de los siguientes eventos tiene probabilidad$ 1 - \alpha $, por definición de los cuantiles:

$ \left\{-t_{n-1}\left(1 - \frac{\alpha}{2}\right) \le \frac{M - \mu}{S / \sqrt{n}} \le t_{n-1}\left(1 - \frac{\alpha}{2}\right)\right\} $
$ \left\{\frac{M - \mu}{S / \sqrt{n}} \ge t_{n-1}(1 - \alpha)\right\} $
$ \left\{\frac{M - \mu}{S / \sqrt{n}} \le -t_{n-1}(1 - \alpha)\right\} $

En cada caso, resolver por$ \mu $ en la desigualdad da el resultado.

Estas son las estimaciones de intervalo estándar de$ \mu $ con$ \sigma $ desconocido. El intervalo de confianza de dos lados en (a) es simétrico con respecto a la media de la muestra$ M $ y corresponde a igual probabilidad$ \frac{\alpha}{2} $ en cada cola de la distribución de la variable pivote$ T $. Como antes, este no es el único intervalo de confianza; podemos dividir$ \alpha $ entre las colas izquierda y derecha de la manera que queramos.

Para cada$\alpha, \, p \in (0, 1)$, un intervalo de$1 - \alpha$ confianza para$\mu$\[ \left[M - t_{n-1}(1 - p \alpha) \frac{S}{\sqrt{n}}, M - t_{n-1}(\alpha - p \alpha) \frac{S}{\sqrt{n}} \right] \]

$ p = \frac{1}{2} $da el intervalo de confianza simétrico, igual a la cola.
$ p \to 0 $da el intervalo con el límite superior de confianza.
$ p \to 1 $da el intervalo con el límite inferior de confianza.

Prueba

Ya que$ T $ tiene la$ t $ distribución estudiantil con$ n - 1 $ grados de libertad, se desprende de la definición de los cuantiles que\[ \P \left[ t_{n-1}(\alpha - p \alpha) \lt \frac{M - \mu}{S \big/ \sqrt{n}} \lt t_{n-1}(1 - p \alpha) \right] = 1 - \alpha \] El resultado luego sigue resolviendo para$\mu$ en la desigualdad.

El intervalo de confianza de dos lados anterior corresponde a$ p \alpha $ en la cola derecha y$ (1 - p) \alpha $ en la cola izquierda de la distribución de la variable pivote$ T $. A continuación, estudiemos la duración de esta interal de confianza.

Para$ \alpha, \, p \in (0, 1) $, la longitud (aleatoria) del intervalo de$ 1 - \alpha $ confianza de dos lados anterior es\[ L = \frac{t_{n-1}(1 - p \alpha) - t_{n-1}(\alpha - p \alpha)} {\sqrt{n}} S \]

$L$es una función decreciente de$\alpha$, y$L \downarrow 0$ como$\alpha \uparrow 1$ y$L \uparrow \infty$ como$\alpha \downarrow 0$.
En función de$ p $,$L$ disminuye y luego aumenta, con mínimo en el punto de simetría$p = \frac{1}{2}$.
\[ \E(L) = \frac{[t_{n-1}(1 - p \alpha) - t_{n-1}(\alpha - p \alpha)] \sqrt{2} \sigma \Gamma(n/2)}{\sqrt{n (n - 1)} \Gamma[(n - 1)/2]} \]
\[ \var(L) = \frac{1}{n}\left[t_{n-1}(1 - p \alpha) - t_{n-1}(\alpha - p \alpha)\right]^2 \sigma^2\left[1 - \frac{2 \Gamma^2(n / 2)}{(n - 1) \Gamma^2[(n - 1) / 2]}\right] \]

Prueba

Las partes (a) y (b) se desprenden de las propiedades de la función cuantil del alumno$ t_{n-1} $. Las partes (c) y (d) se derivan del hecho de que$ \frac{\sqrt{n - 1}}{\sigma} S $ tiene una distribución chi con$ n - 1 $ grados de libertad.

Una vez más, existe una compensación entre el nivel de confianza y la duración del intervalo de confianza. Si$n$ y$p$ son fijos, podemos disminuir$L$, y de ahí apretar nuestra estimación, sólo a costa de disminuir nuestra confianza en la estimación. Por el contrario, podemos aumentar nuestra confianza en la estimación sólo a expensas de aumentar la longitud del intervalo. En términos de$p$, el mejor de los intervalos de$1 - \alpha$ confianza de dos lados (y el que casi siempre se usa) es simétrico, igual al intervalo de cola con$ p = \frac{1}{2} $. Por último, señalar que realmente no tiene sentido considerar$ L $ como una función de$ S $, ya que$ S $ es una estadística más que una variable algebraica. De igual manera, no tiene sentido considerar$ L $ como una función de$ n $, ya que cambiar$ n $ significa nuevos datos y de ahí un nuevo valor de$ S $.

Utilice el experimento de estimación de medias para explorar el procedimiento. Seleccione la distribución normal y el$ T $ pivote. Utilice varios valores de parámetros, niveles de confianza, tamaños de muestra y tipos de intervalos. Para cada configuración, ejecute el experimento 1000 veces. A medida que se ejecuta la simulación, tenga en cuenta que el intervalo de confianza captura con éxito la media si y solo si el valor de la variable pivote está entre los cuantiles. Anote el tamaño y ubicación de los intervalos de confianza y compare la proporción de intervalos exitosos con el nivel de confianza teórico.

Intervalos de confianza para$ \sigma^2 $

A continuación construiremos intervalos de confianza para$ \sigma^2 $ usar la variable pivotante$ V $ dada anteriormente

Para$ \alpha \in (0, 1) $,

$\left[\frac{n - 1}{\chi^2_{n-1}\left(1 - \alpha / 2\right)} S^2,\frac{n - 1}{\chi^2_{n-1}\left(\alpha / 2\right)} S^2\right]$es un intervalo de$ 1 - \alpha $ confianza para$ \sigma^2 $
$\frac{n - 1}{\chi^2_{n-1}\left(1 - \alpha\right)} S^2$es un límite inferior de$ 1 - \alpha $ confianza para$ \sigma^2 $
$\frac{n - 1}{\chi^2_{n-1}(\alpha)} S^2$es un límite superior de$ 1 - \alpha $ confianza para$ \sigma^2 $.

Prueba

Dado que$ V = \frac{n - 1}{\sigma^2} S^2 $ tiene la distribución chi-cuadrada con$ n - 1 $ grados de libertad, cada uno de los siguientes eventos tiene probabilidad$ 1 - \alpha $ por definición de los cuantiles:

$ \left\{\chi^2_{n-1}(\alpha / 2) \le \frac{n - 1}{\sigma^2} S^2 \le \chi^2_{n-1}(1 - \alpha / 2)\right\} $
$ \left\{\frac{n - 1}{\sigma^2} S^2 \le \chi^2_{n-1}(1 - \alpha)\right\} $
$ \left\{\frac{n - 1}{\sigma^2} S^2 \ge \chi^2_{n-1}(\alpha)\right\} $

En cada caso, resolviendo$ \sigma^2 $ en la desigualdad dan el resultado.

Estas son las estimaciones de intervalos estándar para$ \sigma^2 $. El intervalo de dos lados en (a) es el intervalo de cola igual, correspondiente a la probabilidad$ \alpha / 2 $ en cada cola de la distribución de la variable pivote$ V $. Sin embargo, tenga en cuenta que este intervalo no es simétrico respecto a la varianza$ S^2 $ muestral Una vez más, podemos dividir la probabilidad$ \alpha $ entre las colas izquierda y derecha de la distribución de$ V $ cualquier manera que nos guste.

Para cada$ \alpha, \, p \in (0, 1) $, un intervalo de$ 1 - \alpha $ confianza para$ \sigma^2 $ es\[ \left[\frac{n - 1}{\chi^2_{n-1}(1 - p \alpha)} S^2, \frac{n - 1}{\chi^2_{n-1}(\alpha - p \alpha)} S^2\right]\]

$ p = \frac{1}{2} $da el intervalo de$ 1 - \alpha $ confianza de cola igual.
$ p \to 0 $da el intervalo con el límite$ 1 - \alpha $ superior
$ p \to 1 $da el intervalo con el límite$ 1 - \alpha $ inferior.

En cuanto a la distribución de la variable pivote$ V $, el intervalo de confianza anterior corresponde a$ p \alpha $ en la cola derecha y$ (1 - p) \alpha $ en la cola izquierda. Una vez más, veamos la longitud del intervalo de confianza general de dos lados. La longitud es aleatoria, pero es un múltiplo de la varianza de la muestra$ S^2 $. De ahí que podamos calcular el valor esperado y la varianza de la longitud.

Para$ \alpha, \, p \in (0, 1) $, la longitud (aleatoria) del intervalo de confianza de dos lados en el último teorema es\[ L = \left[\frac{1}{\chi^2_{n-1}(\alpha - p \alpha)} - \frac{1}{\chi^2_{n-1}(1 - p \alpha)}\right] (n - 1) S^2 \]

$ \E(L) = \left[\frac{1}{\chi^2_{n-1}(\alpha - p \alpha)} - \frac{1}{\chi^2_{n-1}(1 - p \alpha)}\right] (n - 1) \sigma^2 $
$\var(L) = 2 \left[\frac{1}{\chi^2_{n-1}(\alpha - p \alpha)} - \frac{1}{\chi^2_{n-1}(1 - p \alpha)}\right]^2 (n - 1) \sigma^4$

Para construir un intervalo de confianza óptimo de dos lados, sería natural encontrar$ p $ que minimice la longitud esperada. Este es un problema complicado, pero resulta que para grandes$ n $, el intervalo de cola igual con$ p = \frac{1}{2} $ está cerca de lo óptimo. Por supuesto, tomar raíces cuadradas de los puntos finales de cualquiera de los intervalos de confianza para$ \sigma^2 $ da intervalos de$ 1 - \alpha $ confianza para la desviación estándar de distribución$ \sigma $.

Utilice el experimento de estimación de varianza para explorar el procedimiento. Seleccione la distribución normal. Utilice varios valores de parámetros, niveles de confianza, tamaños de muestra y tipos de intervalos. Para cada configuración, ejecute el experimento 1000 veces. A medida que se ejecuta la simulación, tenga en cuenta que el intervalo de confianza captura con éxito la desviación estándar si y solo si el valor de la variable pivote está entre los cuantiles. Anote el tamaño y ubicación de los intervalos de confianza y compare la proporción de intervalos exitosos con el nivel de confianza teórico.

Conjuntos de confianza para$ (\mu, \sigma) $

En la discusión anterior, construimos intervalos de confianza para$ \mu $ y para$ \sigma $ por separado (nuevamente, generalmente ambos parámetros son desconocidos). En nuestra siguiente discusión, consideraremos conjuntos de confianza para el punto de parámetro$ (\mu, \sigma) $. Estos conjuntos serán subconjuntos del espacio de parámetros subyacente$ \R \times (0, \infty) $.

Conjuntos de confianza construidos a partir de las variables de pivote

Cada una de las variables de pivote$ Z $$ T $,, y se$ V $ puede utilizar para construir conjuntos de confianza para$ (\mu, \sigma) $. De forma aislada, cada uno producirá un conjunto de confianza sin límites, no es de extrañar ya que, estamos utilizando una única variable pivote para estimar dos parámetros. Consideramos$ Z $ primero la variable de pivote normal.

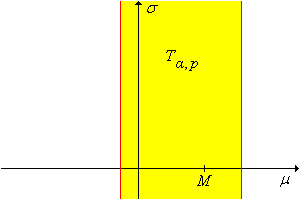
Para cualquier$\alpha, \, p \in (0, 1)$, un$1 - \alpha$ nivel de confianza establecido para$(\mu, \sigma)$ es\[ Z_{\alpha,p} = \left\{ (\mu, \sigma): M - z(1 - p \alpha) \frac{\sigma}{\sqrt{n}} \lt \mu \lt M - z(\alpha - p \alpha) \frac{\sigma}{\sqrt{n}} \right\} \] El conjunto de confianza es un cono en el espacio de$(\mu, \sigma)$ parámetros, con vértice en$(M, 0)$ y líneas límite de pendientes$-\sqrt{n} \big/ z(1 - p \alpha)$ y$-\sqrt{n} \big/ z(\alpha - p \alpha)$

Prueba

El cono de confianza se muestra en la gráfica siguiente. (Tenga en cuenta, sin embargo, que ambas pendientes pueden ser negativas o ambas positivas).

La variable pivote$T$ conduce al siguiente resultado:

Para cada$\alpha, \, p \in (0, 1)$, un$1 - \alpha$ nivel de confianza establecido para$(\mu, \sigma)$ es\[ T_{\alpha, p} = \left\{ (\mu, \sigma): M - t_{n-1}(1 - p \alpha) \frac{S}{\sqrt{n}} \lt \mu \lt M - t_{n-1}(\alpha - p \alpha) \frac{S}{\sqrt{n}} \right\}\]

Prueba

Por diseño, este conjunto de confianza no da información sobre$\sigma$. Finalmente, la variable pivote$V$ conduce al siguiente resultado:

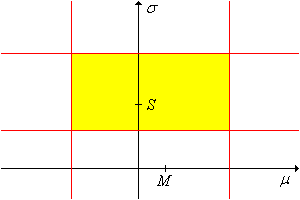
Para cada$\alpha, \, p \in (0, 1)$, un$1 - \alpha$ nivel de confianza establecido para$(\mu, \sigma)$ es\[ V_{\alpha, p} = \left\{ (\mu, \sigma): \frac{(n - 1)S^2}{\chi_{n-1}^2(1 - p \alpha)} \lt \sigma^2 \lt \frac{(n - 1)S^2}{\chi_{n-1}^2(\alpha - p \alpha)} \right\} \]

Prueba

Por diseño, este conjunto de confianza no da información sobre$\mu$.

Intersecciones

Ahora podemos formar intersecciones de algunos de los conjuntos de confianza construidos anteriormente para obtener conjuntos de confianza acotados para$(\mu, \sigma)$. Se utilizará el hecho de que la media muestral$M$ y la varianza muestral$S^2$ son independientes, una de las propiedades especiales más importantes de una muestra normal. También necesitaremos el resultado de la Introducción sobre la intersección de los interales de confianza. En los siguientes teoremas, supongamos que$\alpha, \, \beta, \, p, \, q \in (0, 1)$ con$\alpha + \beta \lt 1$.

El conjunto$T_{\alpha, p} \cap V_{\beta, q}$ es una$1 - (\alpha + \beta)$ confianza conservadora fija para$(\mu, \sigma)$.

El conjunto$Z_{\alpha, p} \cap V_{\beta, q}$ es un conjunto de$(1 - \alpha)(1 - \beta)$ confianza para$(\mu, \sigma)$.

Es interesante señalar que el conjunto de confianza$T_{\alpha, p} \cap V_{\beta, q}$ es un conjunto de productos como subconjunto del espacio de parámetros, pero no es un conjunto de productos como subconjunto del espacio de muestra. Por el contrario, el conjunto de confianza no$Z_{\alpha, p} \cap V_{\beta, q}$ es un conjunto de productos como subconjunto del espacio de parámetros, sino un conjunto de productos como un subconjunto del espacio de muestra.

Ejercicios

Robustez

El supuesto principal que hicimos fue que la distribución muestral subyacente es normal. Por supuesto, en problemas estadísticos reales, es poco probable que sepamos mucho sobre la distribución muestral, y mucho menos si es normal o no. Cuando un procedimiento estadístico funciona razonablemente bien, incluso cuando se violan los supuestos subyacentes, se dice que el procedimiento es robusto. En esta subsección, exploraremos la robustez de los procedimientos de estimación para$\mu$ y$\sigma$.

Supongamos de hecho que la distribución subyacente no es normal. Cuando el tamaño de la muestra$n$ es relativamente grande, la distribución de la media de la muestra seguirá siendo aproximadamente normal por el teorema del límite central. Por lo tanto, nuestras estimaciones de intervalos de aún$\mu$ pueden ser aproximadamente válidas.

Utilizar la simulación del experimento de estimación de medias para explorar el procedimiento. Seleccione la distribución gamma y seleccione el pivote del alumno. Utilice varios valores de parámetros, niveles de confianza, tamaños de muestra y tipos de intervalos. Para cada configuración, ejecute el experimento 1000 veces. Anote el tamaño y ubicación de los intervalos de confianza y compare la proporción de intervalos exitosos con el nivel de confianza teórico.

En el experimento de estimación de medias, repita el ejercicio previo con la distribución uniforme.

Lo grande que$n$ debe ser para que los procedimientos de estimación de$\mu$ intervalos funcionen bien depende, por supuesto, de la distribución subyacente; cuanto más se desvíe esta distribución de la normalidad, mayor$n$ debe ser. Afortunadamente, la convergencia a la normalidad en el teorema del límite central es rápida y por lo tanto, como observaste en los ejercicios, podemos salirnos con tamaños de muestra relativamente pequeños (30 o más) en la mayoría de los casos.

En general, los procedimientos de estimación de intervalos para no$\sigma$ son robustos; no existe un análogo del teorema del límite central que nos salve de las desviaciones de la normalidad.

En el experimento de estimación de varianza, seleccione la distribución gamma. Utilice varios valores de parámetros, niveles de confianza, tamaños de muestra y tipos de intervalos. Para cada configuración, ejecute el experimento 1000 veces. Anote el tamaño y ubicación de los intervalos de confianza y compare la proporción de intervalos exitosos con el nivel de confianza teórico.

En el experimento de estimación de varianza, seleccione la distribución uniforme. Utilice varios valores de parámetros, niveles de confianza, tamaños de muestra y tipos de intervalos. Para cada configuración, ejecute el experimento 1000 veces. Anote el tamaño y ubicación de los intervalos de confianza y compare la proporción de intervalos exitosos con el nivel de confianza teórico.

Ejercicios Computacionales

En los siguientes ejercicios, use la construcción de cola igual para intervalos de confianza de dos lados, a menos que se indique lo contrario.

Se supone que la longitud de cierta pieza mecanizada es de 10 centímetros pero debido a las imperfecciones en el proceso de fabricación, la longitud real se distribuye normalmente con media$\mu$ y varianza$\sigma^2$. La varianza se debe a factores inherentes al proceso, que se mantienen bastante estables a lo largo del tiempo. A partir de datos históricos, se sabe que$\sigma = 0.3$. Por otro lado, se$\mu$ puede establecer ajustando diversos parámetros en el proceso y por lo tanto puede cambiar a un valor desconocido con bastante frecuencia. Una muestra de 100 partes tiene media 10.2.

Construir el intervalo de confianza del 95% para$\mu$.
Construir el límite superior de confianza del 95% para$\mu$.
Construir el límite inferior de confianza del 95% para$\mu$.

Contestar

$(10.1, 10.26)$
10.25
10.15

Supongamos que el peso de una bolsa de papas fritas (en gramos) es una variable aleatoria normalmente distribuida con media$\mu$ y desviación estándar$\sigma$, ambas desconocidas. Una muestra de 75 bolsas tiene media 250 y desviación estándar 10.

Construir el intervalo de confianza del 90% para$\mu$.
Construir el intervalo de confianza del 90% para$\sigma$.
Construir un rectángulo conservador de confianza del 90% para$(\mu, \sigma)$.

Contestar

$(248.1, 251.9)$
$(8.8, 11.6)$
$(247.70, 252.30) \times (8.62, 11.92)$

En una empresa de telemarketing, la duración de una solicitud telefónica (en segundos) es una variable aleatoria normalmente distribuida con media$\mu$ y desviación estándar$\sigma$, ambas desconocidas. Una muestra de 50 llamadas tiene longitud media 300 y desviación estándar 60.

Construir el límite superior de confianza del 95% para$\mu$.
Construir el límite inferior de confianza del 95% para$\sigma$.

Contestar

314.3.
51.6.

En cierta granja el peso de un durazno (en onzas) en el momento de la cosecha es una variable aleatoria normalmente distribuida con desviación estándar 0.5. Cuántos melocotones deben muestrearse para estimar el peso medio con un margen de error$\pm 2$ y con 95% de confianza.

Contestar

El salario por hora para un determinado tipo de obra de construcción es una variable aleatoria normalmente distribuida con desviación estándar $1.25 y media desconocida$\mu$. ¿Cuántos trabajadores deben ser muestreados para construir un límite inferior de confianza del 95% para$\mu$ con margen de error de $0.25?

Contestar

Ejercicios de Análisis de Datos

En los datos de Michelson, se supone que la velocidad medida de la luz tiene una distribución normal con media$\mu$ y desviación estándar$\sigma$, ambas desconocidas.

Construir el intervalo de confianza del 95% para$\mu$. ¿Es el verdadero valor de la velocidad de la luz en este intervalo?
Construir el intervalo de confianza del 95% para$\sigma$.
Explorar, de manera gráfica informal, la suposición de que la distribución subyacente es normal.

Contestar

$(836.8, 868.0)$. No, el verdadero valor no está en el intervalo.
$(69.4, 91.8)$

En los datos de Cavendish, se supone que la densidad medida de la tierra tiene una distribución normal con media$\mu$ y desviación estándar$\sigma$, ambas desconocidas.

Construir el intervalo de confianza del 95% para$\mu$. ¿Está el verdadero valor de la densidad de la tierra en este intervalo?
Construir el intervalo de confianza del 95% para$\sigma$.
Explorar, de manera gráfica informal, la suposición de que la distribución subyacente es normal.

Contestar

$(5.364, 5.532)$. Sí, el valor verdadero está en el intervalo.
$(0.1725, 0.3074)$

En los datos de Short, se supone que el paralaje medido del sol tiene una distribución normal con media$\mu$ y desviación estándar$\sigma$, ambas desconocidas.

Construir el intervalo de confianza del 95% para$\mu$. ¿Es el verdadero valor del paralaje del sol en este intervalo?
Construir el intervalo de confianza del 95% para$\sigma$.
Explorar, de manera gráfica informal, la suposición de que la distribución subyacente es normal.

Contestar

$(8.410, 8.822)$. Sí, el valor verdadero está en el intervalo.
$(0.629, 0.927)$

Supongamos que la longitud de un pétalo de iris de un tipo dado (Setosa, Verginica o Versicolor) se distribuye normalmente. Utilice los datos del iris de Fisher para construir intervalos de confianza de dos lados del 90% para cada uno de los siguientes parámetros.

La longitud media de un pétalo de iris de Sertosa.
La longitud media de un pétalo de iris de Vergnica.
La longitud media de un pétalo de iris Versicolor.

Contestar

$(14.21, 15.03)$
$(54.21, 56.83)$
$(41.95, 44.49)$

Teoría Básica

El modelo normal

Intervalos de confianza para\( \mu \)\( \sigma \) con

Intervalos de confianza para\( \mu \) con\( \sigma \) desconocido

Intervalos de confianza para\( \sigma^2 \)

Conjuntos de confianza para\( (\mu, \sigma) \)

Conjuntos de confianza construidos a partir de las variables de pivote

Intersecciones

Ejercicios

Robustez

Ejercicios Computacionales

Ejercicios de Análisis de Datos