10.3: Triángulos Aleatorios

\(\newcommand{\P}{\mathbb{P}}\)\(\newcommand{\E}{\mathbb{E}}\)\(\newcommand{\var}{\text{var}}\)\(\newcommand{\R}{\mathbb{R}}\)\(\newcommand{\N}{\mathbb{N}}\)\(\newcommand{\area}{\text{area}}\)

Preliminares

Declaración del problema

Supongamos que un palo se rompe al azar en dos lugares. ¿Cuál es la probabilidad de que las tres piezas formen un triángulo?

Sin mirar a continuación, hacer una conjetura.

Ejecuta el experimento del triángulo 50 veces. No se preocupe por toda la información que se muestra en la aplicación, sino que solo tenga en cuenta si las piezas forman un triángulo. ¿Te gustaría revisar tu suposición?

Formulación Matemática

Como es habitual, el primer paso es modelar matemáticamente el experimento aleatorio. Tomaremos la longitud del palo como nuestra unidad de longitud, para que podamos identificar el palo con el intervalo\([0, 1]\). Para romper el palo en tres pedazos, solo necesitamos seleccionar dos puntos en el intervalo. Así, vamos a\(X\) denotar el primer punto elegido y\(Y\) el segundo punto elegido. Nótese que\(X\) y\(Y\) son variables aleatorias y de ahí que el espacio muestral de nuestro experimento sea\( S = [0, 1]^2 \). Ahora bien, para modelar la afirmación de que los puntos se eligen al azar, supongamos, como en las secciones anteriores, que\(X\) y\(Y\) son independientes y cada uno se distribuye uniformemente sobre\([0, 1]\).

El punto aleatorio\((X, Y)\) se distribuye uniformemente en\(S = [0, 1]^2\).

De ahí\[ \P\left[(X, Y) \in A\right] = \frac{\area(A)}{\area(S)} \]

Triángulos

La probabilidad de un triángulo

Las tres piezas forman un triángulo si y solo si las desigualdades del triángulo se mantienen: la suma de las longitudes de dos piezas cualesquiera debe ser mayor que la longitud de la tercera pieza.

El evento de que las piezas formen un triángulo es\(T_1 \cup T_2\) donde

1. \(T_1 = \left\{ (x, y) \in S: y \gt \frac{1}{2}, \; x \lt \frac{1}{2}, \; y - x \lt \frac{1}{2} \right\}\)
2. \(T_2 = \left\{ (x, y) \in S: x \gt \frac{1}{2}, \; y \lt \frac{1}{2}, \; x - y \lt \frac{1}{2} \right\}\)

A continuación\(T\) se presenta un boceto del evento. Curiosamente, ¡\(T\)se compone de triángulos!

Figura\(\PageIndex{1}\): El hecho de\( T = T_1 \cup T_2 \) que las piezas formen un triángulo

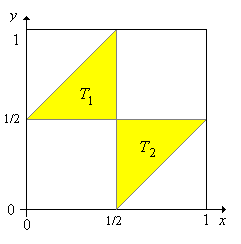
La probabilidad de que las piezas formen un triángulo es\(\P(T) = \frac{1}{4}\).

¿Qué tan cerca llegaste con tu suposición inicial? El valor relativamente bajo de\( \P(T) \) es un poco sorprendente.

Ejecutar el experimento del triángulo 1000 veces y comparar la probabilidad empírica de\(T^c\) a la probabilidad verdadera.

Triángulos de diferentes tipos

Ahora vamos a calcular la probabilidad de que las piezas formen un triángulo de un tipo dado. Recordemos que en un triángulo agudo los tres ángulos son menores de 90°, mientras que un triángulo obtuso tiene un ángulo (y solo uno) que es mayor a 90°. Un triángulo rectángulo, por supuesto, tiene un ángulo de 90°.

Supongamos que un triángulo tiene longitudes de lado\(a\)\(b\),, y\(c\), donde\(c\) es el más grande de estos. El triángulo es

1. aguda si y sólo si\(c^2 \lt a^2 + b^2\).
2. obtuso si y solo si\(c^2 \gt a^2 + b^2\).
3. derecho si y sólo si\(c^2 = a^2 + b^2\).

La parte (c), por supuesto, es el famoso teorema de Pitágoras, llamado así por el matemático griego antiguo Pitágoras.

Las ecuaciones del triángulo rectángulo para las piezas de palo son

1. \((y - x)^2 = x^2 + (1 - y)^2\)en\(T_1\)
2. \((1 - x)^2 = x^2 + (y - x)^2\)en\(T_1\)
3. \(x^2 = (y - x)^2 + (1 - y)^2\)en\(T_1\)
4. \((x - y)^2 = y^2 + (1 - x)^2\)en\(T_2\)
5. \((1 - x)^2 = y^2 + (x - y)^2\)en\(T_2\)
6. \(y^2 = (x - y)^2 + (1 - x)^2\)en\(T_2\)

Figura\(\PageIndex{2}\): Los eventos que las piezas forman triángulos agudos y obtusos

Dejar\(R\) denotar el evento de que las piezas forman un triángulo rectángulo. Entonces\(\P(R) = 0\).

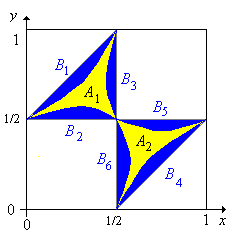
El evento de que las piezas formen un triángulo agudo es\(A = A_1 \cup A_2\) donde

1. \(A_1\)es la región dentro de las curvas (a), (b) y (c) de las ecuaciones del triángulo rectángulo.
2. \(A_2\)es la región dentro de las curvas (d), (e) y (f) de las ecuaciones del triángulo rectángulo.

El evento de que las piezas formen un triángulo obtuso es\(B = B_1 \cup B_2 \cup B_3 \cup B_4 \cup B_5 \cup B_6\) donde

1. \(B_1\),\(B_2\), y\(B_3\) son las regiones dentro\(T_1\) y fuera de las curvas (a), (b) y (c) de las ecuaciones del triángulo rectángulo, respectivamente.
2. \(B_4\),\(B_5\), y\(B_6\) son las regiones dentro\(T_2\) y fuera de las curvas (d), (e) y (f) de las ecuaciones del triángulo rectángulo, respectivamente.

La probabilidad de que las piezas formen un triángulo obtuso es\[ \P(B) = \frac{9}{4} - 3 \ln(2) \approx 0.1706 \]

Prueba

El cálculo simple demuestra que\(\P(B_i) = 3/8 - \ln(2) / 2\) para cada uno\(i \in \{1, 2, 3, 4, 5, 6\}\). Por ejemplo\ begin {align}\ P (B_1) & =\ int_0^ {1/2}\ frac {x\, (1 - 2\, x)} {2 - 2\, x}\, dx\\ P (B_3) & =\ int_0^ {1/2}\ left (y +\ frac {1} {2\, y} -\ frac {3} {2}\ derecha)\, dy\ end {align} De la simetría también se deduce que\(\P(B_i)\) es lo mismo para cada uno\(i\).

La probabilidad de que las piezas formen un triángulo agudo es\[ \P(A) = 3 \ln(2) - 2 \approx 0.07944 \]

Prueba

Tenga en cuenta que\(A \cup B \cup R = T\)\(A\), y\(B\), y\(R\) son disjuntas.

Ejecuta el experimento del triángulo 1000 veces y compara las probabilidades empíricas con las probabilidades verdaderas.