11.3: La distribución geométrica
- Page ID
- 151705
Teoría Básica
Definiciones
Supongamos nuevamente que nuestro experimento aleatorio consiste en realizar una secuencia de ensayos de Bernoulli\(\bs{X} = (X_1, X_2, \ldots)\) con parámetro de éxito\(p \in (0, 1]\). En esta sección estudiaremos la variable aleatoria\(N\) que da el número de prueba del primer éxito y la variable aleatoria\( M \) que da el número de fallas antes del primer éxito.
Dejar\( N = \min\{n \in \N_+: X_n = 1\} \), el número de prueba del primer éxito, y dejar\( M = N - 1 \), el número de fracasos antes del primer éxito. La distribución de\( N \) es la distribución geométrica en\( \N_+ \) y la distribución de\( M \) es la distribución geométrica en\( \N \). En ambos casos,\( p \) es el parámetro de éxito de la distribución.
Dado que\( N \) y\( M \) difieren por una constante, las propiedades de sus distribuciones son muy similares. Sin embargo, hay aplicaciones donde es más natural usar una que otra, y en la literatura, el término distribución geométrica puede referirse a cualquiera de las dos. En esta sección, nos concentraremos en la distribución de\( N \), haciendo una pausa ocasional para resumir los resultados correspondientes para\( M \).
La función de densidad de probabilidad
\( N \)tiene función de densidad de probabilidad\( f \) dada por\(f(n) = p (1 - p)^{n-1}\) for\(n \in \N_+\).
Prueba
Tenga en cuenta primero eso\(\{N = n\} = \{X_1 = 0, \ldots, X_{n-1} = 0, X_n = 1\}\). Por independencia, la probabilidad de este evento es\((1 - p)^{n-1} p\).
Comprobar que\( f \) es un PDF válido
Por resultados estándar para series geométricas\[\sum_{n=1}^\infty \P(N = n) = \sum_{n=1}^\infty (1 - p)^{n-1} p = \frac{p}{1 - (1 - p)} = 1\]
A priori, podríamos haber pensado que era posible tener\(N = \infty\) con probabilidad positiva; es decir, podríamos haber pensado que podríamos correr los juicios de Bernoulli para siempre sin ver nunca un éxito. Sin embargo, ahora sabemos que esto no puede suceder cuando el parámetro de éxito\(p\) es positivo.
La función de densidad de probabilidad de\(M\) viene dada por\(\P(M = n) = p (1 - p)^n\) for\( n \in \N\).
En el experimento binomial negativo, se establece\(k = 1\) para obtener la distribución geométrica\(\N_+\). Varíe\(p\) con la barra de desplazamiento y anote la forma y ubicación de la función de densidad de probabilidad. Para valores seleccionados de\(p\), ejecute la simulación 1000 veces y compare la función de frecuencia relativa con la función de densidad de probabilidad.
Tenga en cuenta que las funciones de densidad de probabilidad de\( N \) y\( M \) están disminuyendo, y por lo tanto tienen modos en 1 y 0, respectivamente. La forma geométrica de las funciones de densidad de probabilidad también explica el término distribución geométrica.
Funciones de distribución y la propiedad sin memoria
Supongamos que\( T \) es una variable aleatoria tomando valores en\( \N_+ \). Recordemos que la función de distribución ordinaria de\( T \) es la función\( n \mapsto \P(T \le n) \). En esta sección, la función complementaria\( n \mapsto \P(T \gt n) \) jugará un papel fundamental. Nos referiremos a esta función como la función de distribución correcta de\( T \). Por supuesto ambas funciones determinan completamente la distribución de\( T \). Supongamos nuevamente que\( N \) tiene la distribución geométrica encendida\( \N_+ \) con parámetro de éxito\( p \in (0, 1] \).
\( N \)tiene función de distribución correcta\( G \) dada por\(G(n) = (1 - p)^n\) for\(n \in \N\).
Prueba de los juicios de Bernoulli
Tenga en cuenta que\(\{N \gt n\} = \{X_1 = 0, \ldots, X_n = 0\}\). Por independencia, la probabilidad de este evento es\((1 - p)^n\).
Prueba directa
Usando series geométricas,\[ \P(N \gt n) = \sum_{k=n+1}^\infty \P(N = k) = \sum_{k=n+1}^\infty (1 - p)^{k-1} p = \frac{p (1 - p)^n}{1 - (1 - p)} = (1 - p)^n \]
Del último resultado, se deduce que la función de distribución ordinaria (izquierda) de\(N\) es dada por Ahora\[ F(n) = 1 - (1 - p)^n, \quad n \in \N \] exploraremos otra caracterización conocida como la propiedad sin memoria.
Para\( m \in \N \), la distribución condicional de\(N - m\) dado\(N \gt m\) es la misma que la distribución de\(N\). Es decir,\[\P(N \gt n + m \mid N \gt m) = \P(N \gt n); \quad m, \, n \in \N\]
Prueba
Del resultado anterior y de la definición de probabilidad condicional,\[ \P(N \gt n + m \mid N \gt m) = \frac{\P(N \gt n + m)}{\P(N \gt m)} = \frac{(1 - p)^{n+m}}{(1 - p)^m} = (1 - p)^n = \P(N \gt n)\]
Así, si el primer éxito no ha ocurrido por número de ensayo\(m\), entonces el número restante de ensayos necesarios para lograr el primer éxito tiene la misma distribución que el número de prueba del primer éxito en una nueva secuencia de ensayos de Bernoulli. En definitiva, los juicios de Bernoulli no tienen memoria. Este hecho tiene implicaciones para un jugador que apuesta en los ensayos de Bernoulli (como en los juegos de casino ruleta o dados). Ninguna estrategia de apuestas basada en observaciones de resultados pasados de las pruebas posiblemente pueda ayudar al jugador.
Por el contrario, si\(T\) es una variable aleatoria tomando valores en\(\N_+\) que satisface la propiedad sin memoria, entonces\(T\) tiene una distribución geométrica.
Prueba
Dejemos\(G(n) = \P(T \gt n)\) para\(n \in \N\). La propiedad sin memoria y la definición de probabilidad condicional implican que\(G(m + n) = G(m) G(n)\) para\(m, \; n \in \N\). Tenga en cuenta que esta es la ley de exponentes para\(G\). De ello se deduce que\(G(n) = G^n(1)\) para\(n \in \N\). De ahí\(T\) que tenga la distribución geométrica con parámetro\(p = 1 - G(1)\).
Momentos
Supongamos nuevamente que\(N\) es el número de prueba del primer éxito en una secuencia de ensayos de Bernoulli, de manera que\(N\) tiene la distribución geométrica\(\N_+\) con parámetro\(p \in (0, 1]\). La media y varianza de se\(N\) pueden calcular de varias maneras diferentes.
\(\E(N) = \frac{1}{p}\)
Prueba de la función de densidad
Usando la derivada de la serie geométrica,\ begin {align}\ E (N) &=\ sum_ {n=1} ^\ infty n p (1 - p) ^ {n-1} = p\ sum_ {n=1} ^\ infty n (1 - p) ^ {n-1}\\ &= p\ sum_ {n=1} ^\ infty -\ frac {d} {dp} (1 - p) ^n = - p\ frac {d} {d p}\ sum_ {n=0} ^\ infty (1 - p) ^n\\ &= -p\ frac {d} {dp}\ frac {1} {p} = -p\ izquierda (-\ frac {1} {p^2}\ derecha) =\ frac {1} {p}\ end {align}
Prueba de la función de distribución correcta
Recordemos que dado que\( N \) toma valores enteros positivos, su valor esperado puede calcularse como la suma de la función de distribución correcta. De ahí\[ \E(N) = \sum_{n=0}^\infty \P(N \gt n) = \sum_{n=0}^\infty (1 - p)^n = \frac{1}{p} \]
Prueba de los juicios de Bernoulli
Acondicionamos en el primer juicio\( X_1 \): Si\( X_1 = 1 \) entonces\( N = 1 \) y por lo tanto\( \E(N \mid X_1 = 1) = 1 \). Si\( X_1 = 0 \) (equivalentemente\( N \gt 1) \) entonces por la propiedad sin memoria,\( N - 1 \) tiene la misma distribución que\( N \). De ahí\( \E(N \mid X_1 = 0) = 1 + \E(N) \). En definitiva\[ \E(N \mid X_1) = 1 + (1 - X_1) \E(N) \] se deduce que\[ \E(N) = \E\left[\E(N \mid X_1)\right] = 1 + (1 - p) \E(N)\] Resolver da\( \E(N) = \frac{1}{p}\).
Este resultado tiene sentido intuitivo. En una secuencia de ensayos de Bernoulli con parámetro de éxito\( p \) esperaríamos
esperar\( 1/p \) ensayos para el primer éxito.
\( \var(N) = \frac{1 - p}{p^2} \)
Prueba directa
Primero calculamos\( \E\left[N(N - 1)\right] \). Este es un ejemplo de un momento factorial, y calcularemos los momentos factoriales generales a continuación. Usando de nuevo derivadas de la serie geométrica,\ begin {align}\ E\ left [N (N - 1)\ right] & =\ sum_ {n=2} ^\ infty n (n - 1) p (1 - p) ^ {n-1} = p (1 - p)\ sum_ {n=2} ^\ infty n (n - 1) (1 - p) ^ {n-2}\ & = p (1 - p)\ frac {d^2} {d p^2}\ suma_ {n=0} ^\ infty (1 - p) ^n = p (1 - p)\ frac {d^2} {dp^2}\ frac {1} {p} = p (1 - p)\ frac {2} {p^3} = 2\ frac {1 - p} {p^2}\ end {align} Ya que\( \E(N) = \frac{1}{p} \), se deduce que\( \E\left(N^2\right) = \frac{2 - p}{p^2} \) y por lo tanto\( \var(N) = \frac{1 - p}{p^2} \)
Prueba de los juicios de Bernoulli
Recordemos eso\[ \E(N \mid X_1) = 1 + (1 - X_1) \E(N) = 1 + \frac{1}{p} (1 - X_1) \] y por el mismo razonamiento,\( \var(N \mid X_1) = (1 - X_1) \var(N) \). De ahí\[ \var(N) = \var\left[\E(N \mid X_1)\right] + \E\left[\var(N \mid X_1)\right] = \frac{1}{p^2} p(1 - p) + (1 - p) \var(N) \] Resolver da\( \var(N) = \frac{1 - p}{p^2} \).
Tenga en cuenta que\( \var(N) = 0 \) si\( p = 1 \), apenas sorprende ya que\( N \) es determinista (tomando solo el valor 1) en este caso. En el otro extremo,\( \var(N) \uparrow \infty \) como\( p \downarrow 0 \).
En el experimento binomial negativo, establecer\(k = 1\) para obtener la distribución geométrica. Varíe\(p\) con la barra de desplazamiento y anote la ubicación y el tamaño de la barra de desviación\(\pm\) estándar media. Para los valores seleccionados de\(p\), ejecute la simulación 1000 veces y compare la media de la muestra y la desviación estándar con la media de distribución y la desviación estándar.
la función de generación de probabilidad\( P \) de\(N\) viene dada por\[ P(t) = \E\left(t^N\right) = \frac{p t}{1 - (1 - p) t}, \quad \left|t\right| \lt \frac{1}{1 - p} \]
Prueba
Este resultado se desprende de otra aplicación más de las series geométricas:\[ \E\left(t^N\right) = \sum_{n=1}^\infty t^n p (1 - p)^{n-1} = p t \sum_{n=1}^\infty \left[t (1 - p)\right]^{n-1} = \frac{p t}{1 - (1 - p) t}, \quad \left|(1 - p) t\right| \lt 1 \]
Recordemos de nuevo que para\( x \in \R \) y\( k \in \N \), el poder descendente\( x \) del orden\( k \) es\( x^{(k)} = x (x - 1) \cdots (x - k + 1) \). Si\( X \) es una variable aleatoria, entonces\( \E\left[X^{(k)}\right] \) es el momento factorial\( X \) de orden\( k \).
Los momentos factoriales de\(N\) están dados por\[ \E\left[N^{(k)}\right] = k! \frac{(1 - p)^{k-1}}{p^k}, \quad k \in \N_+ \]
Prueba de series geométricas
Usando de nuevo derivadas de series geométricas,\ begin {align}\ E\ left [N^ {(k)}\ right] & =\ sum_ {n=k} ^\ infty n^ {(k)} p (1 - p) ^ {n-1} = p (1 - p) ^ {k-1}\ sum_ {n=k} ^\ infty n^ {(k)} (1 - p) ^ {n-k}\\ & = p (1 - p) ^ {k-1} (-1) ^k\ frac {d^k} {dp^k}\ sum_ {n=0} ^\ infty (1 - p) ^n = p (1 - p) ^ {k-1} (-1) ^k\ frac {d^k} {dp^k}\ frac {1} {p} = k! \ frac {(1 - p) ^ {k-1}} {p^k}\ end {align}
Prueba de la función generadora
Recordemos que\(\E\left[N^{(k)}\right] = P^{(k)}(1)\) donde\(P\) está la función generadora de probabilidad de\(N\). Por lo que el resultado se desprende del cálculo estándar.
Supongamos que\( p \in (0, 1) \). La asimetría y curtosis\(N\) de
- \(\skw(N) = \frac{2 - p}{\sqrt{1 - p}}\)
- \(\kur(N) = \frac{p^2}{1 - p}\)
Prueba
Los momentos factoriales se pueden utilizar para encontrar los momentos de\(N\) aproximadamente 0. Los resultados luego se derivan de las fórmulas computacionales estándar para asimetría y curtosis.
Tenga en cuenta que la distribución geométrica siempre está sesgada positivamente. Por otra parte,\( \skw(N) \to \infty \) y\( \kur(N) \to \infty \) como\( p \uparrow 1 \).
Supongamos ahora eso\(M = N - 1\), para que\(M\) (el número de fracasos antes del primer éxito) tenga la distribución geométrica encendida\(\N\). Entonces
- \(\E(M) = \frac{1 - p}{p}\)
- \(\var(M) = \frac{1 - p}{p^2}\)
- \(\skw(M) = \frac{2 - p}{\sqrt{1 - p}}\)
- \(\kur(M) = \frac{p^2}{1 - p}\)
- \(\E\left(t^M\right) = \frac{p}{1 - (1 - p) \, t}\)para\(\left|t\right| \lt \frac{1}{1 - p}\)
Por supuesto, el hecho de que la varianza, asimetría y curtosis no se hayan modificado sigue fácilmente, ya que\(N\) y\(M\) difieren por una constante.
La función cuantil
Dejar\(F\) denotar la función de distribución de\(N\), de modo que\(F(n) = 1 - (1 - p)^n\) para\(n \in \N\). Recordemos que\(F^{-1}(r) = \min \{n \in \N_+: F(n) \ge r\}\) para\(r \in (0, 1)\) es la función cuantil de\(N\).
La función cuantil de\(N\) es\[ F^{-1}(r) = \left\lceil \frac{\ln(1 - r)}{\ln(1 - p)}\right\rceil, \quad r \in (0, 1) \]
Por supuesto, la función cuantil, al igual que la función de densidad de probabilidad y la función de distribución, determina completamente la distribución de\(N\). Además, podemos calcular la mediana y los cuartiles para obtener medidas de centro y propagación.
El primer cuartil, la mediana (o segundo cuartil) y el tercer cuartil son
- \(F^{-1}\left(\frac{1}{4}\right) = \left\lceil \ln(3/4) \big/ \ln(1 - p)\right\rceil \approx \left\lceil-0.2877 \big/ \ln(1 - p)\right\rceil\)
- \(F^{-1}\left(\frac{1}{2}\right) = \left\lceil \ln(1/2) \big/ \ln(1 - p)\right\rceil \approx \left\lceil-0.6931 \big/ \ln(1 - p)\right\rceil\)
- \(F^{-1}\left(\frac{3}{4}\right) = \left\lceil \ln(1/4) \big/ \ln(1 - p)\right\rceil \approx \left\lceil-1.3863 \big/ \ln(1 - p)\right\rceil\)
Abra la calculadora de distribución especial y seleccione la distribución geométrica y la vista CDF. Varíe\( p \) y anote la forma y ubicación de la función CDF/cuantil. Para diversos valores de\( p \), computar la mediana y el primer y tercer cuartiles.
La propiedad de tasa constante
Supongamos que\(T\) es una variable aleatoria que toma valores\(\N_+\), los cuales interpretamos como la primera vez que ocurre algún evento de interés.
La función\( h \) dada por\[ h(n) = \P(T = n \mid T \ge n) = \frac{\P(T = n)}{\P(T \ge n)}, \quad n \in \N_+ \] es la función de tasa de\(T\).
Si\(T\) se interpreta como la vida útil (discreta) de un dispositivo, entonces\(h\) es una versión discreta de la función de tasa de fallas estudiada en la teoría de la confiabilidad. Sin embargo, en nuestra formulación habitual de los ensayos de Bernoulli, el evento de interés es el éxito más que el fracaso (o la muerte), por lo que simplemente usaremos el término función de tasa para evitar confusiones. La propiedad de tasa constante caracteriza la distribución geométrica. Como es habitual, vamos a\(N\) denotar el número de prueba del primer éxito en una secuencia de ensayos de Bernoulli con parámetro de éxito\(p \in (0, 1)\), de manera que\(N\) tiene la distribución geométrica en\(\N_+\) con parámetro\(p\).
\(N\)tiene tasa constante\(p\).
Prueba
De los resultados anteriores,\( \P(N = n) = p (1 - p)^{n-1} \) y\( \P(N \ge n) = \P(N \gt n - 1) = (1 - p)^{n-1} \), así\( \P(N = n) \big/ \P(N \ge n) = p \) para\( n \in \N_+ \).
Por el contrario, si\(T\) tiene tasa constante\(p \in (0, 1)\) entonces\(T\) tiene el parámetro de distrbución geométrica\(\N_+\) con éxito\(p\).
Prueba
Dejemos\(H(n) = \P(T \ge n)\) para\(n \in \N_+\). A partir de la propiedad de tasa constante,\(\P(T = n) = p \, H(n)\) para\(n \in \N_+\). Siguiente nota que\(\P(T = n) = H(n) - H(n + 1)\) para\(n \in \N_+\). Así,\(H\) satisface la relación de recurrencia\(H(n + 1) = (1 - p) \, H(n)\) para\(n \in \N_+\). También\(H\) satisface la condición inicial\(H(1) = 1\). Resolver la relación de recurrencia da\(H(n) = (1 - p)^{n-1}\) para\(n \in \N_+\).
Relación con la Distribución Uniforme
Supongamos nuevamente que\( \bs{X} = (X_1, X_2, \ldots) \) es una secuencia de ensayos de Bernoulli con parámetro de éxito\( p \in (0, 1) \). Para\( n \in \N_+ \), recordemos que\(Y_n = \sum_{i=1}^n X_i\), el número de éxitos en los primeros\(n\) ensayos, tiene la distribución binomial con parámetros\(n\) y\(p\). Como antes,\( N \) denota el número de prueba del primer éxito.
Supongamos que\( n \in \N_+ \). La distribución condicional de\(N\) dado\(Y_n = 1\) es uniforme en\(\{1, 2, \ldots, n\}\).
Prueba de muestreo
Mostramos en la última sección que dado\( Y_n = k \), los números de prueba de los éxitos forman una muestra aleatoria de tamaño\( k \) elegido sin reemplazo de\( \{1, 2, \ldots, n\} \). Este resultado es un simple corolario con\( k = 1 \)
Prueba directa
Para\( j \in \{1, 2, \ldots, n\} \)\[ \P(N = j \mid Y_n = 1) = \frac{\P(N = j, Y_n = 1)}{\P(Y_n = 1)} = \frac{\P\left(Y_{j-1} = 0, X_j = 1, Y_{n} - Y_j = 0\right)}{\P(Y_n = 1)} \] En palabras, los acontecimientos en el numerador de la última fracción son que no hay éxitos en los primeros\( j - 1 \) ensayos, un éxito en juicio\( j \), y no hay éxitos en ensayos\( j + 1 \) a\( n \). Estos eventos son independientes\[ \P(N = j \mid Y_n = 1) = \frac{(1 - p)^{j-1} p (1 - p)^{n-j}}{n p (1 - p)^{n - 1}} = \frac{1}{n}\]
Tenga en cuenta que la distribución condicional no depende del parámetro de éxito\(p\). Si sabemos que hay exactamente un éxito en los primeros\(n\) juicios, entonces es igualmente probable que el número de prueba de ese éxito sea cualquiera de las\(n\) posibilidades.
Otra conexión entre la distribución geométrica y la distribución uniforme se da a continuación en el juego alternante de lanzamiento de monedas: la distribución condicional de\( N \) dado\( N \le n \) converge a la distribución uniforme en\( \{1, 2, \ldots, n\} \) as\( p \downarrow 0 \).
Relación con la Distribución Exponencial
El proceso de Poisson on\( [0, \infty) \), llamado así por Simeon Poisson, es un modelo para puntos aleatorios en tiempo continuo. Hay muchas conexiones profundas e interesantes entre el proceso de ensayos de Bernoulli (que se puede considerar como un modelo para puntos aleatorios en tiempo discreto) y el proceso de Poisson. Estas conexiones se exploran en detalle en el capítulo sobre el proceso de Poisson. En esta sección solo damos el resultado más famoso e importante: la convergencia de la distribución geométrica a la distribución exponencial. La distribución geométrica, como sabemos, gobierna el tiempo del primer punto aleatorio
en el proceso de ensayos de Bernoulli, mientras que la distribución exponencial gobierna el tiempo del primer punto aleatorio en el proceso de Poisson.
Como referencia, la distribución exponencial con parámetro de tasa\( r \in (0, \infty) \) tiene función de distribución\( F(x) = 1 - e^{-r x} \) para\( x \in [0, \infty) \). La media de la distribución exponencial es\( 1 / r \) y la varianza es\( 1 / r^2 \). Además, la función de generación de momento es\( s \mapsto \frac{1}{s - r} \) para\( s \gt r \).
Para\( n \in \N_+ \), supongamos que\( U_n \) tiene la distribución geométrica\( \N_+ \) encendida con parámetro de éxito\( p_n \in (0, 1) \), donde\( n p_n \to r \gt 0 \) como\( n \to \infty \). Entonces la distribución de\( U_n / n \) converge a la distribución exponencial con parámetro\( r \) as\( n \to \infty \).
Prueba
Vamos a\( F_n \) denotar el CDF de\( U_n / n \). Entonces para\( x \in [0, \infty) \)\[ F_n(x) = \P\left(\frac{U_n}{n} \le x\right) = \P(U_n \le n x) = \P\left(U_n \le \lfloor n x \rfloor\right) = 1 - \left(1 - p_n\right)^{\lfloor n x \rfloor} \] Pero por un famoso límite del cálculo,\( \left(1 - p_n\right)^n = \left(1 - \frac{n p_n}{n}\right)^n \to e^{-r} \) como\( n \to \infty \), y por lo tanto\( \left(1 - p_n\right)^{n x} \to e^{-r x} \) como\( n \to \infty \). Pero por definición,\( \lfloor n x \rfloor \le n x \lt \lfloor n x \rfloor + 1\) o equivalentemente,\( n x - 1 \lt \lfloor n x \rfloor \le n x \) por lo que se deduce que\( \left(1 - p_n \right)^{\lfloor n x \rfloor} \to e^{- r x} \) como\( n \to \infty \). De ahí\( F_n(x) \to 1 - e^{-r x} \) as\( n \to \infty \), que es el CDF de la distribución exponencial.
Obsérvese que la condición\( n p_n \to r \) como\( n \to \infty \) es la misma condición requerida para la convergencia de la distribución binomial al Poisson que estudiamos en la última sección.
Familias Especiales
La distribución geométrica on\( \N \) es una distribución infinitamente divisible y es una distribución compuesta de Poisson. Para conocer los detalles, visite estas secciones individuales y vea la siguiente sección sobre la distribución binomial negativa.
Ejemplos y Aplicaciones
Ejercicios simples
Se lanza un dado estándar y justo hasta que se produce un as. Vamos a\(N\) denotar el número de lanzamientos. Encuentra cada uno de los siguientes:
- La función de densidad de probabilidad de\(N\).
- La media de\(N\).
- La varianza de\(N\).
- La probabilidad de que el dado tenga que ser arrojado al menos 5 veces.
- La función cuantil de\(N\).
- La mediana y el primer y tercer cuartiles.
Contestar
- \(\P(N = n) = \left(\frac{5}{6}\right)^{n-1} \frac{1}{6}\)para\( n \in \N_+\)
- \(\E(N) = 6\)
- \(\var(N) = 30\)
- \(\P(N \ge 5) = 525 / 1296\)
- \(F^{-1}(r) = \lceil \ln(1 - r) / \ln(5 / 6)\rceil\)para\( r \in (0, 1)\)
- Cuartiles\(q_1 = 2\),\(q_2 = 4\),\(q_3 = 8\)
Un tipo de misil tiene probabilidad de falla 0.02. Vamos a\(N\) denotar el número de lanzamientos antes de la primera falla. Encuentra cada uno de los siguientes:
- La función de densidad de probabilidad de\(N\).
- La media de\(N\).
- La varianza de\(N\).
- La probabilidad de 20 lanzamientos exitosos consecutivos.
- La función cuantil de\(N\).
- La mediana y el primer y tercer cuartiles.
Contestar
- \(\P(N = n) \ \left(\frac{49}{50}\right)^{n-1} \frac{1}{50}\)para\( n \in \N_+\)
- \(\E(N) = 50\)
- \(\var(N) = 2450\)
- \(\P(N \gt 20) = 0.6676\)
- \(F^{-1}(r) = \lceil \ln(1 - r) / \ln(0.98)\rceil\)para\( r \in (0, 1)\)
- Cuartiles\(q_1 = 15\),\(q_2 = 35\),\(q_3 = 69\)
Un estudiante realiza una prueba de opción múltiple con 10 preguntas, cada una con 5 opciones (solo una correcta). El estudiante adivina ciegamente y obtiene una pregunta correcta. Encuentra la probabilidad de que la pregunta correcta sea una de las primeras 4.
Contestar
0.4
Recordemos que una rueda de ruleta americana tiene 38 ranuras: 18 son rojas, 18 son negras y 2 son verdes. Supongamos que observa rojo o verde en 10 giros consecutivos. Dar la distribución condicional del número de giros adicionales necesarios para que ocurra el negro.
Contestar
Geométrico con\(p = \frac{18}{38}\)
El juego de la ruleta se estudia con más detalle en el capítulo de Juegos de azar.
En el experimento binomial negativo, conjunto\(k = 1\) para obtener la distribución geométrica y conjunto\(p = 0.3\). Ejecutar el experimento 1000 veces. Calcular las frecuencias relativas apropiadas e investigar empíricamente la propiedad sin memoria\[ \P(V \gt 5 \mid V \gt 2) = \P(V \gt 3) \]
El problema de Petersburgo
Ahora exploraremos una situación de juego, conocida como el problema de Petersburgo, que lleva a algunos resultados famosos y sorprendentes. Supongamos que estamos apostando por una secuencia de ensayos de Bernoulli con parámetro de éxito\(p \in (0, 1)\). Podemos apostar cualquier cantidad de dinero en un juicio en apuestas pares: si el ensayo resulta en éxito, recibimos esa cantidad, y si el juicio resulta en fracaso, debemos pagar esa cantidad. Utilizaremos la siguiente estrategia, conocida como estrategia martingala:
- Apostamos\(c\) unidades en el primer trial.
- Siempre que perdemos un juicio, doblamos la apuesta para el siguiente juicio.
- Paramos en cuanto ganamos un juicio.
Vamos a\( N \) denotar el número de ensayos jugados, así que eso\( N \) tiene la distribución geométrica con parámetro\( p \), y vamos\( W \) denotar nuestras ganancias netas cuando nos detenemos.
\(W = c\)
Prueba
El primer triunfo ocurre en el juicio\(N\), por lo que la apuesta inicial se duplicó\(N - 1\) veces. Las ganancias netas son\[W = -c \sum_{i=0}^{N-2} 2^i + c 2^{N-1} = c\left(1 - 2^{N-1} + 2^{N-1}\right) = c\]
Así, ¡no\(W\) es aleatorio y\(W\) es independiente de\(p\)! Ya que\(c\) es una constante arbitraria, parecería que tenemos una estrategia ideal. No obstante, estudiemos la cantidad de dinero\(Z\) necesaria para jugar la estrategia.
\(Z = c (2^N - 1)\)
La cantidad esperada de dinero que se necesita para la estrategia martingala es\[ \E(Z) = \begin{cases} \frac{c}{2 p - 1}, & p \gt \frac{1}{2} \\ \infty, & p \le \frac{1}{2} \end{cases} \]
Así, la estrategia es fatalmente defectuosa cuando los juicios son desfavorables e incluso cuando son justos, ya que necesitamos un capital infinito esperado para que la estrategia funcione en estos casos.
Calcular\(\E(Z)\) explícitamente si\(c = 100\) y\(p = 0.55\).
Contestar
$1000
En el experimento binomial negativo, conjunto\(k = 1\). Para cada uno de los siguientes valores de\(p\), ejecutar el experimento 100 veces. Para cada ejecución computar\(Z\) (con\(c = 1\)). Encuentra el valor promedio de\(Z\) más de las 100 corridas:
- \(p = 0.2\)
- \(p = 0.5\)
- \(p = 0.8\)
Para obtener más información sobre estrategias de juego, consulte la sección sobre Rojo y Negro. Las martingales se estudian en detalle en un capítulo separado.
El juego alternante de lanzamiento de monedas
Una moneda tiene probabilidad de cabezas\(p \in (0, 1]\). Hay\(n\) jugadores que se turnan lanzando la moneda al estilo round robin: primero el jugador 1, luego el jugador 2, continuando hasta el jugador\(n\), luego el jugador 1 nuevamente, y así sucesivamente. El primer jugador en lanzar cabezas gana el juego.
Vamos a\(N\) denotar el número del primer lanzamiento que resulta en cabezas. Por supuesto,\(N\) tiene la distribución geométrica encendida\(\N_+\) con parámetro\(p\). Adicionalmente, vamos a\(W\) denotar al ganador del juego;\(W\) toma valores en el set\(\{1, 2, \ldots, n\}\). Nos interesa la distribución de probabilidad de\(W\).
Para\(i \in \{1, 2, \ldots, n\}\),\(W = i\) si y solo si\(N = i + k n\) para algunos\(k \in \N\). Es decir, usando aritmética modular,\[ W = [(N - 1) \mod n] + 1 \]
El jugador ganador\(W\) tiene función de densidad de probabilidad\[ \P(W = i) = \frac{p (1 - p)^{i-1}}{1 - (1 - p)^n}, \quad i \in \{1, 2, \ldots, n\} \]
Prueba
Esto se desprende del ejercicio anterior y la distribución geométrica de\(N\).
\(\P(W = i) = (1 - p)^{i-1} \P(W = 1)\)para\(i \in \{1, 2, \ldots, n\}\).
Prueba
Este resultado se puede argumentar directamente, utilizando la propiedad sin memoria de la distribución geométrica. Para\(i\) que el jugador gane, los\(i - 1\) jugadores anteriores deben primero todos tirar colas. Entonces, el jugador\(i\) efectivamente se convierte en el primer jugador en una nueva secuencia de tiradas. Este resultado se puede utilizar para dar otra derivación de la función de densidad de probabilidad en el ejercicio anterior.
Tenga en cuenta que\(\P(W = i)\) es una función decreciente de\(i \in \{1, 2, \ldots, n\}\). No en vano, cuanto menor sea el orden de lanzamiento mejor para el jugador.
Calcular explícitamente la función de densidad de probabilidad de\(W\) cuando la moneda es justa (\(p = 1 / 2\)).
Contestar
\(\P(W = i) = 2^{n-1} \big/ (2^n - 1), \quad i \in \{1, 2, \ldots, n\}\)
Observe del resultado anterior que\(W\) en sí tiene una distribución geométrica truncada.
La distribución de\(W\) es la misma que la distribución condicional de\(N\) dado\(N \le n\):\[ \P(W = i) = \P(N = i \mid N \le n), \quad i \in \{1, 2, \ldots, n\} \]
Los siguientes problemas exploran algunas distribuciones limitantes relacionadas con el juego alternante de lanzamiento de monedas.
Para fijo\(p \in (0, 1]\), la distribución de\(W\) converge a la distribución geométrica con parámetro\(p\) as\(n \uparrow \infty\).
Para fijo\(n\), la distribución de\(W\) converge a la distribución uniforme en\(\{1, 2, \ldots, n\}\) as\(p \downarrow 0\).
Los jugadores al final de la orden de lanzamiento deben esperar una moneda sesgada hacia las colas.
Hombre extraño
En el juego de odd man out, comenzamos con un número determinado de jugadores, cada uno con una moneda que tiene la misma probabilidad de cabezas. Los jugadores lanzan sus monedas al mismo tiempo. Si hay un hombre extraño, es decir, un jugador con un resultado diferente al de todos los demás jugadores, entonces el jugador impar es eliminado; de lo contrario, ningún jugador es eliminado. En cualquier caso, los jugadores restantes continúan el juego de la misma manera. Un ligero problema técnico surge con solo dos jugadores, ya que diferentes resultados harían que ambos jugadores fueran extraños
. Entonces en este caso, podríamos (arbitrariamente) hacer del jugador con colas el hombre impar.
Supongamos que hay\(k \in \{2, 3, \ldots\}\) jugadores y\(p \in [0, 1]\). En una sola ronda, la probabilidad de un hombre impar es\[r_k(p) = \begin{cases} 2 p (1 - p), & k = 2 \\ k p (1 - p)^{k-1} + k p^{k-1} (1 - p), & k \in \{3, 4, \ldots\} \end{cases}\]
Prueba
Vamos a\(Y\) denotar el número de cabezas. Si\(k = 2\), el suceso de que hay un hombre extraño es\(\{Y = 1\}\). Si\(k \ge 3\), el suceso de que hay un hombre extraño es\(\{Y \in \{1, k - 1\}\}\). El resultado ahora sigue ya que\(Y\) tiene una distribución binomial con parámetros\( k \) y\( p \).
La gráfica de\(r_k\) es más interesante de lo que piensas.
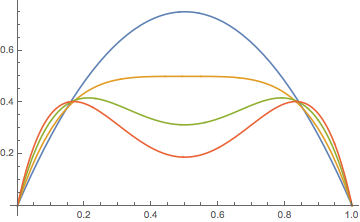
Para\( k \in \{2, 3, \ldots\} \),\(r_k\) cuenta con las siguientes propiedades:
- \(r_k(0) = r_k(1) = 0\)
- \(r_k\)es simétrico sobre\(p = \frac{1}{2}\)
- Para fijo\(p \in [0, 1]\),\(r_k(p) \to 0\) como\(k \to \infty\).
Prueba
Estas propiedades son claras a partir de la forma funcional de\( r_k(p) \). Tenga en cuenta que\( r_k(p) = r_k(1 - p) \).
Para\( k \in \{2, 3, 4\} \),\(r_k\) cuenta con las siguientes propiedades:
- \( r_k \)aumenta y luego disminuye, con el máximo en\(p = \frac{1}{2}\).
- \( r_k \)es cóncavo hacia abajo
Prueba
Esto sigue calculando las primeras derivadas:\(r_2^\prime(p) = 2 (1 - 2 p)\),\(r_3^\prime(p) = 3 (1 - 2 p)\),\(r_4^\prime(p) = 4 (1 - 2 p)^3\), y las segundas derivadas:\( r_2^{\prime\prime}(p) = -4 \),\( r_3^{\prime\prime}(p) = - 6 \),\( r_4^{\prime\prime}(p) = -24 (1 - 2 p)^2 \).
Para\( k \in \{5, 6, \ldots\} \),\(r_k\) cuenta con las siguientes propiedades:
- El máximo ocurre en dos puntos de la forma\(p_k\) y\(1 - p_k\) dónde\( p_k \in \left(0, \frac{1}{2}\right) \) y\(p_k \to 0\) como\(k \to \infty\).
- El valor máximo\(r_k(p_k) \to 1/e \approx 0.3679\) como\(k \to \infty\).
- La gráfica tiene un mínimo local en\(p = \frac{1}{2}\).
Croquis de prueba
Tenga en cuenta que\(r_k(p) = s_k(p) + s_k(1 - p)\) donde\(s_k(t) = k t^{k-1}(1 - t)\) para\(t \in [0, 1]\). También,\(p \mapsto s_k(p)\) es el término dominante cuando\(p \gt \frac{1}{2}\) mientras\(p \mapsto s_k(1 - p)\) es el término dominante cuando\(p \lt \frac{1}{2}\). Un simple análisis de la derivada muestra que\(s_k\) aumenta y luego disminuye, alcanzando su máximo en\((k - 1) / k\). Además, el valor máximo es\(s_k\left[(k - 1) / k\right] = (1 - 1 / k)^{k-1} \to e^{-1}\) como\(k \to \infty\). También,\( s_k \) es cóncava hacia arriba y luego hacia abajo, ingenio punto de inflexión en\( (k - 2) / k \).
Supongamos\(p \in (0, 1)\), y vamos a\(N_k\) denotar el número de rondas hasta que se elimine a un hombre impar, comenzando por\(k\) jugadores. Después\(N_k\) tiene la distribución geométrica\(\N_+\) encendida con parámetro\(r_k(p)\). La media y varianza son
- \(\mu_k(p) = 1 \big/ r_k(p)\)
- \(\sigma_k^2(p) = \left[1 - r_k(p)\right] \big/ r_k^2(p)\)
Como cabría esperar,\(\mu_k(p) \to \infty\) y en\(\sigma_k^2(p) \to \infty\)\(k \to \infty\) cuanto a fijo\(p \in (0, 1)\). Por otro lado, a partir del resultado anterior,\(\mu_k(p_k) \to e\) y\(\sigma_k^2(p_k) \to e^2 - e\) como\(k \to \infty\).
Supongamos que empezamos con\(k \in \{2, 3, \ldots\}\) jugadores y\(p \in (0, 1)\). El número de rondas hasta que queda un solo jugador es\(M_k = \sum_{j = 2}^k N_j\) donde\((N_2, N_3, \ldots, N_k)\) son independientes y\(N_j\) tiene la distribución geométrica encendida\(\N_+\) con parámetro\(r_j(p)\). La media y varianza son
- \(\E(M_k) = \sum_{j=2}^k 1 \big/ r_j(p)\)
- \(\var(M_k) = \sum_{j=2}^k \left[1 - r_j(p)\right] \big/ r_j^2(p)\)
Prueba
La forma de\(M_k\) sigue del resultado anterior:\(N_k\) es el número de rondas hasta que el primer jugador sea eliminado. Entonces el juego continúa de manera independiente con\(k - 1\) los jugadores, así\(N_{k-1}\) es el número de rondas adicionales hasta que se elimine al segundo jugador, y así sucesivamente. Las partes (a) y (b) siguen del resultado anterior y las propiedades estándar del valor esperado y la varianza.
Empezando por\(k\) jugadores y probabilidad de cabezas\(p \in (0, 1)\), el número total de tiradas de monedas es\(T_k = \sum_{j=2}^k j N_j\). La media y varianza son
- \(\E(T_k) = \sum_{j=2}^k j \big/ r_j(p)\)
- \(\var(T_k) = \sum_{j=2}^k j^2 \left[1 - r_j(p)\right] \big/ r_j^2(p)\)
Prueba
Como antes, la forma de\(M_k\) sigue del resultado anterior:\(N_k\) es el número de rondas hasta que el primer jugador es eliminado, y cada una de estas rondas tiene\(k\) tiradas. Entonces el juego continúa de manera independiente con\(k - 1\) los jugadores, así\(N_{k-1}\) es el número de rondas adicionales hasta que el segundo jugador sea eliminado con cada ronda teniendo\(k - 1\) tiradas, y así sucesivamente. Las partes (a) y (b) también se desprenden del resultado anterior y las propiedades estándar del valor esperado y la varianza.
Número de ensayos antes de un patrón
Consideremos nuevamente una secuencia de ensayos de Bernoulli\( \bs X = (X_1, X_2, \ldots) \) con parámetro de éxito\( p \in (0, 1) \). Recordemos que el número de ensayos\( M \) antes de que ocurra el primer éxito (resultado 1) tiene la distribución geométrica on\( \N \) con parámetro\( p \). Una generalización natural es la variable aleatoria que da el número de ensayos antes de que ocurra por primera vez una secuencia finita específica de resultados. (Tal secuencia a veces se refiere como una palabra del alfabeto\( \{0, 1\} \) o simplemente una cadena de bits). En general, encontrar la distribución de esta variable es un problema difícil, con la dificultad dependiendo mucho de la naturaleza de la palabra. El problema de encontrar solo el número esperado de ensayos antes de que ocurra una palabra puede resolverse utilizando poderosas herramientas de la teoría de los procesos de renovación y de la teoría de las martingalgas.
Para configurar la notación, vamos\( \bs x \) denotar una cadena de bits finitos y dejar\( M_{\bs x} \) denotar el número de pruebas antes de que\( \bs x \) ocurra por primera vez. Por último, vamos\( q = 1 - p \). Tenga en cuenta que\( M_{\bs x} \) toma valores en\( \N \). En los siguientes ejercicios, consideraremos\( \bs x = 10 \), un éxito seguido de un fracaso. Como siempre, intenta derivar los resultados tú mismo antes de mirar las pruebas.
La función de densidad de probabilidad\( f_{10} \) de\( M_{10} \) se da de la siguiente manera:
- Si\( p \ne \frac{1}{2} \) entonces\[ f_{10}(n) = p q \frac{p^{n+1} - q^{n+1}}{p - q}, \quad n \in \N \]
- Si\(p = \frac{1}{2}\) entonces\( f_{10}(n) = (n + 1) \left(\frac{1}{2}\right)^{n+2} \) por\( n \in \N \).
Prueba
Para\( n \in \N \), el evento solo\(\{M_{10} = n\}\) puede ocurrir si hay una cadena inicial de 0s de longitud\( k \in \{0, 1, \ldots, n\} \) seguida de una cadena de 1s de longitud\( n - k \) y luego 1 en juicio\( n + 1 \) y 0 en juicio\( n + 2 \). De ahí que\[ f_{10}(n) = \P(M_{10} = n) = \sum_{k=0}^n q^k p^{n - k} p q, \quad n \in \N \] el resultado declarado se deduce luego de los resultados estándar sobre series geométricas.
Es interesante notar que\( f \) es simétrico en\( p \) y\( q \), es decir, simétrico sobre\( p = \frac{1}{2} \). De ello se deduce que la función de distribución, la función generadora de probabilidad, el valor esperado y la varianza, que consideramos a continuación, son también simétricas\( p = \frac{1}{2} \). También es interesante señalar eso\( f_{10}(0) = f_{10}(1) = p q \), y este es el mayor valor. Entonces independientemente de\( p \in (0, 1) \) la distribución es bimodal con los modos 0 y 1.
La función\( F_{10} \) de distribución de\( M_{10} \) se da de la siguiente manera:
- Si\( p \ne \frac{1}{2} \) entonces\[ F_{10}(n) = 1 - \frac{p^{n+3} - q^{n+3}}{p - q}, \quad n \in \N \]
- Si\( p = \frac{1}{2} \) entonces\( F_{10} = 1 - (n + 3) \left(\frac{1}{2}\right)^{n+2} \) por\( n \in \N \).
Prueba
Por definición,\(F_{10}(n) = \sum_{k=0}^n f_{10}(k)\) para\( n \in \N \). El resultado declarado se desprende entonces del teorema anterior, los resultados estándar sobre series geométricas y algo de álgebra.
La función de generación de probabilidad\( P_{10} \) de\( M_{10} \) se da de la siguiente manera:
- Si\( p \ne \frac{1}{2} \) entonces\[ P_{10}(t) = \frac{p q}{p - q} \left(\frac{p}{1 - t p} - \frac{q}{1 - t q}\right), \quad |t| \lt \min \{1 / p, 1 / q\} \]
- Si\( p = \frac{1}{2} \) entonces\(P_{10}(t) = 1 / (t - 2)^2\) por\( |t| \lt 2 \)
Prueba
Por definición,\[ P_{10}(t) = \E\left(t^{M_{10}}\right) = \sum_{n=0}^\infty f_{10}(n) t^n \] para todos\( t \in \R \) para los que la serie converge absolutamente. El resultado declarado se desprende entonces del teorema anterior, y una vez más, los resultados estándar sobre series geométricas.
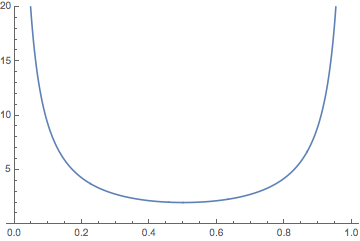
La media de\( M_{10} \) se da de la siguiente manera:
- Si\( p \ne \frac{1}{2} \) entonces\[ \E(M_{10}) = \frac{p^4 - q^4}{p q (p - q)} \]
- Si\( p = \frac{1}{2} \) entonces\( \E(M_{10}) = 2 \).
Prueba
Recordemos que\( \E(M_{10}) = P^\prime_{10}(1) \) así el resultado declarado se desprende del cálculo, utilizando el teorema anterior sobre la función generadora de probabilidad. La media también se puede calcular a partir de la definición\( \E(M_{10}) = \sum_{n=0}^\infty n f_{10}(n) \) utilizando resultados estándar de series geométricas, pero este método es más tedioso.
La gráfica de\( \E(M_{10}) \) como una función de\( p \in (0, 1) \) se da a continuación. No es de extrañar que\( \E(M_{10}) \to \infty \) como\( p \downarrow 0 \) y como\( p \uparrow 1 \), y que el valor mínimo ocurra cuando\( p = \frac{1}{2} \).
La varianza de\( M_{10} \) se da de la siguiente manera:
- Si\( p \ne \frac{1}{2} \) entonces\[ \var(M_{10}) = \frac{2}{p^2 q^2} \left(\frac{p^6 - q^6}{p - q}\right) + \frac{1}{p q} \left(\frac{p^4 - q^4}{p - q}\right) - \frac{1}{p^2 q^2}\left(\frac{p^4 - q^4}{p - q}\right)^2 \]
- Si\( p = \frac{1}{2} \) entonces\( \var(M_{10}) = 4 \).
Prueba
Recordemos que\( P^{\prime \prime}_{10}(1) = \E[M_{10}(M_{10} - 1)] \), el segundo momento factorial, y así\[ \var(M_{10}) = P^{\prime \prime}_{10}(1) + P^\prime_{10}(1) - [P^\prime_{10}(1)]^2 \] El resultado declarado se desprende entonces del cálculo y del teorema anterior dando la función generadora de probabilidad.


