12.9: El problema del secretario
- Page ID
- 151932
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección estudiaremos un problema agradable conocido de diversas maneras como el problema de la secretaria o el problema del matrimonio. Es sencillo de afirmar y no difícil de resolver, pero la solución es interesante y un poco sorprendente. Además, el problema sirve como una agradable introducción al área general de la toma de decisiones estadísticas.
Declaración del problema
Como siempre, debemos comenzar con una clara declaración del problema.
Tenemos\(n\) candidatos (tal vez aspirantes a un trabajo o posibles parejas matrimoniales). Los supuestos son
- Los candidatos están totalmente ordenados de mejor a peor sin vínculos.
- Los candidatos llegan secuencialmente en orden aleatorio.
- Sólo podemos determinar los rangos relativos de los candidatos a medida que llegan. No podemos observar las filas absolutas.
- Nuestro objetivo es elegir al mejor candidato; nadie menos va a hacer.
- Una vez rechazada a una candidata, se va para siempre y no puede ser recordada.
- Se conoce el número\(n\) de candidatos.
Los supuestos, por supuesto, no son del todo razonables en aplicaciones reales. El último supuesto, por ejemplo, que\(n\) se conoce, es más apropiado para la interpretación del secretario que para la interpretación del matrimonio.
¿Cuál es una estrategia óptima? ¿Cuál es la probabilidad de éxito con esta estrategia? ¿Qué pasa con la estrategia y la probabilidad de éxito a medida que\(n\) aumenta? En particular, cuando\(n\) es grande, ¿hay alguna esperanza razonable de encontrar al mejor candidato?
Estrategias
Juega el juego de secretaria varias veces con\(n = 10\) los candidatos. Ve si puedes encontrar una buena estrategia solo por prueba y error.
Después de jugar algunas veces el juego de secretaria, debe quedar claro que el único tipo de estrategia razonable es dejar pasar un cierto número\(k - 1\) de candidatos, para luego seleccionar al primer candidato vemos quién es mejor que todos los candidatos anteriores (si existe). Si ella no existe (es decir, si no aparece ninguna candidata mejor que todos los candidatos anteriores), estaremos de acuerdo en aceptar al último candidato, aunque esto signifique fracaso. El parámetro\(k\) debe estar entre 1 y\(n\); si\(k = 1\), seleccionamos el primer candidato; si\(k = n\), seleccionamos el último candidato; para cualquier otro valor de\(k\), el candidato seleccionado es aleatorio, distribuido en\(\{k, k + 1, \ldots, n\}\). Nos referiremos a esto dejar\(k - 1\) ir por
estrategia como estrategia\(k\).
Por lo tanto, necesitamos calcular la probabilidad de éxito\(p_n(k)\) usando estrategia\(k\) con\(n\) candidatos. Entonces podemos maximizar la probabilidad de\(k\) encontrar la estrategia óptima, y luego tomar el límite\(n\) para estudiar el comportamiento asintótico.
Análisis
Primero, hagamos algunos cálculos básicos.
Para el caso\(n = 3\), enumere las 6 permutaciones de\(\{1, 2, 3\}\) y verifique las probabilidades en la siguiente tabla. Tenga en cuenta que\(k = 2\) es óptimo.
| \(k\) | 1 | 2 | 3 |
|---|---|---|---|
| \(p_3(k)\) | \(\frac{2}{6}\) | \(\frac{3}{6}\) | \(\frac{2}{6}\) |
Contestar
La siguiente tabla da las\( 3! = 6 \) permutaciones de los candidatos\( (1, 2, 3) \), y el candidato seleccionado por cada estrategia. La última fila da el número total de éxitos para cada estrategia.
| Permutación | \(k = 1\) | \(k = 2\) | \(k = 3\) |
|---|---|---|---|
| \((1, 2, 3)\) | 1 | 3 | 3 |
| \((1, 3, 2)\) | 1 | 2 | 2 |
| \((2, 1, 3)\) | 2 | 1 | 3 |
| \((2, 3, 1)\) | 2 | 1 | 1 |
| \((3, 1, 2)\) | 3 | 1 | 2 |
| \((3, 2, 1)\) | 3 | 2 | 1 |
| Total | 2 | 3 | 2 |
En el experimento secretario, establecer el número de candidatos en\(n = 3\). Ejecuta el experimento 1000 veces con cada estrategia\( k \in \{1, 2, 3\} \)
Para el caso\(n = 4\), enumere las 24 permutaciones de\(\{1, 2, 3, 4\}\) y verifique las probabilidades en la siguiente tabla. Tenga en cuenta que\(k = 2\) es óptimo. La última fila da el número total de éxitos para cada estrategia.
| \(k\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(p_4(k)\) | \(\frac{6}{24}\) | \(\frac{11}{24}\) | \(\frac{10}{24}\) | \(\frac{6}{24}\) |
Contestar
La siguiente tabla da las\(4! = 24\) permutaciones de los candidatos\((1, 2, 3, 4)\), y el candidato seleccionado por cada estrategia.
| Permutación | \(k = 1\) | \(k = 2\) | \(k = 3\) | \(k = 4\) |
|---|---|---|---|---|
| \((1, 2, 3, 4)\) | 1 | 4 | 4 | 4 |
| \((1, 2, 4, 3)\) | 1 | 3 | 3 | 3 |
| \((1, 3, 2, 4)\) | 1 | 4 | 4 | 4 |
| \((1, 3, 4, 2)\) | 1 | 3 | 2 | 2 |
| \((1, 4, 2, 3)\) | 1 | 3 | 3 | 3 |
| \((1, 4, 3, 2)\) | 1 | 2 | 2 | 2 |
| \((2, 1, 3, 4)\) | 2 | 1 | 4 | 4 |
| \((2, 1, 4, 3)\) | 2 | 1 | 3 | 3 |
| \((2, 3, 1, 4)\) | 2 | 1 | 1 | 4 |
| \((2, 3, 4, 1)\) | 2 | 1 | 1 | 1 |
| \((2, 4, 1, 3)\) | 2 | 1 | 1 | 3 |
| \((2, 4, 3, 1)\) | 2 | 1 | 1 | 1 |
| \((3, 1, 2, 4)\) | 3 | 1 | 4 | 4 |
| \((3, 1, 4, 2)\) | 3 | 1 | 2 | 2 |
| \((3, 2, 1, 4)\) | 3 | 2 | 1 | 4 |
| \((3, 2, 4, 1)\) | 3 | 2 | 1 | 1 |
| \((3, 4, 1, 2)\) | 3 | 1 | 1 | 2 |
| \((3, 4, 2, 1)\) | 3 | 2 | 2 | 1 |
| \((4, 1, 2, 3)\) | 4 | 1 | 3 | 3 |
| \((4, 1, 3, 2)\) | 4 | 1 | 2 | 2 |
| \((4, 2, 1, 3)\) | 4 | 2 | 1 | 3 |
| \((4, 2, 3, 1)\) | 4 | 2 | 1 | 1 |
| \((4, 3, 1, 2)\) | 4 | 3 | 1 | 2 |
| \((4, 3, 2, 1)\) | 4 | 3 | 2 | 1 |
| Total | 6 | 11 | 10 | 6 |
En el experimento secretario, establecer el número de candidatos en\(n = 4\). Ejecuta el experimento 1000 veces con cada estrategia\( k \in \{1, 2, 3, 4\} \)
Para el caso\(n = 5\), enumere las 120 permutaciones de\(\{1, 2, 3, 4, 5\}\) y verifique las probabilidades en la siguiente tabla. Tenga en cuenta que\(k = 3\) es óptimo.
| \(k\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(p_5(k)\) | \(\frac{24}{120}\) | \(\frac{50}{120}\) | \(\frac{52}{120}\) | \(\frac{42}{120}\) | \(\frac{24}{120}\) |
En el experimento secretario, establecer el número de candidatos en\(n = 5\). Ejecuta el experimento 1000 veces con cada estrategia\( k \in \{1, 2, 3, 4, 5\} \)
Bueno, claramente no queremos seguir haciendo esto. Veamos si podemos encontrar un análisis general. Con\(n\) los candidatos, vamos a\(X_n\) denotar el número (orden de llegada) del mejor candidato, y dejar\(S_{n,k}\) denotar el evento de éxito para la estrategia\(k\) (seleccionamos al mejor candidato).
\(X_n\)se distribuye uniformemente en\(\{1, 2, \ldots, n\}\).
Prueba
Esto sigue ya que los candidatos llegan en orden aleatorio.
A continuación calcularemos la probabilidad condicional de éxito dado el orden de llegada del mejor candidato.
Para\( n \in \N_+ \) y\( k \in \{2, 3, \ldots, n\} \),\[ \P(S_{n,k} \mid X_n = j) = \begin{cases} 0, & j \in \{1, 2, \ldots, k-1\} \\ \frac{k-1}{j-1}, & j \in \{k, k + 1, \ldots, n\} \end{cases} \]
Prueba
Para el primer caso, tenga en cuenta que si el número de llegada del mejor candidato es\(j \lt k\), entonces la estrategia seguramente\(k\) fallará. Para los segundos casos, tenga en cuenta que si el orden de llegada del mejor candidato es\(j \ge k\), entonces la estrategia\(k\) tendrá éxito si y solo si uno de los primeros\(k - 1\) candidatos (los que se rechazan automáticamente) es el mejor entre los primeros\(j - 1\)
Los dos casos se ilustran a continuación. El punto grande indica el mejor candidato. Los puntos rojos indican candidatos que son rechazados de la mano, mientras que los puntos azules indican candidatos que son considerados.
Figura\(\PageIndex{1}\): El caso cuando\( X_n = j \lt k \)
Figura\(\PageIndex{2}\): El caso cuando\( X_n = j \ge k \)
Ahora podemos calcular la probabilidad de éxito con la estrategia\(k\).
Para\( n \in \N_+ \)\[ p_n(k) = \P(S_{n,k}) = \begin{cases} \frac{1}{n}, & k = 1 \\ \frac{k - 1}{n} \sum_{j=k}^n \frac{1}{j - 1}, & k \in \{2, 3, \ldots, n\} \end{cases} \]
Prueba
Cuando simplemente\( k = 1 \) seleccionamos al primer candidato. Este candidato será el mejor con probabilidad\( 1 / n \). El resultado para\( k \in \{2, 3, \ldots, n\} \) se desprende de los dos resultados anteriores, condicionando a\(X_n\):\[ \P(S_{n,k}) = \sum_{j=1}^n \P(X_n = j) \P(S_{n,k} \mid X_n = j) = \sum_{j=k}^n \frac{1}{n} \frac{k - 1}{j - 1} \]
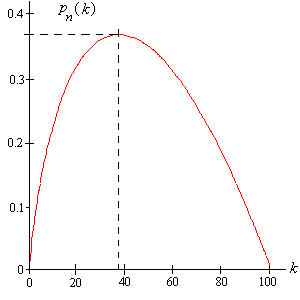
Los valores de la función\(p_n\) pueden ser calculados a mano para pequeños\(n\) y por un sistema de álgebra computacional para moderado\(n\). A continuación\(p_{100}\) se muestra la gráfica de. Observe la forma cóncava hacia abajo de la gráfica y el valor óptimo de\(k\), que resulta ser 38. La probabilidad óptima es de aproximadamente 0.37104.
La estrategia óptima\(k_n\) que maximiza\(k \mapsto p_n(k)\), la relación\(k_n / n\) y la probabilidad óptima\(p_n(k_n)\) de encontrar al mejor candidato, como funciones de\(n \in \{3, 4, \dots, 20\}\) se dan en la siguiente tabla:
| Candidatos\(n\) | Estrategia óptima\(k_n\) | Ratio\(k_n / n\) | Probabilidad óptima\(p_n(k_n)\) |
|---|---|---|---|
| \ (n\) ">3 | \ (k_n\) ">2 | \ (k_n/n\) ">0.6667 | \ (p_n (k_n)\) ">0.5000 |
| \ (n\) ">4 | \ (k_n\) ">2 | \ (k_n/n\) ">0.5000 | \ (p_n (k_n)\) ">0.4583 |
| \ (n\) ">5 | \ (k_n\) ">3 | \ (k_n/n\) ">0.6000 | \ (p_n (k_n)\) ">0.4333 |
| \ (n\) ">6 | \ (k_n\) ">3 | \ (k_n/n\) ">0.5000 | \ (p_n (k_n)\) ">0.4278 |
| \ (n\) ">7 | \ (k_n\) ">3 | \ (k_n/n\) ">0.4286 | \ (p_n (k_n)\) ">0.4143 |
| \ (n\) ">8 | \ (k_n\) ">4 | \ (k_n/n\) ">0.5000 | \ (p_n (k_n)\) ">0.4098 |
| \ (n\) ">9 | \ (k_n\) ">4 | \ (k_n/n\) ">0.4444 | \ (p_n (k_n)\) ">0.4060 |
| \ (n\) ">10 | \ (k_n\) ">4 | \ (k_n/n\) ">0.4000 | \ (p_n (k_n)\) ">0.3987 |
| \ (n\) ">11 | \ (k_n\) ">5 | \ (k_n/n\) ">0.4545 | \ (p_n (k_n)\) ">0.3984 |
| \ (n\) ">12 | \ (k_n\) ">5 | \ (k_n/n\) ">0.4167 | \ (p_n (k_n)\) ">0.3955 |
| \ (n\) ">13 | \ (k_n\) ">6 | \ (k_n/n\) ">0.4615 | \ (p_n (k_n)\) ">0.3923 |
| \ (n\) ">14 | \ (k_n\) ">6 | \ (k_n/n\) ">0.4286 | \ (p_n (k_n)\) ">0.3917 |
| \ (n\) ">15 | \ (k_n\) ">6 | \ (k_n/n\) ">0.4000 | \ (p_n (k_n)\) ">0.3894 |
| \ (n\) ">16 | \ (k_n\) ">7 | \ (k_n/n\) ">0.4375 | \ (p_n (k_n)\) ">0.3881 |
| \ (n\) ">17 | \ (k_n\) ">7 | \ (k_n/n\) ">0.4118 | \ (p_n (k_n)\) ">0.3873 |
| \ (n\) ">18 | \ (k_n\) ">7 | \ (k_n/n\) ">0.3889 | \ (p_n (k_n)\) ">0.3854 |
| \ (n\) ">19 | \ (k_n\) ">8 | \ (k_n/n\) ">0.4211 | \ (p_n (k_n)\) ">0.3850 |
| \ (n\) ">20 | \ (k_n\) ">8 | \ (k_n/n\) ">0.4000 | \ (p_n (k_n)\) ">0.3842 |
Al parecer, como cabría esperar, la estrategia óptima\(k_n\) aumenta y la probabilidad óptima\(p_n(k_n)\) disminuye como\(n \to \infty\). Por otro lado, es alentador, y un poco sorprendente, que la probabilidad óptima no parezca estar disminuyendo a 0. Quizás esté menos claro qué está pasando con la proporción. Las pantallas gráficas de parte de la información de la tabla pueden ayudar a:
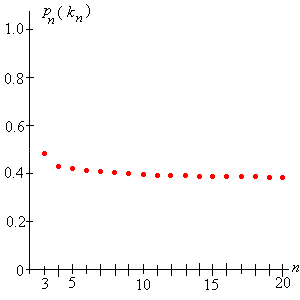
Figura\(\PageIndex{4}\): La probabilidad óptima\( p_n(k_n) \)
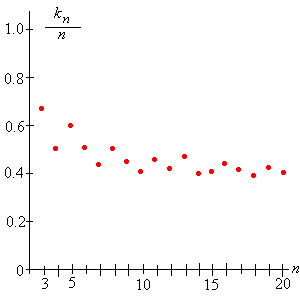
Figura\(\PageIndex{5}\): La relación óptima\( k_n / n \)
¿Podría ser que tanto la relación\(k_n / n\) como la probabilidad\(p_n(k_n)\) estén convergiendo, y además, estén convergiendo al mismo número? Primero intentemos establecer rigurosamente algunas de las tendencias observadas en la tabla.
La probabilidad de éxito\(p_n\) satisface\[ p_n(k - 1) \lt p_n(k) \text{ if and only if } \sum_{j=k}^n \frac{1}{j-1} \gt 1 \]
De ello se deduce que para cada uno\(n \in \N_+\), la función\(p_n\) al principio aumenta y luego disminuye. El valor máximo de\(p_n\) ocurre en el mayor\(k\) con\(\sum_{j=k}^n \frac{1}{j - 1} \gt 1\). Esta es la estrategia óptima con\(n\) los candidatos, que hemos denotado por\(k_n\).
A\(n\) medida que\(k_n\) aumenta, aumenta y\(p_n(k_n)\) disminuye la probabilidad óptima.
Análisis asintótico
Estamos naturalmente interesados en el comportamiento asintótico de la función\(p_n\), y la estrategia óptima como\(n \to \infty\). La clave es reconocer\(p_n\) como una suma de Riemann para una integral simple. (Las sumas de Riemann, por supuesto, llevan el nombre de Georg Riemann.)
Si\(k(n)\) depende de\(n\) y\(k(n) / n \to x \in (0, 1)\) como\(n \to \infty\) entonces\(p_n[k(n)] \to -x \ln x\) como\(n \to \infty\).
Prueba
Primero tenga en cuenta que\[ p_n(k) = \frac{k-1}{n} \sum_{j=k}^n \frac{1}{n} \frac{n}{j-1} \] Reconocemos la suma anterior como la suma de Riemann izquierda para la función\(f(t) = \frac{1}{t}\) correspondiente a la partición del intervalo\(\left[\frac{k-1}{n}, 1\right]\) en\((n - k) + 1\) subintervalos de longitud\(\frac{1}{n}\) cada uno:\(\left(\frac{k-1}{n}, \frac{k}{n}, \ldots, \frac{n-1}{n}, 1\right)\). De ello se deduce que\[ p_n[k(n)] \to x \int_x^1 \frac{1}{t} dt = -x \ln x \text{ as } n \to \infty\]
La estrategia óptima\(k_n\) que maximiza\(k \mapsto p_n(k)\), la relación\(k_n / n\) y la probabilidad óptima\(p_n(k_n)\) de encontrar al mejor candidato, como funciones de\(n \in \{10, 20, \dots, 100\}\) se dan en la siguiente tabla:
| Candidatos\(n\) | Estrategia óptima\(k_n\) | Ratio\(k_n / n\) | Probabilidad óptima\(p_n(k_n)\) |
|---|---|---|---|
| \ (n\) ">10 | \ (k_n\) ">4 | \ (k_n/n\) ">0.4000 | \ (p_n (k_n)\) ">0.3987 |
| \ (n\) ">20 | \ (k_n\) ">8 | \ (k_n/n\) ">0.4000 | \ (p_n (k_n)\) ">0.3842 |
| \ (n\) ">30 | \ (k_n\) ">12 | \ (k_n/n\) ">0.4000 | \ (p_n (k_n)\) ">0.3786 |
| \ (n\) ">40 | \ (k_n\) ">16 | \ (k_n/n\) ">0.4000 | \ (p_n (k_n)\) ">0.3757 |
| \ (n\) ">50 | \ (k_n\) ">19 | \ (k_n/n\) ">0.3800 | \ (p_n (k_n)\) ">0.3743 |
| \ (n\) ">60 | \ (k_n\) ">23 | \ (k_n/n\) ">0.3833 | \ (p_n (k_n)\) ">0.3732 |
| \ (n\) ">70 | \ (k_n\) ">27 | \ (k_n/n\) ">0.3857 | \ (p_n (k_n)\) ">0.3724 |
| \ (n\) ">80 | \ (k_n\) ">30 | \ (k_n/n\) ">0.3750 | \ (p_n (k_n)\) ">0.3719 |
| \ (n\) ">90 | \ (k_n\) ">34 | \ (k_n/n\) ">0.3778 | \ (p_n (k_n)\) ">0.3714 |
| \ (n\) ">100 | \ (k_n\) ">38 | \ (k_n/n\) ">0.3800 | \ (p_n (k_n)\) ">0.3710 |
La gráfica siguiente muestra las probabilidades verdaderas\(p_n(k)\) y los valores\(-\frac{k}{n} \, \ln\left(\frac{k}{n}\right)\) limitantes en función de\(k\) con\(n = 100\).
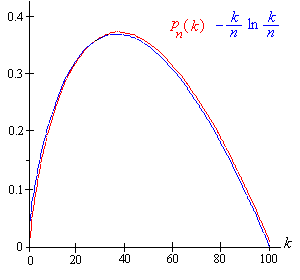
Para la estrategia óptima\(k_n\), existe\(x_0 \in (0, 1)\) tal que\(k_n / n \to x_0\) como\(n \to \infty\). Así,\(x_0 \in (0, 1)\) es la proporción limitante de los candidatos que rechazamos de las manos. Además,\(x_0\) maximiza\(x \mapsto -x \ln x\) en\((0, 1)\).
El valor máximo de\(-x \ln x\) ocurre en\(x_0 = 1 / e\) y el valor máximo también es\(1 / e\).
Prueba
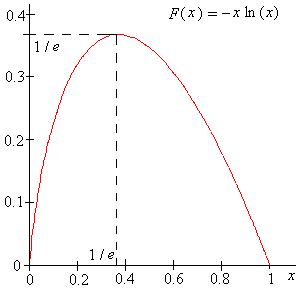
Así, el número mágico\(1 / e \approx 0.3679\) ocurre dos veces en el problema. Para grandes\(n\):
- Nuestra estrategia óptima aproximada es rechazar de la mano al primer 37% de los candidatos y luego seleccionar al primer candidato (si aparece) que sea mejor que todos los candidatos anteriores.
- Nuestra probabilidad de encontrar al mejor candidato es de aproximadamente 0.37.
El artículo ¿Quién resolvió el problema del secretario?
de Tom Ferguson (1989) tiene una interesante discusión histórica sobre el problema, incluida la especulación de que Johannes Kepler pudo haber utilizado la estrategia óptima para elegir a su segunda esposa. El artículo también discute muchas generalizaciones interesantes del problema. Una versión diferente del problema de la secretaria, en la que a los candidatos se les asigna una puntuación en\([0, 1]\), en lugar de un rango relativo, se discute en la sección de Tiempos de parada en el capítulo sobre Martingales