16.4: Tranquiencia y Recurrencia para Cadenas Discretas de Tiempo
- Page ID
- 151957
El estudio de las cadenas de Markov de tiempo discreto, particularmente el comportamiento limitante, depende críticamente de los tiempos aleatorios entre visitas a un estado determinado. La naturaleza de estos tiempos aleatorios conduce a una dicotomía fundamental de los estados.
Teoría Básica
Como es habitual, nuestro punto de partida es un espacio de probabilidad\( (\Omega, \mathscr{F}, \P) \), por lo que\( \Omega \) es el espacio\( \mathscr{F} \) muestral, el\( \sigma \) álgebra de eventos y\( \P \) la medida de probabilidad en\( (\Omega, \mathscr{F}) \). Supongamos ahora que\( \bs{X} = (X_0, X_1, X_2, \ldots) \) es una cadena de Markov de tiempo discreto (homogénea) con espacio de estado (contable)\( S \) y matriz de probabilidad de transición\( P \). Entonces por definición,\[ P(x, y) = \P(X_{n+1} = y \mid X_n = x) \] para\( x, \, y \in S \) y\( n \in \N \). Let\( \mathscr{F}_n = \sigma\{X_0, X_1, \ldots, X_n\} \), la\( \sigma \) -álgebra de eventos definidos por la cadena hasta el tiempo\( n \in \N \), así que esa\( \mathfrak{F} = (\mathscr{F}_0, \mathscr{F}_1, \ldots) \) es la filtración natural asociada con\( \bs{X} \).
Tiempos y Probabilidades de Golpeado
Dejar\( A \) ser un subconjunto no vacío de\( S \). Recordemos que el tiempo de bateo a\( A \) es la variable aleatoria que da el primer tiempo positivo en el que se encuentra la cadena\( A \):\[ \tau_A = \min\{n \in \N_+: X_n \in A\} \] Dado que la cadena nunca puede entrar\( A \), la variable aleatoria\( \tau_A \) toma valores\( \N_+ \cup \{\infty\} \) (recordemos nuestra convención de que el mínimo del conjunto vacío es\( \infty \)). Recordemos también que\( \tau_A \) es un tiempo de parada para\( \bs{X} \). Es decir,\( \{\tau_A = n\} \in \mathscr{F}_n \) para\( n \in \N_+ \). Intuitivamente, esto significa que podemos decir si\( \tau_A = n \) observando la cadena hasta el tiempo\( n \). Esto es claramente el caso, ya que explícitamente\[ \{\tau_A = n\} = \{X_1 \notin A, \ldots, X_{n-1} \notin A, X_n \in A\} \] Cuando\( A = \{x\} \) para\( x \in S \), vamos a simplificar la notación a\( \tau_x \). Esta variable aleatoria da el primer tiempo positivo que la cadena está en estado\( x \). Cuando la cadena ingresa\( A \) por primera vez a un conjunto de estados, la cadena debe visitar algún estado en\( A \) por primera vez, por lo que queda claro que\[ \tau_A = \min\{\tau_x: x \in A\}, \quad A \subseteq S \] Siguiente definimos dos funciones sobre las\( S \) que están relacionadas con los tiempos de bateo.
Para\( x \in S \),\( A \subseteq S \) (no vacío), y\( n \in \N_+ \) definir
- \( H_n(x, A) = \P(\tau_A = n \mid X_0 = x)\)
- \(H(x, A) = \P(\tau_A \lt \infty \mid X_0 = x) \)
Entonces\( H(x, A) = \sum_{n=1}^\infty H_n(x, A) \).
Obsérvese que\( n \mapsto H_n(x, A) \) es la función de densidad de probabilidad de\( \tau_A \)\( X_0 = x \), dada, excepto que la función de densidad puede ser defectuosa en el sentido de que la suma\( H(x, A) \) puede ser inferior a 1, en cuyo caso claro,\( 1 - H(x, A) = \P(\tau_A = \infty \mid X_0 = x) \). Nuevamente, cuando\( A = \{y\} \), vamos a simplificar la notación a\( H_n(x, y) \) y\( H(x, y) \), respectivamente. En particular,\( H(x, x) \) es la probabilidad, a partir de\( x \), a que la cadena finalmente vuelva a\( x \). Si\( x \ne y \),\( H(x, y) \) es la probabilidad, a partir de\( x \), que la cadena finalmente alcanza\( y \). Solo saber cuándo\( H(x, y) \) es 0, positivo, y 1 resultará ser de considerable importancia en la estructura general y el comportamiento limitante de la cadena. En función de\( S^2 \), nos referiremos\( H \) como la matriz de golpeo de\( \bs{X} \). Tenga en cuenta sin embargo, que a diferencia de la matriz de transición\( P \), no tenemos la estructura de un kernel. Es decir, no\( A \mapsto H(x, A) \) es una medida, por lo que en particular, generalmente no es cierto que\( H(x, A) = \sum_{y \in A} H(x, y) \). Se aplican las mismas observaciones a\( H_n \) para\( n \in \N_+ \). Sin embargo, existen interesantes relaciones entre la matriz de transición y la matriz de golpeo.
\( H(x, y) \gt 0 \)si y sólo si\( P^n(x, y) \gt 0 \) para algunos\( n \in \N_+ \).
Prueba
Tenga en cuenta que\( \{X_n = y\} \subseteq \{\tau_y \lt \infty\} \) para todos\( n \in \N_+ \), y\( \{\tau_y \lt \infty\} = \{X_k = y \text{ for some } k \in \N_+\} \). De la creciente propiedad de probabilidad y la desigualdad de Boole se deduce que para cada uno\( n \in \N_+ \),\[ P^n(x, y) \le H(x, y) \le \sum_{k=1}^\infty P^k(x, y) \]
El siguiente resultado da una relación básica entre la secuencia de probabilidades de golpeo y la secuencia de probabilidades de transición.
Supongamos que\( (x, y) \in S^2 \). Entonces\[ P^n(x, y) = \sum_{k=1}^n H_k(x, y) P^{n-k}(y, y), \quad n \in \N_+ \]
Prueba
Este resultado se deduce del condicionamiento encendido\( \tau_y \). Comenzando en estado\( x \), la cadena está en estado en el\( y \) momento\( n \) si y sólo si la cadena golpea\( y \) por primera vez en algún tiempo anterior\( k \), y luego vuelve a\( y \) en los\( n - k \) pasos restantes. De manera más formal,\[ P^n(x, y) = \P(X_n = y \mid X_0 = x) = \sum_{k=0}^\infty \P(X_n = y \mid \tau_y = k, X_0 = x) \P(\tau_y = k \mid X_0 = x) \] Pero el evento\( \tau_y = k \) implica\( X_k = y \) y está en\( \mathscr{F}_k \). De ahí por la propiedad\[ \P(X_n = y \mid \tau_y = k, X_0 = x) = \P(X_n = y \mid X_k = y, \tau_y = k, X_0 = x) = \P(X_n = y \mid X_k = y) = P^k(x, y) \] de Markov, Claro, por definición,\( \P(\tau_y = k \mid X_0 = x) = H_k(x, y) \), por lo que el resultado sigue por sustitución.
Supongamos que\( x \in S \) y\( A \subseteq S \). Entonces
- \( H_{n+1}(x, A) = \sum_{y \notin A} P(x, y) H_n(y, A) \)para\( n \in \N_+ \)
- \( H(x, A) = P(x, A) + \sum_{y \notin A} P(x, y) H(y, A) \)
Prueba
Estos resultados siguen la forma de condicionamiento en\( X_1 \).
- Comenzando en estado\( x \), la cadena primero entra\( A \) en el tiempo\( n + 1 \) si y sólo si la cadena pasa a algún estado\( y \notin A \) en el tiempo 1, y luego del estado\( y \), primero entra\( A \) en\( n \) pasos. \[ H_{n+1}(x, A) = \P(\tau_A = n + 1 \mid X_0 = x) = \sum_{y \in S} \P(\tau_A = n + 1 \mid X_0 = x, X_1 = y) \P(X_1 = y \mid X_0 = x) \]Pero\( \P(\tau_A = n + 1 \mid X_0 = x, X_1 = y) = 0 \) para\( y \in A \). Por las propiedades homogéneas de Markov y tiempo,\( \P(\tau_A = n + 1 \mid X_0 = x, X_1 = y) = \P(\tau_A = n \mid X_0 = y) = H_n(x, A) \) para\( y \notin A \). Por supuesto\( \P(X_1 = y \mid X_0 = x) = P(x, y) \). Entonces el resultado sigue por sustitución.
- Comenzando en estado\( x \), la cadena finalmente entra\( A \) si y solo si entra\( A \) en el primer paso, o se mueve a algún otro estado\( y \notin A \) en el primer paso, y luego finalmente entra\( A \) desde\( y \). \[ H(x, A) = \P(\tau_A \lt \infty \mid X_0 = x) = \sum_{y \in S} \P(\tau_A \lt \infty \mid X_1 =y, X_0 = x) \P(X_1 = y \mid X_0 = x)\]Pero\( \P(\tau_A \lt \infty \mid X_1 = y, X_0 = x) = 1\) para\( y \in A \). Por las propiedades Markov y homogéneas,\(\P(\tau_A \lt \infty \mid X_1 = y, X_0 = x) = \P(\tau_A \lt \infty \mid X_0 = y) = H(y, A) \) para\( y \notin A \). Sustituyendo tenemos\[ H(x, A) = \sum_{y \in A} P(x, y) + \sum_{y \notin A} P(x, y) H(y, A) = P(x, A) + \sum_{y \notin A} P(x, y) H(y, A) \]
La siguiente definición es fundamental para el estudio de las cadenas de Markov.
Vamos\( x \in S \).
- Estado\( x \) es recurrente si\( H(x, x) = 1 \).
- Estado\( x \) es transitorio si\( H(x, x) \lt 1 \).
Así, comenzando en un estado recurrente, la cadena, con probabilidad 1, eventualmente regresará al estado. Como veremos, la cadena volverá al estado infinitamente a menudo con probabilidad 1, y los tiempos de las visitas formarán los tiempos de llegada de un proceso de renovación. Esta resultará ser la observación crítica en el estudio del comportamiento limitante de la cadena. Por el contrario, si la cadena comienza en un estado transitorio, entonces hay una probabilidad positiva de que la cadena nunca regrese al estado.
Conteo de variables y potenciales
Nuevamente, supongamos que\( A \) es un conjunto no vacío de estados. Un complemento natural del tiempo de bateo a\( A \) es la variable de conteo que da el número de visitas a\( A \) (en momentos positivos). Así, vamos\[ N_A = \sum_{n=1}^\infty \bs{1}(X_n \in A) \] Nota que\( N_A \) toma valor en\( \N \cup \{\infty\} \). En su mayoría nos interesará el caso especial\( A = \{x\} \) para\( x \in S \), y en este caso, simplificaremos la notación a\( N_x \).
Dejar\( G(x, A) = \E(N_A \mid X_0 = x) \) para\( x \in S \) y\( A \subseteq S \). Entonces\( G \) es un núcleo encendido\( S \) y\[ G(x, A) = \sum_{n=1}^\infty P^n(x, A) \]
Prueba
Tenga en cuenta que\[ G(x, A) = \E \left(\sum_{n=1}^\infty \bs{1}(X_n \in A) \biggm| X_0 = x\right) = \sum_{n=1}^\infty \P(X_n \in A \mid X_0 = x) = \sum_{n=1}^\infty P^n(x, A) \] El intercambio de suma y valor esperado se justifica ya que los términos son no negativos. Para fijo\( x \in S \),\( A \mapsto G(x, A) \) es una medida positiva en\( S \) ya que\( A \mapsto P^n(x, A) \) es una medida de probabilidad en\( S \) para cada uno\( n \in \N_+ \). Tenga en cuenta también que\( A \mapsto N_A \) es una medida aleatoria, contando\( S \) y por lo tanto\( A \mapsto G(x, A) \) es una medida positiva (determinista) sobre\( S \).
Así\( G(x, A) \) es el número esperado de visitas\( A \) a momentos positivos. Como es habitual, cuando\( A = \{y\} \) para\( y \in S \) simplificamos la notación a\( G(x, y) \), y luego más generalmente tenemos\( G(x, A) = \sum_{y \in A} G(x, y) \) para\( A \subseteq S \). Entonces, como una matriz en\( S \),\( G = \sum_{n=1}^\infty P^n \). La matriz\( G \) está estrechamente relacionada con la matriz potencial\( R \) de\( \bs{X} \), dada por\( R = \sum_{n=0}^\infty P^n \). Entonces\( R = I + G \), y\( R(x, y) \) da el número esperado de visitas a\( y \in S \) en todo momento (no sólo momentos positivos), a partir de\( x \in S \). La matriz\( G \) es más útil para nuestros propósitos en esta sección.
La distribución de\( N_y \) tiene una representación simple en cuanto a las probabilidades de golpeo. Tenga en cuenta que debido a la propiedad Markov y la propiedad homogénea del tiempo, cada vez que la cadena alcanza estado\( y \), el comportamiento futuro es independiente del pasado y es estocásticamente el mismo que la cadena que comienza en estado\( y \) en el tiempo 0. Esta es la observación crítica en la prueba del siguiente teorema.
Si\( x, \, y \in S \) entonces
- \(\P(N_y = 0 \mid X_0 = x) = 1 - H(x, y)\)
- \( \P(N_y = n \mid X_0 = x) = H(x, y) [H(y, y)]^{n-1}[1 - H(y, y)] \)para\( n \in \N_+ \)
Prueba
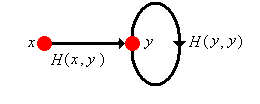
La esencia de la prueba se ilustra en el gráfico anterior. Las líneas gruesas están pensadas como recordatorios de que estas no son transiciones de un solo paso, sino que representan todos los caminos entre los vértices dados. Tenga en cuenta que en el caso especial que\( x = y \) tenemos\[ \P(N_x = n \mid X_0 = x) = [H(x, x)]^n [1 - H(x, x)], \quad n \in \N \] En todos los casos, la variable de conteo\( N_y \) tiene esencialmente una distribución geométrica, pero la distribución bien puede ser defectuosa, con parte de la masa de probabilidad en\( \infty \). El comportamiento es bastante diferente dependiendo de si\( y \) es transitorio o recurrente.
Si\( x, \, y \in S \) y\( y \) es transitorio entonces
- \( \P(N_y \lt \infty \mid X_0 = x) = 1 \)
- \( G(x, y) = H(x, y) \big/ [1 - H(y, y)] \)
- \( H(x, y) = G(x, y) \big/ [1 + G(y, y)] \)
Prueba
- Si\( y \) es transitorio entonces\( H(y, y) \lt 1 \). De ahí usando el resultado anterior y series geométricas,\[\P(N_y \in \N_+ \mid X_0 = x) = \sum_{n=1}^\infty \P(N_y = n \mid X_0 = x) = H(x, y) [1 - H(y, y)] \sum_{n=1}^\infty [H(y, y)]^{n-1} = H(x, y)\] De ahí\ comenzar {alinear*}\ P (n_y\ lt\ infty\ mid X_0 = x) & =\ P (n_y\ in\ N\ mid X_0 = x) =\ P (N_y = 0\ mid X_0 = x) +\ P (N_y\ in\ N_+\ mid X_0 = x)\\ & = [1 - H (x, y)] + H (x, y) = 1\ final {alinear*}
- Usando la derivada de la serie geométrica,\ begin {align*} G (x, y) & =\ E (N_y\ mid X_0 = x) =\ sum_ {n=1} ^\ infty n\ P (n_y = n\ mid X_0 = x)\\ & = H (x, y) [1 - H (y, y)]\ sum_ {n=1} ^\ infty n [H (y, y)] ^ {n-1} =\ frac {H (x, y)} {1 - H (y, y)}\ final {alinear*}
- De (b),\( G(y, y) = H(y, y) \big/[1 - H(y, y)] \) así resolviendo para\( H(y, y) \) da\( H(y, y) = G(y, y) \big/ [1 + G(y, y)] \). Sustituir esto de nuevo en (b) da\( G(x, y) = H(x, y)[1 + G(y, y)] \).
si\( x, \, y \in S \) y\( y \) es recurrente entonces
- \( \P(N_y = 0 \mid X_0 = x) = 1 - H(x, y) \)y\( \P(N_y = \infty \mid X_0 = x) = H(x, y) \)
- \( G(x, y) = 0 \)si\( H(x, y) = 0 \) y\( G(x, y) = \infty \) si\( H(x, y) \gt 0 \)
- \( \P(N_y = \infty \mid X_0 = y) = 1 \)y\( G(y, y) = \infty \)
Prueba
- Si\( y \) es recurrente,\( H(y, y) = 1 \) y así del resultado anterior,\( \P(N_y = n \mid X_0 = x) = 0 \) para todos\( n \in \N_+ \). De ahí\( \P(N_y = \infty \mid X_0 = x) = 1 - \P(N_y = 0 \mid X_0 = x) = 1 - H(x, y) \).
- Si\( H(x, y) = 0 \) entonces\( \P(N_y = 0 \mid X_0 = x) = 1 \), así\( \E(N_y \mid X_0 = x) = 0 \). Si\( H(x, y) \gt 0 \) entonces\( \P(N_y = \infty \mid X_0 = x) \gt 0 \) es así\( \E(N_y \mid X_0 = x) = \infty \).
- Del resultado anterior,\( \P(N_y = n \mid X_0 = y) = 0 \) para todos\( n \in \N \), así\( \P(N_y = \infty \mid X_0 = y) = 1 \).
Obsérvese que existe una relación invertible entre la matriz\( H \) y la matriz\( G \); si conocemos una podemos calcular la otra. En particular, podemos caracterizar la fugacidad o recurrencia de un estado en términos de\( G \). Aquí está nuestro resumen hasta el momento:
Vamos\( x \in S \).
- Estado\( x \) es transitorio si y sólo\( H(x, x) \lt 1 \) si y sólo si\( G(x, x) \lt \infty \).
- Estado\( x \) es recurrente si y solo\( H(x, x) = 1 \) si y solo si\( G(x, x) = \infty \).
Por supuesto, la clasificación también se mantiene para la matriz potencial\( R = I + G \). Es decir, el estado\( x \in S \) es transitorio si y solo si\( R(x , x) \lt \infty \) y el estado\( x \) es recurrente si y solo si\( R(x, x) = \infty \).
Relaciones
Las probabilidades de golpeo sugieren una relación importante en el espacio estatal\( S \).
Porque\( (x, y) \in S^2 \), decimos que\( x \) lleva a\( y \) y escribimos\( x \to y \) si cualquiera\( x = y \) o\( H(x, y) \gt 0 \).
Se deduce inmediatamente del resultado anterior que\( x \to y \) si y sólo si\( P^n(x, y) \gt 0 \) para algunos\( n \in \N \). En términos de la gráfica estatal de la cadena,\( x \to y \) si y sólo si\( x = y \) o hay un camino dirigido de\( x \) a\( y \). Obsérvese que los leads a la relación es reflexiva por definición:\( x \to x \) para cada uno\( x \in S \). La relación también tiene otra propiedad importante.
Las derivaciones a la relación es transitiva: Por\( x, \, y, \, z \in S \), si\( x \to y \) y\( y \to z \) entonces\( x \to z \).
Prueba
Si\( x \to y \) y\( y \to z \), entonces existen\( j, \, k \in N \) tal que\( P^j(x, y) \gt 0 \) y\( P^k(y, z) \gt 0 \). Pero entonces\( P^{j+k}(x, z) \ge P^j(x, y) P^k(y, z) \gt 0 \) así\( x \to z \).
Los leads a la relación sugieren naturalmente un par de otras definiciones que son importantes.
Supongamos que no\( A \subseteq S \) está vacío.
- \( A \)está cerrado si\( x \in A \) e\( x \to y \) implica\( y \in A \).
- \( A \)es irreducible si\( A \) está cerrado y no tiene subconjuntos cerrados adecuados.
Supongamos que\( A \subseteq S \) está cerrado. Entonces
- \( P_A \), la restricción de\( P \) a\( A \times A\), es una matriz de probabilidad de transición en\( A \).
- \( \bs{X} \)restringido a\( A \) es una cadena de Markov con matriz de probabilidad de transición\( P_A \).
- \( (P^n)_A = (P_A)^n \)para\( n \in \N \).
Prueba
- Si\( x \in A \) y\( y \notin A \), entonces\( x \) no lleva a\( y \) que así en particular\( P(x, y) = 0 \). De ello se deduce que\( \sum_{y \in A} P(x, y) = 1 \) para\( x \in A \) así\( P_A \) es una matriz de probabilidad de transición.
- Esto se desprende de (a). Si la cadena comienza en\( A \), entonces la cadena permanece adentro\( A \) para siempre, y por supuesto, la propiedad de Markov aún se mantiene.
- Nuevamente, esto se desprende de (a).
Por supuesto, todo el espacio estatal\( S \) está cerrado por definición. Si también es irreducible, decimos que la\( \bs{X} \) propia cadena de Markov es irreducible. Recordemos que para un subconjunto no vacío\( A \) de\( S \) y para\( n \in \N \), la notación\( P_A^n \) se refiere a\( (P_A)^n \) y no\( (P^n)_A \). En general, estos no son lo mismo, y de hecho para\( x, \, y \in A \),\[ P_A^n(x, y) = \P(X_1 \in A, \ldots, X_{n-1} \in A, X_n = y \mid X_0 = x) \] la probabilidad de pasar de\( x \) a\( y \) en\( n \) pasos, permaneciendo en\( A \) todo el tiempo. Pero si\( A \) está cerrado, entonces como se señala en la parte (c), esto es justo\( P^n(x, y) \).
Supongamos que\( A \) es un subconjunto no vacío de\( S \). Entonces\( \cl(A) = \{y \in S: x \to y \text{ for some } x \in A\} \) es el conjunto cerrado más pequeño que contiene\( A \), y se llama el cierre de\( A \). Es decir,
- \( \cl(A) \)está cerrado.
- \( A \subseteq \cl(A) \).
- Si\( B \) está cerrado y\( A \subseteq B \) luego\( \cl(A) \subseteq B \)
Prueba
- Supongamos eso\( x \in \cl(A) \) y aquello\( x \to y \). Entonces existe\( a \in A \) tal que\( a \to x \). Por la propiedad transitiva,\( a \to y \) y por lo tanto\( y \in \cl(A) \).
- Si\( x \in A \) entonces\( x \to x \) es así\( x \in \cl(A) \).
- Supongamos que\( B \) está cerrado y eso\( A \subseteq B \). Si\( x \in \cl(A) \), entonces existe\( a \in A \) tal que\( a \to x \). De ahí\( a \in B \) y\( a \to x \). Ya que\( B \) está cerrado, se deduce que\( x \in B \). De ahí\( \cl(A) \subseteq B \).
Recordemos que para un entero positivo fijo\( k \), también\( P^k \) es una matriz de probabilidad de transición, y de hecho gobierna la cadena de Markov \( k \)-step\( (X_0, X_k, X_{2 k}, \ldots) \). De ello se deduce que podríamos considerar los leads a la relación para esta cadena, y todos los resultados anteriores aún se mantendrían (relativos, por supuesto, a la cadena\( k \) -step). Ocasionalmente tendremos que considerar esta relación, por la que vamos a denotar\( \underset{k} \to \), particularmente en nuestro estudio de la periodicidad.
Supongamos que\( j, \, k \in \N_+ \). Si\( x \, \underset{k}\to \, y \) y\( j \mid k \) entonces\( x \, \underset{j}\to \, y \).
Prueba
Si\( x \, \underset{k}\to \, y \) entonces existe\( n \in \N \) tal que\( P^{n k}(x, y) \gt 0 \). Si\( j \mid k \), existe\( m \in \N_+ \) tal que\( k = m j \). De ahí\( P^{n m j}(x, y) \gt 0 \) que así\( x \, \underset{j}\to \, y \).
Al combinar los leads a la relación\( \to \) con su inverso, el viene de relación\( \leftarrow \), podemos obtener otra relación muy útil.
Porque\( (x, y) \in S^2 \), decimos eso\( x \) hacia y desde\( y \) y escribimos\( x \leftrightarrow y \) si\( x \to y \) y\( y \to x \).
Por definición, esta relación es simétrica: si\( x \leftrightarrow y \) entonces\( y \leftrightarrow x \). De nuestro trabajo anterior, también es reflexivo y transitivo. Así, la relación de ida y de origen es una relación de equivalencia. Como todas las relaciones de equivalencia, divide el espacio en clases de equivalencia mutuamente disjuntas. Denotaremos la clase de equivalencia de un estado\( x \in S \) por\[ [x] = \{y \in S: x \leftrightarrow y\} \] Así, para dos estados cualesquiera\( x, \, y \in S\), ya sea\( [x] = [y] \) o\( [x] \cap [y] = \emptyset \), y además,\( \bigcup_{x \in S} [x] = S \).
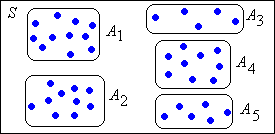
Dos resultados negativos:
- Un conjunto cerrado no es necesariamente una clase de equivalencia.
- Una clase de equivalencia no está necesariamente cerrada.
Ejemplo
Consideremos la cadena trivial de Markov con espacio de estado\( S = \{0, 1\} \) y matriz de transición\( P = \left[\begin{matrix} 0 & 1 \\ 0 & 1\end{matrix}\right] \). Entonces el estado 0 lleva determinísticamente a 1 en un paso, mientras que el estado 1 está absorbiendo. Para los leads a la relación, las únicas relaciones son\( 0 \to 0 \),\( 0 \to 1 \), y\( 1 \to 1 \). Así, las clases de equivalencia son\( \{0\} \) y\( \{1\} \).
- Todo el espacio estatal\( S \) está cerrado, pero no es una clase de equivalencia.
- \( \{0\} \)es una clase de equivalencia pero no está cerrada.
Por otro lado, tenemos el siguiente resultado:
Si\( A \subseteq S \) es irreducible, entonces\( A \) es una clase de equivalencia.
Prueba
Fix\( x \in A \) (recuerde que los conjuntos cerrados no están vacíos por definición). Ya que\( A \) está cerrado se deduce que\( [x] \subseteq A \). Ya que\( A \) es irreducible,\( \cl(y) = A \) para cada uno\( y \in A \) y en particular,\( \cl(x) = A \). De ello se deduce que\( x \leftrightarrow y \) para cada uno\( y \in A \). De ahí\( A \subseteq [x] \).
La relación de equivalencia de ida y vuelta es muy importante porque muchas propiedades estatales interesantes resultan de hecho ser propiedades de clase, compartidas por todos los estados en una clase de equivalencia dada. En particular, las propiedades de recurrencia y fugacidad son propiedades de clase.
Clases transitorias y recurrentes
Nuestro siguiente resultado es de fundamental importancia: un estado recurrente sólo puede conducir a otros estados recurrentes.
Si\( x \) es un estado recurrente y\( x \to y \) luego\( y \) es recurrente y\( H(x, y) = H(y, x) = 1 \).
Prueba
El resultado se sostiene trivialmente si\( x = y \), entonces asumimos\( x \ne y \). Dejar\( \alpha(x, y) \) denotar la probabilidad, a partir de\( x \), de que la cadena alcanza\( y \) sin un retorno intermedio a\( x \). Debe darse el caso que\( \alpha(x, y) \gt 0 \) desde\( x \to y \). En cuanto a la gráfica de\( \bs{X} \), si hay un camino de\( x \) a\( y \), entonces hay un camino de\( x \) a\( y \) sin ciclos. A partir de\( x \), la cadena podría no volver a\( x \) por llegar primero\( y \) sin un retorno intermedio a\( x \), y luego de\( y \) no llegar nunca\( x \). De las propiedades homogéneas de Markov y tiempo, se deduce que\( 1 - H(x, x) \ge \alpha(x, y)[1 - H(y, x)] \ge 0 \). Pero\( H(x, x) = 1 \) así se deduce de eso\( H(y, x) = 1 \). Entonces ahora sabemos que existen enteros positivos\( j, \, k \) tales que\( P^j(x, y) \gt 0 \) y\( P^k(y, x) \gt 0 \). De ahí que para cada\( n \in \N \),\[ P^{j + k + n}(y, y) \ge P^k(y, x) P^n(x, x) P^j(x, y) \] Recordemos que\( G(x, x) = \infty \) ya\( x \) es recurrente. Por lo tanto, la suma\( n \) en la ecuación mostrada da\( G(y, y) = \infty \). De ahí\( y \) que sea recurrente. Por último, revertir los roles de\( x \) y\( y \), si sigue eso\( H(x, y) = 1 \)
Del último teorema, tenga en cuenta que si\( x \) es recurrente, entonces todos los estados en también\( [x] \) son recurrentes. Así, para cada clase de equivalencia, o bien todos los estados son transitorios o todos los estados son recurrentes. Por lo tanto, podemos referirnos a clases transitorias o recurrentes así como a estados.
Si\( A \) es una clase de equivalencia recurrente entonces\( A \) es irreducible.
Prueba
Supongamos eso\( x \in A \) y aquello\( x \to y \). Ya que\( x \) es recurrente, también\( y \) es recurrente y\( y \to x \). De ahí\( x \leftrightarrow y \) y así\( y \in A \) ya\( A \) es una clase de equivalencia. Supongamos que\( B \subseteq A \) está cerrado. Ya que no\( B \) está vacío por definición, existe\( x \in B \) y así\( x \in A \) también. Por cada\( y \in A \),\( x \leftrightarrow y \) así\( y \in B \) ya que\( B \) está cerrado. \( A = B \)Así\( A \) es irreducible.
Si\( A \) es finito y cerrado entonces\( A \) tiene un estado recurrente.
Prueba
Arreglar\( x \in A \). Ya que\( A \) está cerrado, se deduce que\( \P(N_A = \infty \mid X_0 = x) = 1 \). Ya que\( A \) es finito, se deduce que\( \P(N_y = \infty \mid X_0 = x) \gt 0 \) para algunos\( y \in A \). Pero entonces\( y \) es recurrente.
Si\( A \) es finito e irreducible entonces\( A \) es una clase de equivalencia recurrente.
Prueba
Tenga en cuenta que\( A \) es una clase de equivalencia por un resultado anterior, y\( A \) tiene un estado recurrente por resultado anterior. De ello se deduce que todos los estados en\( A \) son recurrentes.
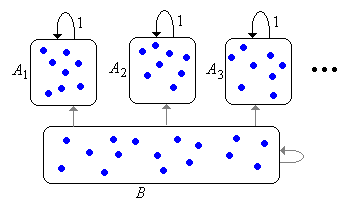
Así, la cadena de Markov\( \bs{X} \) tendrá una colección (posiblemente vacía) de clases de equivalencia recurrente\( \{A_j: j \in J\} \) donde\( J \) es un conjunto de índices contables. Cada uno\( A_j \) es irreducible. Dejar\( B \) denotar el conjunto de todos los estados transitorios. El conjunto\( B \) puede estar vacío o puede consistir en varias clases de equivalencia, pero la estructura de clases de generalmente no\( B \) es importante para nosotros. Si la cadena comienza en\( A_j \) para algunos\( j \in J \) entonces la cadena permanece\( A_j \) para siempre, visitando cada estado infinitamente a menudo con probabilidad 1. Si la cadena comienza en\( B \), entonces la cadena puede quedarse\( B \) para siempre (pero solo si\( B \) es infinita) o puede ingresar a una de las clases recurrentes\( A_j \), nunca para escapar. Sin embargo, en cualquier caso, la cadena visitará un estado transitorio dado solo finitamente muchas veces con probabilidad 1. Esta estructura básica se conoce como la descomposición canónica de la cadena, y se muestra en forma gráfica a continuación. Los bordes de\( B \) están en gris para indicar que estas transiciones pueden no existir.
Probabilidades de permanencia y una prueba de clasificación
Supongamos que\( A \) es un subconjunto apropiado de\( S \). Entonces
- \(P_A^n(x, A) = \P(X_1 \in A, X_2 \in A, \ldots, X_n \in A \mid X_0 = x) \)para\( x \in A \)
- \( \lim_{n \to \infty} P_A^n(x, A) = \P(X_1 \in A, X_2 \in A \ldots \mid X_0 = x) \)para\( x \in A \)
Prueba
Recordemos que eso\( P_A^n \) significa\( (P_A)^n \) dónde\( P_A \) está la restricción de\( P \) a\( A \times A \).
- Esto es consecuencia de la propiedad de Markov, y es la probabilidad de que la cadena permanezca en al\( A \) menos a través del tiempo\( n \), comenzando en\( x \in A \).
- Esto se desprende de (a) y el teorema de continuidad para eventos decrecientes. Esta es la probabilidad de que la cadena se quede\( A \) para siempre, comenzando en\( x \in A \).
Dejar\( g_A \) denotar la función definida por la parte (b), de manera que\[ g_A(x) = \P(X_1 \in A, X_2 \in A, \ldots \mid X_0 = x), \quad x \in A \] La función de probabilidad de permanencia\( g_A \) es un interesante complemento a la matriz de golpeo estudiada anteriormente. El siguiente resultado caracteriza esta función y proporciona un método que se puede utilizar para calcularla, al menos en algunos casos.
Porque\( A \subset S \),\( g_A \) es la función más grande en la\( A \) que toma valores\( [0, 1] \) y satisface\( g = P_A g \). Además, ya sea\( g_A = \bs{0}_A \) o\( \sup\{g_A(x): x \in A\} = 1 \).
Prueba
Tenga en cuenta que\( P_A^{n+1} \bs{1}_A = P_A P_A^n \bs{1}_A\) para\( n \in \N \). Tomando el límite como\( n \to \infty \) y usando el teorema de convergencia acotada da\( g_A = P_A g_A \). Supongamos ahora que\( g \) es una función sobre la\( A \) que toma valores\( [0, 1] \) y satisface\( g = P_A g \). Entonces\( g \le \bs{1}_A \) y por lo tanto\( g \le P_A^n \bs{1}_A \) para todos\( n \in \N \). Dejar que\( n \to \infty \) se deduce de eso\( g \le g_A \). A continuación, vamos\( c = \sup\{g_A(x): x \in A\} \). Entonces\( g_A \le c \, \bs{1}_A \) y por lo tanto\( g_A \le c \, P_A^n \bs{1}_A \) para cada uno\( n \in \N \). Dejar\( n \to \infty \) da\( g_A \le c \, g_A \). De ello se deduce que\( g_A = \bs{0}_A \) o bien\( c = 1 \).
Obsérvese que la caracterización en el último resultado incluye una ley de tipo cero-uno: o bien la probabilidad de que la cadena permanezca para\( A \) siempre es 0 para cada estado inicial\( x \in A \), o podemos encontrar estados en\( A \) los que la probabilidad sea arbitrariamente cercana a 1. Los siguientes dos resultados exploran la relación entre la función de permanencia y la recurrencia.
Supongamos que\( \bs{X} \) es una cadena irreducible, recurrente con espacio estatal\( S \). Entonces\( g_A = \bs{0}_A \) para cada subconjunto adecuado\( A \) de\( S \).
Prueba
Arreglar\( y \notin A \) y anotar eso\( 0 \le g_A(x) \le 1 - H(x, y) \) para cada\( x \in A \). Pero\( H(x, y) = 1 \) como la cadena es irreducible y recurrente. De ahí\( g_A(x) = 0 \) para\( x \in A \).
Supongamos que\( \bs{X} \) es una cadena irreducible de Markov con espacio de estado\( S \) y matriz de probabilidad de transición\( P \). Si existe un estado\( x \) tal que\( g_A = \bs{0}_A \) donde\( A = S \setminus \{x\} \), entonces\( \bs{X} \) es recurrente.
Prueba
Con\( A \) lo definido anteriormente, tenga en cuenta que\(1 - H(x, x) = \sum_{y \in A} P(x, y) g_A(y) \). De ahí\( H(x, x) = 1 \) que así\( x \) sea recurente. Dado que el\( \bs{X} \) es irreducible, se deduce que\( \bs{X} \) es recurrente.
De manera más general, supongamos que\( \bs{X} \) es una cadena de Markov con espacio de estado\( S \) y matriz de probabilidad de transición\( P \). Los dos últimos teoremas pueden ser utilizados para probar si una clase de equivalencia irreducible\( C \) es recurrente o transitoria. Arreglamos un estado\( x \in C \) y establecemos\( A = C \setminus \{x\} \). Luego tratamos de resolver la ecuación\( g = P_A g \) sobre\( A \). Si la única solución que toma valores\( [0, 1] \) es\( \bs{0}_A \), entonces la clase\( C \) es recurrente por el resultado anterior. Si hay soluciones no triviales, entonces\( C \) es transitoria. A menudo tratamos de elegir\( x \) para facilitar los cálculos.
Computación de Probabilidades y Potenciales de Golpear
Ahora sabemos bastante sobre las cadenas de Markov, y a menudo podemos clasificar los estados y calcular cantidades de interés. Sin embargo, aún no sabemos cómo calcular:
- \( G(x, y) \)cuando\( x \) y\( y \) son transitorios
- \( H(x, y) \)cuando\( x \) es transitorio y\( y \) es transitorio o recurrente.
Estos problemas están relacionados, por la relación inversa general entre la matriz\( H \) y la matriz\( G \) señalada en nuestra discusión anterior. Como es habitual, supongamos que\( \bs{X} \) es una cadena de Markov con espacio de estado\( S \), y vamos a\( B \) denotar el conjunto de estados transitorios. El siguiente resultado muestra cómo calcular\( G_B \), la matriz\( G \) restringida a los estados transitorios. Recordemos que los valores de esta matriz son finitos.
\( G_B \)satisface la ecuación\( G_B = P_B + P_B G_B \) y es la solución no negativa más pequeña. Si\( B \) es finito entonces\( G_B = (I_B - P_B)^{-1} P_B \).
Prueba
Primero tenga en cuenta\( (P^n)_B = (P_B)^n \) que una ruta entre dos estados transitorios solo puede pasar por otros estados transitorios. Así\( G_B = \sum_{n=1}^\infty P_B^n \). Del teorema de la convergencia monótona se deduce que\( P_B G_B = G_B - P_B \). Supongamos ahora que\( U \) es una matriz no negativa sobre la\( B \) satisfacción\( U = P_B + P_B U \). Entonces\( U = \sum_{k=1}^n P_B^k + P_B^{n+1} U \) para cada uno\( n \in \N_+\). De ahí\( U \ge \sum_{k=1}^n P_B^k \) para todos\( n \in \N_+ \) y por lo tanto\( U \ge G_B \). De ello se deduce que\( (I_B - P_B)(I_B + G_B) = I_B \). Si\( B \) es finita, la matriz\( I_B - P_B \) es invertible.
Ahora que podemos calcular\( G_B \), también podemos calcular\( H_B \) usando el resultado anterior. Todo lo que queda es para nosotros calcular la probabilidad de golpeo\( H(x, y) \) cuando\( x \) es transitorio y\( y \) recurrente. Lo primero que hay que notar es que la probabilidad de golpear es una propiedad de clase.
Supongamos que\( x \) es transitorio y que\( A \) es una clase recurrente. Entonces\( H(x, y) = H(x, A) \) para\( y \in A \).
Es decir, comenzando en el estado transitorio\( x \in S \), la probabilidad de golpeo a\( y \) es constante para\( y \in A \), y es solo la probabilidad de golpeo a la clase\( A \). Como antes, vamos a\( B \) denotar el conjunto de estados transitorios y supongamos que\( A \) es una clase de equivalencia recurrente. Let\( h_A \) denotar la función on\( B \) que da la probabilidad de golpeo a la clase\( A \), y vamos\( p_A \) denotar la función on\( B \) que da la probabilidad de entrar\( A \) en el primer paso:\[ h_A(x) = H(x, A), \; p_A(x) = P(x, A), \quad x \in B \]
\( h_A = p_A + G_B p_A \).
Prueba
Primero tenga en cuenta que\( \P(\tau_A = n \mid X_0 = x) = (P_B^{n-1} p_A)(x) \) para\( n \in \N_+ \). A continuación, el resultado sigue sumando\( n \).
Este resultado es adecuado si ya hemos calculado\( G_B \) (usando el resultado anterior, por ejemplo). Sin embargo, tal vez solo queramos calcular\( h_A \) directamente.
\( h_A \)satisface la ecuación\( h_A = p_A + P_B h_A \) y es la solución no negativa más pequeña. Si\( B \) es finito,\( h_A = (I_B - P_B)^{-1} p_A \).
Prueba
Primero, condicionar en\( X_1 \) da\( h_A = p_A + P_B h_A \). Siguiente supongamos que no\( h \) es negativo y satisface\( h = p_A + P_B h \). Entonces\( h = p_A + \sum_{k=1}^{n-1} P_B^k p_A + P_B^n h \) para cada uno\( n \in \N_+ \). De ahí\( h \ge p_A + \sum_{k=1}^{n-1} P_B^k p_A \). Dejar\( n \to \infty \) da\( h \ge h_A \). La representación cuando\( B \) es finita se desprende del resultado anterior.
Ejemplos y Aplicaciones
Cadenas Finitas
Considere una cadena de Markov con espacio de estado\( S = \{a, b, c, d\} \) y matriz de transición\( P \) que se da a continuación:
\[ P = \left[ \begin{matrix} \frac{1}{2} & \frac{2}{3} & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \end{matrix} \right] \]- Dibuja la gráfica estatal.
- Encuentra las clases equivalentes y clasifica cada una como transitoria o recurrente.
- Compute la matriz\( G \).
- Compute la matriz\( H \).
Contestar
-
Gráfica estatal 
- \( \{a, b\} \)recurrente;\( \{c\} \) recurrente;\( \{d\} \) transitorio.
- \( G = \left[ \begin{matrix} \infty & \infty & 0 & 0 \\ \infty & \infty & 0 & 0 \\ 0 & 0 & \infty & 0 \\ \infty & \infty & \infty & \frac{1}{3} \end{matrix} \right] \)
- \( H = \left[ \begin{matrix} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \frac{2}{3} & \frac{2}{3} & \frac{1}{3} & \frac{1}{4} \end{matrix} \right] \)
Considere una cadena de Markov con espacio de estado\( S = \{1, 2, 3, 4, 5, 6\} \) y matriz de transición\( P \) que se da a continuación:
\[ P = \left[ \begin{matrix} 0 & 0 & \frac{1}{2} & 0 & \frac{1}{2} & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \frac{1}{4} & 0 & \frac{1}{2} & 0 & \frac{1}{4} & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 & \frac{2}{3} & 0 \\ 0 & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & 0 & \frac{1}{4} \end{matrix} \right] \]- Dibuje la gráfica del estado.
- Encuentra las clases de equivalencia y clasifica cada una como recurrente o transitoria.
- Compute la matriz\( G \).
- Compute la matriz\( H \).
Contestar
-
Gráfica estatal 
- \( \{1, 3, 5\} \)recurrente;\( \{2, 6\} \) transitorio;\( \{4\} \) recurrente.
- \( G = \left[ \begin{matrix} \infty & 0 & \infty & 0 & \infty & 0 \\ \infty & \frac{1}{2} & \infty & \infty & \infty & 2 \\ \infty & 0 & \infty & 0 & \infty & 0 \\ 0 & 0 & 0 & \infty & 0 & 0 \\ \infty & 0 & \infty & 0 & \infty & 0 \\ \infty & \frac{1}{2} & \infty & \infty & \infty & 1 \end{matrix} \right] \)
- \( H = \left[ \begin{matrix} 1 & 0 & 1 & 0 & 1 & 0 \\ \frac{1}{2} & \frac{1}{3} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ \frac{1}{2} & \frac{1}{3} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix} \right] \)
Considere una cadena de Markov con espacio de estado\( S = \{1, 2, 3, 4, 5, 6\} \) y matriz de transición\( P \) que se da a continuación:
\[ P = \left[ \begin{matrix} \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 \\ \frac{1}{4} & \frac{3}{4} & 0 & 0 & 0 & 0 \\ \frac{1}{4} & 0 & \frac{1}{2} & \frac{1}{4} & 0 & 0 \\ \frac{1}{4} & 0 & \frac{1}{4} & \frac{1}{4} & 0 & \frac{1}{4} \\ 0 & 0 & 0 & 0 & \frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 0 & 0 & \frac{1}{2} & \frac{1}{2} \end{matrix} \right] \]- Dibuje la gráfica del estado.
- Encuentra las clases de equivalencia y clasifica cada una como recurrente o transitoria.
- Compute la matriz\( G \).
- Compute la matriz\( H \).
Contestar
-
Gráfica estatal 
- \( \{1, 2\} \)recurrente;\( \{3, 4\} \) transitorio;\( \{5, 6\} \) recurrente.
- \( G = \left[ \begin{matrix} \infty & \infty & 0 & 0 & 0 & 0 \\ \infty & \infty & 0 & 0 & 0 & 0 \\ \infty & \infty & \frac{7}{5} & \frac{4}{5} & \infty & \infty \\ \infty & \infty & \frac{4}{5} & \frac{3}{5} & \infty & \infty \\ 0 & 0 & 0 & 0 & \infty & \infty \\ 0 & 0 & 0 & 0 & \infty & \infty \end{matrix} \right] \)
- \( H = \left[ \begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 \\ \frac{4}{5} & \frac{4}{5} & \frac{7}{12} & \frac{1}{2} & \frac{1}{5} & \frac{1}{5} \\ \frac{3}{5} & \frac{3}{5} & \frac{1}{3} & \frac{3}{8} & \frac{2}{5} & \frac{2}{5} \\ 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 \end{matrix} \right] \)
Modelos Especiales
Vuelva a leer las definiciones de las cadenas Ehrenfest y las cadenas Bernoulli-Laplace. Obsérvese que dado que estas cadenas son irreducibles y tienen espacios de estado finitos, son recurrentes.
Lea la discusión sobre recurrencia en la sección sobre las cadenas de confiabilidad.
Lee la discusión sobre caminatas aleatorias\( \Z^k \) en la sección sobre las caminatas aleatorias en gráficas.
Lee la discusión sobre extinción y explosión en la sección sobre la cadena de ramificación.
Lea la discusión sobre recurrencia y fugacidad en la sección sobre cadenas de colas.
Lea la discusión sobre recurrencia y fugacidad en la sección sobre cadenas de nacimiento y muerte.


