16.8: Las cadenas de Ehrenfest

\(\newcommand{\P}{\mathbb{P}}\)\(\newcommand{\E}{\mathbb{E}}\)\(\newcommand{\R}{\mathbb{R}}\)\(\newcommand{\N}{\mathbb{N}}\)\(\newcommand{\Z}{\mathbb{Z}}\)\(\newcommand{\bs}{\boldsymbol}\)\( \newcommand{\cl}{\text{cl}} \)

Teoría Básica

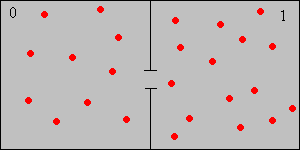
Las cadenas de Ehrenfest, llamadas así por Paul Ehrenfest, son modelos simples y discretos para el intercambio de moléculas de gas entre dos contenedores. Sin embargo, pueden formularse como simples modelos de bolas y urnas; las bolas corresponden a las moléculas y las urnas a los dos contenedores. Así, supongamos que tenemos dos urnas, etiquetadas 0 y 1, que contienen un total de\( m \) bolas. El estado del sistema en el momento\( n \in \N \) es el número de bolas en la urna 1, que denotaremos por\( X_n \). Nuestro proceso estocástico es\( \bs{X} = (X_0, X_1, X_2, \ldots) \) con el espacio estatal\( S = \{0, 1, \ldots, m\} \). Por supuesto, el número de bolas en la urna 0 a la vez\( n \) es\( m - X_n \).

Los modelos

En el modelo básico de Ehrenfest, en cada unidad de tiempo discreta, independientemente del pasado, se selecciona una bola al azar y se mueve a la otra urna.

Figura\(\PageIndex{1}\): El modelo Ehrenfest

\( \bs{X} \)es una cadena de Markov en tiempo discreto\( S \) con matriz de probabilidad de transición\( P \) dada por\[ P(x, x - 1) = \frac{x}{m}, \; P(x, x + 1) = \frac{m - x}{m}, \quad x \in S \]

Prueba

Daremos una construcción de la cadena a partir de un proceso más básico. Dejar\( V_n \) ser la pelota seleccionada en el momento\( n \in \N_+ \). Así\( \bs{V} = (V_1, V_2, \ldots) \) es una secuencia de variables aleatorias independientes, cada una distribuida uniformemente en\( \{1, 2, \ldots, m\} \). Seamos\( X_0 \in S \) independientes de\( \bs{V} \). (Podemos iniciar el proceso de la manera que nos guste). Ahora defina el proceso de estado recursivamente de la siguiente manera:\[ X_{n+1} = \begin{cases} X_n - 1, & V_{n+1} \le X_n \\ X_n + 1, & V_{n+1} \gt X_n \end{cases}, \quad n \in \N \]

En el experimento de Ehrenfest, seleccione el modelo básico. Para valores seleccionados\( m \) y valores seleccionados del estado inicial, ejecute la cadena por 1000 pasos de tiempo y anote el comportamiento limitante de la proporción de tiempo empleado en cada estado.

Supongamos ahora que modificamos el modelo básico de Ehrenfest de la siguiente manera: en cada momento discreto, independientemente del pasado, seleccionamos una bola al azar y una urna al azar. Después colocamos la bola elegida en la urna elegida.

\( \bs{X} \)es una cadena de Markov en tiempo discreto\( S \) con la matriz de probabilidad de transición\( Q \) dada por\[ Q(x, x - 1) = \frac{x}{2 m}, \; Q(x, x) = \frac{1}{2}, \; Q(x, x + 1) = \frac{m - x}{2 m}, \quad x \in S \]

Prueba

Nuevamente, podemos construir la cadena a partir de un proceso más básico. Dejar\( X_0 \) y\( \bs{V} \) ser como en el Teorema 1. Deja\( U_n \) ser la urna seleccionada a la hora\( n \in \N_+ \). Así\( \bs{U} = (U_1, U_2, \ldots) \) es una secuencia de variables aleatorias independientes, cada una distribuida uniformemente en\( \{0, 1\} \) (así que\( \bs{U} \) es una secuencia de ensayos de Bernoulli justa). Además,\( \bs{U} \) es independiente de\( \bs{V} \) y\( X_0 \). Ahora defina el proceso de estado recursivamente de la siguiente manera:\[ X_{n+1} = \begin{cases} X_n - 1, & V_{n+1} \le X_n, \; U_{n+1} = 0 \\ X_n + 1, & V_{n+1} \gt X_n, \; U_{n+1} = 1 \\ X_n, & \text{otherwise} \end{cases}, \quad n \in \N \]

Tenga en cuenta que\( Q(x, y) = \frac{1}{2} P(x, y) \) para\( y \in \{x - 1, x + 1\} \).

En el experimento de Ehrenfest, seleccione el modelo modificado. Para valores seleccionados\( m \) y valores seleccionados del estado inicial, ejecute la cadena por 1000 pasos de tiempo y anote el comportamiento limitante de la proporción de tiempo empleado en cada estado.

Clasificación

Las cadenas básicas y modificadas de Ehrenfest son irreducibles y recurrentes positivas.

Prueba

Las cadenas son claramente irreducibles ya que cada estado conduce a cada otro estado. De ello se deduce que las cadenas son recurrentes positivas ya que el espacio estatal\( S \) es finito.

La cadena básica de Ehrenfest es periódica con periodo 2. Las clases cíclicas son el conjunto de estados pares y el conjunto de estados impares. La matriz de transición de dos pasos es

\[ P^2(x, x - 2) = \frac{x (x - 1)}{m^2}, \; P^2(x, x) = \frac{x(m - x + 1) + (m - x)(x + 1)}{m^2}, \; P^2(x, x + 2) = \frac{(m - x)(m - x - 1)}{m^2}, \quad x \in S \]

Prueba

Tenga en cuenta que los retornos a un estado solo pueden ocurrir en momentos pares, por lo que la cadena tiene periodo 2. La forma de\( P^2 \) se desprende de la fórmula\( P \) anterior.

La cadena Ehrenfest modificada es aperiódica.

Prueba

Tenga en cuenta que\( P(x, x) \gt 0 \) para cada uno\( x \in S \).

Distribuciones invariantes y limitantes

Para las cadenas de Ehrenfest básica y modificada, la distribución invariante es la distribución binomial con parámetro de ensayo\( m \) y parámetro de éxito\( \frac{1}{2} \). Entonces, la función de densidad de probabilidad invariante\( f \) viene dada por\[ f(x) = \binom{m}{x} \left( \frac{1}{2} \right)^m, \quad x \in S \]

Prueba

Para la cadena básica tenemos\ begin {align*} (f P) (y) & = f (y - 1) P (y - 1, y) + f (y + 1) P (y + 1, y)\\ & =\ binom {m} {y - 1}\ left (\ frac {1} {2}\ right) ^m\ frac {m - y + 1} {m} +\ binom {m} {y + 1}\ izquierda (\ frac {1} {2}\ derecha) ^m\ frac {y + 1} {m}\\ & =\ izquierda (\ frac {1} {2}\ derecha) ^m\ izquierda [\ binom {m - 1} {y - 1} +\ binom { m - 1} {y}\ right] =\ left (\ frac {1} {2}\ right) ^m\ binom {m} {y} = f (y),\ quad y\ in S\ end {align*} El último paso utiliza una identidad fundamental para los coeficientes binomiales. Para la cadena modificada podemos usar el resultado para la cadena básica:\ begin {align*} (f Q) (y) & = f (y - 1) Q (y - 1, y) + f (y) Q (y, y) + f (y + 1) Q (y + 1, y)\\ & =\ frac {1} {2} f (y - 1) P (y - 1, y) +\ frac {1} {2} f (y + 1) P (y + 1, y) +\ frac {1} {2} f (y) = f (y),\ quad y\ en S\ final {alinear*}

Así, la distribución invariante corresponde a colocar cada bola de forma aleatoria e independiente ya sea en la urna 0 o en la urna 1.

El tiempo medio de retorno al estado\( x \in S \) para la cadena Ehrenfest básica o modificada es\( \mu(x) = 2^m \big/ \binom{m}{x} \).

Prueba

Esto se desprende de la teoría general y de la distribución invariante anterior.

Para la cadena básica de Ehrenfest, el comportamiento limitante de la cadena es el siguiente:

1. \( P^{2 n}(x, y) \to \binom{m}{y} \left(\frac{1}{2}\right)^{m-1} \)como\( n \to \infty \) si\( x, \, y \in S \) tuvieran la misma paridad (ambos pares o ambos impares). El límite es 0 en caso contrario.
2. \( P^{2 n+1}(x, y) \to \binom{m}{y} \left(\frac{1}{2}\right)^{m-1} \)como\( n \to \infty \) si\( x, \, y \in S \) tuvieran paridad de oposición (uno par y otro impar). El límite es 0 en caso contrario.

Prueba

Estos resultados se derivan de la teoría general y la distribución invariante anterior, y el hecho de que la cadena es periódica con el periodo 2, con los enteros impares y pares\( S \) como las clases cíclicas.

Para la cadena Ehrenfest modificada, en\( Q^n(x, y) \to \binom{m}{y} \left(\frac{1}{2}\right)^m \)\( n \to \infty \) cuanto a\( x, \, y \in S \).

Prueba

Nuevamente, esto se desprende de la teoría general y la distribución invariante anterior, y el hecho de que la cadena es aperiódica.

En el experimento de Ehrenfest, la distribución binomial limitante se muestra gráfica y numéricamente. Para cada modelo y para valores seleccionados\( m \) y valores seleccionados del estado inicial, ejecute la cadena por 1000 pasos de tiempo y anote el comportamiento limitante de la proporción de tiempo empleado en cada estado. ¿Cómo las elecciones\( m \), el estado inicial y el modelo parecen afectar la tasa de convergencia a la distribución limitante?

Reversibilidad

Las cadenas básicas y modificadas de Ehrenfest son reversibles.

Prueba

Dejemos\( g(x) = \binom{m}{x} \) para\( x \in S \). Las observaciones cruciales son\( g(x) P(x, y) = g(y) P(y, x)\) y\(g(x) Q(x, y) = g(y) Q(y, x)\) para todos\( x, \, y \in S \). Para la cadena básica, si\( x \in S \) entonces\ comienza {alinear*} g (x) P (x, x - 1) & = g (x - 1) P (x - 1, x) =\ binom {m - 1} {x - 1}\\ g (x) P (x, x + 1) & = g (x + 1) P (x + 1, x) =\ binom {m - 1} {x}\ end {align*} En todos los demás casos,\( g(x) P(x, y) = g(y) P(y, x) = 0 \). La condición de reversibilidad para la cadena modificada sigue trivialmente de la de la cadena básica ya que\( Q(x, y) = \frac{1}{2} P(x, y) \) para\( y = x \pm 1 \) (y por supuesto la condición de reversibilidad se cumple trivialmente cuando\( x = y \)). Tenga en cuenta que el PDF invariante\( f \) es simplemente\( g \) normalizado. La condición de reversibilidad da otra (y mejor) prueba que\( f \) es invariante.

Ejecutar la simulación del experimento Ehrenfest 10,000 pasos de tiempo para cada modelo, para valores seleccionados de\( m \), y con estado inicial 0. Tenga en cuenta que al principio, se puede ver la flecha del tiempo. Después de un largo periodo, sin embargo, la dirección del tiempo ya no es evidente.

Ejercicios Computacionales

Considera la cadena básica de Ehrenfest con\( m = 5 \) bolas, y supongamos que\( X_0 \) tiene la distribución uniforme puesta\( S \).

1. Calcular la función de densidad de probabilidad, media y varianza de\( X_1 \).
2. Calcular la función de densidad de probabilidad, media y varianza de\( X_2 \).
3. Calcular la función de densidad de probabilidad, media y varianza de\( X_3 \).
4. Esboce la función de densidad de probabilidad inicial y las funciones de densidad de probabilidad en las partes (a), (b) y (c) en un conjunto común de ejes.

Contestar

1. \( f_1 = \left( \frac{1}{30}, \frac{7}{30}, \frac{7}{30}, \frac{7}{30}, \frac{7}{30}, \frac{1}{30} \right) \),\( \mu_1 = \frac{5}{2} \),\(\sigma_1^2 = \frac{19}{12} \)
2. \( f_2 = \left( \frac{7}{150}, \frac{19}{150}, \frac{49}{150}, \frac{49}{150}, \frac{19}{150}, \frac{7}{150} \right) \),\( \mu_2 = \frac{5}{2} \),\(\sigma_2^2 = \frac{79}{60} \)
3. \( f_3 = \left( \frac{19}{750}, \frac{133}{750}, \frac{223}{150}, \frac{223}{150}, \frac{133}{150}, \frac{19}{150} \right) \),\( \mu_2 = \frac{5}{2} \),\(\sigma_3^2 = \frac{431}{300} \)

Considere la cadena Ehrenfest modificada con\( m = 5 \) bolas, y supongamos que la cadena comienza en el estado 2 (con probabilidad 1).

1. Calcular la función de densidad de probabilidad, media y desviación estándar de\( X_1 \).
2. Calcular la función de densidad de probabilidad, media y desviación estándar de\( X_2 \).
3. Calcular la función de densidad de probabilidad, media y desviación estándar de\( X_3 \).
4. Esboce la función de densidad de probabilidad inicial y las funciones de densidad de probabilidad en las partes (a), (b) y (c) en un conjunto común de ejes.

Contestar

1. \( f_1 = (0, 0.2, 0.5, 0.3, 0, 0) \),\( \mu_1 = 2.1 \),\(\sigma_1 = 0.7 \)
2. \( f_2 = (0.02, 0.20, 0.42, 0.30, 0.06, 0) \),\( \mu_2 = 2.18 \),\(\sigma_2 = 0.887 \)
3. \( f_3 = (0.030, 0.194, 0.380, 0.300, 0.090, 0.006) \),\( \mu_3 = 2.244 \),\(\sigma_3 = 0.984 \)