1.2: Sistemas de Probabilidad
- Page ID
- 150995
Medidas de probabilidad
En el módulo "Probabilidad" se introduce la noción de un espacio básico ΩΩ de todos los posibles resultados de un ensayo o experimento, eventos como subconjuntos del espacio básico determinados por las características apropiadas de los resultados, y combinaciones lógicas o booleanas de los eventos (uniones, intersecciones, y complementos) correspondientes a combinaciones lógicas de las características definitorias.
La ocurrencia o no ocurrencia de un evento está determinada por las características o atributos del resultado observado en un ensayo. La realización del ensayo se visualiza como seleccionar un resultado del conjunto básico. Un evento ocurre siempre que el resultado seleccionado es un miembro del subconjunto que representa el evento. Como se ha descrito hasta ahora, el proceso de selección podría ser bastante deliberado, con un resultado prescrito, o podría implicar las incertidumbres asociadas con el “azar”. La probabilidad entra en el cuadro sólo en esta última situación. Antes de que se realice el juicio, existe incertidumbre sobre cuál de estas posibilidades latentes se realizará. Tradicionalmente, la probabilidad es un número asignado a un evento que indica la probabilidad de que ocurra ese evento en cualquier ensayo.
Comenzamos por mirar el modelo clásico que primero formuló con éxito ideas de probabilidad en forma matemática. Utilizamos terminología y notación modernas para describirlo.
Probabilidad clásica
- El espacio básico\(\Omega\) consiste en un número finito N de posibles resultados.
-Hay treinta y seis posibles resultados de lanzar dos dados.
-Hay\(C(52,5) = \dfrac{52!}{5! 47!} = 2598960\) diferentes manos de cinco cartas (orden no importante).
-Hay\(2^5 = 32\) resultados (secuencias de cabezas o colas) de voltear cinco monedas. - A cada resultado posible se le asigna una probabilidad 1/\(N\)
- Si el evento (subconjunto)\(A\) tiene\(N_A\) elementos, entonces el evento de probabilidad asignado\(A\) es
\(P(A) = N_A /N\)(es decir, la fracción favorable a\(A\))
Con esta definición de probabilidad, a cada evento\(A\) se le asigna una probabilidad única, que puede determinarse mediante el conteo\(N_A\), el número de elementos en\(A\) (en el lenguaje clásico, el número de resultados “favorables” al evento) y\(N\) el número total de resultados posibles en el evento seguro\(\Omega\).
Probabilidades para manos de tarjetas
Considera el experimento de dibujar una mano de cinco cartas de una baraja ordinaria de 52 naipes. El número de resultados, como se señaló anteriormente, es\(N = C(52,5) = 2598960 N = C(52,5) = 2598960\). ¿Cuál es la probabilidad de dibujar una mano con exactamente dos ases? ¿Cuál es la probabilidad de dibujar una mano con dos o más ases? ¿Cuál es la probabilidad de no más de un as?
Solución
\(A\)Sea el evento de exactamente dos ases,\(B\) sea el evento de exactamente tres ases, y\(C\) sea el evento de exactamente cuatro ases. En el primer problema, debemos contar el número\(N_A\) de formas de dibujar una mano con dos ases. Seleccionamos dos ases de los cuatro, y seleccionamos las otras tres cartas de los 48 no ases. Así
\(N_A = C(4, 2) C(48,3) = 103776\), de manera que\(P(A) = \dfrac{N_A}{N} = \dfrac{103776}{2598960} \approx 0.0399\)
Hay dos o más ases si hay exactamente dos o exactamente tres o exactamente cuatro. Así, el suceso\(D\) de dos o más es\(D = A \bigvee B \bigvee C\), puesto que\(A, B, C\) son mutuamente excluyentes,
\(N_D = N_A + N_b + N_c = C(4, 2) C(48, 3) + C(4, 3) C(48, 2) + C(4, 4) C(48, 1) = 103776 + 4512 + 48 = 108336\)
para que\(P(D) \approx 0.0417\). Hay un as o ninguno si no hay dos o más ases. Así queremos\(P(D^c)\). Ahora el número en\(D_c\) es el número no en el\(D\) que está\(N - N_D\), de modo que
\(P(D^c) = \dfrac{N - N_D}{N} = 1 - \dfrac{N_D}{N} = 1 - P(D) = 0.9583\)
Este ejemplo ilustra varias propiedades importantes de la probabilidad clásica.
\(P(A) = N_A / N\)es una cantidad no negativa.
\(P(\Omega) = N/N = 1\)
Si\(A, B, C\) son mutuamente excluyentes, entonces el número en la unión disjunta es la suma de los números en los eventos individuales, de manera que
\(P(A \bigvee B \bigvee C) = P(A) + P(B) + P(C)\)
Se pueden identificar otras propiedades elementales de la probabilidad clásica. Resulta que se pueden derivar de estos tres. Aunque el modelo clásico es muy útil, y se ha desarrollado una teoría extensa, no es realmente satisfactorio para muchas aplicaciones (el problema de las comunicaciones, por ejemplo). Buscamos un modelo más general que incluya la probabilidad clásica como caso especial y, por lo tanto, sea una extensión de la misma. Adoptamos el modelo Kolmogorov (introducido por el matemático ruso A. N. Kolmogorov) que captura las ideas esenciales de una manera notablemente exitosa. Por supuesto, ningún modelo es nunca completamente exitoso. La realidad siempre parece escapar de nuestras redes lógicas.
El modelo de Kolmogorov se basa en la teoría de medidas abstractas. Una explicación completa requiere un nivel de sofisticación matemática inapropiado para un tratamiento como este. Pero la mayoría de los conceptos y muchos de los resultados son elementales y de fácil comprensión. Y muchas consideraciones matemáticas técnicas no son importantes para las aplicaciones a nivel de este tratamiento introductorio y pueden ser ignoradas. Tomamos prestados de la teoría de medidas algunos hechos clave que son o bien muy plausibles o que pueden entenderse a nivel práctico. Esto nos permite utilizar un sistema matemático muy poderoso para representar problemas prácticos de manera que conduzca tanto a la perspicacia como a estrategias útiles de solución.
Nuestro enfoque es comenzar con la noción de eventos como conjuntos introducidos anteriormente, luego introducir la probabilidad como un número asignado a eventos sujetos a ciertas condiciones que se convierten en propiedades definitivas. Poco a poco introducimos y utilizamos conceptos adicionales para construir progresivamente una disciplina poderosa y útil. Las propiedades fundamentales necesarias son solo las ilustradas en Ejemplo para el caso clásico.
Definición
Un sistema de probabilidad consiste en un conjunto básico\(\Omega\) de resultados elementales de un ensayo o experimento, una clase de eventos como subconjuntos del espacio básico y una medida de probabilidad\(P(\cdot)\) que asigna valores a los eventos de acuerdo con las siguientes reglas
(P1): Para cualquier evento\(A\), la probabilidad\(P(A) \ge 0\).
(P2): La probabilidad del evento seguro\(P(\Omega) = 1\).
(P3): Aditividad contable. Si\({A_i : 1 \in J}\) es una clase de eventos mutuamente excluyentes y contables, entonces la probabilidad de la unión disjunta es la suma de las probabilidades individuales.
La necesidad de la exclusividad mutua (desjointedness) se ilustra en Ejemplo. Si los conjuntos no fueran disjuntos, la probabilidad se contaría más de una vez en la suma. Una probabilidad, como se define, es abstracta, simplemente un número asignado a cada conjunto que representa un evento. Pero podemos darle una interpretación que ayude a visualizar los diversos patrones y relaciones encontradas. Podemos pensar en la probabilidad como masa asignada a un evento. La masa unitaria total se asigna al conjunto básico\(\Omega\). La propiedad de aditividad para conjuntos disjuntos hace que la interpretación de masas sea consistente. Podemos utilizar esta interpretación como una representación precisa. En repetidas ocasiones nos referimos a la masa de probabilidad asignada a un conjunto dado. La masa es proporcional al peso, por lo que a veces hablamos informalmente del peso más que de la masa. Ahora una asignación masiva con tres propiedades no parece un comienzo muy prometedor. Pero pronto ampliamos esta rudimentaria lista de propiedades. Utilizamos la interpretación masiva para ayudar a visualizar las propiedades, pero nos preocupa principalmente interpretarlas en términos de probabilidades.
(P4):\(P(A^c) = 1 - P(A)\). Lo que se desprende de la aditividad y el hecho de que
\(1 = P(\Omega) = P(A \bigvee A^c) = P(A) + P(A^c)\)
(P5):\(P(\emptyset) = 0\). El conjunto vacío representa un evento imposible. No tiene miembros, por lo tanto no puede ocurrir. Parece razonable que se le asigne probabilidad cero (masa). Ya que\(\emptyset = \Omega^c\), esto se desprende lógicamente de P (4) y (P2).
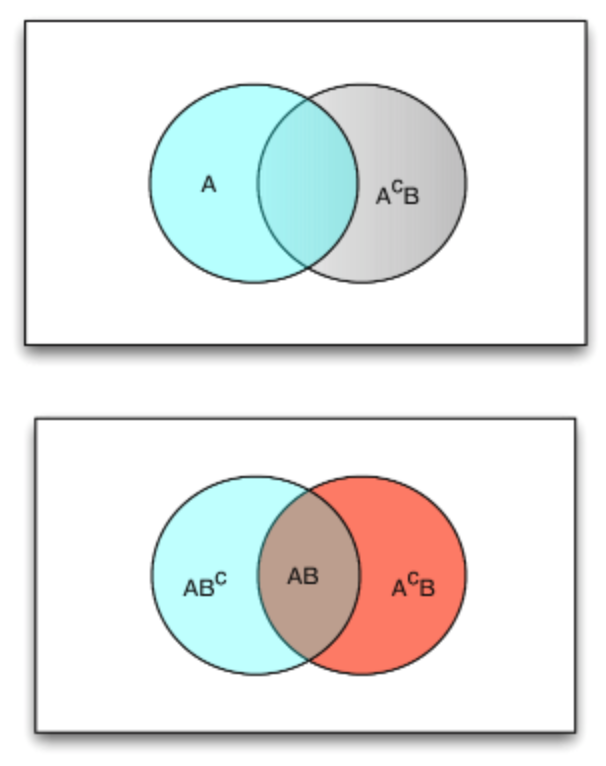
Figura 1.2.1: Particiones de la unión\(A \cup B\)
(P6): Si\(A \subset B\), entonces\(P(A) \le P(B)\). Desde el punto de vista de la masa, cada punto en también\(A\) está\(B\) adentro, por lo que\(B\) debe tener al menos tanta masa como\(A\). Ahora la relación\(A \subset B\) significa que si\(A\) ocurre, también\(B\) debe. De ahí\(B\) que al menos sea tan probable que ocurra como\(A\). Desde un punto de vista puramente formal, tenemos
\(B = A \bigvee A^c B\)de manera que\(P(B) = P(A) + P(A^c B) \ge P(A)\) desde\(P(A^c B) \ge 0\)
(P7):\(P(A \cup B) = P(A) + P(A^c B) = P(B) + P(AB^c) = P(AB^c) + P(AB) + P(A^cB)\)
\(= P(A) + P(B) - P(AB)\)
Las tres primeras expresiones se derivan de la aditividad y la partición de la\(A \cup B\) siguiente manera (ver Figura 1.2.1).
\(A \cup B = A \bigvee A^c B = B \bigvee AB^c = AB^c \bigvee AB \bigvee A^c B\)
Si sumamos las dos primeras expresiones y restamos la tercera, obtenemos la última expresión. En términos de masa de probabilidad, la primera expresión dice que la probabilidad en\(A \cup B\) es la masa de probabilidad in\(A\) más la masa de probabilidad adicional en la parte de la\(B\) cual no está en\(A\). Una interpretación similar se sostiene para la segunda expresión. El tercero es la probabilidad en la parte común más el extra in\(A\) y el extra in\(B\). Si agregamos la masa\(A\) y\(B\) hemos contado la masa en la parte común dos veces. La última expresión muestra que corrigimos esto quitando la masa extra común.
(P8): Si\({B_i : i \in J}\) es una clase contable, disjunta y\(A\) está contenida en la unión, entonces
\(A = \bigvee_{i \in J} AB_i\)para que\(P(A) = \sum_{i \in J} P(AB_i)\)
(P9): Subaditividad. Si\(A = \bigcup_{i = 1}^{\infty} A_i\), entonces\(P(A) \le \sum_{i = 1}^{\infty} P(A_i)\). Esto se desprende de la aditividad contable, la propiedad (P6) y el hecho
(Particiones)
\(A = \bigcup_{i = 1}^{\infty} A_i = \bigvee_{i = 1}^{\infty} B_i\), donde\(B_i = A_i A_1^c A_2^c \cdot\cdot\cdot A_{i - 1}^c \subset A_i\)
Esto incluye como caso especial la unión de un número finito de eventos.
Algunas de estas propiedades, como (P4), (P5) y (P6), son tan elementales que parece que deberían incluirse en la declaración definitoria. Esto no sería incorrecto, pero sería ineficiente. Si tenemos una asignación de números a los eventos, solo necesitamos establecer (P1), (P2) y (P3) para poder afirmar que la asignación constituye una medida de probabilidad. Y las otras propiedades siguen como consecuencias lógicas.
Flexibilidad a un precio
Al ir más allá del modelo clásico, hemos ganado una gran flexibilidad y adaptabilidad del modelo. Se puede utilizar para sistemas en los que el número de resultados es infinito (contable o incontables). No requiere una distribución uniforme de la masa de probabilidad entre los resultados. Por ejemplo, el problema de los dados puede manejarse directamente asignando las probabilidades apropiadas a los diversos números de puntos totales, del 2 al 12. Como vemos en el tratamiento de la probabilidad condicional, hacemos nuevas asignaciones de probabilidad (es decir, introducir nuevas medidas de probabilidad) cuando se obtiene información parcial sobre el resultado.
Pero esta libertad se obtiene a un precio. En el caso clásico, el valor de probabilidad de que se le asigne un evento está claramente definido (aunque puede ser muy difícil realizar el conteo requerido). En el caso general, debemos recurrir a la experiencia, estructura del sistema estudiado, experimento, o estudios estadísticos para asignar probabilidades.
La existencia de incertidumbre por “azar” o “aleatoriedad” no implica necesariamente que el acto de realizar el ensayo sea fortuito. El ensayo puede ser planificado con bastante cuidado; la contingencia puede ser el resultado de factores ajenos al control o conocimiento del experimentador. El mecanismo del azar (es decir, la fuente de la incertidumbre) puede depender de la naturaleza del proceso o sistema real observado. Por ejemplo, al tomar un perfil de temperatura horaria en un día determinado en una estación meteorológica, las principales variaciones no se deben a un error experimental sino a factores desconocidos que convergen para proporcionar el patrón meteorológico específico experimentado. En el caso de un error de transmisión digital no corregido, la causa de la incertidumbre radica en las complejidades de los mecanismos de corrección y las perturbaciones producidas por un entorno muy complejo. Un paciente en una clínica puede ser autoseleccionado. Antes de su aparición y el resultado de una prueba, el médico puede no saber qué paciente con qué condición aparecerá. En cada caso, desde el punto de vista del experimentador, la causa simplemente se atribuye al “azar”. Ya sea que uno vea esto como un “acto de los dioses” o simplemente el resultado de una configuración de causas físicas o conductuales demasiado complejas de analizar, la situación es de incertidumbre, antes del juicio, sobre qué resultado se presentará.
Si hubiera total incertidumbre, la situación sería caótica. Pero este no suele ser el caso. Si bien existe un número extremadamente grande de posibles perfiles de temperatura por hora, un subconjunto sustancial de estos tiene muy poca probabilidad de ocurrir. Por ejemplo, los perfiles en los que las sucesivas temperaturas horarias se alternan entre valores muy altos y luego muy bajos a lo largo del día constituyen un subconjunto poco probable (evento). Normalmente se esperan tendencias en las temperaturas durante el periodo de 24 horas. Si bien un ingeniero de tránsito no sabe exactamente cuántos vehículos se observarán en un período de tiempo determinado, la experiencia brinda alguna idea de qué rango de valores esperar. Si bien existe incertidumbre sobre qué paciente, con qué síntomas, aparecerá en una clínica, un médico ciertamente sabe aproximadamente qué fracción de los pacientes de la clínica tiene la enfermedad en cuestión. En un juego de azar, analizado en resultados “igualmente probables”, la suposición de igual verosimilitud se basa en el conocimiento de las simetrías y regularidades estructurales en el mecanismo por el cual se lleva a cabo el juego. Y el número de resultados asociados a un evento dado es conocido, o puede ser determinado.
En cada caso, existe cierta base en los datos estadísticos sobre experiencias pasadas o conocimientos de estructura, regularidad y simetría en el sistema bajo observación que permite asignar probabilidades a la ocurrencia de diversos eventos. Es esta capacidad de asignar probabilidades a los diversos eventos lo que caracteriza la probabilidad aplicada. Sin embargo determinado, la probabilidad es un número asignado a eventos para indicar su probabilidad de ocurrencia. Las asignaciones deben ser consistentes con las propiedades definitorias (P1), (P2), (P3) junto con las propiedades derivadas (P4) a (P9) (más otras que también pueden derivarse de estas). Dado que las probabilidades no están “incorporadas”, como en el caso clásico, un papel primordial de la teoría de la probabilidad es derivar otras probabilidades a partir de un conjunto de probabilitas dadas.


