8.1.1: Láminas retardadoras

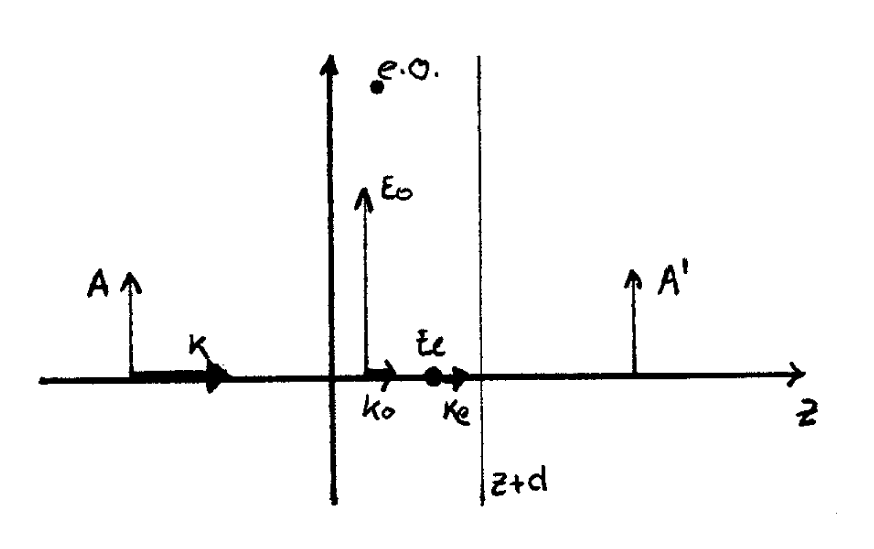
El propósito de estos dispositivos es cambiar la diferencia de fase entre dos ondas. Ya que en los medios anisótropos las dos ondas van a distinta velocidad, se producen desfases de una onda respecto a la otra. Una lámina retardadora puede ser una lámina planoparalela de un medio uniáxico. Para ver lo que pasa sólo tenemos que caracterizar la propagación y relacionar las amplitudes complejas de la onda incidente y de la emergente. Con el sistema de referencia de la figura 8.1 se cumple

\[
k_{x}=k_{y}=0 \notag
\]

Los dos posibles vectores de onda son

\[
\begin{aligned}
\mathbf{k}_{o} &=n_{o} \frac{\omega}{c} \mathbf{u}_{z} \\
\mathbf{k}_{e} &=n_{e} \frac{\omega}{c} \mathbf{u}_{z}
\end{aligned}
\]

(si es \(\perp\) al e.o.). Ambos vectores de onda están sobre el eje \(z\). El campo eléctrico de la ordinaria vibra en el plano del papel (eje \(x\) ) y el de la extraordinaria ortogonal a éste \((y)\).

Para no tener que acudir a las fórmulas de FRESNEL, nos apoyamos en que el medio es transparente y los coeficientes de transmisión deben ser, por analogía al caso isótropo, próximos a 1. Con esta aproximación,

Figure \(\PageIndex{1}\): Lámina planoparalela de anchura \(d\). El eje óptico es perpendicular al plano del papel. La incidencia es normal, según el eje \(z\). - la onda ordinaria estará excitada sólo por la componente \(x\) de la onda incidente

\[
E_{x}(z+d)=A_{x} e^{i\left(k_{o}(z+d)-\omega t\right)}=e^{i k_{o} d} E_{x}(z) \notag
\]

• la componente \(y\) excita la onda extraordinaria

\[
E_{y}(z+d)=A_{y} e^{i\left(k_{e}(z+d)-\omega t\right)}=e^{i k_{e} d} E_{y}(z) \notag
\]

Esa misma relación, en términos de amplitudes es

\[
\begin{aligned}
&A_{x}^{\prime}=e^{i k_{o} d} A_{x} \\
&A_{y}^{\prime}=e^{i k_{e} d} A_{y}
\end{aligned}
\]

el cambio de fase es distinto para cada componente, en virtud de la anisotropía \(\left(k_{e} \neq k_{o}\right)\). A efectos de polarización podemos escribir las relaciones anteriores como

\[
\begin{aligned}
A_{x}^{\prime} &=A_{x} \\
A_{y}^{\prime} &=e^{-i \delta} A_{y}
\end{aligned}
\]

donde \(\delta\) es la diferencia de fases entre las componentes de la onda emergente.

\[
\delta=\left(k_{o}-k_{e}\right) d=\frac{\omega}{c}\left(n_{o}-n_{e}\right) d=\frac{2 \pi}{\lambda}\left(n_{o}-n_{e}\right) d \notag
\]

y \(\lambda\) es la longitud de onda en el vacío. Una escritura matricial es

\[
\left(\begin{array}{c}
A_{x}^{\prime} \notag \\
A_{y}^{\prime}
\end{array}\right)=\left(\begin{array}{cc}
1 & 0 \notag \\
0 & e^{-i \delta}
\end{array}\right)\left(\begin{array}{c}
A_{x} \notag \\
A_{y}
\end{array}\right) \notag
\]

la matriz se llama matriz de Jones de la lámina retardadora. En este caso está escrita en la base en la que \(y\) es el eje óptico. Si queremos expresarla para una base en la que el eje óptico forma un ángulo \(\alpha\) con el eje \(y\) sólo hay que aplicar una rotación a la matriz que tenemos 1 :

\[
\begin{aligned}
\mathrm{M} &=\mathrm{R}_{\alpha}^{-1}\left(\begin{array}{cc}
1 & 0 \\
0 & e^{-i \delta}
\end{array}\right) \mathrm{R}_{\alpha} \\
&=\left(\begin{array}{cc}
\cos ^{2} \alpha+e^{-i \delta} \sin ^{2} \alpha & \cos \alpha \sin \alpha\left(1-e^{-i \delta}\right) \\
\cos \alpha \sin \alpha\left(1-e^{-i \delta}\right) & \sin ^{2} \alpha+e^{-i \delta} \cos ^{2} \alpha
\end{array}\right)
\end{aligned}
\]

Los ejes en los que la matriz de JONES es más simple se llaman ejes de la lámina.

Comentarios:

• La lámina cambia estados de polarización cambiando la fase relativa entre las dos componentes del campo. Es una forma cómoda y sencilla de hacerlo, porque la luz ni siquiera se desvía.
• El desfase introducido depende del grosor de la lámina.
• El desfase introducido depende de la longitud de onda incidente.
• Si el campo eléctrico vibra en la dirección del eje óptico, luz lineal se convertiría en luz lineal. Es decir, si la luz vibra según uno de los ejes de la lámina, la lámina no cambia su estado de polarización, porque no hay dos componentes que desfasar.

Las láminas de espesor variable se llaman compensadores y son muy útiles. Las láminas de espesor fijo son específicas de una longitud de onda.

Ejemplo Lámina cuarto de onda

Dentro de las láminas de espesor fijo \({ }^{2}\), vamos a estudiar la lámina cuarto de onda (o \(\frac{\lambda}{4}\) ), que es aquella que introduce un desfase múltiplo impar de \(\frac{\pi}{2}\).

\[
\delta=(2 m+1) \frac{\pi}{2} \notag
\]

con \(m \in \mathcal{Z}\). Para ello

\[
d=\frac{2 m+1}{n_{o}-n_{e}} \dfrac{\lambda}{4} \notag
\]

en sus ejes,

\[
\mathrm{M}=\left(\begin{array}{cc}
1 & 0 \notag \\
0 & \pm i
\end{array}\right) \notag
\]

Una aplicación es convertir luz linealmente polarizada en elípticamente polarizada, pero con la particularidad de que los ejes de la elipse de luz emergente coinciden con los ejes de la lámina.

\[
\begin{array}{r}
\text { lineal } \leftrightarrow \quad \text { elíptica } \notag \\
\left(\begin{array}{c}
\cos \theta \notag \\
\sin \theta
\end{array}\right) \rightarrow\left[\frac{\lambda}{4}\right] \rightarrow\left(\begin{array}{c}
\cos \theta \notag \\
\pm i \sin \theta
\end{array}\right)
\end{array} \notag
\]

De este modo, sabemos cómo está orientada la elipse. Si \(\theta\) de la luz lineal es \(\frac{\pi}{4}\) tendríamos luz emergente circularmente polarizada.

_{__________________________________________________________}

^{1. Si al hacer los cálculos encuentras discrepancias de signos, seguramente se deben a una elección distinta del referencial de ángulos.}