10.8.1: Análisis del factor de interferencia

Última actualización
Guardar como PDF

Page ID: 51210

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Es precisamente este factor, tan diferente de \((1+\cos \varphi)\), el que permitirá usar la red de difracción para discriminar longitudes con gran precisión. Al depender en el numerador de un seno es sencillo encontrar los ceros de la función: son los del numerador, que son \((m \in \mathcal{Z})\)

\[
\begin{aligned}
N \frac{\varphi}{2} &=m \pi \\
\varphi &=\frac{2 m}{N} \pi
\end{aligned}
\]

esto es cierto para todos los valores de \(\varphi\) salvo para los valores en que se anule también el denominador, que vamos a numerar con \(M\)

\[
\varphi=2 M \pi \notag
\]

Los ceros comunes corresponden a los valores máximos más grandes, y aparecen en \(\varphi=0, \pm 2 \pi, \pm 4 \pi, \ldots\)

El aspecto de la función es el que se muestra en la figura. Para justificar el que los 10 Difracción

Figura \(\PageIndex{1}\): Red de difracción. La ecuación \(\varphi=2 \pi M\) da la ubicación de los máximos principales. La figura es para \(N=10\), escogiendo \(\phi=4 \varphi\).

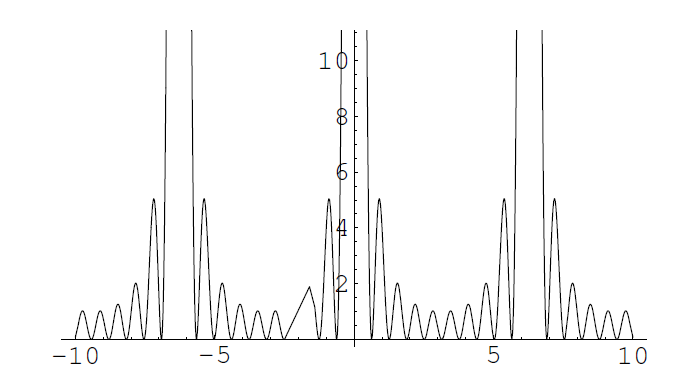
máximos principales realmente lo son valgan los siguientes cálculos

\[
\begin{aligned}
\lim _{\varphi \rightarrow 0} I_{d} &=\lim _{\varphi \rightarrow 0} \text { cte }\left(\frac{\sin \left(N \frac{\varphi}{2}\right)}{\sin \frac{\varphi}{2}}\right) \\
&=\operatorname{cte}\left(\frac{N \varphi / 2}{\varphi / 2}\right) \\
&=\text { cte } \times N^{2}
\end{aligned}
\]

Tenemos que comparar con los máximos secundarios. Cuando \(N\) es muy grande \((N \gg 1)\), que es el caso interesante

\[
\begin{aligned}
I_{d} &=\operatorname{cte}\left(\frac{\sin \left(N \frac{3 \pi}{2 N}\right)}{\sin \left(\frac{3 \pi}{2 N}\right)}\right)^{2} \\
& \simeq \text { cte } \times \frac{1}{\left(\frac{3 \pi}{2 N}\right)^{2}} \\
& \simeq \text { cte } \times \frac{N^{2}}{25}
\end{aligned}
\]

de modo que la altura relativa de los máximos, cuando \(N\) es muy grande, difiere por un factor de 25 entre los principales y los adyacentes a éstos.