10.8.2: Modulación de la interferencia por la difracción
- Page ID
- 51211
Los máximos principales ya no tienen todos la misma altura. El máximo principal es para
\[
\begin{aligned}
\varphi &=\phi=0 \\
x^{\prime} &=f^{\prime} \sin \theta \\
\theta^{\prime} &=\theta
\end{aligned}
\]
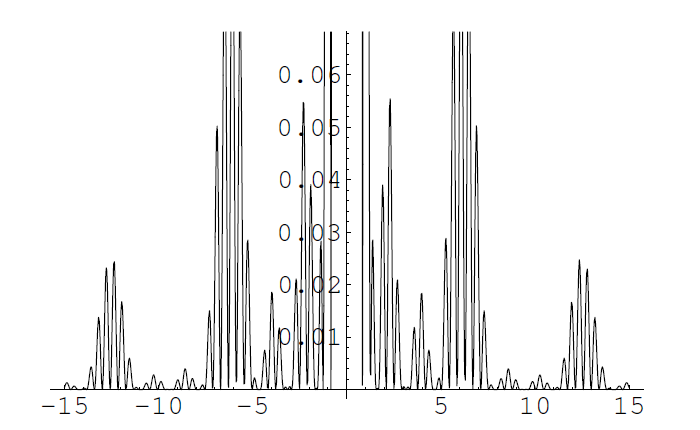
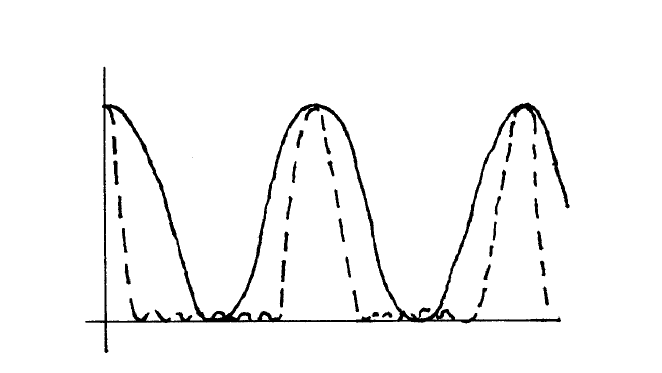
Si queremos ver varios máximos de interferencia tendremos que reducir las rendijas para que la envolvente de difracción se haga más suave. Los máximos se encuentran en la dirección de incidencia, \(\theta\).
Poder resolutivo
Hay que señalar que los máximos de la doble rendija y los máximos de la red de difracción coinciden. Podemos ver en la figura \(10.26\) que añadir más rendijas se traduce en que los máximos se contraen (son cada vez más estrechos: su anchura es proporcional a \(\frac{1}{N}\) ). El interferómetro de FP estaba caracterizado por la estrechez de los máximos, y era esto lo que permitía medir magnitudes. La red de difracción es a estos efectos tanto más sensible cuanto más grande sea el número de rendijas.
Vamos a construir un parámetro que nos permita evaluar la precisión en la medida de longitudes de onda de este dispositivo.
Un criterio posible es considerar que los máximos están resueltos si la distancia de los máximos es mayor que la mitad de su anchura
\[
|\Delta \varphi| \geq \frac{\delta \varphi}{2} \notag
\]
en términos de los datos del problema
\[
\begin{aligned}
|\Delta \varphi| & \geq \frac{2 \pi}{N} \\
|\Delta \varphi| &=\frac{2 \pi}{\lambda^{2}}\left(\sin \theta^{\prime}-\sin \theta\right) d \Delta \lambda \\
\varphi &=\frac{2 \pi}{\lambda}\left(\sin \theta^{\prime}-\sin \theta\right) d=2 \pi M
\end{aligned}
\]
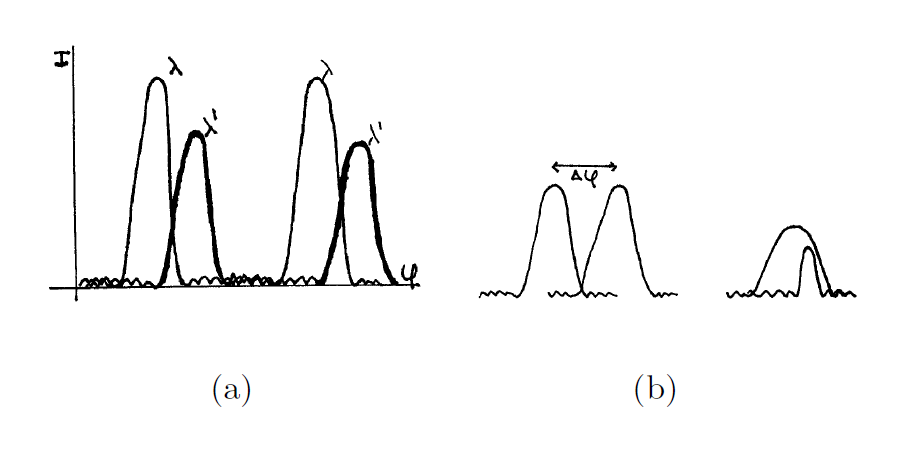
como
\[
2 \pi|M| \frac{\Delta \lambda}{\lambda} \geq \frac{2 \pi}{N} \notag
\]
se tiene el criterio
\[
\frac{\Delta \lambda}{\lambda} \geq \frac{1}{|M| N} \notag
\]
o, más habitualmente
\[
\frac{\lambda}{\Delta \lambda} \leq|M| N \notag
\]
Comentario: el poder resolutivo depende de dos factores. Hay un factor que depende del interferómetro \((N)\) y otro de cómo lo utilicemos (orden de interferencia \(M\) ). Conseguir órdenes grandes es difícil por comparación al FABRY-PEROT.
Ejemplo Número de rendijas para resolver el doblete amarillo del sodio \((\lambda=589.0 \mathrm{~nm}\) y \(\lambda^{\prime}=589.6 n m\) ) cuando la anchura de la red es de \(10 \mathrm{~cm}\) y \(M=1\). Calcular la separación \(d\) de las rendijas.
Como \(\lambda\) podemos tomar una cualquiera de ellas o el valor medio. \(\Delta \lambda=0.6 n m\). En el orden 1 tenemos \(N \geq \frac{\lambda}{\Delta \lambda} \simeq 982\). En cuanto a \(d\)
\[
d \simeq \frac{10 \mathrm{~cm}}{1000}=10^{-4} \mathrm{~m} \notag
\]
deben estar a décimas de milímetro de distancia. Tomar una placa más grande no es solución, porque si se pierde la coherencia espacial no hay interferencia.

