1.4: Direcciones y Notación
- Page ID
- 126767
La fuerza de un haz de radiación paralelo plano se especifica por la densidad de flujo radiante F vatios por metro cuadrado tal que F = dP/dA, donde A es el área perpendicular a la dirección de propagación. Por lo tanto, F es igual al flujo neto π F utilizado por Chandrasekhar, con la importante excepción de que F se usa solo para un haz plano paralelo.
Dado que la ecuación de transferencia trata solo en radiancias, ahora abordaremos la pregunta bastante intrigante: “¿Cuál es el resplandor de un haz plano paralelo?”
La Figura 2 muestra un rayo de un haz plano paralelo de densidad de flujo F incidente sobre la superficie de un medio de dispersión. Dejaremos que el resplandor incidente resultante sea L i, el cual, usando la notación de Chandrasekhar se especificaría en posición y dirección como
\[L_{i}=L\left(0,-\mu_{0}, \varphi_{0}\right), \quad \mu_{0}=\left|\cos \vartheta_{0}\right|\]
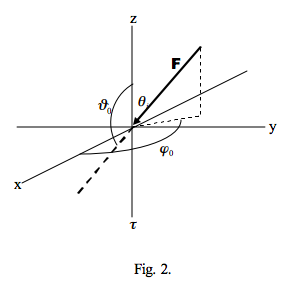
Muchos autores especifican la dirección polar de esta radiación en términos de un ángulo de incidencia, digamos i o θ i, como el ángulo entre la superficie normal y el rayo incidente, de tal manera que i = π -\( \vartheta_0\) y definen μ 0 como μ 0 = cos i.
La distribución angular de F (o, más bien, su falta de ella) puede especificarse analíticamente haciendo uso de la función delta de Dirac, que tiene la propiedad de que
\(\int_{-\infty}^{\infty} f(x) \delta(x-a) d x=f(a)\)
y, quizás lo más importante, para cualquier ε > 0
\(\int_{a-\varepsilon}^{a+\varepsilon} f(x) \delta(x-a) d x=f(a).\)
El resplandor incidente en la superficie en la dirección (-μ 0, φ 0) es entonces 1
\[L_{i}=\mathbf{F} \delta\left(\mu-\mu_{0}\right) \delta\left(\varphi-\varphi_{0}\right)\]
La Figura 3 muestra un haz reflejado de resplandor Lr donde
\[L_{r}=L(0,+\mu, \varphi), \quad \mu=\cos \vartheta\]
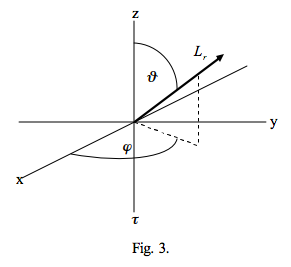
Nuevamente, muchos autores definen la dirección polar de reflexión en términos de un ángulo de reflexión, el ángulo entre la superficie normal y el rayo reflejado, digamos θ r (que es lo mismo que\(\vartheta\)), y definen μ como cos θ r.
La figura 4 muestra un rayo de radiancia transmitido Lt donde
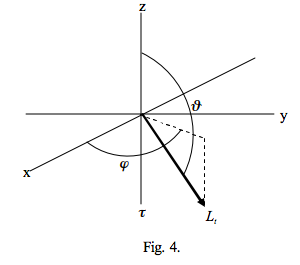
Surge entonces la pregunta: ¿son siempre positivos los valores de μ 0 y μ, introducidos por Chandrasekhar y retomados por otros, aunque con definiciones diferentes? La respuesta a esto es, en su mayoría, sí, pero hay que tener cuidado dependiendo del contexto en el que ocurran, como, por ejemplo, en los siguientes casos.
Considerar el problema de determinar el ángulo de fase 0 ≤ α ≤ π entre las direcciones incidente y reflejada o transmitida μ 0 y μ, donde
\[\cos \alpha=\mu_{0} \mu+\sqrt{\left(1-\mu_{0}^{2}\right)\left(1-\mu^{2}\right)} \cos \left(\varphi-\varphi_{0}\right).\]
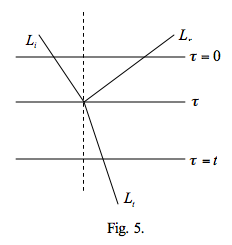
Para la reflexión tanto m como m0 son positivos, pero para los rayos transmitidos m debe ser negativo. La función de fase p a menudo se expresa en términos de a o cos a. O, considere, como en la figura 5, las longitudes de trayectoria óptica de la radiación reflejada y transmitida desde una profundidad dentro de un medio de espesor óptico t. La trayectoria óptica total para el rayo reflejado es τ/μ 0 + τ/μ r y para el rayo transmitido τ/μ 0 + (t - τ) /μ t en el que μ 0, μ r y μ t son todos positivos.
1 Si la ecuación (7) te molesta en que su lado derecho no parece tener unidades de resplandor, entonces no te preocupes; en el capítulo 2 demostraremos que efectivamente sí tiene tales unidades.


