3.1: Una breve historia de la Ley Lommel-Seeliger
- Page ID
- 126599
Introducción. El uso de la ley Lommel-Seeliger es un aspecto perdurable de la fotometría planetaria. Tiene la ventaja de la simplicidad analítica así como, en muchos casos, de ser una excelente primera aproximación a la reflexión difusa. A pesar de sus deficiencias, en particular su incapacidad para mostrar un efecto de oposición, sigue siendo muy utilizada hoy en día en aplicaciones tan diversas como la inversión de curvas de luz (la determinación de polos y formas de asteroides a partir de sus curvas de luz (Kaasalainen, 2003)), hasta la predicción de firmas fotométricas de planetas extrasolares anillados no resueltos (Arnold & Schneider, 2004). En efecto, es el tema de los exoplanetas el que recientemente ha generado un interés por la fotometría planetaria por parte de astrónomos que de otra manera no estarían preocupados por el tema.
Aquí presentamos la ley Lommel-Seeliger con cierto detalle y como resultado señalamos la existencia y consecuencias de un error insidioso, que se ha filtrado a través de la literatura.
Descripción. La ley de Lommel-Seeliger se basa en un modelo físico simple de reflexión difusa. Como tal se trata de un único modelo de dispersión en el que la dispersión es isotrópica.
El modelo asume que la luz penetra en la superficie, siendo atenuada exponencialmente a medida que lo hace. Aquí la atenuación se refiere a cualquier proceso que reduzca el brillo de un haz de luz, y por lo tanto incluye dispersión y absorción. Cada elemento de volumen que encuentra el haz atenuado dispersa parte de él isotrópicamente, es decir, igualmente en todas las direcciones hacia los\(4π\) esteradianos (la esfera imaginaria, si quieres) que lo rodean. Así, de esta radiación difusa dispersa, solo la mitad se dirige de nuevo hacia la superficie, y esta fracción se atenuará aún más antes de emerger como radiación reflejada difusa.
Derivación. La siguiente derivación pretende ser más ilustrativa que completamente rigurosa y contiene algunos atajos. No obstante, es correcto; para una prueba más robusta y general véase el Capítulo 1.
Considerar, como se muestra en la Figura\(\PageIndex{1}\), una capa difusa reflectante (y transmisora) de espesor óptico normal\(t\), en la que el espesor óptico incluye atenuación tanto por dispersión como por absorción. En problemas de esta naturaleza, es más conveniente trabajar en términos de espesor óptico que grosor físico real. La luz que atraviesa una trayectoria de espesor óptico\(τ\) se atenúa por un factor\(e^{-τ}\).
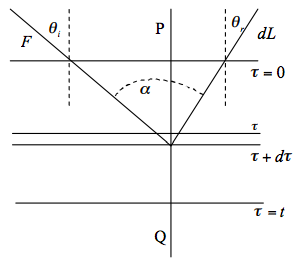
La superficie (τ = 0) es irradiada por un haz plano paralelo de densidad de flujo radiante\(F\) en un ángulo de incidencia\(θ_i\), de manera que la irradiancia es\(E = F \cos θ)i\). Nos preocupa el resplandor resultante en la dirección de un ángulo de reflexión\(θ_r < 90^o\). Ahora vamos\(μ_0 = \cos θ_i\)\(μ = \cos θ_r\) y consideremos la capa entre\(τ\) y\(τ + dτ\). La densidad de flujo incidente que ha penetrado a este nivel es\(Fe^{-τ/μ_0}\).
La contribución al resplandor difuso en la dirección μ por dispersión isotrópica es así\( \dfrac{\varpi_{0}}{4 \pi} F e^{-\tau / \mu_{0}} \dfrac{d \tau}{\mu}\) donde\(ϖ_0\) está el albedo de dispersión única. Esta radiación será atenuada aún más por el factor\(e^{-τ/μ}\) antes de emerger de la superficie, de manera que la contribución a la luminosidad en la dirección\(μ\) es
\[d L=\dfrac{\varpi_{0}}{4 \pi} F e^{-\tau / \mu_{0}} \dfrac{d \tau}{\mu} e^{-\tau / \mu}.\]
Tenga en cuenta que\(dL\) es la contribución al resplandor total de la capa resultante de la dispersión única. El modelo Lommel-Seeliger considera únicamente la dispersión de la luz incidente colimada. No toma en cuenta la dispersión de la luz difusa que se ha abierto paso indirectamente a la misma posición al estar dispersada una o más veces, es decir, no considera dispersión múltiple.
Para una superficie planetaria, la capa es “semi-infinita” (\(t = ∞\)) y el resplandor total en la dirección\(μ\) es
\[L=\dfrac{\varpi_{0} F}{4 \pi \mu} \times \int_{0}^{\infty} \exp \left[-\tau\left(\dfrac{1}{\mu_{0}}+\dfrac{1}{\mu}\right)\right] d \tau.\]
resultando en
\[L=\dfrac{\varpi_{0} F}{4 \pi \mu} \dfrac{\mu_{0} \mu}{\mu+\mu_{0}};\]
y, dado que la irradiancia es\(E = Fμ_0\) y\(L = f_r E\), se deduce que la función de distribución de reflectancia bidireccional (BRDF) que define la regla de reflectancia Lommel-Seeliger es
\[f_{r}=\dfrac{\varpi_{0}}{4 \pi} \dfrac{1}{\mu+\mu_{0}}.\]
El uso del modelo Lommel-Seeliger no se limita a las superficies planetarias. Para una capa de espesor óptico finito t, por ejemplo, un anillo planetario (exo), el resplandor reflejado es
\[L_{R}=\dfrac{\varpi_{0} F}{4 \pi \mu} \times \int_{0}^{t} \exp \left[-\tau\left(\dfrac{1}{\mu_{0}}+\dfrac{1}{\mu}\right)\right] d \tau,\]
resultando en
\[L_{R}=\dfrac{\varpi_{0}}{4 \pi} \dfrac{1}{\mu+\mu_{0}} \times\left[1-\exp \left\{-t\left(\dfrac{1}{\mu_{0}}+\dfrac{1}{\mu}\right)\right\}\right] \mu_{0} F;\]
y por razonamiento similar se puede determinar el resplandor\(L_T\) transmitido a través de la capa (Arnold & Schneider, 2004).
Errores en la literatura. El error más antiguo que el autor ha podido detectar se remonta a 1916 en un artículo sobre albedos planetarios de (nada menos que) Henry Norris Russell (Russell, 1916). En ese trabajo el BRDF se expresa implícitamente como
\[f_{r}=\dfrac{\gamma}{\mu_{0}+\mu}\]
en la que\(γ\) es una constante. De esto Russell deriva la reflectancia hemisférica direccional (albedo hemisférico)
\[\rho\left(\mu_{0}\right)=2 \pi \gamma \quad \times \quad\left[1-\mu_{0} \ln \left(1+1 / \mu_{0}\right)\right],\]
donde puede verse que la expresión entre paréntesis varía monótonamente de 0.308 (μ 0 = 1) a unidad (μ 0 = 0); luego argumenta “Dado que (ρ) nunca puede superar la unidad se deduce que πγ no puede ser mayor 0.5 ni (el albedo Bond) A que 0.409. De ahí que un planeta para el que (el albedo geométrico) p supere 0.25 no pueda reflejar la luz en estricto apego a la ley de Lommel-Seeliger”.
Aunque este argumento suena completamente plausible, está equivocado. Si bien es cierto que\(ρ\), como cualquier albedo, no puede rebasar la unidad, en el caso de la ley Lommel-Seeliger no puede rebasar\( \dfrac{1}{2}\) y por lo tanto el valor máximo de γ\( \dfrac{1}{4 \pi}\) no lo es\( \dfrac{1}{2 \pi}\); el valor de γ lo es\( \dfrac{\varpi_{0}}{4 \pi}\). Tal error puede afectar los cálculos de albedo por un hecho o de dos. Desafortunadamente, este error se ha filtrado en publicaciones posteriores, por ejemplo, Lester, McCall & Tatum (1979), Fairbairn (2002, 2004). Las propiedades correctas de la ley Lommelseeliger se resumen en la Tabla I.
| Propiedades de Superficies | Ley de Reflectancia Lommel-Seeliger | Esferas | |
|---|---|---|---|
| f r | \(\dfrac{\varpi_{0}}{4 \pi} \dfrac{1}{\mu_{0}+\mu}\) | q | \(\dfrac{16}{3}(1-\ln 2)\) |
| ρ (0.5) | \(\dfrac{\varpi_{0}}{2}\left[1-\mu_{0} \ln \left(1+1 / \mu_{0}\right)\right]\) | p (0.125) | \( \dfrac{ \varpi_0}{8}\) |
| p n (0.125) | \( \dfrac{ \varpi_0}{8}\) | A (0.2046) | \(\dfrac{2}{3} \varpi_{0}(1-\ln 2)\) |
Para algunas aplicaciones, el error de un factor de dos no tiene ninguna consecuencia. En los casos en los que solo importan las magnitudes relativas, de manera que el desplazamiento es arbitrario, el factor desaparece en el desplazamiento. Los perfiles de curvas de luz de asteroides son tales ejemplos.
Referencias
Arnold, L. & Schneider, J. 2004, A&A, 420, 1153-1162
Fairbairn, M. B. 2002, JRASC, 96, 18
Fairbairn, M. B. 2004, JRASC, 98, 149
Hapke, B. 1981, J. Geophys. Res., 86, 3039
Kaasalainen, M. 2003, JRASC, 97, 283
Lester, P.L., McCall, M.L. & Tatum, J.B. 1979, JRASC, 73, 233
Russell, H.N. 1916, ApJ, 43, 173


