6.7: Problemas y soluciones

Ejercicio\(\PageIndex{1}\)

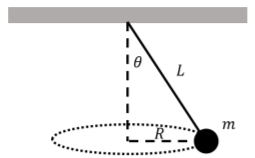
Considera un péndulo cónico con una masa\(m\), attached to a string of length \(L\). The mass executes uniform circular motion in the horizontal plane, about a circle of radius \(R\), as shown in Figure \(\PageIndex{1}\). One can think of the horizontal circle and the point where the string is attached to as forming a cone. The circular motion is such that the (constant) angle between the string and the vertical is \(\theta\).

1. Derivar una expresión para la tensión en la cuerda.
2. Derivar una expresión para la velocidad de la masa.
3. Derivar una expresión para el periodo de la moción.

Figura\(\PageIndex{1}\): El péndulo cónico.

Contestar

a. Comenzamos por identificar las fuerzas que están actuando sobre la masa. Estos son:

• \(\vec F_g\), su peso, con una magnitud\(mg\).
• \(\vec F_T\), una fuerza de tensión ejercida por la cuerda.

Las fuerzas se ilustran en la Figura\(\PageIndex{2}\), junto con nuestra elección del sistema de coordenadas y la dirección de la aceleración de la masa (hacia el centro del círculo).

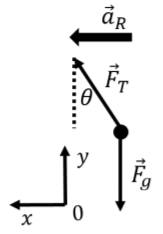
Figura\(\PageIndex{2}\): Fuerzas que actúan sobre el péndulo cónico.

El\(y\) componente de la Segunda ley de Newton da la relación entre la tensión en la cuerda, el peso y el ángulo\(\theta\)\[\begin{aligned} \sum F_y&=0 \\ F_T\cos\theta -F_g&=0 \\ F_T\cos\theta&=mg \\ \therefore F_T&=\frac{mg}{\cos\theta} \\\end{aligned}\]

b. para que la masa se mueva en círculo, la fuerza neta debe dirigirse en todo momento hacia el centro del círculo. El\(x\) componente de la Segunda Ley de Newton, combinado con nuestra expresión para la magnitud de la tensión\(F_T\), nos permite determinar la velocidad de la masa:\[\begin{aligned} \sum F_x&=ma_r \\ F_T\sin\theta&=m\frac{v^2}{R}\\ \left(\frac{mg}{\cos\theta}\right)\sin\theta &=m\frac{v^2}{R}\\ g\tan\theta&=\frac{v^2}{R}\\ \therefore v &= \sqrt{gR\tan\theta}\end{aligned}\]

c. Ahora que conocemos la velocidad, podemos encontrar fácilmente el periodo,\(T\), del movimiento:\[\begin{aligned} T&=\frac{2\pi R}{v} \\ &=\frac{2\pi R}{\sqrt{gR\tan\theta }}=2\pi\sqrt{\frac{R}{g\tan\theta}}\end{aligned}\]

Ejercicio\(\PageIndex{2}\)

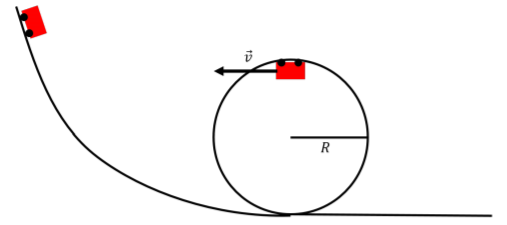
Barb y Kenny van al parque de diversiones. Barb insiste en montar la montaña rusa gigante, pero Kenny tiene miedo de que se caigan de la montaña rusa en lo alto del bucle. Barb tranquiliza a Kenny al pedirle más información al técnico de montaña rusa. El técnico dice que viajarán a\(15\text{m/s}\) when upside down, and that the roller coaster loop has a radius of \(22\text{m}\). Kenny is still skeptical. Is he correct in being skeptical?

Figura\(\PageIndex{3}\): La montaña rusa

Contestar

Tenemos que determinar si la velocidad de Barb y Kenny es lo suficientemente grande como para que den la vuelta al círculo. La velocidad mínima que deben tener en la parte superior del bucle es tal que su peso (la única fuerza que actúa sobre ellos) proporciona la fuerza centrípeta (neta) requerida para rodear el bucle.

Escribiendo la Segunda Ley de Newton en la dirección vertical, para el caso donde solo el peso actúa sobre Barb o Kenny (masa\(m\)), cuando van a velocidad\(v\)\[\begin{aligned} mg &= ma_R = m\frac{v^2}{R}\\ \therefore v &= \sqrt{gR} = \sqrt{(9.8\text{m/s}^{2})(22\text{m})}=14.68\text{m/s}\end{aligned}\] Esto corresponde a la velocidad mínima que deben tener en la parte superior del bucle para hacerla alrededor. Si van más rápido, la fuerza normal desde su asiento (hacia abajo, ya que están al revés), resultaría en una fuerza neta mayor hacia el centro del círculo. Esta situación corresponde a la fuerza normal desde su asiento apenas llegando a 0 en la parte superior del bucle. Dado que la montaña rusa se cita por tener una velocidad de\(15\text{m/s}\) en la parte superior del bucle, apenas lo lograrán. Sin embargo, esto está demasiado cerca de la velocidad mínima para no caerse de la montaña rusa, ¡así que Kenny tiene razón al ser escéptico! ¡Los ingenieros que diseñan la montaña rusa deberían incluir un margen de seguridad mucho mayor!