16.7: Problemas y soluciones de la muestra

Última actualización
Guardar como PDF

Page ID: 128952

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ejercicio\(\PageIndex{1}\)

Considera tres varillas cargadas de longitud las\(L\) cuales están dispuestas para formar un triángulo, como se muestra en la Figura\(\PageIndex{1}\). Si la carga en cada varilla se distribuye uniformemente, ¿cuál es el campo eléctrico neto en el centro del triángulo?

Figura\(\PageIndex{1}\): Un triángulo formado por varillas cargadas.

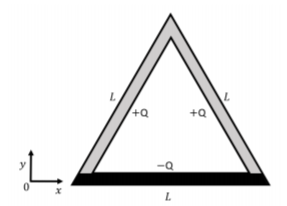
Contestar

Podemos modelar el objeto como la suma de tres cables de longitud finita de la longitud,\(L\). En el Ejemplo 16.3.3, determinamos que el campo eléctrico producido por un cable finito es:\[\begin{aligned} E = \frac{2k\lambda}{R}\sin\theta_0\end{aligned}\] Podemos determinar geométricamente que\(\theta_0 = \frac{\pi}{6}\), como en la Figura\(\PageIndex{2}\). La distancia,\(R\):\[\begin{aligned} R = \frac{L}{2}\sin{\theta_0}\end{aligned}\]

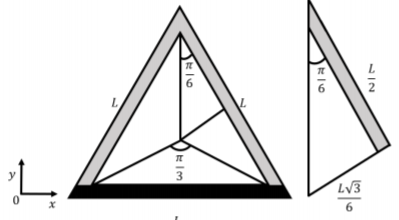
Así, el campo de un cable viene dado por:\[\begin{aligned} E&= \frac{2k\lambda}{R}\sin(\frac{\pi}{6})\\ E &= \frac{k\lambda}{R}\end{aligned}\] Dado que la carga\(Q\) se distribuye uniformemente a lo largo de la varilla de longitud\(L\), podemos reescribir la densidad de carga como\(\frac{Q}{L}\), lo que da:\[\begin{aligned} E &= \frac{k Q}{RL} = \frac{k Q}{\frac{L\sqrt{3}}{6}L} = \frac{6k Q}{\sqrt{3}L^2}\end{aligned}\] Esta es la magnitud del campo eléctrico para cada lado del triángulo. Los dos cables positivos producirán campos eléctricos cuyos componentes verticales cancelan. El cable negativo producirá un campo que apunta hacia abajo. Sumando los vectores del campo eléctrico:\[\begin{aligned} \sum \vec E &= \frac{6k Q}{\sqrt{3}L^2}\left(\cos\left({\frac{\pi}{6}}\right) - \cos\left({\frac{\pi}{6}}\right)\right)\hat{x} + \frac{6k Q}{\sqrt{3}L^2}\left(-1-2\sin\left({\frac{\pi}{6}}\right)\right)\hat y\\ \sum \vec E & = -\frac{12k Q}{\sqrt{3}L^2}\hat y\end{aligned}\] Cuál es la respuesta final.

Ejercicio\(\PageIndex{2}\)

Supongamos que un dipolo está en un campo eléctrico\(\vec E\). Mostrar que el dipolo experimentará un movimiento armónico simple si el ángulo entre el vector dipolo y el vector de campo eléctrico es pequeño.

Contestar: El único par neto en el dipolo es de la fuerza del campo eléctrico:\[\begin{aligned} \tau = -pE\sin\theta \end{aligned}\] donde hemos insertado un signo menos para indicar que se trata de un par restaurador, en la dirección opuesta al ángulo creciente\(\theta\). El par neto es igual al momento de inercia multiplicado por la aceleración angular:\[\begin{aligned} -pE\sin\theta &= I\alpha\\ \therefore \alpha &= -\frac{pE}{I}\sin\theta\sim-\frac{pE}{I}\theta\end{aligned}\] donde en la última igualdad, hicimos la aproximación de ángulo pequeño (\(\sin\theta\sim\theta\)). Esto tiene la forma de movimiento armónico simple:\[\begin{aligned} \frac{d^2\theta}{dt^2}&=-\omega^2 \theta\\ \omega &=\sqrt{\frac{pE}{I}}\end{aligned}\]