3.3: Uso del cálculo para describir el movimiento

Los objetos no necesariamente tienen una velocidad o aceleración constante. Por lo tanto, necesitamos extender nuestra descripción de la posición y velocidad de un objeto a un caso más general. Esto se puede hacer de la misma manera que introdujimos el movimiento acelerado; es decir, pretendiendo que durante un intervalo de tiempo muy pequeño\(∆t\), la velocidad y la aceleración son constantes, y luego considerando el movimiento como la suma a lo largo de muchos intervalos pequeños en el tiempo. En el límite que\(∆t\) tiende a cero, esta será una descripción precisa.

Velocidad instantánea y media

Supongamos que un objeto se mueve con una velocidad no constante, y cubre una distancia\(\Delta x\) en una cantidad de tiempo\(\Delta t\). Podemos definir una velocidad promedio,\(v^{avg}\):

\[v^{avg}= \frac{\Delta x}{\Delta t}\]

Es decir, independientemente de nuestra elección de intervalo de tiempo\(\Delta t\),, siempre podemos calcular la velocidad media,\(v^{avg}\), de un objeto sobre una distancia particular. Esa velocidad promedio será un promedio a lo largo del intervalo, entre algún tiempo\(t\) y\(t+\Delta t\). Si reducimos la longitud del intervalo de tiempo utilizado para medir la velocidad, y tomamos el límite\(\Delta t\rightarrow 0\), podemos definir la velocidad instantánea:

\[v = \lim_{\Delta t\to 0} \frac{\Delta x}{\Delta t}\]

La velocidad instantánea es la velocidad sólo en ese pequeño instante en el tiempo donde elegimos\(\Delta x\) y\(\Delta t\). Otra forma de leer esta ecuación es que la velocidad,\(v\), es la pendiente de la gráfica de\(x(t)\). Recordemos que la pendiente es la “subida sobre carrera”, es decir, el cambio en\(x\) dividido por el cambio correspondiente en\(t\). De hecho, cuando no teníamos aceleración, la posición en función del tiempo, Ecuación 3.1.1, tenía explícitamente la velocidad como pendiente de una función lineal:

\[x(t) = v_{0x}+v_{x}t\]

Si volvemos a la Figura\(\PageIndex{1}\), donde la velocidad ya no era constante, efectivamente podemos ver que la gráfica de la velocidad versus tiempo (\(v(t)\)) corresponde a la pendiente instantánea de la gráfica de posición versus tiempo (\(x(t)\)). Para\(t<1.02\text{s}\), la pendiente de la\(x(t)\) gráfica es positiva pero decreciente (tal cual\(v(t)\)). At\(t=1.02\text{s}\), la pendiente de\(x(t)\) es instantáneamente\(0\text{m/s}\) (como es la velocidad). Finalmente, para\(t>1.02\text{s}\), la pendiente de\(x(t)\) es negativa y aumentando en magnitud, como es\(v(t)\).

Leibniz y Newton fueron los primeros en desarrollar herramientas matemáticas para hacer frente a cálculos que involucran cantidades que tienden a cero, como tenemos aquí para nuestro intervalo de tiempo\(\Delta t\). Hoy en día, llamamos a ese campo de las matemáticas “cálculo”, y vamos a hacer uso de él aquí. Utilizando el vocabulario del cálculo, más que decir que “la velocidad instantánea es la pendiente de la gráfica de posición versus tiempo en algún momento”, decimos que “la velocidad instantánea es la derivada temporal de la posición en función del tiempo”. También usamos una notación ligeramente diferente para que no tengamos que escribir el límite\(\lim_{\Delta t\to 0}\):

\[ v(t)=\lim_{\Delta t\to 0} \frac{\Delta x}{\Delta t}=\frac{dx}{dt}=\frac{d}{dt} x(t)\]

donde realmente podemos pensar\(dt\) como\(\lim_{\Delta t\to 0}\Delta t\), y\(dx\) como el cambio correspondiente de posición en un intervalo de tiempo infinitesimalmente pequeño\(dt\).

De igual manera, introducimos la aceleración instantánea, como la derivada temporal de\(v(t)\):

\[a_x(t)=\frac{dv}{dt}=\frac{d}{dt}v(t)\]

Pensamientos de Olivia

Al mirar una gráfica de posición versus tiempo, a veces es difícil saber a primera vista si la velocidad del objeto está aumentando o disminuyendo. Esta sección nos da una manera fácil de resolverlo. La velocidad es la pendiente instantánea de la gráfica\(x(t)\), por lo que la velocidad es la “pendiente” de esa gráfica. Simplemente dibuja algunas líneas que sean tangentes a (es decir, solo tocar) la curva, y ver qué sucede a medida que aumenta el tiempo. Si las líneas se ponen más pronunciadas, el objeto se está acelerando. Si se están volviendo más planos, el objeto se está desacelerando.

Figura\(\PageIndex{1}\): Dos gráficas\(x(t)\) que muestran líneas tangentes. Izquierda: el objeto se está acelerando (velocidad positiva, aceleración positiva). Derecha: el objeto se está desacelerando (velocidad positiva, aceleración negativa).

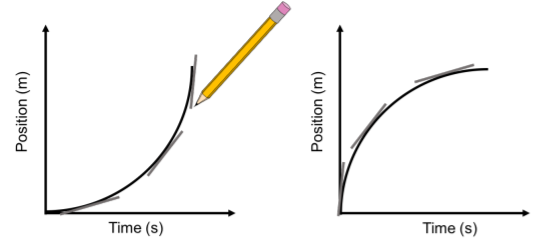
A partir de aquí, también se puede averiguar cuál es la dirección de la aceleración. Si un objeto se está acelerando, la aceleración y la velocidad deben estar en la misma dirección (es decir, ambas positivas o ambas negativas). Si el objeto se está desacelerando, deben estar en direcciones opuestas. Imagínese que los gráficos de la Figura\(\PageIndex{1}\) describen el movimiento de una persona que corre con viento fuerte. En la gráfica de la izquierda, la persona está corriendo con el viento y acelerando (\(v(t)\)y\(a(t)\) positiva), y en la segunda gráfica la persona corre contra el viento y desacelerando (\(v(t)\)positiva y\(a(t)\) negativa).

Uso del cálculo para obtener la aceleración desde la posición

Supongamos que conocemos la función para la posición en función del tiempo, y que viene dada por nuestro resultado anterior (para el caso cuando la aceleración\(a_{x}\) es constante):

\[x(t)=x_0+v_{0x}t+\frac{1}{2}a_{x}t^{2}\]

Con nuestras definiciones basadas en cálculos anteriores, deberíamos poder recuperar eso:\[\begin{aligned} v(t) = v_{0x}t+at\\ a_x(t) = a_x\end{aligned}\] Empecemos determinando\(v(t)\):\[\begin{aligned} v(t) = \frac{dx}{dt}=\lim_{\Delta t\to 0} \frac{\Delta x}{\Delta t}\end{aligned}\] Conociendo nuestra función\(x(t)\), podemos reescribir esto como:\[\begin{aligned} \frac{dx}{dt}=\lim_{\Delta t\to 0} \frac{x(t+\Delta t)-x(t)}{\Delta t} \end{aligned}\] cual es la definición formal de la derivada\(\frac{dx}{dt}\) y nos da una receta para evaluarlo. Procederemos como se ilustra en la Figura\(\PageIndex{1}\):

1. Se usa\(x(t)\)\(\Delta x\) para determinar un intervalo pequeño\(\Delta t\)
2. Dividir\(\Delta x\) por\(\Delta t\)
3. Toma el límite,\(\lim_{\Delta t\to 0}\)

Para obtener\(\Delta x\), introducimos una hora de inicio\(t_1\), y una hora de finalización\(t_2\) para nuestro intervalo de tiempo, tal que\(t_2-t_1=\Delta t\), centrado alrededor de un tiempo\(t\). El cambio de posición viene dado entonces por:\[\begin{aligned} \Delta x &= x(t_2) - x(t_1)\\ &=\left(x_0+v_{0x}t_2+\frac{1}{2}a_xt_2^2\right )- \left(x_0+v_{0x}t_1+\frac{1}{2}a_xt_1^2\right )\\ &=v_{0x}(t_2-t_1)+\frac{1}{2}a_x(t_2^2-t_1^2)\\ &=v_{0x}\Delta t+\frac{1}{2}a_x(t_2-t_1)(t_2+t_1)\\ &=v_{0x}\Delta t+\frac{1}{2}a_x\Delta t (t_2+t_1)\\\end{aligned}\] que dividimos\(\Delta t\) para obtener\(v(t)\): Ahora\[\begin{aligned} v(t) &= \frac{\Delta x}{\Delta t}\\ &=\frac{v_{0x}\Delta t+\frac{1}{2}a_x\Delta t (t_2+t_1)}{\Delta t}\\ &=v_{0x}+\frac{1}{2}a_x(t_2+t_1)\end{aligned}\] tomamos el límite donde\(\Delta t\to 0\), es decir, cuando\(t_2-t_1\) es muy pequeño. A medida que hacemos pequeño el intervalo,\(t_2\) y\(t_1\) ambos nos acercaremos al mismo valor de tiempo\(t\), digamos, correspondiente al tiempo en el centro del intervalo. En particular, el promedio de\(t_1\) y\(t_2\), dado por\(\frac{1}{2}(t_1+t_2)\), se acercará al tiempo en el centro del intervalo,\(t\). Así recuperamos la ecuación para la velocidad instantánea: Por\[\begin{aligned} v(t) &= v_{0x}+a_xt\end{aligned}\] supuesto, una vez que te familiarices más con el cálculo, podrás usar directamente las fórmulas para derivadas para recuperar la respuesta:\[\begin{aligned} v(t) &= \frac{d}{dt}\left( x_0+v_{0x}t+\frac{1}{2}a_xt^2 \right) \\ &= v_{0x}+at \end{aligned}\] De igual manera, ahora podemos confirmar que la aceleración es una constante, independiente del tiempo: \[\begin{aligned} a_x(t) &= \frac{dv}{dt} = \frac{d}{dt}\left(v_{0x}+a_xt \right)\\ &=a_x\end{aligned}\]Puede verificar fácilmente que obtiene este resultado calculando primero\(v(t)\) en dos momentos diferentes,\(t_1\) y\(t_2\), tomando la diferencia,\(\Delta v = v(t_2)-v(t_1)\), y luego tomando el límite de\(\lim_{\Delta t\to 0}\frac{\Delta v}{\Delta t}\) para obtener \(a_x(t)\).

Ejercicio\(\PageIndex{1}\)

Chloë ha estado trabajando en un estudio detallado de cómo funcionan las vicuñas, y encontró que su posición en función del tiempo cuando empiezan a correr está bien modelada por la función\(x(t)=(40\text{m/s}^{2})t^{2}+(20\text{m/s}^{3})t^{3}\). What is the acceleration of the vicuñas?

1. \(a_x(t)=40\text{m/s}^{2}\)
2. \(a_x(t)=80\text{m/s}^{2}\)
3. \(a_x(t)=40\text{m/s}^{2}+(20\text{m/s}^{3})t\)
4. \(a_x(t)=80\text{m/s}^{2}+(120\text{m/s}^{3})t\)

“¿Nunca has oído hablar de las vicuñas? ¡Internet!

Contestar

Uso del cálculo para obtener la posición a partir de la aceleración

Ahora que vimos que podemos usar derivadas para determinar la aceleración desde la posición, veremos cómo hacer la marcha atrás y usar la aceleración para determinar la posición. Supongamos que tenemos una aceleración constante,\(a_{x}(t)=a_{x}\), y que sabemos que en el momento\(t=0\text{s}\), el objeto tenía una velocidad de\(v_{0x}\) y estaba localizado en una posición\(x_{0}\).

Como solo conocemos la aceleración en función del tiempo, primero necesitamos encontrar la velocidad en función del tiempo. Comenzamos con:

\[a_{x}(t)=a_{x}=\frac{d}{dt} v(t)\]

que nos dice que conocemos la pendiente (derivada) de la función\(v(t)\), pero no la función real. En este caso, debemos hacer lo contrario de tomar la derivada, que en cálculo se llama tomar la “anti-derivada” con respecto a\(t\) y tiene el símbolo\(\int dt\). En otras palabras, si:

\[\frac{d}{dt} v(t) =a_{x}(t)\]

entonces:

\[v(t) =\int a_{x}(t) dt +C\]

donde como veremos más adelante,\(C\) se requiere la constante para\(v(t)\) que la función pase por el punto\(v(t=0)=v_{0x}\). Todo lo que necesitamos ahora es determinar cómo calcular el antiderivado,\(\int a_{x}(t) dt\). Ya que en este caso,\(a_{x}(t)\) es una constante,\(a_{x}\), podemos determinar el anti-derivado con bastante facilidad.

Para un pequeño intervalo en el tiempo\(\Delta t\),, la velocidad cambiará en una pequeña cantidad\(\Delta v\),, tal que:\[\begin{aligned} a_x &= \frac{\Delta v}{\Delta t}\\ \Delta v &= a_x \Delta t\end{aligned}\] Si etiquetamos el tiempo de inicio del intervalo como\(t_1\) y el final del intervalo como\(t_2\), tenemos:\[\begin{aligned} \Delta t &= t_2 - t_1 \\ \Delta v &= v(t_2) - v(t_1) = a_x \Delta t\\ \therefore v(t_2) &= v(t_1)+a_x\Delta t\end{aligned}\] Si establecemos \(t_1=0\text{s}\)para corresponder al punto donde\(v(t)=v_{0x}\), entonces podemos escribir la velocidad a\(t_2\) como:\[\begin{aligned} v(t_2) = v(t=\Delta t) = v_{0x}+a_x\Delta t\end{aligned}\] y vemos que la velocidad cambió en una cantidad a\(a \Delta t\) lo largo de un periodo de tiempo\(\Delta t\). Ya que\(a_x\) es lo mismo en todo momento, esto siempre es cierto, y después de un periodo de tiempo\(t = N\Delta t\), la velocidad habrá cambiado por\(N a_x \Delta t\), y recuperamos la ecuación original para la velocidad en función del tiempo cuando la aceleración es constante:\[\begin{aligned} v(t=N \Delta t) &= v_{0x}+Na_x\Delta t\\ \therefore v(t) &= v_{0x}+a_xt\\\end{aligned}\] Nosotros puede identificar el anti-derivado para el caso donde\(a(t)\) es constante:\[\begin{aligned} \frac{d}{dt} v(t) &=a_x\\ \int a_x dt &=a_xt +C\end{aligned}\] donde la constante,\(C\), viene dada por\(v_{0x}\).

\[v(t)=C+a_{x}t=v_{0x}+a_{x}t\]

y recuperamos la fórmula de velocidad cuando la aceleración es constante. Ahora que conocemos la velocidad en función del tiempo, podemos tomar una anti-derivada más con respecto al tiempo para obtener la posición:

\(\begin{aligned}&v(t)=\frac{dx}{dt} \\ &\therefore x(t)=\int v(t)dt\end{aligned}\)

En el caso de que la aceleración sea constante, esto da:

\(\begin{aligned} x(t)&=\int v(t)dt \\ &=\int (v_{0x}+a_{x}t)dt \\ &=v_{0x}t+\frac{1}{2}a_{x}t^{2}+C' \end{aligned}\)

donde\(C'\) es una constante diferente a la que teníamos al determinar la velocidad. La constante viene dada por nuestras condiciones iniciales. Si el objeto estaba localizado en la posición\(x = x_{0}\) en el tiempo\(t = 0\), entonces\(C'= x_{0}\) y recuperamos la ecuación para la posición como una función del tiempo para la aceleración constante:

\[x(t)=x_{0}+v_{0x}t+\frac{1}{2}a_{x}t^{2}\]

Para obtener ahora la posición en función del tiempo, procedemos de la misma manera, a saber:

1. Definir un pequeño intervalo en el tiempo\(\Delta t\)
2. Calcular el cambio de posición correspondiente\(\Delta x\)
3. Agregue\(\Delta x\) a nuestra posición original, y repita.

Nuevamente, tenemos la derivada temporal de la posición igual a una función del tiempo:\[\begin{aligned} \frac{d}{dt}x(t)=v(t)=v_{0x}+a_xt\end{aligned}\] y necesitamos encontrar la anti-derivada:\[\begin{aligned} x(t) = \int \left( v_{0x}+av_xt \right) dt \end{aligned}\] dado que, en el momento\(t=0\), la posición era\(x=x_0\). Después de un pequeño intervalo en el tiempo\(\Delta t\),, la posición habrá cambiado en una cantidad\(\Delta x\): de\[\begin{aligned} \Delta x &= v(t) \Delta t\\\end{aligned}\] modo que la posición en el momento\(t=\Delta t\) estará dada por:\[\begin{aligned} x(t=\Delta t) &= x_0+ \Delta x\\ & = x_0+v(t) \Delta t\end{aligned}\] El problema aquí es evaluar\(v(t)\) ya que la velocidad cambia durante todo el intervalo. Una opción posible es evaluar la velocidad a\(t = \frac{1}{2}\Delta t\) la mitad del intervalo, como hicimos antes. También podríamos optar por usar la velocidad al principio o al final del intervalo de tiempo, ya que las tres opciones convergerán al mismo valor cuando\(\Delta t \to 0\). Por ahora, dejaremos abierta la elección y simplemente llamaremos a la velocidad que usamos\(v_1\) para indicar que es la velocidad en el primer intervalo. Escribimos así la posición,\(x(t=\Delta t)\), después de un intervalo de tiempo\(\Delta t\) como:\[\begin{aligned} x(t=\Delta t) = x_0+v_1\Delta t\end{aligned}\] La posición\(x(t=2\Delta t)\),, después de otro intervalo en el tiempo entonces\(\Delta t\) estará dada por:\[\begin{aligned} x(t=2\Delta t) &= x(t=\Delta t)+v_2\Delta t\\ &=x_0+v_1\Delta t+v_2\Delta t\end{aligned}\] donde\(v_2\) está la velocidad sobre el segundo intervalo en el tiempo (diferente a\(v_1\), ya que la velocidad cambia con el tiempo). Para el intervalo N, etiquetamos la posición\(x_N=x(t=N\Delta t)\):\[\begin{aligned} x_N=x(t=N\Delta t)&=x_0+v_1\Delta t+v_2\Delta t+\dots+v_N\Delta t\\ &=x_0+\sum_{i=1}^Nv_i\Delta t \end{aligned}\]

donde hicimos uso de la notación de suma (\(\sum\)) para evitar escribir cada término. La ecuación anterior sólo es correcta en el límite de\(\Delta t\to 0\), en cuyo caso debe ser la anti-derivada de\(v(t)\):\[\begin{aligned} x(t) &= \int v(t) dt\\ &= x_0+\lim_{\Delta t\to 0}\sum_{i=1}^Nv_i\Delta t \end{aligned}\] para que podamos identificar:

\[ \int v(t) dt=\lim_{\Delta t\to 0}\sum_{i=1}^Nv_i\Delta t + C \]

donde se entiende que\(v_i\) es la velocidad “promedio” en el intervalo i-ésimo, y la constante\(C=x_0\) asegura que\(x(t=0)=x_0\). Esta es ahora una definición general para el anti-derivado, ya que no hemos hecho ninguna suposición específica sobre la función\(v(t)\). La ecuación 3.3.10 nos dice que la anti-derivada de una función (en este caso,\(v(t)\)) se puede obtener de una suma.

La suma muestra la función\(v(t)\) y varios intervalos\(\Delta t\). Durante cada intervalo,\(i\), etiquetamos la velocidad promedio,\(v_i\). A medida que los intervalos se contraen\(\Delta t\to 0\),, la velocidad promedio\(v_i\) se acerca a la velocidad instantánea\(v(t)\),, en el centro para el intervalo. Dado que la función\(v(t)\) es lineal (para aceleración constante), la velocidad a la mitad de un intervalo es exactamente igual a la velocidad promedio en el intervalo. Tomando\(v_i\) como la velocidad en medio del intervalo, vemos entonces que cada término en la suma,\(v_i\Delta t\), es igual al área entre la curva\(v(t)\) y el eje t. Esto se ilustra para el segundo término en la suma,\(v_2\Delta t\).

La anti-derivada de una función se relaciona así con el área entre la función y el eje horizontal. Si especificamos límites en el eje horizontal entre los cuales calculamos el área, entonces el anti-derivado se llama integral. Por ejemplo, si queremos calcular la suma de\(v_i \Delta t\) para valores entre\(t_a\) y\(t_b\), escribiríamos la integral como:

\[ \int_{t_a}^{t_b}v(t) dt = \lim_{\Delta t\to 0}\sum_{i=1}^Nv_i\Delta t \]

donde la suma es tal que para\(i=1\),\(v_i\) está cerca de\(v(t=t_a)\) y para\(i=N\),\(v_N\) está cerca de\(v(t=t_b)\). Se muestra una ilustración de tomar la integral de donde\(v(t)\) se muestra la suma para dos valores diferentes de\(\Delta t\). Es claro que as\(\Delta t \to 0\), la suma se vuelve igual al área entre la curva y el eje horizontal.

Dado que\(v(t)\) es una función lineal cuando la aceleración es constante, podemos calcular fácilmente el área entre la curva y el eje horizontal. En el caso de una función lineal,\(v(t)=v_{0x}+at\), el área es un trapecio, y tenemos:

\[\begin{aligned} \int_{t_a}^{t_b}v(t) dt &= \text{base}\times\text{average height}\\ &=(t_b-t_a)\times\frac{1}{2}\left(v(t_a)+v(t_b)\right)\\ &=(t_b-t_a)\frac{1}{2}(v_{0x}+a_xt_a+v_{0x}+a_xt_b)\\ &=\left( \frac{1}{2}(v_{0x}t_b+a_xt_at_b+v_{0x}t_b+a_xt_b^2) \right)- \left( \frac{1}{2}(v_{0x}t_a+a_xt_a^2+v_{0x}t_a+a_xt_bt_a) \right)\\ &=\left( v_{0x}t_b+\frac{1}{2}a_xt_b^2 \right)-\left( v_{0x}t_a+\frac{1}{2}a_xt_a^2 \right)\end{aligned}\]

Si definimos una nueva función\(V(t)=v_{0x}t+\frac{1}{2}a_xt^{2}\),, entonces tenemos:

\[ \int_{t_{a}}^{t_{b}}v(t) dt = V(t_{b}) -V(t_{a})\]

En otras palabras, dada una función,\(v(t)\), la integral de esa función entre dos valores\(t_a\) y se\(t_b\) puede encontrar evaluando una función diferente,\(V(t)\), en los puntos finales\(t_a\) y\(t_b\). Como verás en tu curso de cálculo, la función\(V(t)\) es precisamente lo que llamamos el anti-derivado:

\[ \int v(t) dt= V(t) + C\]

que tiene derivado:\[\begin{aligned} \frac{dV}{dt}=v(t)\end{aligned}\] Tenga en cuenta que al tomar la integral, la constante\(C\) siempre cancela.

Ejercicio\(\PageIndex{2}\)

Elija la gráfica de\(x(t)\) para el caso cuando la aceleración viene dada por\(a(t) = Aω^{2}cos(ωt)\), donde\(ω\) y\(A\) son constantes positivas. La velocidad y la posición son cero a\(t = 0\).

Figura\(\PageIndex{2}\)

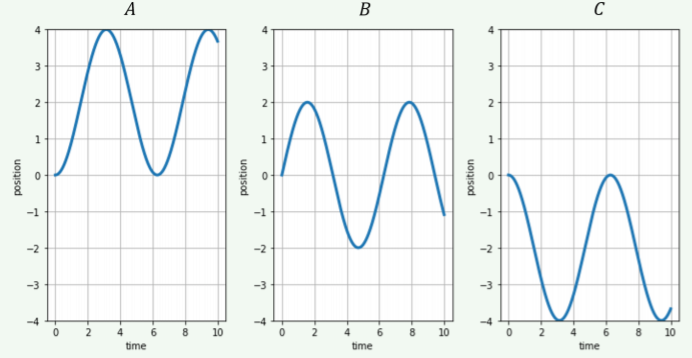
1. Figura A
2. Figura B
3. Figura C

Contestar

Ejercicio\(\PageIndex{3}\)

Se observa que la aceleración de un grillo saltando lateralmente aumenta linealmente con el tiempo, es decir,\(a_{x}(t)=a_{0}+jt\), where \(a_{0}\) and \(j\) are constants. What can you say about the velocity of the cricket as a function of time?

1. es constante
2. aumenta linealmente con el tiempo (\(v(t)\propto t\))
3. aumenta cuadráticamente con el tiempo (\(v(t)\propto t^{2}\))
4. aumenta con el cubo del tiempo (\(v(t)\propto t^{3}\))

Contestar