4.3: Movimiento acelerado cuando el vector de velocidad cambia de dirección

Una diferencia clave con el movimiento unidimensional es que, en dos dimensiones, es posible tener una aceleración incluso cuando la velocidad es constante. Recordemos, el vector de aceleración se define como la derivada de tiempo del vector de velocidad (Ecuación 4.1.4). Esto significa que si el vector de velocidad cambia con el tiempo, entonces el vector de aceleración es distinto de cero. Si la longitud del vector de velocidad (velocidad) es constante, aún es posible que la dirección del vector de velocidad cambie con el tiempo, y así, que el vector de aceleración sea distinto de cero. Esto es, por ejemplo, lo que sucede cuando un objeto da vueltas en círculo con una velocidad constante (la dirección del vector de velocidad cambia).

Figura\(\PageIndex{1}\): Ilustración de cómo puede cambiar la dirección del vector de velocidad cuando la velocidad es constante.

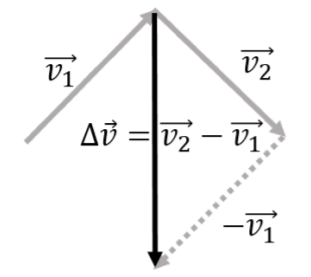
La figura\(\PageIndex{1}\) muestra una ilustración de un vector de velocidad\(\vec v(t)\), en dos momentos diferentes\(\vec v_2\),\(\vec v_1\) y, así como la diferencia vectorial,\(\Delta \vec v=\vec v_2 - \vec v_1\), entre los dos. En este caso, la longitud del vector de velocidad no cambió con time (\(||\vec v_1||=||\vec v_2||\)). El vector de aceleración viene dado por:

\[\begin{aligned} \vec a = \lim_{\Delta t\to 0}\frac{\Delta \vec v}{\Delta t}\end{aligned}\]

y tendrá una dirección paralela a\(\Delta \vec v\), y una magnitud que sea proporcional a\(\Delta v\). Así, incluso si el vector de velocidad no cambia la amplitud (la velocidad es constante), el vector de aceleración puede ser distinto de cero si el vector de velocidad cambia de dirección.

Escribamos el vector de velocidad\(\vec v\), en términos de su magnitud\(v\), y un vector unitario\(\hat v\), en la dirección de\(\vec v\):

\[\begin{aligned} \vec v &=v_x\hat x+v_y\hat y= v \hat v\\ v&=||\vec v||=\sqrt{v_x^2+v_y^2}\\ \hat v &= \frac{v_x}{v}\hat x+\frac{v_y}{v}\hat y\\\end{aligned}\]

En el caso más general, tanto la magnitud de la velocidad como su dirección pueden cambiar con el tiempo. Es decir, tanto la dirección como la magnitud del vector de velocidad son funciones del tiempo:

\[\begin{aligned} \vec v(t)&=v(t)\hat v(t)\end{aligned}\]

Cuando tomamos el tiempo derivado de\(\vec v(t)\) para obtener el vector de aceleración, necesitamos tomar la derivada de un producto de dos funciones del tiempo,\(v(t)\) y\(\hat v(t)\). Usando las reglas para tomar la derivada de un producto, el vector de aceleración viene dado por:

\[\begin{aligned} \vec a &= \frac{d}{dt}\vec v(t)= \frac{d}{dt}v(t)\hat v(t)\nonumber \end{aligned}\]

\[ \vec a = \frac{dv}{dt}\hat v(t)+v(t)\frac{d\hat v}{dt} \]

y tiene dos términos. El primer término,\(\frac{dv}{dt}\hat v(t)\), es cero si la velocidad es constante (\(\frac{dv}{dt}=0\)). El segundo término,\(v(t)\frac{d\hat v}{dt}\), es cero si la dirección del vector de velocidad es constante (\(\frac{d\hat v}{dt}=0\)). Sin embargo, en general, el vector de aceleración tiene dos términos correspondientes al cambio en la velocidad, y al cambio en la dirección de la velocidad, respectivamente.

La forma funcional específica del vector de aceleración dependerá de la ruta que esté tomando el objeto. Si consideramos el caso donde la velocidad es constante, entonces tenemos:

\[\begin{aligned} v(t) &= v \\ \frac{dv}{dt}&=0\\ v_x^2(t)+v_y^2(t) &=v^2 \\ \therefore v_y(t)&=\sqrt{v^2-v_x(t)^2}\end{aligned}\]

En otras palabras, si la magnitud de la velocidad es constante, entonces los\(y\) componentes\(x\) y ya no son independientes (si el\(x\) componente se hace más grande, entonces el\(y\) componente debe hacerse más pequeño para que la magnitud total permanezca sin cambios). Si la velocidad es constante, entonces el vector de aceleración viene dado por:

\[\begin{aligned} \vec a&=\frac{dv}{dt}\hat v(t)+v\frac{d\hat v}{dt}\nonumber\\ &=0 + v\frac{d}{dt}\hat v(t)\nonumber\\ &=v\frac{d}{dt}\left(\frac{v_x(t)}{v}\hat x+\frac{v_y(t)}{v}\hat y )\right)\nonumber\\ &=\frac{dv_x}{dt}\hat x + \frac{d}{dt}\sqrt{v^2-v_x(t)^2}\hat y\nonumber\\ &=\frac{dv_x}{dt}\hat x + \frac{1}{2\sqrt{v^2-v_x(t)^2}}(-2v_x(t))\frac{dv_x}{dt}\hat y\nonumber\\ &=\frac{dv_x}{dt}\hat x - \frac{v_x(t)}{\sqrt{v^2-v_x(t)^2}}\frac{dv_x}{dt}\hat y\nonumber\\ &=\frac{dv_x}{dt}\hat x - \frac{v_x(t)}{v_y(t)}\frac{dv_x}{dt}\hat y\nonumber \end{aligned}\]

\[\vec a=\frac{dv_{x}}{dt}\left( \hat x - \frac{v_{x}(t)}{v_{y}(t)}\hat y \right)\]

donde la mayor parte del álgebra que hicimos fue para separar los\(y\) componentes\(x\) y del vector de aceleración, y usamos la Regla de Cadena para tomar la derivada de la raíz cuadrada. El vector de aceleración resultante se ilustra en la Figura\(\PageIndex{2}\) junto con el vector de velocidad ¹.

Figura\(\PageIndex{2}\): Ilustración de que el vector de aceleración es perpendicular al vector de velocidad si la velocidad es constante.

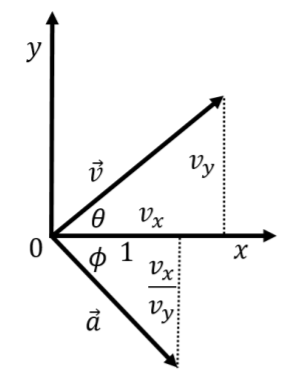
El vector de velocidad tiene componentes\(v_x\) y\(v_y\), lo que nos permite calcular el ángulo,\(\theta\) que hace con el\(x\) eje:

\[\begin{aligned} \tan(\theta)=\frac{v_y}{v_x}\end{aligned}\]

De igual manera, el vector que es paralelo a la aceleración tiene componentes de\(1\) y\(-\frac{v_x}{v_y}\), permitiéndonos determinar el ángulo\(\phi\),, que hace con el\(x\) eje:

\[\begin{aligned} \tan(\phi)=\frac{v_x}{v_y}\end{aligned}\]

Tenga en cuenta que\(\tan(\theta)\) es lo inverso de\(\tan(\phi)\), o en otras palabras,\(\tan(\theta)=\cot(\phi)\), lo que significa que\(\theta\) y\(\phi\) son complementarios y por lo tanto deben sumar a\(\frac{\pi}{2}\) (90). Esto significa que el vector de aceleración es perpendicular al vector de velocidad si la velocidad es constante y la dirección de la velocidad cambia.

En otras palabras, cuando escribimos el vector de aceleración, podemos identificar dos componentes,\(\vec a_{\parallel}(t)\) y\(\vec a_{\perp}(t)\):

\[\begin{aligned} \vec a&=\frac{dv}{dt}\hat v(t)+v(t)\frac{d\hat v}{dt}\\ &=\vec a_{\parallel}(t) + \vec a_{\perp}(t)\\ \therefore \vec a_{\parallel}(t)&=\frac{dv}{dt}\hat v(t)\\ \therefore \vec a_{\perp}(t)&=v\frac{d\hat v}{dt}=\frac{dv_x}{dt} \left(\hat x - \frac{v_x(t)}{v_y(t)}\hat y\right)\end{aligned}\]

donde\(\vec a_{\parallel}(t)\) es el componente de la aceleración que es paralelo al vector de velocidad, y es responsable de cambiar su magnitud, y\(\vec a_{\perp}(t)\), es el componente que es perpendicular al vector de velocidad y es responsable de cambiar la dirección del movimiento.

Ejercicio\(\PageIndex{1}\)

Un satélite se mueve en órbita circular alrededor de la Tierra con una velocidad constante. ¿Qué puedes decir de su vector de aceleración?

1. Tiene una magnitud de cero.
2. Es perpendicular al vector de velocidad.
3. Es paralelo al vector de velocidad.
4. Se encuentra en una dirección distinta a la paralela o perpendicular al vector de velocidad.

Contestar

Notas al pie

1. Más bien, es un vector paralelo al vector de aceleración que se ilustra, ya que\(\frac{dv_{x}}{dt}\) se omitió el factor de (como se recuerda, multiplicar por un escalar solo cambia la longitud, no la dirección)