4.7: Problemas y soluciones de muestra

Ejercicio\(\PageIndex{1}\)

Ethan está saltando obstáculos. Se pone un arranque a correr, moviéndose con una velocidad de\(3\text{m/s}\). The hurdle is \(0.5\text{m}\) high and the maximum speed that he can have when he leaves the ground is \(5\text{m/s}\). (You can assume Ethan is a point particle, and ignore air resistance).

1. ¿Cuál es la distancia más cercana del obstáculo al que Ethan puede saltar y aún así despejar el obstáculo?
2. ¿Qué altura máxima alcanza?

Contestar

Nuestro enfoque será considerar los\(y\) componentes\(x\) y de la moción por separado. Comenzamos dibujando un diagrama y eligiendo nuestro sistema de coordenadas. Elegiremos\(y\) ser verticales y positivos hacia arriba y\(x\) estar en la dirección que está corriendo Ethan. Elegimos el origen para ser el lugar donde Ethan deja el suelo para el salto, como se ilustra en la Figura\(\PageIndex{1}\).

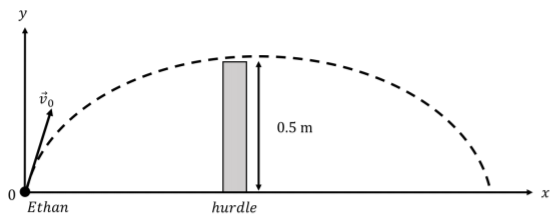
Figura\(\PageIndex{1}\): Ethan quiere despejar un\(0.5\text{ m}\) obstáculo y tiene una velocidad inicial\(\vec v_{0}\) con\(x\) y\(y\) componentes.

a. La velocidad de Ethan al inicio del salto es\(v_0=5\text{m/s}\) y la componente horizontal (\(x\)) de su velocidad es\(v_x=3\text{m/s}\). El\(y\) componente de su velocidad inicial,\(v_{0y}\), viene dado por:\[\begin{aligned} v_x^2+v_{0y}^2&=v_0^2\\ v_{0y}&=\sqrt{v_0^2-v_x^2}\\ v_{0y}&=\sqrt{(5\text{m/s})^2-(3\text{m/s})^2}=4\text{m/s}\end{aligned}\] Elegimos el origen al inicio del salto, de manera que las de Ethan\(x\) y las\(y\) coordenadas en el momento\(t=0\) son\(x_0=0\) y\(y_0=0\), respectivamente. Una vez que Ethan esté en el aire, no habrá aceleración en la\(x\) dirección, y la única aceleración es en la\(y\) dirección y será esa por gravedad. La posición de Ethan en cualquier momento\(t\) puede ser descrita por las siguientes ecuaciones:\[\begin{aligned} x(t)&=v_{x}t\\ y(t)&=v_{0y}t-\frac{1}{2}gt^2\end{aligned}\] donde\(g\) está la aceleración debida a la gravedad,\(g=9.8\text{m/s^2}\).

Queremos determinar el valor de\(x(t)\) cuando el desplazamiento vertical,\(y(t)\), es igual a la altura del obstáculo,\(h\). Así encontramos el valor de\(t\) cuándo\(y=0.5\text{m}\) y luego encontramos el valor de\(x\) en ese momento.

Podemos reorganizar la ecuación para\(y(t)\) y resolver la cuadrática resultante para\(t\) (obtenemos dos soluciones):\[\begin{aligned} 0&=-\frac{1}{2}gt^2+v_{0y}t-h\\ 0&=\frac{1}{2}(-9.8\text{m/s}^{2})t^2+(4\text{m/s})t-0.5\text{m}\\ t&=0.15\text{s},\quad 0.66\text{s}\end{aligned}\] El salto será una parábola, y Ethan cruzará una altura de\(0.5\text{m}\) dos veces, una vez en el camino hacia arriba y otra en el camino hacia abajo. Queremos saber cuándo llega Ethan\(0.5\text{m}\) por primera vez (en el camino hacia arriba), así que elegimos\(t=0.15\text{s}\). El desplazamiento horizontal en este momento es:\[\begin{aligned} x&=v_xt\\ &=(3\text{m/s})(0.15\text{s})\\ &=0.45\text{m}\end{aligned}\] Por lo tanto, puede acercarse tanto como\(0.45\text{m}\) desde el obstáculo antes de que tenga que saltar, si su velocidad horizontal inicial es\(3\text{m/s}\).

b. El movimiento de Ethan sigue una forma parabólica. A la altura máxima, la velocidad vertical de Ethan es igual a cero. Podemos modelar solo la parte vertical del movimiento para resolver por el valor de\(y\) cuándo\(v_y=0\). Conocemos las siguientes cantidades:\[\begin{aligned} v_{0y}&=4\text{m/s}\\ v_y&=0\test{m/s}\\ g&=9.8\text{m/s}^{2}\end{aligned}\] La forma más fácil de determinar\(y\) es usar la fórmula,\[\begin{aligned} v_y^2&=v_{0y}^2-2g(y-y_0)\\ \therefore y&=\frac{v_y^2-v_{0y}^2}{(-2g)}\end{aligned}\] Sustituyendo nuestros valores por\(v_y\)\(v_{0y}\),, y\(g\), obtenemos:\[\begin{aligned} y_{max}&=\frac{(-4\text{m/s})^2}{(2)(-9.8\text{m/s}^{2})}\\ y_{max}&=0.82\text{m}\end{aligned}\] Ethan alcanza una altura máxima de \(0.82\text{m}\).

Ejercicio\(\PageIndex{2}\)

Un vaquero balancea un lazo por encima de su cabeza. El Lazo se mueve a una velocidad constante en un círculo de radio\(1.5\text{m}\) in the horizontal plane. A hawk flies toward the lasso at \(50\text{km/h}\). The hawk sees the end of the lasso moving at \(60\text{km/h}\) when the lasso is directly in front of it (see Figure \(\PageIndex{2}\)). In the reference frame of the cowboy ...

1. ¿Cuánto tiempo tarda el lasso en completar una revolución? (Pista: Desde el punto de vista del halcón, el lasso se mueve hacia él además de moverse en círculo. ¡Tendrás que usar tus conocimientos de movimiento relativo para resolver este problema!)
2. ¿Cuál es la aceleración centrípeta del final del Lazo?
3. ¿Cuál es la aceleración angular del lasso?

Figura\(\PageIndex{2}\): El problema visto desde arriba. Este diagrama representa el momento en que el final del Lazo pasa frente al halcón.

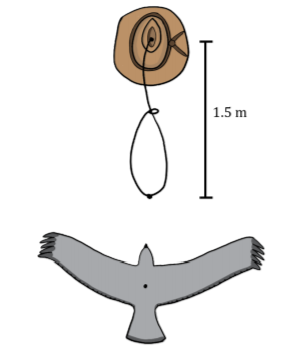
Contestar

a. necesitamos determinar la velocidad del final del lasso en el marco de referencia del vaquero, conociendo su velocidad en el marco de referencia del halcón y conociendo la velocidad del halcón. Una vez que conocemos la velocidad del Lazo en el marco de referencia del vaquero podemos determinar fácilmente cuánto tiempo lleva completar una revolución (su periodo).

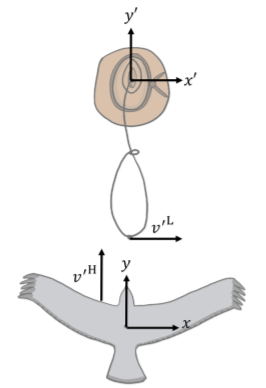
Figura\(\PageIndex{3}\): Los dos sistemas de coordenadas están alineados de manera que positivo\(y^{'}\) y positivo\(y\) estén en la misma dirección. Se muestran los vectores de velocidad del halcón y el Lazo en el marco de referencia del vaquero.

Comenzamos introduciendo sistemas de coordenadas para el halcón (\(xy\)) y el vaquero (\(x'y'\)), y elegimos que los ejes\(x\)\(x'\) (\(y\)\(y'\)) y () sean paralelos. Elegimos los ejes de tal manera que\(x\) está a la derecha (cuando se ve desde arriba, como en la Figura\(\PageIndex{3}\)) y\(y\) está en la dirección de movimiento del halcón como se ve en el marco de referencia del vaquero. El vector de velocidad del halcón en el marco de referencia del vaquero es:\[\begin{aligned} \vec v'_H = v'_H \hat y = (50{km/h})\hat y\end{aligned}\] En el marco de referencia del halcón, el Lazo tendrá un\(y\) componente de velocidad en\(y\) dirección negativa con la misma magnitud que la velocidad del halcón, y un componente desconocido ,\(v_{Lx}\), en la\(x\) dirección. La velocidad del Lazo en el marco de referencia del halcón es:\[\begin{aligned} \vec v_L=v_{Lx}\hat x - v'_H \hat y\end{aligned}\] Sin embargo, conocemos la velocidad del Lazo en el marco de referencia del halcón (\(v_L=60\text{km/h}\)), por lo que podemos encontrar fácilmente\(v_{Lx}\):\[\begin{aligned} v_{Lx}=\sqrt{v_L^2-v'^2_H}=\sqrt{(60\text{km/h})^2-(50\text{km/h})^2}=33.17\text{km/h}\end{aligned}\]

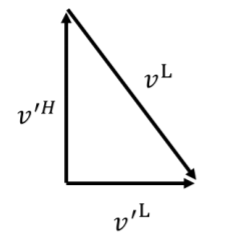
Figura\(\PageIndex{4}\): Adición de vectores para determinar la velocidad del Lazo en el marco de referencia del vaquero.

En el marco de referencia del vaquero, el Lazo tendrá un vector de velocidad (Figura 4.7.4),\(\vec v'_L\), dado por: Es\[\begin{aligned} \vec v'_L &= \vec v'_H + \vec v_L\\ &= v'_H \hat y + v_{Lx}\hat x - v'_H \hat y\\ &=v_{Lx}\hat x = (33.17\text{km/h})\hat x\end{aligned}\] decir, en el marco de referencia del vaquero, el Lazo tiene una velocidad que está en la\(x\) dirección. Esto corresponde a la velocidad,\(v_s\), del extremo del Lazo en movimiento circular uniforme alrededor de un círculo de radio\(R=1.5\text{m}\). Así podemos encontrar el tiempo requerido para que una revolución sea:\[\begin{aligned} v_s &= \frac{2\pi R}{T}\\ \therefore T &= \frac{2\pi R}{v_s} =\frac{2\pi (1.5\text{m})}{(33.17\text{km/h})} = \frac{2\pi (1.5\text{m})}{(9.2\text{m/s})}=1.02\text{s}\end{aligned}\] donde convertimos la velocidad\(\text{m/s}\) antes de determinar el tiempo.

b. el movimiento es movimiento circular uniforme, por lo que tiene una aceleración centrípeta dada por\[\begin{aligned} a_c(t)&=\frac{v_s^2(t)}{R}\end{aligned}\] Para encontrar la aceleración centrípeta del extremo del lasso, solo usamos nuestros valores para\(v_s\) y\(R\). \[\begin{aligned} a_c(t)&=\frac{(9.2\text{m/s})^2}{1.5\text{m}}=56\text{m/s}^{2}\end{aligned}\]

c. La aceleración angular del Lazo es cero. La aceleración angular se refiere a la velocidad de cambio de la velocidad angular (la velocidad a la que gira el Lazo), que es constante para un movimiento circular uniforme.