5.4: Aplicando las leyes de Newton

Ahora que hemos introducido todos los conceptos de la Teoría de la Física Clásica de Newton, presentamos algunas estrategias generales para construir modelos que utilicen la teoría. Recordemos que si podemos describir el movimiento de todos los objetos de interés para nosotros, hemos descrito todo lo que podemos. La Segunda Ley de Newton nos permite determinar la aceleración de un objeto a partir de la fuerza neta que actúa sobre el objeto. Una vez que hemos determinado las aceleraciones de todos los objetos de interés, hemos construido un modelo completo.

El paso más importante en la aplicación de la Teoría de Newton es identificar las fuerzas que se ejercen sobre un objeto. El paso más importante en la aplicación de la Teoría de Newton es identificar las fuerzas que se ejercen sobre un objeto. El paso más importante en la aplicación de la Teoría de Newton es identificar las fuerzas que se ejercen sobre un objeto. Ahora que lo has leído tres veces, te das cuenta de que este paso es importante, ¿verdad?

La estrategia para construir un modelo para el movimiento de un objeto usando la Teoría de Newton es sencilla:

1. Identificar un marco inercial de referencia en el que construir el modelo.
2. Identificar las fuerzas que actúan sobre el objeto (¿mencionamos que este paso es importante?).
3. Dibuja un diagrama de cuerpo libre.
4. Aplicar la Segunda Ley de Newton.

Identificar las fuerzas

El primer paso para aplicar la teoría de Newton es identificar todas las fuerzas que están actuando sobre un objeto. Esto se puede hacer preguntándose: “¿qué podría ser empujar o tirar del objeto?” , así como recorrer la lista de fuerzas que enumeramos en la Sección 5.2 para identificar si alguna de ellas es relevante aquí. Para una fácil referencia, aquí reproducimos los tipos de fuerzas e incluimos algunas preguntas que podrías hacerte para decidir si incluir o no la fuerza correspondiente:

• Peso (¿el objeto está cerca de la superficie de un planeta?).
• Fuerzas normales (¿el objeto está en contacto con alguna superficie? ¡Podría haber más de uno!).
• Fuerzas de fricción (¿hay fuerzas de fricción estáticas o cinéticas asociadas con las fuerzas normales?).
• Fuerzas de tensión (¿es algo así como una cuerda tirando del objeto?).
• Fuerzas de arrastre (¿el objeto se mueve a través de un fluido?).
• Fuerzas de resorte (¿hay un resorte que empuja o tira del objeto?).
• Fuerzas aplicadas (¿hay algo más que empuja o tira del objeto?).

Ejemplo\(\PageIndex{1}\)

Figura\(\PageIndex{1}\): Un bloque sobre una mesa horizontal.

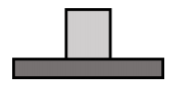
Un bloque de masa\(m\) está en reposo sobre una mesa horizontal, como se muestra en la Figura\(\PageIndex{1}\). ¿Qué fuerzas se ejercen sobre el bloque?

Solución:

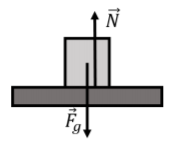
Las fuerzas sobre el bloque se ilustran en la Figura\(\PageIndex{2}\) y son:

1. \(\vec F_g\), su peso.
2. \(\vec N\), una fuerza normal ejercida por el avión. La fuerza normal es perpendicular a la interfaz entre la mesa y el bloque. Señala hacia arriba en “reacción” a la fuerza descendente que el bloque ejerce sobre la mesa. No se muestra la fuerza hacia abajo desde el bloque sobre la mesa, ya que esa fuerza no se ejerce sobre el bloque sino sobre la mesa.

Figura\(\PageIndex{2}\): Fuerzas sobre un bloque sobre una mesa horizontal.

Ejemplo\(\PageIndex{2}\)

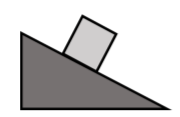
Un bloque de masa\(m\) is at rest on a inclined surface, as shown in Figure 5.4.3. What forces are exerted on the block?

Figura\(\PageIndex{3}\): Un bloque sobre una superficie inclinada.

Solución:

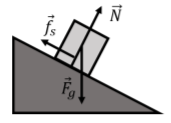
Las fuerzas sobre el bloque se ilustran en la Figura\(\PageIndex{4}\) y son:

1. \(\vec F_g\), su peso.
2. \(\vec N\), una fuerza normal ejercida por el plano inclinado.
3. \(\vec f_s\), una fuerza de fricción estática ejercida por el plano inclinado. Sin esta fuerza, el bloque se deslizaría hacia abajo. La fuerza está en la dirección opuesta a impedir el movimiento y es paralela a la interfaz (y perpendicular a la fuerza normal).

Figura\(\PageIndex{4}\): Fuerzas en bloque sobre una superficie inclinada.

Ejemplo\(\PageIndex{3}\)

Figura\(\PageIndex{5}\): Un bloque que descansa sobre un bloque en forma de cuña.

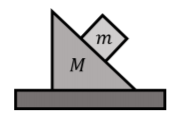
Un bloque de masa\(m\) is at rest on a wedge-shaped block of mass \(M\) itself at rest on a horizontal table, as shown in Figure \(\PageIndex{5}\). What forces are exerted on each of the two blocks?

Solución:

Como va a ser demasiado desordenado dibujar todas las fuerzas en un mismo diagrama, hemos dibujado cada bloque por separado en la Figura\(\PageIndex{5}\). Por lo general, cuando se apilan varios bloques entre sí, es más fácil comenzar con las fuerzas en el bloque superior. En este caso, el bloque superior está en las mismas condiciones que el bloque del Ejemplo 5.4.2. Las fuerzas ejercidas sobre el bloque superior son:

1. \(\vec F_g^m\), su peso.
2. \(\vec N^m\), una fuerza normal del bloque en forma de cuña.
3. \(\vec f_s^m\), una fuerza de fricción estática ejercida por el bloque en forma de cuña.

Las fuerzas ejercidas sobre el bloque en forma de cuña son:

1. \(\vec F_g^M\), su peso.
2. \(\vec N^M\), una fuerza normal ejercida por el pequeño bloque. Tenga en cuenta que esta fuerza es igual en magnitud y opuesta en dirección a\(\vec N^m\) (las dos fuerzas,\(\vec N^m\) y\(\vec N^M\), que están en diferentes objetos, son un par de fuerzas de acción/reacción).
3. \(\vec f_s^M\), una fuerza de fricción ejercida por el pequeño bloque (de nuevo, esto forma un par de fuerzas de acción/reacción con\(\vec f_s^m\)).
4. \(N_2^M\), una fuerza normal ejercida por la mesa.

Las fuerzas para ambos bloques se muestran en la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): Fuerzas sobre el bloque y el bloque en forma de cuña.

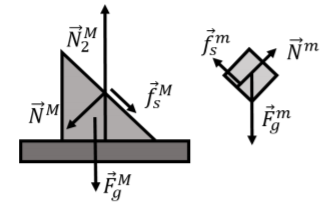
Diagramas de cuerpo libres

Para analizar más claramente las fuerzas sobre un objeto, es muy buena idea dibujar un “Diagrama de Cuerpo Libre” (FBD). Un diagrama de cuerpo libre es simplemente un diagrama donde dibujamos las fuerzas sobre un solo objeto y representamos el objeto como un punto. Debido a que el objeto es un punto, no nos preocupamos en qué parte del objeto se ejercen las fuerzas. En capítulos posteriores, veremos que para los cuerpos extendidos, sí importa dónde se apliquen las fuerzas. No obstante, las Leyes de Newton tal como se han presentado hasta ahora sólo son válidas para objetos que pueden representarse como un pequeño punto.

Figura\(\PageIndex{7}\): Diagrama de cuerpo libre para el bloque y el bloque en forma de cuña del Ejemplo 5.4.3.

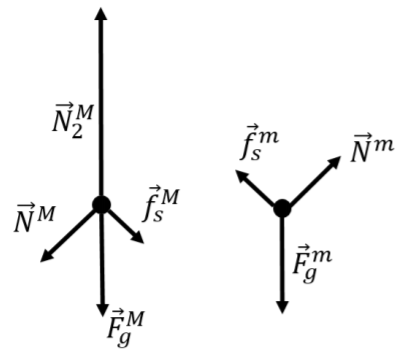
En el Ejemplo 5.4.3 anterior, dibujaríamos un diagrama de cuerpo libre para cada objeto (cada masa), como se muestra en la Figura\(\PageIndex{7}\).

Ejemplo\(\PageIndex{4}\)

Figura\(\PageIndex{8}\): Dos bloques conectados deslizándose por un plano inclinado.

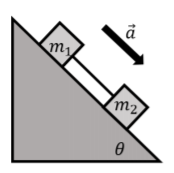
Dos bloques, de masas\(m_{1}\) y\(m_{2}\), se colocan en un plano inclinado que hace un ángulo\(θ\) con la horizontal. Los bloques están conectados por una cuerda sin masa, como se muestra en la Figura\(\PageIndex{8}\). Los dos bloques se deslizan y aceleran hacia abajo con una aceleración,\(\vec a\), como se muestra. El coeficiente de fricción cinética entre el plano y cualquiera de los bloques es\(µ_{k}\). Dibuja un diagrama de cuerpo libre para cada bloque.

Solución:

Primero, identificamos las fuerzas en cada masa (cada bloque), que luego usamos para hacer el diagrama de cuerpo libre que se muestra en la Figura\(\PageIndex{8}\). En masa\(m_1\), las fuerzas son:

1. \(\vec F_{g1}\), su peso.
2. \(\vec N_1\), una fuerza normal ejercida por el plano inclinado.
3. \(\vec f_{k1}\), una fuerza de fricción cinética ejercida por el plano inclinado. La fuerza está en la dirección opuesta al movimiento, y tiene una magnitud dada por\(f_{k1}=\mu_kN_1\).
4. \(\vec T\), una fuerza de tensión de la cuerda.

En masa\(m_2\), las fuerzas son:

1. \(\vec F_{g2}\), su peso.
2. \(\vec N_2\), una fuerza normal desde el plano inclinado.
3. \(\vec f_{k2}\), una fuerza de fricción cinética ejercida por el plano inclinado. La fuerza está en la dirección opuesta al movimiento, y tiene una magnitud dada por\(f_{k2}=\mu_kN_2\).
4. \(-\vec T\), una fuerza de tensión de la cuerda. Esta es la misma fuerza que on\(m_1\), pero en sentido contrario. Elegimos etiquetar la fuerza como\(-\vec T\), en lugar de usar una variable diferente, ya que es solo el negativo del vector lo que representa la fuerza de tensión en\(m_1\).

En la Figura\(\PageIndex{9}\), hemos mostrado las fuerzas en cada bloque utilizando un diagrama de cuerpo libre. También reprodujimos el vector para la aceleración (dibujamos el vector para la aceleración usando una flecha más gruesa para indicar que tiene una dimensión diferente). También reprodujimos el ángulo\(\theta\) en el diagrama de cuerpo libre, ya que esto es útil una vez que el diagrama de cuerpo libre se usa con la Segunda Ley de Newton.

Figura\(\PageIndex{8}\).

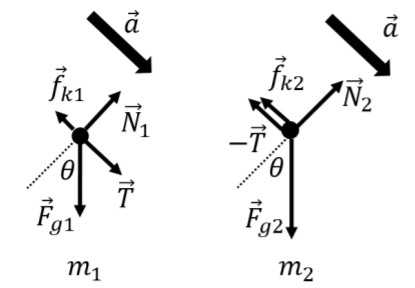
Usando la Segunda Ley de Newton

Aplicar la Segunda Ley de Newton es sencillo una vez que se han identificado todas las fuerzas ejercidas sobre un objeto. Por lo tanto, debe asegurarse de pasar la mayor parte del tiempo dibujando un diagrama de cuerpo libre bueno y completo antes de continuar.

La Segunda Ley de Newton es una ecuación vectorial que relaciona la suma vectorial de todas las fuerzas ejercidas sobre un objeto y el vector de aceleración del objeto. Esto corresponde a una ecuación escalar por componente del vector.

\[\begin{aligned} \sum \vec F &=m\vec a\\ \sum F_x &= ma_x \\ \sum F_y &= ma_y \\ \sum F_z &= ma_z\end{aligned}\]

Para utilizar la Segunda Ley de Newton, necesitamos introducir un sistema de coordenadas para que podamos trabajar con los componentes de los vectores (fuerzas y aceleración) en ese sistema de coordenadas. Por lo general, una buena opción de sistema de coordenadas es aquel en el que el eje\(x\) (o\(y\)) es paralelo al vector de aceleración. La figura\(\PageIndex{10}\) muestra el diagrama de cuerpo libre del\(m_1\) bloque del ejemplo anterior (Ejemplo 5.4.4) junto con una buena elección del sistema de coordenadas.

Figura\(\PageIndex{9}\), Ejemplo 5.4.4.

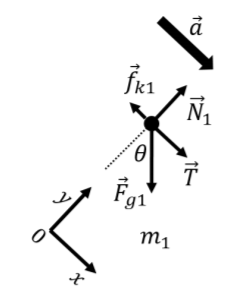
Para aplicar la Segunda Ley de Newton usando el diagrama de cuerpo libre y el sistema de coordenadas de la Figura\(\PageIndex{10}\), primero escribimos todo el vector y luego identificamos sus\(y\) componentes\(x\) y. Los vectores de fuerza son: Ahora\[\begin{aligned} \vec T &= T\hat x+0\hat y\\ \vec f_{k1}&=-f_{k1}\hat x+0\hat y\\ \vec F_{g1}&=m_1g(\sin\theta \hat x-\cos\theta \hat y)\\ \vec N_1&=0\hat x+N_1\hat y\end{aligned}\] podemos escribir el\(x\) componente de la Segunda Ley de Newton:\[\begin{aligned} \sum F_x = T-f_{k1}-F_{g1}\sin\theta &= m_1 a\\ \therefore T-f_{k1}-F_{g1}\sin\theta &= m_1 a\end{aligned}\] donde observamos que la fuerza normal no tiene componente en la\(x\) dirección. El\(y\) componente de la Segunda Ley de Newton para la masa\(m_1\) viene dado por:\[\begin{aligned} \sum F_y = N_1-F_{g1}&=0\\ \therefore N_1-F_{g1}&=0\end{aligned}\] donde observamos que las fuerzas de tensión y fricción no tienen\(y\) componente alguno. Las dos ecuaciones que obtuvimos anteriormente para\(x\) y especifican\(y\) completamente el movimiento del\(m_1\) bloque si se conocen todas las cantidades ³.

Algunas notas sobre la aplicación de la Segunda Ley de Newton:

• Al aplicar la Segunda Ley de Newton, analice cada masa en el problema por separado. No importa que el bloque\(m_1\) esté conectado por una cuerda a bloquear\(m_2\). Una vez que hayas determinado todas las fuerzas ejercidas sobre\(m_1\) ellas, puedes escribir la Segunda Ley de Newton para\(m_1\).
• La Segunda Ley de Newton es una ecuación vectorial; esto significa que es cierta para cada componente (escalar) de los vectores involucrados.
• Puede elegir el sistema de coordenadas, así que elija uno que facilite la escritura de los componentes vectoriales. Una buena opción es elegir\(x\) ser paralelo al vector de aceleración, para que no tengas que romper el vector de aceleración en componentes. La elección del sistema de coordenadas solo se realiza para permitirle escribir los componentes de la Segunda Ley de Newton con base en el diagrama de cuerpo libre.
• Tratar cada masa por separado (ya que la Segunda Ley de Newton solo es cierta para una masa individual). Esto significa que cada masa tendrá su propio diagrama de cuerpo libre y que puede elegir el sistema de coordenadas que sea más conveniente para un diagrama de cuerpo libre dado. En particular, esto significa que no es necesario elegir el mismo sistema de coordenadas para diferentes masas en un problema.

El siguiente ejemplo muestra cómo escribir la Segunda Ley de Newton para un sistema de dos bloques.

Ejemplo\(\PageIndex{5}\)

Figura\(\PageIndex{11}\): Dos bloques conectados por una cuerda sin masa y una polea sin masa. Ambos bloques se están acelerando.

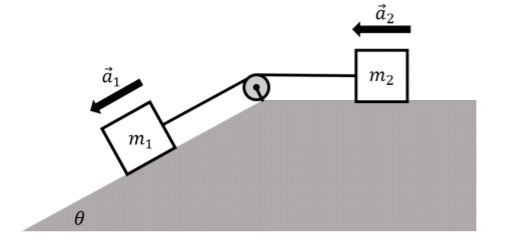
Un bloque de masa\(m_1\) is placed on an incline that makes an angle of \(\theta\) with the horizontal. The block of mass \(m_1\) is connected by a massless string through a massless pulley to a second block of mass \(m_2\), which rests on a horizontal surface. The blocks are accelerating in such a way that the block of mass \(m_1\) is accelerating down the incline, as shown in Figure \(\PageIndex{5}\). The coefficient of kinetic friction between either block and the surface it is resting on is \(\mu_k\). Write Newton’s Second Law for both blocks.

Solución:

Primero, identificamos las fuerzas en cada masa (cada bloque). En masa\(m_1\), las fuerzas son:

1. \(\vec F_{g1}\), su peso.
2. \(\vec N_1\), una fuerza normal ejercida por el plano inclinado.
3. \(\vec f_{k1}\), una fuerza de fricción cinética ejercida por el plano inclinado. La fuerza está en la dirección opuesta al movimiento, y tiene una magnitud dada por\(f_{k1}=\mu_kN_1\).
4. \(\vec T_1\), una fuerza de tensión de la cuerda.

En masa\(m_2\), las fuerzas son:

1. \(\vec F_{g2}\), su peso.
2. \(\vec N_2\), una fuerza normal desde la superficie horizontal.
3. \(\vec f_{k2}\), una fuerza de fricción cinética ejercida por la superficie horizontal. La fuerza está en la dirección opuesta al movimiento, y tiene una magnitud dada por\(f_{k2}=\mu_kN_2\).
4. \(\vec T_2\), una fuerza de tensión de la cuerda. Esta fuerza tiene la misma magnitud que la fuerza de tensión\(\vec T_1\) ejercida sobre la masa\(m_1\), debido a que la polea es sin masa.

Entonces podemos proceder a dibujar el diagrama de cuerpo libre para cada masa, y usarlo para escribir la Segunda Ley de Newton. Para la masa\(m_1\), el diagrama de cuerpo libre se muestra en la Figura\(\PageIndex{12}\). Hemos elegido un sistema de coordenadas que tiene el\(x\) eje paralelo a la aceleración del bloque, y el\(y\) eje hacia arriba y perpendicular al\(x\) eje, como se muestra.

Figura\(\PageIndex{12}\): Diagrama de cuerpo libre para\(m_{1}\).

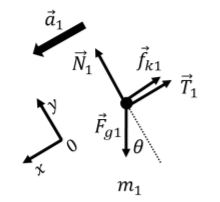
Para\(m_1\), podemos escribir la Segunda Ley de Newton, comenzando por los\(x\) componentes:\[\begin{aligned} \sum F_x = F_{g1}\sin\theta-f_{k1}-T_1&=m_1a_1\\ \therefore m_1 g\sin\theta -\mu_k N_1 - T_1 &= m_1 a_1\end{aligned}\] donde, en la segunda línea, se utilizó la magnitud del peso (\(F_{g1}=m_1g\)) y de la fuerza de fricción cinética (\(f_{k1}=\mu_kN_1\)). Para el\(y\) componente de la Segunda Ley de Newton, en el que la aceleración no tiene componente, tenemos:\[\begin{aligned} \sum F_y = N_1 - F_{g1}\cos\theta &= 0\\ \therefore N_1=m_1g\cos\theta\end{aligned}\] lo que nos demuestra que la magnitud de la fuerza normal puede expresarse fácilmente en términos del peso (\(F_{g1}=m_1g\)) y el ángulo de la inclinación.

Para\(m_2\), podemos proceder de la misma manera, eligiendo un sistema de coordenadas diferente, ya que el vector de aceleración para\(m_2\) puntos en una dirección diferente (no tenemos que elegir un sistema de coordenadas diferente, pero podemos si lo encontramos facilita las cosas). El diagrama de cuerpo libre para\(m_2\) se muestra en la Figura\(\PageIndex{13}\) junto con nuestra elección del sistema de coordenadas.

Figura\(\PageIndex{13}\): Diagrama de cuerpo libre para\(m_{2}\).

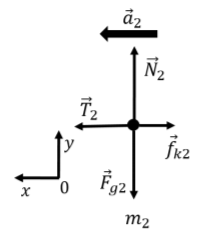
Comenzamos por escribir el\(x\) componente de la Segunda Ley de Newton para\(m_2\):\[\begin{aligned} \sum F_x = T_2 - f_{k2} &= m_2 a_2\\ \therefore T_2 - \mu_k N_2 = m_2 a_2\end{aligned}\] donde nuevamente, expresamos la fuerza cinética de fricción usando la fuerza normal y el coeficiente de fricción cinética. El\(y\) componente de la Segunda Ley de Newton da:\[\begin{aligned} \sum F_y = F_{g2}-N_2 &=0\\ \therefore N_2 = m_2g\end{aligned}\] donde nuevamente, expresamos el peso en términos de la masa y\(g\), y encontramos que la fuerza normal tiene la misma magnitud que el peso.

Ahora que hemos escrito la Segunda Ley de Newton para cada masa, podemos escribir las cuatro ecuaciones que obtuvimos para describir el sistema de dos masas. También hay que señalar que la magnitud de las fuerzas de tensión son las mismas para las dos masas (\(T_1=T_2=T\)), y que como las masas están conectadas por una cuerda, la magnitud de sus vectores de aceleración es la misma (\(a_1=a_2=a\)). Usando esto, podemos describir el sistema completo con las siguientes 4 ecuaciones: De\[\begin{aligned} m_1 g\sin\theta -\mu_k N_1 - T &= m_1 a\\ N_1=m_1g\cos\theta\\ T - \mu_k N_2 = m_2 a\\ N_2 = m_2g\end{aligned}\] las variables anteriores (\(m_1\),,,,,\(m_2\),\(\mu_k\),)\(T\)\(N_1\),\(N_2\),,,\(a\)), una solo necesitan especificar todos menos cuatro de ellos para describir completamente el movimiento del sistema. Por ejemplo, si se especifican las dos masas y el coeficiente de fricción cinética, se pueden determinar todas las demás variables.

Notas al pie

3. Como tenemos dos ecuaciones, técnicamente solo necesitamos especificar todas menos dos cantidades para poder modelar completamente el movimiento del bloque.