5.6: Marcos no inerciales de referencia y fuerzas inerciales

En las secciones anteriores, describimos cómo utilizar la Primera Ley de Newton para identificar un marco de referencia inercial (uno en el que la Primera Ley de Newton es cierta) con el fin de identificar las fuerzas ejercidas sobre un objeto para que se pueda aplicar la Segunda Ley de Newton. Es posible aplicar las Leyes de Newton en un marco de referencia no inercial, siempre que se incluya una “fuerza inercial” adicional.

Supongamos que colgamos una masa,\(m\), del techo de nuestro auto usando una cuerda. Si el carro acelera hacia adelante con una aceleración constante,\(\vec a\), la masa oscilará hacia la parte trasera del carro y la cuerda no será vertical siempre y cuando el carro mantenga su aceleración constante, como se muestra en la Figura\(\PageIndex{1}\). A medida que el automóvil mantiene su aceleración, la masa colgante no se moverá con relación al automóvil.

Figura\(\PageIndex{1}\): Una masa que cuelga del techo de un automóvil acelerando hacia la derecha.

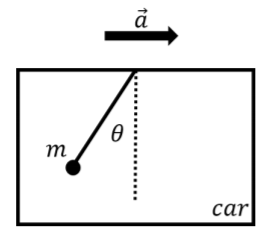
Podemos analizar este movimiento desde el marco inercial de referencia del suelo. En este marco de referencia, hay dos fuerzas ejercidas sobre la masa:

1. \(\vec F_g\), su peso, con magnitud\(mg\).
2. \(\vec T\), una fuerza de tensión ejercida por la cuerda, en la dirección de la cuerda.

Las dos fuerzas se muestran en el diagrama de cuerpo libre de la Figura\(\PageIndex{2}\), junto con un sistema de coordenadas elegido de tal manera que\(x\) apunta en la dirección de la aceleración la masa (que es la misma que la aceleración del automóvil, ya que la masa no se mueve con relación al automóvil).

Figura\(\PageIndex{2}\): Diagrama de cuerpo libre para las fuerzas que actúan sobre una masa suspendida del techo del automóvil acelerador.

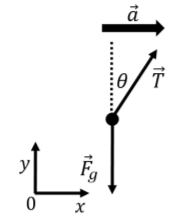
Escribiendo los\(y\) componentes\(x\) y de la Segunda Ley de Newton para la misa, tenemos:\[\begin{aligned} \sum \vec F &= \vec T + \vec F_g= m \vec a\\ \therefore\sum F_x &= T\sin\theta = ma\\ \therefore\sum F_y &= T\cos\theta-F_g=0\end{aligned}\] Podemos, en cambio, modelar el movimiento de la masa en el marco de referencia del automóvil, fingiendo que estamos sentados en el auto. En el marco de referencia del automóvil, la masa es inmóvil, y por lo tanto no tiene aceleración. En el marco no inercial de referencia del automóvil, aún tenemos las fuerzas de peso y tensión ejercidas sobre la masa; estas tienen la misma magnitud y dirección que en el marco inercial de referencia del suelo. Se podría reemplazar la cuerda por una escala de resorte, y los observadores en el automóvil y en el suelo estarían de acuerdo en que la escala de primavera lee el mismo número. Esos observadores también estarían de acuerdo en que el peso de la masa es el mismo. No obstante, los dos observadores no están de acuerdo sobre si la masa se está acelerando, ya que el observador en el automóvil mide que la masa no tiene aceleración.

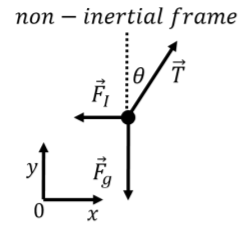
En el marco de referencia del automóvil, la aceleración de la masa es cero. Si queremos que se mantenga la Segunda Ley de Newton, esto implica que, en el marco de referencia del automóvil, la suma de las fuerzas sobre la masa debe ser cero:\[\begin{aligned} \sum \vec F & = 0\quad\quad\text{(car reference frame)}\end{aligned}\] Sabemos por analizar el movimiento del marco de referencia del suelo que la suma vectorial de las fuerzas\(\vec T\) y \(\vec F_g\)es igual a\(m\vec a\). La única manera de que la fuerza en el marco de referencia del automóvil sume a cero es si hay una fuerza adicional,\(\vec F_I\), que se ejerce en ese marco de referencia:\[\begin{aligned} \sum \vec F &= \vec T + \vec F_g + \vec F_I =0\quad\quad\text{(car reference frame)}\end{aligned}\] Como sabemos eso\(\vec T + \vec F_g=m\vec a\), podemos sustituirla en la ecuación anterior:\[\begin{aligned} \sum \vec F &= \vec T + \vec F_g + \vec F_I =0\quad\quad\text{(car reference frame)}\\ &=m\vec a+\vec F_I = 0\\ \therefore F_I &= -m\vec a\end{aligned}\] y nosotros encontrar que esta “fuerza inercial”,\(\vec F_I\), debe ejercerse en sentido contrario a la aceleración del marco de referencia, con una magnitud dada por\(ma\). El diagrama de cuerpo libre para la masa, tal como se ve en el marco de referencia del automóvil, se ilustra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Diagrama de cuerpo libre para las fuerzas que actúan sobre una masa suspendida del techo del automóvil acelerador, en el marco de referencia del automóvil. Una fuerza inercial adicional,\(\vec F_{I} = −m\vec a\), tiene que ser incluida.

Ejemplo\(\PageIndex{1}\)

Estás en un elevador que está acelerando hacia abajo con una aceleración constante\(\vec a\). You are standing on a spring scale. What is the value of your weight as displayed on the spring scale? Assume that your mass is \(m\). (The spring scale will display your weight as having the same magnitude as the normal force that the scale exerts on you).

Solución:

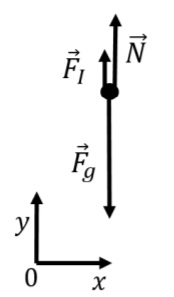
Podemos modelar su movimiento en el marco no inercial de referencia del elevador, donde su aceleración es cero. Las fuerzas que se ejercen sobre ti son:

1. \(\vec F_g\), tu peso, con magnitud\(mg\).
2. \(\vec N\), la fuerza normal ejercida hacia arriba por la báscula de resorte, que es el peso medido por la báscula.
3. \(\vec F_I\), una fuerza inercial con magnitud\(ma\) que se ejerce hacia arriba (en la dirección opuesta a la aceleración del marco de referencia).

Las fuerzas en el marco de referencia del elevador se ilustran en la Figura 5.6.4, junto con un sistema de coordenadas que se eligió para que las fuerzas sean colineales con uno de los ejes (ya que la aceleración es cero).

Figura\(\PageIndex{4}\): Diagrama de cuerpo libre para las fuerzas ejercidas sobre una persona tal como se modelan en un marco de referencia que está acelerando hacia abajo.

Todas las fuerzas están en dirección vertical, por lo que solo necesitamos escribir el\(y\) componente de la Segunda Ley de Newton, que podemos resolver fácilmente para la fuerza normal:\[\begin{aligned} \sum F_y = N+F_I-F_g &=0\\ N + ma -mg &=0\\ \therefore N=m(g-a)\end{aligned}\] Recuerda que debes tener cuidado con los signos. Hemos incluido el hecho de que\(F_I\) se ejerce hacia arriba con el signo más en la primera ecuación (el\(y\) componente de\(\vec F_I=0\hat x+F_I\hat y\) is\(+F_I\)). Luego se utilizó el hecho de que la magnitud de la fuerza inercial viene dada por\(F_I=ma\) en la segunda línea.

Puedes verificar fácilmente que obtendrías el mismo resultado en el marco inercial de referencia del suelo, donde no hay fuerza inercial, pero la aceleración es diferente de cero (y en la\(y\) dirección negativa si usamos el mismo sistema de coordenadas):\[\begin{aligned} \sum F_y =N-mg = -ma \quad\quad\text{(ground frame of reference)}\end{aligned}\] La fuerza normal, que corresponde al peso como se lee por la escala, es así\(N=m(g-a)\). Deberíamos preguntarnos si el resultado tiene sentido:

• Dado que la dimensión de\(a\) y\(g\) son las mismas,\(m(g-a)\) tiene la dimensión correcta de la fuerza.
• Si la aceleración,\(a\), es cero, entonces la magnitud es\(N=mg\), como debería ser si el elevador está en reposo con respecto al suelo.
• Si la aceleración\(a\) es igual a\(g\), la fuerza normal ejercida por la báscula es exactamente cero, y su peso medido es cero. Esto es lo que llamamos ser “ingrávido”, lo que no es una buena descripción, ya que la fuerza de peso todavía se aplica, y es la fuerza normal la que es cero.
• Si la aceleración,\(a\), es mayor que\(g\), entonces la fuerza normal sería negativa. Esto corresponde a que el elevador acelere hacia abajo más rápido que la gravedad, y el modelo se descompone, ya que en este caso, primero golpearía el techo del elevador, que luego ejercería una fuerza normal hacia abajo con magnitud\(m(a+g)\).