6.3: Movimiento circular uniforme

Como vimos en el Capítulo 4, “movimiento circular uniforme” se define como movimiento a lo largo de un círculo con velocidad constante. Este puede ser un buen momento para revisar la Sección 4.4 por la cinemática del movimiento a lo largo de un círculo. En particular, para el movimiento circular uniforme de un objeto alrededor de un círculo de radio\(R\), debe recordar que:

• El vector de velocidad\(\vec v\),, es siempre tangente al círculo.
• El vector de aceleración\(\vec a\),, siempre es perpendicular al vector de velocidad, debido a que la magnitud del vector de velocidad no cambia.
• El vector de aceleración\(\vec a\),, siempre apunta hacia el centro del círculo.
• El vector de aceleración tiene magnitud\(a=v^2/R\).
• La velocidad angular,\(\omega\), está relacionada con la magnitud del vector de velocidad por\(v=\omega R\) y es constante.
• La aceleración angular,\(\alpha\), es cero para el movimiento circular uniforme, ya que la velocidad angular no cambia.

En particular, debe recordar que aunque la velocidad sea constante, el vector de aceleración siempre es distinto de cero en movimiento circular uniforme porque la velocidad cambia de dirección. Según la Segunda Ley de Newton, esto implica que debe haber una fuerza neta sobre el objeto que se dirija hacia el centro del círculo ¹ (paralela a la aceleración):\[\begin{aligned} \sum \vec F = m\vec a\end{aligned}\] donde la aceleración tiene una magnitud\(a=v^2/R\). Debido a que la aceleración se dirige hacia el centro del círculo, a veces la llamamos aceleración “radial” (paralela al radio)\(a_R\), o una aceleración “centrípeta” (dirigida hacia el centro),\(a_c\).

Considere un objeto en movimiento circular uniforme en un plano horizontal sobre una superficie sin fricción, como se representa en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un objeto que experimenta un movimiento circular uniforme sobre una superficie sin fricción, visto desde arriba.

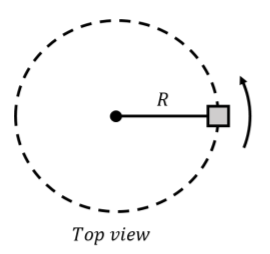
La única manera de que el objeto sufra un movimiento circular uniforme como se representa es si la fuerza neta sobre el objeto se dirige hacia el centro del círculo. Una forma de tener una fuerza que se dirija hacia el centro del círculo es unir una cuerda entre el centro del círculo y el objeto, como se muestra en la Figura\(\PageIndex{1}\). Si la cuerda está bajo tensión, la fuerza de tensión siempre estará hacia el centro del círculo. Las fuerzas sobre el objeto son así:

1. \(\vec F_g\), su peso con magnitud\(mg\).
2. \(\vec N\), una fuerza normal ejercida por la superficie.
3. \(\vec T\), una fuerza de tensión ejercida por la cuerda.

Las fuerzas se representan en el diagrama de cuerpo libre mostrado en la Figura\(\PageIndex{2}\) (visto desde un lado), donde también dibujamos el vector de aceleración. Tenga en cuenta que este diagrama de cuerpo libre solo es “válido” en un instante particular en el tiempo ya que el vector de aceleración cambia continuamente de dirección y no siempre estaría alineado con el\(x\) eje.

Figura\(\PageIndex{2}\) sometida a movimiento circular uniforme.

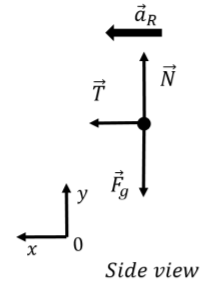
Escribiendo los\(y\) componentes\(x\) y de la Segunda Ley de Newton:\[\begin{aligned} \sum F_x &= T = ma_R\\ \sum F_y &= N - F_g =0\end{aligned}\] El\(y\) componente solo nos dice que la fuerza normal debe tener la misma magnitud que el peso porque el objeto no está acelerando en la dirección vertical. El\(x\) componente nos dice la relación entre las magnitudes de la tensión en la cuerda y la aceleración radial. Usando la velocidad del objeto, también podemos escribir la relación entre la tensión y la velocidad:\[\begin{aligned} T &= ma_R=m\frac{v^2}{R}\\\end{aligned}\] Así, encontramos que la tensión en la cuerda aumenta con el cuadrado de la velocidad, y disminuye con el radio del círculo.

Ejercicio\(\PageIndex{1}\)

Figura\(\PageIndex{3}\): Posibles trayectorias (en rojo) que seguirá el bloque si la cuerda se rompe.

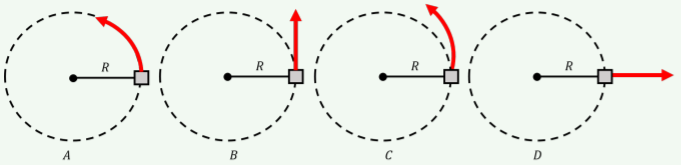
Un objeto está experimentando un movimiento circular uniforme en el plano horizontal, cuando la cuerda que conecta el objeto con el centro de rotación se rompe repentinamente. ¿Qué camino tomará el bloque después de que se rompiera la cuerda?

1. A
2. B
3. C
4. D

Responder

Ejemplo\(\PageIndex{1}\)

Figura\(\PageIndex{4}\): Un automóvil que gira alrededor de una curva que puede aproximarse como el arco de un círculo de radio\(R\).

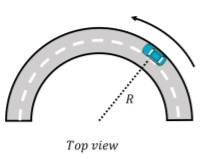
Un automóvil gira alrededor de una curva que puede aproximarse como el arco de un círculo de radio\(R\), como se muestra en la Figura\(\PageIndex{4}\). El coeficiente de fricción estática entre las llantas del automóvil y la carretera es\(µ_{s}\). ¿Cuál es la velocidad máxima con la que el automóvil puede dar la vuelta a la curva sin derrapar?

Solución:

Si el automóvil va a velocidad constante alrededor de un círculo, entonces la suma de las fuerzas sobre el automóvil debe dirigirse hacia el centro del círculo. La única fuerza sobre el automóvil que podría dirigirse hacia el centro del círculo es la fuerza de fricción entre las llantas y la carretera. Si la carretera fuera perfectamente resbaladiza (piense manejando en condiciones heladas), no sería posible circular alrededor de una curva ya que no podría haber fuerza de fricción. Las fuerzas en el auto son:

1. \(\vec F_g\), su peso con magnitud\(mg\).
2. \(\vec N\), una fuerza normal ejercida hacia arriba por la carretera.
3. \(\vec f_s\), una fuerza de fricción estática entre las llantas y la carretera. Esto es fricción estática, debido a que la superficie del neumático no se mueve con relación a la superficie de la carretera si el automóvil no está derrapando. La fuerza de fricción estática tiene una magnitud que es como mucho\(f_s\leq\mu_sN\).

Las fuerzas sobre el automóvil se muestran en el diagrama de cuerpo libre en la Figura 6.3.5.

Figura\(\PageIndex{5}\): Diagrama de carrocería libre para el automóvil visto mirando el auto desde atrás (el centro de la curva está hacia la izquierda).

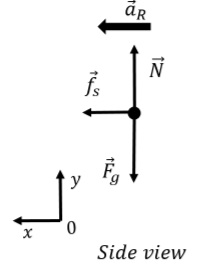
El\(y\) componente de la Segunda Ley de Newton nos dice que la fuerza normal ejercida por la carretera debe ser igual al peso del automóvil:\[\begin{aligned} \sum F_y = N-F_g&=0\\ \therefore N &=mg\end{aligned}\] El\(x\) componente relaciona la fuerza de fricción con la aceleración radial (y así con la velocidad):\[\begin{aligned} \sum F_x = f_s =ma_R&=m\frac{v^2}{R}\\ \therefore f_s &= m\frac{v^2}{R}\end{aligned}\] La fuerza de fricción debe ser menor o igual a\(f_s\leq\mu_sN=\mu_smg\) (ya que a\(N=mg\) partir del\(y\) componente de la Segunda Ley de Newton), lo que nos da una condición sobre la velocidad:\[\begin{aligned} f_s = m\frac{v^2}{R}&\leq\mu_smg\\ v^2 &\leq \mu_s g R\\ \therefore v &\leq \sqrt{\mu_s g R}\end{aligned}\] Así, si la velocidad es menor que\(\sqrt{\mu_s g R}\), el carro no va a patinar y la magnitud de la fuerza de fricción estática, que resulta en una aceleración hacia el centro del círculo, será menor o igual a su valor máximo posible.

Discusión:

El modelo para la velocidad máxima que puede recorrer el automóvil alrededor de la curva tiene sentido porque:

• La dimensión de\(\sqrt{\mu_s g R}\) es la velocidad.
• La velocidad es mayor si el radio de la curva es mayor (uno puede ir más rápido alrededor de una curva más ancha sin derrapar).
• La velocidad es mayor si el coeficiente de fricción es grande (si la fuerza de fricción es mayor, se puede sostener una aceleración radial mayor).

Ejemplo\(\PageIndex{2}\)

Figura\(\PageIndex{6}\): Una bola unida a una cuerda que experimenta movimiento circular en un plano vertical.

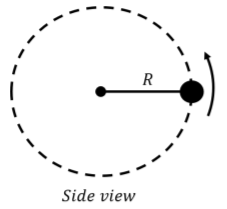
Una bola se une a una cuerda sin masa y ejecuta un movimiento circular a lo largo de un círculo de radio\(R\) that is in the vertical plane, as depicted in Figure \(\PageIndex{6}\). Can the speed of the ball be constant? What is the minimum speed of the ball at the top of the circle if it is able to make it around the circle?

Solución:

Las fuerzas que están actuando sobre el balón son:

1. \(\vec F_g\), su peso con magnitud\(mg\).
2. \(\vec T\), una fuerza de tensión ejercida por la cuerda.

La figura\(\PageIndex{7}\) muestra el diagrama de cuerpo libre para las fuerzas sobre la pelota en tres ubicaciones diferentes a lo largo de la trayectoria del círculo.

Figura\(\PageIndex{7}\): Una bola unida a una cuerda que experimenta movimiento circular en un plano vertical.

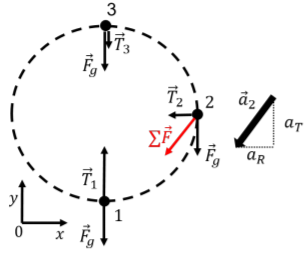
Para que la pelota dé vueltas en círculo, debe haber al menos un componente de la fuerza neta sobre la pelota que esté dirigido hacia el centro del círculo en todo momento. En la mitad inferior del círculo (posiciones 1 y 2), solo la tensión puede tener un componente dirigido hacia el centro del círculo.

Considere en particular la posición etiquetada 2, cuando la cuerda es horizontal y la tensión es igual a\(\vec T_2\). El diagrama de cuerpo libre en la Figura\(\PageIndex{7}\) también muestra la suma vectorial del peso y la tensión en la posición 2 (la flecha roja etiquetada\(\sum \vec F\)), que apunta hacia abajo y hacia la izquierda. Por lo tanto, es claramente imposible que el vector de aceleración apunte hacia el centro del círculo, y la aceleración tendrá componentes que son tanto tangenciales (\(a_T\)) al círculo como radiales (\(a_R\)), como lo muestra el vector\(\vec a_2\) en la Figura \(\PageIndex{7}\).

La componente radial de la aceleración cambiará la dirección del vector de velocidad para que la bola permanezca en el círculo, y la componente tangencial reducirá la magnitud del vector de velocidad. Según nuestro modelo, es así imposible que la pelota dé la vuelta al círculo a velocidad constante, y la velocidad debe disminuir a medida que va de la posición 2 a la posición 3, no importa cómo se tira de la cuerda (puedes convencerte de esto dibujando el diagrama de cuerpo libre en cualquier punto entre los puntos 2 y 3) .

La velocidad mínima para el balón en la parte superior del círculo viene dada por la condición de que la tensión en la cuerda sea cero justo en la parte superior de la trayectoria (posición 3). El balón aún puede dar la vuelta al círculo porque, en la posición 3, la gravedad está hacia el centro del círculo y así puede dar una aceleración que es radial, incluso sin tensión. El\(y\) componente de la Segunda Ley de Newton, en la posición 3 da:\[\begin{aligned} \sum F_y = -F_g &= ma_y\\ \therefore a_y &=-g\end{aligned}\] La magnitud de la aceleración es la aceleración radial, y así se relaciona con la velocidad en la parte superior de la trayectoria:\[\begin{aligned} a_R&=-a_y=g = m\frac{v^2}{R}\\ \therefore v_{min}&=\sqrt{\frac{gR}{m}}\end{aligned}\] que es la velocidad mínima en la parte superior de la trayectoria para que la pelota pueda continuar a lo largo del círculo. La tensión en la cuerda cambiaría a medida que la pelota se mueve alrededor del círculo, y será más alta en la parte inferior de la trayectoria, ya que la tensión tiene que ser mayor que la gravedad para que la fuerza neta en la parte inferior de la trayectoria sea hacia arriba (hacia el centro del círculo).

Discusión:

El modelo para la velocidad mínima de la pelota en la parte superior del círculo tiene sentido porque:

• \(\sqrt{\frac{gR}{m}}\)tiene la dimensión de la velocidad.
• La velocidad mínima es mayor si el círculo tiene un radio mayor (intente esto con una masa unida al final de una cuerda).
• La velocidad mínima es mayor si la masa es mayor (de nuevo, ¡prueba esto en casa!).

Ejercicio\(\PageIndex{2}\)

Considera una bola unida a una cuerda, siendo girada en un círculo vertical (como la que se muestra en la Figura\(\PageIndex{6}\)). If you shortened the string, how would the minimum angular velocity (measured at the top of the trajectory) required for the ball to make it around the circle change?

1. Disminuiría
2. Se quedaría igual
3. Aumentaría

Responder

Curvas bancarizadas

Como vimos en el Ejemplo 6.3.1, existe una velocidad máxima con la que un automóvil puede dar la vuelta a una curva antes de que comience a derrapar. Es posible que hayas notado que las carreteras, especialmente las autopistas, están bancadas donde hay curvas. Los hipódromos para autos que van alrededor de un óvalo (el aburrido tipo de carreras de autos) también tienen curvas banqueadas. Como veremos, esto permite que la velocidad de los vehículos sea mayor al dar la vuelta a la curva; o mejor dicho, hace que las curvas sean más seguras ya que la velocidad a la que patinarían los vehículos es mayor. En el Ejemplo 6.3.1, vimos que fue la fuerza de fricción estática entre las llantas del automóvil y la carretera la que proporcionó la única fuerza con un componente hacia el centro del círculo. La idea de utilizar una curva inclinada es cambiar la dirección de la fuerza normal entre la carretera y las llantas del automóvil para que también tenga un componente en la dirección hacia el centro del círculo.

Consideremos el carro representado en la Figura el\(\PageIndex{8}\) cual se ve desde atrás haciendo un giro a la izquierda alrededor de una curva que está inclinada por un ángulo\(\theta\) con respecto a la horizontal y puede modelarse como un arco a partir de un círculo de radio\(R\).

Figura\(\PageIndex{8}\): Un carro moviéndose hacia la página y dando la vuelta a un bancado curvado para que esté girando hacia la izquierda (el centro del círculo está a la izquierda).

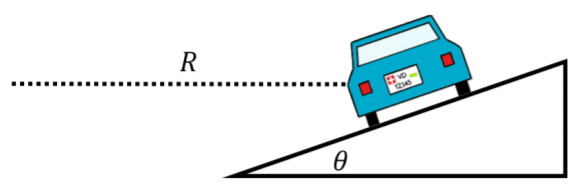
Las fuerzas ejercidas sobre el carro son las mismas que en el Ejemplo 6.3.1, salvo que apuntan en diferentes direcciones. Las fuerzas son:

1. \(\vec F_g\), su peso con magnitud\(mg\).
2. \(\vec N\), una fuerza normal ejercida por la carretera, perpendicular a la superficie de la carretera.
3. \(\vec f_s\), una fuerza de fricción estática entre las llantas y la carretera. Esto es fricción estática, debido a que la superficie del neumático no se mueve con relación a la superficie de la carretera si el automóvil no está derrapando. La fuerza de fricción estática tiene una magnitud que es como mucho\(f_s\leq\mu_sN\) y es perpendicular a la fuerza normal. La fuerza podría ser ya sea hacia arriba o hacia abajo, dependiendo de las otras fuerzas sobre el automóvil.

En la Figura 6.3.9 se muestra un diagrama de cuerpo libre para las fuerzas sobre el automóvil, junto con la aceleración (que está en la dirección radial, hacia el centro del círculo), y nuestra elección del sistema de coordenadas (eligiendo\(x\) paralelo a la aceleración). La dirección de la fuerza de fricción estática no se conoce a priori y depende de la velocidad del automóvil:

• Si la velocidad del automóvil es cero, la fuerza de fricción estática es ascendente. Con una velocidad de cero, la aceleración radial es cero, y la suma de las fuerzas debe ser así cero. El movimiento de impedimento del carro sería deslizarse por la curva inclinada (igual que un bloque en una pendiente).
• Si la velocidad del automóvil es muy grande, la fuerza de fricción estática es hacia abajo, ya que el movimiento que impide el movimiento del automóvil sería deslizarse hacia arriba por el banco. El movimiento natural del automóvil es ir en línea recta (Primera Ley de Newton). Si los componentes de la fuerza normal y de la fuerza de fricción estática dirigida hacia el centro del círculo son demasiado pequeños para permitir que el automóvil gire, entonces el automóvil se deslizaría por el banco (por lo que el movimiento de obstaculización es hacia arriba del banco y la fuerza de fricción estática es hacia abajo).

Figura\(\PageIndex{9}\): Diagrama de cuerpo libre para las fuerzas en el automóvil. No se puede determinar la dirección de la fuerza de fricción estática, ya que depende de la aceleración del automóvil, por lo que se muestra dos veces (con líneas punteadas).

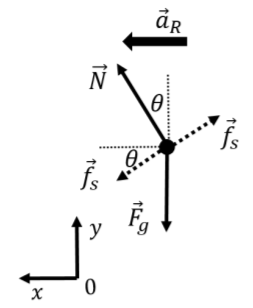
Existe así una “velocidad ideal” a la que la fuerza de fricción estática es precisamente cero, y el\(x\) componente de la fuerza normal es responsable de la aceleración radial. A velocidades más altas, la fuerza de fricción estática es descendente y aumenta en magnitud para mantener la aceleración del automóvil hacia el centro del círculo. A cierta velocidad máxima, la fuerza de fricción alcanzará su valor máximo, y ya no podrá mantener la aceleración del automóvil apuntando hacia el centro del círculo. A velocidades inferiores a la velocidad ideal, la fuerza de fricción se dirige hacia arriba para evitar que el automóvil se deslice por el banco. Si el coeficiente de fricción estática es demasiado bajo, es posible que a bajas velocidades, el automóvil comience a deslizarse por la orilla (por lo que habría una velocidad mínima por debajo de la cual el automóvil comenzaría a deslizarse hacia abajo).

Vamos a modelar la situación en la que la fuerza de fricción estática es idéntica a cero para que podamos determinar la velocidad ideal para la curva bancada. Las únicas dos fuerzas sobre el automóvil son así su peso y la fuerza normal. El\(y\) componente\(x\) y de la Segunda Ley de Newton dan:

\[\begin{aligned} \label{eq:applyingnewtonslaws:carbank_x} \sum F_x &= N\sin\theta = ma_R=m\frac{v^2}{R}\nonumber\end{aligned}\]

\[\therefore N\sin\theta = m\frac{v^{2}}{R}\]

\[\begin{aligned} \label{eq:applyingnewtonslaws:carbank_y} \sum F_y &= N\cos\theta-F_g = 0\nonumber\end{aligned}\]

\[\therefore N\cos\theta =mg\]

Podemos dividir la Ecuación 6.3.1 por la Ecuación 6.3.2\(\tan\theta=\sin\theta/\cos\theta\), señalando que, para obtener:\[\begin{aligned} \tan\theta &= \frac{v^2}{gR}\\ \therefore v_{ideal} &=\sqrt{gR\tan\theta}\end{aligned}\] A esta velocidad, la fuerza de fricción estática es cero. En la práctica, se utilizaría esta ecuación para determinar qué ángulo de inclinación usar al diseñar una carretera, de manera que la velocidad ideal esté alrededor del límite de velocidad o la velocidad promedio del tráfico. Lo dejamos como un ejercicio para determinar la velocidad máxima a la que el auto puede dar la vuelta a la curva antes de deslizarse hacia afuera.

Fuerzas inerciales en movimiento circular

Mientras te sientas en un auto que va dando la vuelta a una curva, te sentirás empujado hacia afuera, lejos del centro del círculo por el que está dando vueltas el auto. Esto se debe a tu inercia (la Primera Ley de Newton), y tu cuerpo iría en línea recta si el auto no te estuviera ejerciendo una fuerza neta hacia el centro del círculo. No estás sintiendo tanto una fuerza que te está empujando hacia afuera como sientes los efectos del asiento del auto empujándote hacia adentro; si estuvieras apoyado contra el costado del auto que está en el exterior de la curva, sentirías el costado del auto empujándote hacia adentro hacia el centro de la curva, incluso si “se siente” como si estuvieras empujando hacia afuera contra el costado del auto.

Si modelamos tu movimiento mirándote desde el suelo, incluiríamos una fuerza de fricción entre el asiento del carro (o el costado del auto, o ambos) y tú que está apuntando hacia el centro del círculo, de manera que la suma de las fuerzas ejercidas sobre ti sea hacia el centro del círculo. También podemos modelar su movimiento desde el marco no inercial del automóvil. Como recordarán, debido a que se trata de un marco de referencia no inercial, necesitamos incluir una fuerza inercial adicional\(\vec F_I\),, que apunta opuesta a la aceleración del automóvil, con magnitud\(F_I=ma_R\) (si la aceleración neta del automóvil es\(a_R\)). Dentro del marco no inercial de referencia del automóvil, su aceleración (relativa al marco de referencia, es decir, el automóvil) es cero. Esto se ilustra mediante los diagramas de la Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\): (Izquierda:) Una persona sentada en un asiento para el automóvil en un automóvil girando hacia la izquierda. (Centro:) Diagrama de cuerpo libre para la persona tal como se modela en el marco de referencia inercial del suelo. (Derecha:) Diagrama de cuerpo libre para la persona modelada en el marco no inercial de referencia del automóvil, incluyendo una fuerza inercial adicional.

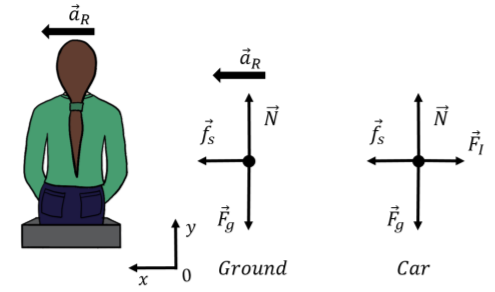
El\(y\) componente de la Segunda Ley de Newton en ambos marcos de referencia es el mismo:\[\begin{aligned} \sum F_y&=N-F_g=0\\ \therefore N&=mg\end{aligned}\] y simplemente nos dice que la fuerza normal es igual al peso. En el marco de referencia del suelo, el\(x\) componente de la Segunda Ley de Newton da:\[\begin{aligned} \sum F_x &= f_s = ma_R\\ \therefore f_s &= m\frac{v^2}{R}\end{aligned}\] En el marco de referencia del automóvil, donde tu aceleración es cero y se ejerce sobre ti una fuerza inercial de magnitud\(F_I=mv^2/R\), el\(x\) componente de Newton da la Segunda Ley:\[\begin{aligned} \sum F_x &= f_s-F_I = 0\\ \therefore f_s - m\frac{v^2}{R} &= 0\end{aligned}\] que por supuesto, matemáticamente, es exactamente equivalente. La fuerza inercial no es una fuerza real en el sentido de que no es ejercida por nada. Sólo entra en juego porque estamos tratando de usar las Leyes de Newton en un marco de referencia no inercial. Sin embargo, sí proporciona un buen modelo para describir la sensación que tenemos de ser empujados hacia afuera cuando el automóvil gira alrededor de una curva. En ocasiones, la gente se referirá a esta fuerza como una fuerza “centrífuga”, que significa “una fuerza que apunta lejos del centro”. Sin embargo, debes recordar que esta no es una fuerza real ejercida sobre el objeto, sino que es el resultado de modelar el movimiento en un marco de referencia no inercial.

Ejercicio\(\PageIndex{3}\)

Jamie está conduciendo su triciclo alrededor de un estanque circular. Jamie siente una fuerza centrífuga con magnitud\(F_I\). If Jamie pedals twice as fast, what will be the magnitude of the centrifugal force that he experiences?

1. \(\sqrt{2}F_I\)
2. \(\frac{1}{2}F_I\)
3. \(2F_I\)
4. \(4F_I\)

Responder

Notas al pie

1. A la suma de las fuerzas se le suele llamar la “fuerza neta” sobre un objeto, y en el caso específico del movimiento circular uniforme, esa fuerza neta se denomina a veces la “fuerza centrípeta”; sin embargo, no es una fuerza en sí misma y siempre es la suma de las fuerzas que apunta hacia el centro del círculo.