6.4: Movimiento circular no uniforme
- Page ID
- 129148
En movimiento circular no uniforme, el movimiento de un objeto es a lo largo de un círculo, pero la velocidad del objeto no es constante. En particular, será cierto lo siguiente
- El vector de velocidad del objeto es siempre tangente al círculo.
- La velocidad y la velocidad angular del objeto no son constantes.
- La aceleración angular del objeto no es cero.
- El vector de aceleración no apuntará hacia el centro del círculo.
Dado que el vector de aceleración no apunta hacia el centro del círculo, generalmente es conveniente descomponer el vector de aceleración en dos componentes:\(a_R\), un componente que es radial (hacia el centro del círculo), y\(a_T\), un componente que es tangente al círculo (y perpendicular a la componente radial). El componente radial es “responsable” del cambio de dirección de la velocidad de tal manera que el objeto va en un círculo. la magnitud de la aceleración radial es la misma que lo es para el movimiento circular uniforme:\[\begin{aligned} a_R=\frac{v^2}{r}\end{aligned}\] donde la velocidad ya no es constante en el tiempo. El componente tangencial de la aceleración es responsable de cambiar la magnitud de la velocidad del objeto:\[\begin{aligned} a_T = \frac{dv}{dt}\end{aligned}\]
Ejemplo\(\PageIndex{1}\)
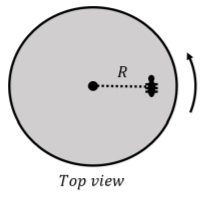
Una hormiga pequeña está durmiendo en un plato giratorio justo cuando el tocadiscos comienza a girar desde el reposo, con una aceleración angular\(\alpha=1\text{rad/s}^{2}\) that is small enough so that, initially, the ant remains on the turntable. The ant is a distance \(R=0.1\text{m}\) from the center of the turntable, as shown in Figure \(\PageIndex{1}\) and the coefficient of static friction between the ant’s “feet” and the turntable is \(\mu_s=0.5\). After how much time will the ant slide off from the turntable?
Solución:
A medida que el plato giratorio se acelera, la fuerza de fricción estática entre el plato giratorio y la hormiga mantendrá a la hormiga en movimiento con el plato giratorio. Una vez que el plato giratorio va lo suficientemente rápido, la fuerza de fricción ya no será lo suficientemente grande como para proporcionar la aceleración total que se requiere para mantener a la hormiga en movimiento con el plato giratorio (con un componente tangencial constante de la aceleración y un componente radial creciente de la aceleración).
Las fuerzas sobre la hormiga son:
- \(\vec F_g\), su peso, con magnitud\(mg\).
- \(\vec N\), una fuerza normal ejercida por el plato giratorio sobre la hormiga.
- \(\vec f_s\), una fuerza de fricción estática ejercida por el plato giratorio sobre la hormiga. La fuerza de fricción será tal que tenga componentes tanto radiales como tangenciales.
Un diagrama de cuerpo libre para las fuerzas sobre la hormiga se muestra en la Figura 6.4.2, visto desde arriba y desde el costado, por algún momento. Hemos elegido el punto en el tiempo para ser justo cuando la hormiga está a punto de deslizarse fuera del plato giratorio, cuando la fuerza de fricción estática hace un ángulo desconocido\(\theta\) con el\(x\) eje. Hemos colocado el origen del sistema de coordenadas en el centro del plato giratorio y elegido el\(x\) eje de tal manera que la hormiga se ubica en el\(x\) eje positivo con su velocidad en la\(y\) dirección positiva. Se utilizó un sistema de coordenadas tridimensionales donde el peso y la fuerza normal se ejercen en la dirección\(z\) (vertical) ya que el vector de aceleración de la hormiga tendrá componentes tanto radiales (\(x\)) como tangenciales (\(y\)).
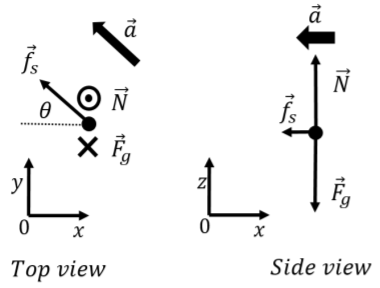
La Segunda Ley de Newton tiene que ser escrita en tres componentes. El\(z\) componente relaciona el peso y la fuerza normal:\[\begin{aligned} \sum F_z &= N - F_g = 0\\ \therefore N&=mg\end{aligned}\] El\(x\) componente de la Segunda Ley de Newton es tal que el\(x\) componente de la aceleración es su componente radial:\[\begin{aligned} \sum F_x &= -f_s\cos\theta = -ma_R = -m\frac{v^2}{R}\\ \therefore f_s\cos\theta &= m\frac{v^2}{R}\end{aligned}\] El\(y\) componente de la Segunda Ley de Newton relaciona el componente tangencial de la fuerza de fricción estática con el componente tangencial de la aceleración:\[\begin{aligned} \sum F_y &= f_s\sin\theta = ma_T \\ \therefore f_s\sin\theta &= m\alpha R\end{aligned}\] donde se utilizó el hecho de que la aceleración tangencial (lineal)\(a_T\), está relacionada con la aceleración angular,\(\alpha\), por:\[\begin{aligned} a_T = \alpha R\end{aligned}\] Resumiendo las tres ecuaciones que obtuvimos de los tres componentes de la Segunda Ley de Newton:\[\begin{aligned} f_s\cos\theta &= m\frac{v^2}{R}\\ f_s\sin\theta &= m\alpha R\\ N&=mg\end{aligned}\] También, tenga en cuenta que la velocidad,\(v(t)\) en algún momento\(t\) viene dada por la cinemática simple:\[\begin{aligned} v(t)=v_0+a_Tt=(0)+\alpha R t\end{aligned}\] La hormiga comenzará a deslizarse cuando la fuerza de fricción alcance su amplitud máxima,\(f_s=\mu_sN=\mu_Smg\). La Segunda Ley\(x\) de Newton se puede utilizar para encontrar una expresión para el momento en que la fuerza de fricción alcanza su valor máximo (en términos del ángulo desconocido\(\theta\)):\[\begin{aligned} f_s\cos\theta &= m\frac{v^2}{R}\\ \mu_sg\cos\theta &= R\alpha^2t^2\\ \therefore t &= \sqrt{\frac{\mu_sg\cos\theta}{R\alpha^2}}\end{aligned}\] Podemos usar el\(y\) componente para determinar el ángulo
\(\theta\):\[\begin{aligned} f_s\sin\theta &= m\alpha R\\ \mu_sg\sin\theta &= \alpha R\\ \therefore \sin\theta &= \frac{\alpha R}{\mu_s g}\\ \therefore \theta &= \sin^{-1}\left( \frac{\alpha R}{\mu_s g} \right)=\sin^{-1}\left( \frac{(1\text{rad/s}^{2})(0.1\text{m})}{(0.5)(9.8\text{N/kg})} \right)\\ &=1.17^{\cdot}\end{aligned}\]
El ángulo es muy pequeño, y vemos que la fuerza de fricción se dirige principalmente hacia el centro del círculo. La aceleración radial es así mucho mayor que la aceleración tangencial. Entonces podemos usar el ángulo para encontrar el tiempo usando la expresión que derivamos anteriormente:
\[\begin{aligned} t &= \sqrt{\frac{\mu_sg\cos\theta}{R\alpha^2}}= \sqrt{\frac{(0.5)(9.8\text{N/kg})\cos(1.17^{\cdot})}{(0.1\text{m})(1\text{rad/s}^{2})^2}}\\ &=7.0\text{s}\end{aligned}\]


