8: Energía Potencial y Conservación de la Energía
- Page ID
- 129561
En este capítulo, seguimos desarrollando el concepto de energía con el fin de introducir una formulación diferente para la Física Clásica que no utilice fuerzas. Aunque podemos describir muchos fenómenos usando energía en lugar de fuerzas, este método es completamente equivalente a usar las Tres Leyes de Newton. Como tal, este método puede derivarse de la formulación de Newton, como veremos. Debido a que la energía es una cantidad escalar, para muchos problemas, conduce a modelos que son mucho más fáciles de desarrollar matemáticamente que si se hubieran usado fuerzas. El capítulo concluirá con una presentación del enfoque más moderno, utilizando “Mecánica Lagrangiana”, que actualmente se prefiere en la física y forma la base para extender nuestra descripción de la física al mundo microscópico (por ejemplo, la mecánica cuántica).
Objetivos de aprendizaje
- Comprender la diferencia entre fuerzas conservadoras y no conservadoras.
- Entender cómo definir la energía potencial para una fuerza conservadora.
- Entender cómo utilizar la energía potencial para calcular el trabajo.
- Entender la definición de energía mecánica.
- Entender cómo utilizar la conservación de la energía mecánica.
- Entender cómo aplicar la formulación lagrangiana en un caso sencillo.
preludio
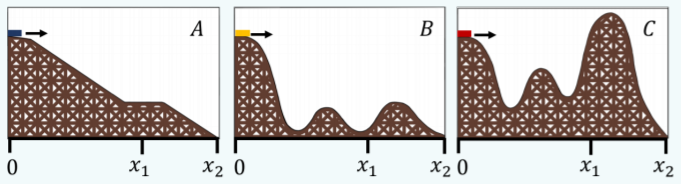
Tres carros de montaña rusa comienzan en la posición\(x = 0\), donde todos están a la misma altura (Figura 8.1). Todos los carros empiezan con la misma velocidad. En\(x_{1}\), ¿qué carro de montaña rusa se moverá más rápido?
Todas las montañas rusas terminan a nivel del suelo, en\(x_{2}\). ¿En qué carro de montaña rusa se moverá más rápido\(x_{2}\)? ¿Todos ellos llegarán a\(x_{2}\)? ¿Quién va a llegar primero? Supongamos que la pista de la montaña rusa no tiene fricción.
Miniatura: Montaña rusa “Blue Fire” en Europa Park. (CC SA 3.0; Posavasos J).


